Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

90 Ulrik Brandes and Gabi Dorfm¨uller

Besides many straightforward criteria such as the location of query terms

in the page (in headlines? near each other?) and many unknown heuristic

rules, a central element of the ranking strategy is an evaluation of the Web’s

linking structure. This component is known as PageRank and is explained in

this chapter.

Tourist Trails

Explanations of PageRank often use for motivation the idea that a page should

be ranked as more relevant, the more frequently one would reach it on a

random walk through the Web. We will explore this idea further, but with a

completely diﬀerent example.

Imagine that, in the 18th century, mathematician Leonhard Euler had not

proven the inexistence of, but rather found the long-sought tour crossing the

seven bridges of K¨onigsberg (cf. Chap. 28). This tour would be famous: It

would be listed in all city guides, and tourists would walk the tour in droves.

Of course, there would also be vendors selling souvenirs and refreshments in

places that these tourists most frequently stroll by – but where are these

places?

For a tour it does not matter where it is begun. Since, however, every bridge

is crossed exactly once, we can at least be sure that every part is visited half

as often as there are bridges leading there: One bridge is needed to get there,

and another one to leave. The most promising selling spots are where the most

bridges converge. In K¨onigsberg, this would be Kneiphof (labeled A).

Alas, there is no such tour. So let’s assume tourists are wandering around

with no particular goal or destination. More concretely, let them choose the

next bridge to cross randomly and with equal probabilities (this is called

“uniformly at random”) from all those that are feasible, including the one

they just came across. How often do they arrive in a certain location?

The number b of visits at, say, node B can be described in terms of the

number of immediately preceding visits at nodes that are connected to B,

here A and D. If the next bridge to continue with is chosen uniformly at

random from all feasible bridges, we get from A to B in two out of ﬁve cases,

10 PageRank – What Is Really Relevant in the World-Wide Web? 91

and from D to B in one out of three. The unknown b can therefore be written

in terms of equally unknown visiting numbers a and d:

b =

a +

Corresponding equations can be given for all the unknowns:

a =

b +

c +

d, c =

a +

d, d =

a +

Interestingly, every solution to this system of equations is of the form a =5

and b = c = d = 3 or multiples thereof; the relative sizes of these numbers

are thus exactly the same as those we would have obtained had there been an

Eulerian tour! Whether tourists are exploring K¨onigsberg systematically or at

random is therefore of no relevance for our vendors. Moreover, this principle

applies to every other city as well, independent of its particular pattern of

connections among bridges.

Trails on the Web

If we interpret hyperlinks as a recommendation to consult the destination Web

page for further information, we can ask the same question that has just been

considered for locations in K¨onigsberg. Which pages does a random surfer,

someone who is not searching for something in particular and is following

links uniformly at random, visit most frequently? It would seem that the

answer depends on the respective number of links entering a page, as it did

for bridges.

In contrast to the bridges of K¨onigsberg, though, links on the Web are like

one-way streets, because they can only be followed in one direction. Note that

we are ignoring the “back” button for the moment. The following example

illustrates that this simple modiﬁcation complicates matters signiﬁcantly.

a = b,

b =

c + d,

c = a,

d =

All arguments for setting up a system of equations for the unknown relative

numbers of visits are still valid, but the solutions of the equation in this par-

ticular example are multiples of a = b = c =2andd = 1. The correspondence

between these numbers and the number of incoming and outgoing links is lost

92 Ulrik Brandes and Gabi Dorfm¨uller

(for otherwise, a would have to equal d and both must be diﬀerent from b

and c).

Real networks in general exhibit at least one other problem in addition to

one-way streets, namely dead ends. In the network depicted here,

one is stuck after following the red link. While simple cases like this one are

easily identiﬁed (and Google is likely to remove them), dead ends can also be

less obvious. In larger networks one might be able to continue from nodes such

as F, but still not be able to return to nodes A,...,E. Pages that eventually

cannot be reached any more lead to solutions of the system of equations that

are not useful for ranking purposes.

The Web-surﬁng behavior mimicked so far, however, is a poor match. If

no, or no interesting, link is found on a page, the next page will be chosen by

other means such as the back button, a bookmark, or direct entry of a new

Web address.

Including such spontaneous jumps to other pages into the model yields a

system of equations that is only a little more complicated. We simply assume

that, for instance, on every ﬁfth occasion the new node was not found by

selecting a link, but directly by some other means. We also assume that there

is no bias toward any of the six pages, i.e., in the long run, each node is equally

often the destination of a jump. This way, every page can be reached at any

point in time, and there are no dead ends.

a =

· b +

b =



· c +1· d + e



c =

· a +

d =



· c



e =

· 0+

f =



· c



This system of equations is only a little more involved and just as easy to

solve as the system in the previous section. Try to determine whether results

from the following experiment resemble a solution!

10 PageRank – What Is Really Relevant in the World-Wide Web? 93

Experiment (10 or more subjects, e.g., your class at school)

Every person starts from any of the pages in the above network and starts

moving through the network by following links at random. If necessary, or

out of the blue, any page can be chosen. After one minute everyone stops

upon a signal and remembers the last page visited. For each page, the number

of subjects that have stopped there is recorded.

A less contrived and somewhat larger example of links between entities is

the present book itself. If chapters are viewed as reading locations, referrals

can be interpreted as links between them.

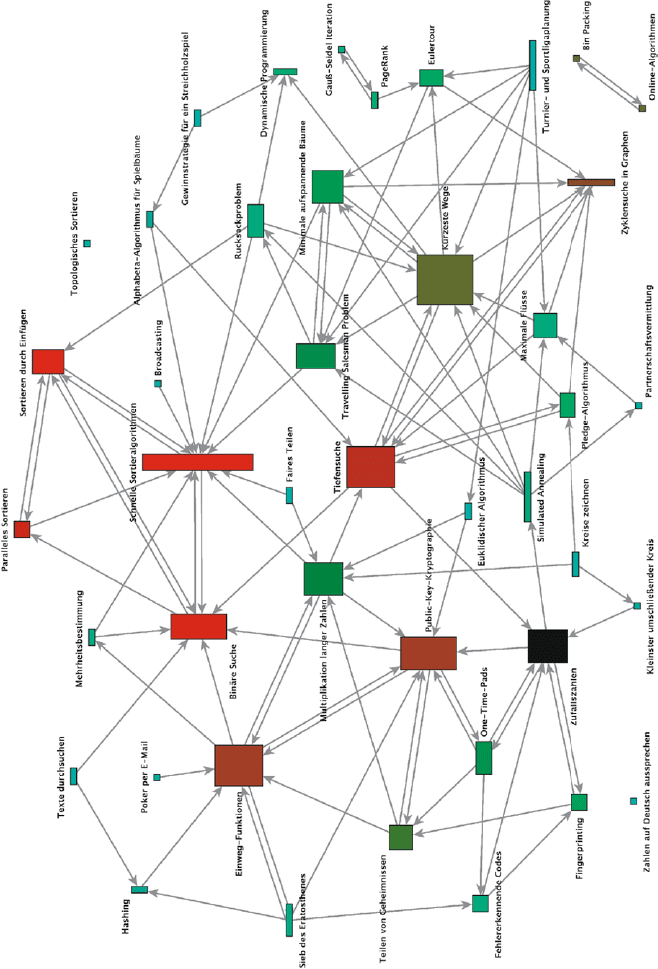
In the network diagram depicted on the next page every chapter in this

book is represented by a rectangle, and their width and height is determined

by the number of links to and from other chapters. A slim, tall rectangle thus

represents a chapter that refers to few others, but is referred to often. Colors

are computed from the equation system and therefore indicate the PageRank

in the referral network: Turquoise rectangles represent chapters with lowest

PageRank, orange rectangles those with highest PageRank, and appropriately

mixed colors are used for values in between.

The chapters on variants of sorting are indeed the ones that a reader ends

up being referred to most often when reading in random fashion, following

links as if on the Web. This matches their crucial role in algorithmics.

Solutions

The model described above cannot be used directly to compare the relevance

of hits returned for a query, since the network that is to be evaluated by an

Internet search engine yields a system with billions of equations. Even the

fastest computers cannot solve such systems using the methods we learn in

school.

Fortunately, the systems resulting from our approach exhibit some special

properties that can be exploited in the search for a solution. Moreover, we do

not really need an exact solution, so that a very simple and eﬃcient algorithm

can instead be used to quickly approximate a solution. There is one equation

for every variable, and if we know the values of all other variables, we would

simply substitute them and thus determine the value of the ﬁnal variable. The

algorithm therefore starts with an arbitrary initial assignment (e.g., the same

non-zero value for all variables) and solves for every variable of the associated

equation relative to the values currently assigned for all other variables. With

these newly obtained assignments the process is repeated, then repeated, and

repeated, and so on.

94 Ulrik Brandes and Gabi Dorfm¨uller

10 PageRank – What Is Really Relevant in the World-Wide Web? 95

PageRank Algorithm (almost)

1 Initialize relevance scores of all pages to 1

2 While scores are changing notably

3 Determine for every page P:

4 set new relevance score for P to



for all pages Q

linking Q → P

relevance of Q

number of links of Q

number of pages

For our six-node example, this yields the following computation (values

rounded to the 5th decimal):

Start 1st step 2nd step . . . 11th step 12th step . . . Solution

a 1.00000 0.83333 0.29467 . . . 0.10758 0.10740 . . . 0.10665

b 1.00000 0.32667 0.28222 . . . 0.09259 0.09241 . . . 0.09164

c 1.00000 0.83333 0.70000 . . . 0.12154 0.11940 . . . 0.11865

d 1.00000 0.30000 0.25556 . . . 0.06592 0.06574 . . . 0.06497

e 1.00000 0.03333 0.03333 . . . 0.03333 0.03333 . . . 0.03333

f 1.00000 0.30000 0.25556 . . . 0.06592 0.06574 . . . 0.06497

The scores are improving with every step, and when they are not changing

by much anymore, this is an indication that we are close to the exact solution.

A detailed explanation for this welcome behavior is given in Chap. 30.

Conclusion

At the end of this chapter the following question should be easy to answer.

Quiz: If you let many of your friends link to your personal homepage, will it

turn out on top of Google’s result list?

Answer:

This is only going to work if your friends’ pages are of high rele-

vance themselves – unlikely to be the case.

Many other ways of scoring linked entities are studied in an exciting area

of research called network analysis. Moreover, there are many ways in which

these structural scores can be utilized in the ﬁnal relevance ranking. A change

in the slightest detail can have a signiﬁcant eﬀect on the results. For example,

we could alter the ratio of jumps and link traversal, or introduce a bias into the

selection of destinations for jumps. The speciﬁc instantiation of the algorithm

and many more details of the relevance ranking are, of course, proprietary

knowledge, but it seems that the decisions made at Google are working not

too badly.

96 Ulrik Brandes and Gabi Dorfm¨uller

Further Reading

1. Chapter 30 (Gauß–Seidel Iterative Method for the Computation of Phys-

ical Problems)

More detailed explanation of how and when systems of linear equations

can be solved by iteratively solving single equations.

2. Chapter 28 (Eulerian Circuits)

There are no Eulerian tours in K¨onigsberg, but there are where Santa

dwells.

3. Wikipedia article

http://en.wikipedia.org/wiki/PageRank

More abstract formulation, background information and more references.

Part II

Arithmetic and Encryption

Overview

Berthold V¨ocking

RWTH Aachen, Aachen, Germany

Even in the very ﬁrst years of school we were confronted with algorithms for

basic arithmetic. We were taught how to add multidigit numbers by writing

the numbers below each other and then adding digit by digit, carrying an

overﬂow digit from right to left. Based on this algorithm for addition, we then

learned an algorithm for multiplication. Two multidigit numbers are multi-

plied by ﬁrst multiplying the multiplicand by each digit of the multiplier and

then adding up all the properly shifted results. These grade-school algorithms

follow simple rules and can thus be executed using a calculator or a computer

which typically, however, use binary rather than decimal digits. In fact, every

pocket calculator does these calculations much faster and more reliably than

humans and, thus, we are no longer accustomed to performing them by hand.

This part of the book starts with algorithms for diﬀerent kinds of arith-

metic problems. In Chap. 11, an algorithm for fast multiplication is presented

that is much more eﬃcient than the grade school method, especially if one

wants to multiply large numbers consisting of many digits. Chapter 12 deals

with the Euclidean Algorithm for calculating the greatest common divisor of

two given numbers in a very clever and elegant way. This algorithm was known

already in the ancient world and is still used today in diﬀerent variants. In

ancient times, it was even known how to calculate prime numbers. Chapter 13

explains the Sieve of Eratosthenes, a very old but still practical algorithm for

computing a table with all prime numbers up to a speciﬁed number.

Cryptography deals with the encryption and decryption of information.

Chapters 15 and 16 present two diﬀerent cryptographic approaches. Chap-

ter 15 presents the so-called One-Time-Pad. This simple symmetric algorithm

uses the same secret key for encryption and decryption. A text can be en-

crypted and decrypted only by someone who knows the secret key. Chapter 16

presents an asymmetric method that uses diﬀerent keys for encryption and

decryption. The key for encryption is announced publically so that everybody

can encode a message. Only the owner of the matching secret key can de-

code the encrypted message. Most cryptographic schemes used today in the

Internet are based on asymmetric algorithms using a secret and a public key.

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0,

 Springer-Verlag Berlin Heidelberg 2011