Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

40 Hagen H¨opfner

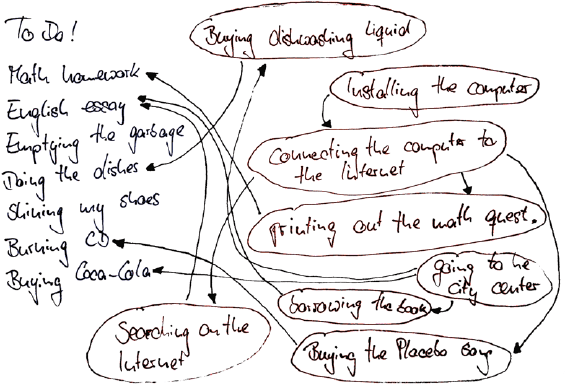
Well, it is certainly not possible to complete the tasks on my To Do list

in the order they are written. The point is that I can’t burn a CD with-

out having all the songs, and in order to get all songs I have to install the

computer and to connect it to the Internet ﬁrst. Hence, there are some de-

pendencies among the diﬀerent tasks, and not all subtasks have been listed

so far. That is why I now pick up my pen and complete my To Do list. Be-

fore doing the dishes I have to buy dishwashing liquid. Therefore, I draw

an arrow from “buying dishwashing liquid” to “doing the dishes.” In order

to buy the dishwashing liquid I have to go to the city center. So, I draw

an arrow from “going to the city center” to “buying dishwashing liquid,”

etc.

Wow, this is much worse than I thought! Where shall I start? This makes

me aware that I have to do a lot. Anyway, the question remains: how shall

I start oﬀ with the stuﬀ? An arrow shows me that I have to do something

before I can work on something else. Hence, I can only fulﬁll a task when no

arrowspointtoit.

Very well then! I can only start with something that has no incoming

arrows. Thus, I have only the following choices:

• emptying the garbage

• shining my shoes

• installing the computer

• going to the city center

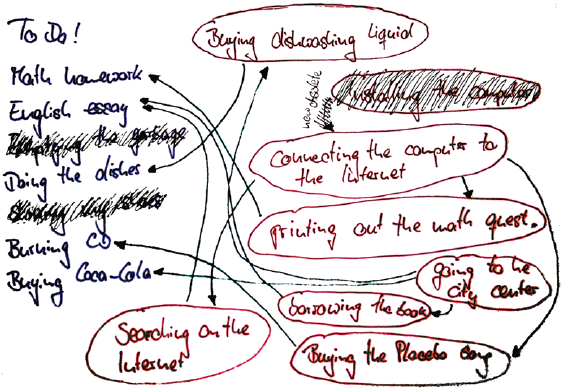
Actually it doesn’t make any diﬀerence which of these four alternatives

I choose. Well, I am a nice guy, and therefore ﬁrst I empty the garbage.

5 Topological Sorting 41

Afterwards I’ll shine my shoes before I install the computer. Following this

I can update my To Do overview and remove the tasks I have done. At the

same time, I can also remove the arrows that start at ﬁnished tasks (e.g.

the arrow from “installing the computer” to “connecting the computer to the

Internet”).

Obviously, if I had used a pencil, the updated To Do overview would

be clearer. Then I would have been able to erase the ﬁnished tasks and

the canceled arrows. Never mind! The computer is running and I can draw

an electronic task list, by simply using a graphic software. This reminds

me that computer scientists like my brother call such a To Do list with

sub-tasks and arrows a graph. The tasks are represented by nodes of the

graph, and the dependencies are represented as directed edges between

the nodes. Here “directed” means that the direction of the arrow deﬁnes

the direction of reading the dependency. If it is possible to come back to

the starting point while tracing (without removing the pen) such a graph,

then the graph is a cyclic graph – in other words there is a cycle in the

graph.

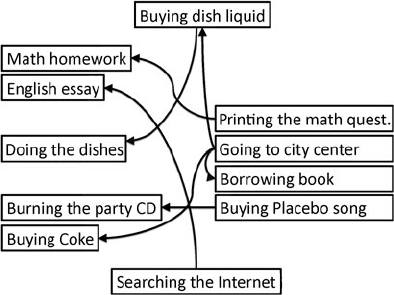
However, what shall I do next? Well, I could still go to the city center. As

I have installed the computer already, I could also connect it to the Internet.

In the end I removed the dependency arrow that pointed to “connecting the

computer to the Internet”. But, all other tasks are still blocked. Since I am

working at the computer at the moment anyway, I can bring it online right

now. Thus, my To Do graph changes again.

42 Hagen H¨opfner

Subsequently I could still go to the city center, search online for the infor-

mation that I need for my English essay, buy the Placebo song or print out

my math questionnaire.

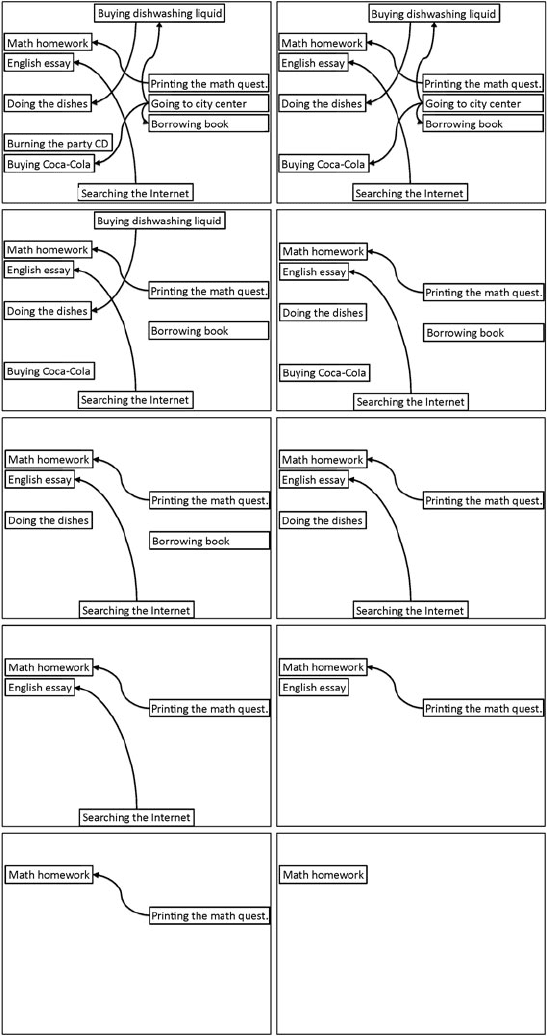
Done! In a few minutes I’ll go to the party. Let me shortly summarize the

order in which I ﬁnished my To Do list today:

1. emptying the garbage

2. shining my shoes

3. installing the computer

4. connecting the computer to the Internet

5. buying the Placebo song

6. burning the party CD

7. going to the city center

8. buying the dishwashing liquid

9. buying Coca-Cola

10. borrowing the book from the library

11. doing the dishes

12. searching for information on the Internet

13. writing the English essay

14. printing out the math questionnaire

15. answering the math questionnaire

After ﬁnishing a subtask, I always removed the entry and all arrows start-

ing at this entry from my To Do graph. Hence, step by step I removed all nodes

from the graph and saved the chosen sequence. You can read the results from

top left to bottom right.

5 Topological Sorting 43

44 Hagen H¨opfner

My big brother, who is studying computer science, told me a few min-

utes ago that I used topological sorting. He gave me the following algorithm

description:

The TopSort algorithm outputs the nodes of a directed graph in a topo-

logical order. At this, the graph G =(V,E) consists of the set of nodes V

and a set of edges E of the form (node1,node2), whereas the dependency is

directed from node1tonode2andV must contain both nodes.

1 function TopSort

2 while V is not empty do

3 cycle:=true

4 for each v in V do

5 if there is an edge e in E of the form (X, v) then

// X is an arbitrary other node

6removev from V

7 remove all edges of the form (v, X)fromE

8 cycle:=false

9 print v // printing out the nodes

10 endif

11 endfor

12 if cycle=true then

13 print I cannot resolve cyclic dependencies!

14 break // abort while loop

15 endif

16 endwhile

17 end

Moreover, the algorithm detects cyclic graphs that cannot be sorted topo-

logically. This is done by checking whether or not each step removes one node.

In the case that no node is removed before reaching an empty graph, the al-

gorithm automatically stops.

Furthermore, the example used above illustrates a general computer prob-

lem. Computers do their jobs in a “stupid” way, step by step. TopSort aims

at ﬁnding one possible topological order. Such a correct topological order

would also be:

• ...

• going to the city center

• buying dishwashing liquid

• doing the dishes

• ...

• buying Coca-Cola

• ...

In this case we would have gone to the city center but would not have

done all necessary shopping. The problem would be, though, that we would

have to go to the city center again in order to buy Coca-Cola. However, this

5 Topological Sorting 45

information has already been removed from the graph. Hence, a little bit of

organizing ability is still required to plan the daily routine.

Further Applications

Topological sorting ﬁnds an order that respects the direction of the edges.

This happens independently of the situation represented by the graph and

its nodes because the algorithm does not need to take this into account. The

algorithm simply removes incoming and outgoing edges one by one. Therefore,

it can be used in various areas of computer science. For example, it can help

us to detect deadlocks that might result from parallel access to resources: If

a program wants to exclusively use a resource (e.g., a ﬁle) in a computer, the

resource gets locked and cannot be used by other programs. These programs

must wait until the lock is released. A deadlock happens if a program that

waits for a resource locks another resource that is being used by the ﬁrst

program. Hence, both programs wait for each other and neither of them can

ﬁnish its task. It is possible to represent such a wait-for relationship in a wait-

for graph. A deadlock leads to a cycle in the graph and can be detected using

TopSort. In the end, one program participating in the deadlock must be

aborted.

Additional Reading

1. From Wikipedia:

http://en.wikipedia.org/wiki/Topological

sorting

SearchingTexts–ButFast!

The Boyer–Moore–Horspool Algorithm

Markus E. Nebel

TU Kaiserslautern, Kaiserslautern, Germany

Within a computer’s memory many objects to be processed are represented

in the form of text. A straightforward example is text generated by a word

processing program. However, documents published on the Internet are usu-

ally hosted by a Web server in the form of so-called HTML documents, i.e.,

as text with integrated formatting instructions, links to image ﬁles, etc. In

this chapter we will focus on the search of words within text. Why? Sim-

ply because of the many situations in which this problem is at hand. Imag-

ine that we performed a Web search using Google and found a Web site

with plenty pages of text. Of course, we want to know where in the text

our search word can be found and we want our Web browser to perform

the task of highlighting all the corresponding positions in the text. Accord-

ingly, the browser needs a routine which ﬁnds all those occurrences as fast

as possible. It should be obvious that we face the same or similar demands

quite often. Therefore, we will deal with the so-called string matching prob-

lem, i.e., the problem of searching for all occurrences of a word w within a

text t.

The Naive Algorithm

Within a computer, texts are stored symbol by symbol (letter by letter).

Accordingly, it is not possible to compare a word w with a part of a text in

a single step. In order to decide whether w occurs at a speciﬁc position we

need to compare the text and w symbol by symbol. Assuming text t to consist

of n symbols, we will denote by t[i], i an integer between 1 and n,thenth

symbol of t.Thust[1] denotes the ﬁrst, t[2] the second symbol, and so on.

Finally, t[n] represents the last symbol of the text. We will make use of the

same notation for the symbols of w, assuming its length to be given by m.

Then, when writing w[j] to represent the jth symbol of word w, j must be

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0

 Springer-Verlag Berlin Heidelberg 2011

48 Markus E. Nebel

an integer between 1 and m. As an example consider the text Haystack with

a needle in which we are searching for the word needle. In this case t and w

look like the following (a column headed by number k contains the symbol

t[k]orw[k]):

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

a y s t a c k w i t h a n e e d l e

1 2 3 4 5 6

n e e d l e

In our example, we have n =22andm =6,andt[1] = H, t[2] = a,and

w[4] = d. Please note that spaces of the text have to be considered as symbols

too, and cannot be ignored. In the sequel, we will use this text as our running

example.

In order to decide whether this text starts with the word w = needle,an

algorithm must compare the beginning of t and w symbol by symbol. If all

symbols match, we report success and the ﬁrst occurrence of w is located at

the ﬁrst position of t. Obviously this is not the case for our example. In order

to determine that, it is suﬃcient to compare t[1] with w[1], which yields a

mismatch; t[1] = H = w[1] = n. By this mismatch our program concludes that

w does not occur at the ﬁrst position of t.Onlyifallm comparisons of the

symbols of w to the corresponding symbols of t provide a match is w for sure

contained in t. In our case, a single comparison is suﬃcient to observe the

contrary, but obviously this is not the case in general. For example, consider

the search of w = Hayrack within t. In this case, even if w does not occur at

theﬁrstpositionoft, the ﬁrst three comparisons provide a match and we have

to wait until the fourth comparison of w[4] to t[4] to determine a diﬀerence;

s is diﬀerent from r.

The following short program successively executes the comparisons just

discussed. Contrary to our examples it starts with the last symbol of w instead

of the ﬁrst in order to compare w to a part of t from right to left. The reason

for this will become clear later.

Comparing word w and text t at ﬁrst position symbol by symbol

1 j := m;

2 while (j>0) and (w[j]=t[j]) do

3 j := j − 1;

4 if (j =0)then print(“Occurrence at position 1”);

6 Searching Texts – But Fast! 49

1 2 3 4 5 6 7 8 ...

H a y s t a c k

 j=m=4

d a y s

↓ j:=j−1

H a y s t a c k

 j=3

d a y s

↓ j:=j−1

a y s t a c k

 j=2

d a y s

↓ j:=j−1

a y s t a c k

| j=1

a y s

The ﬁgure to the left clariﬁes the

function of this little program when

searching text t from above for w =

days. Here, a green double arrow

represents a comparison of two iden-

tical symbols; a read bar connects

two symbols for which a mismatch

has been observed. Beginning with

w[4], the text is compared symbol by

symbol to w until either j becomes 0

(which is not the case in our exam-

ple, and would imply an occurrence

of w as part of the text) or the sym-

bols w[j]andt[j] just compared do

not match (which happens for j =1

in our example). These two condi-

tions are checked within the while-

loop of the program.

In general,

while (j>0) and (w[j]=t[j])doj := j − 1;

means that j is decreased by 1 as long as it is larger than 0 and the jth symbol

of the text is equal to the jth symbol of the word. Thus, in cases where the

ﬁrst m symbols of the text do not match w, the second condition eventually

gets violated, leaving a value of j larger than 0. As a consequence, in line 4

of our program the command if (j =0) ... will not report an occurrence

(printing the text “Occurrence at position 1” is only a surrogate for any action

to be taken in case of an occurrence of w). If, on the contrary, all m symbols of

w match the ﬁrst m symbols of t, then the while-loop terminates since j =0

holds. In this case our program reports success.

Since we have to ﬁnd all occurrences of w as a substring of t,weobvi-

ously have to search other locations of t than just the beginning. In fact, w

may start at any position of t which has to be checked by our program. In

this

context, an

y position of t means that we have to expect an occurrence

of w at the second, third, . . . positions of t also. For the second position

we must decide if w[1] = t[2] and w[2] = t[3] and ... and w[m]=t[m +1]

hold. The third, fourth, . . . positions have to be examined analogously; the

(n − m + 1)th position is the last to be considered where w[m]andt[n]are

aligned. Considering position pos,wehavetocomparew[1] and t[pos], w[2] and

t[pos +1],...,w[m]andt[pos + m −1] (which our algorithm will do in reverse

order). By introducing an additional variable pos we can easily extend our

program to (according to our preliminary considerations) search for w at any

position of t (parts of the program adopted from above are printed in blue).