Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

20 Helmut Alt

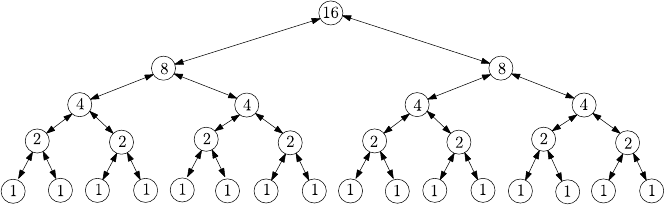
Fig. 3.1. Recursion tree for Mergesort

The descriptions in the previous section show that a computer is not neces-

sarily needed for the execution of the algorithms. For a better understanding of

both algorithms we recommend that you carry them out “by hand” adopting

the roles of the various “helpers” yourself.

In all high-level programming languages (e.g., C, C++, Java) it is possible

for a procedure to call “itself” to solve the same task in the same manner

for a smaller subproblem. This concept is called recursion and it plays an

important role in computer science. For example, if you apply Mergesort to

a sequence of 16 numbers, then both helpers get a subsequence of length 8

each to be sorted. Each of them again calls his two helpers to sort sequences

of length 4, and so on. The complete operation of this algorithm is presented

in Fig. 3.1, which is called a tree in computer science.

The recursion stops when the subproblems become suﬃciently small to be

solved directly. In our algorithms this is the case for sequences of length 1,

where nothing has to be done any more to have them sorted. In both de-

scriptions of the algorithms, statement 1 takes care of this base case of the

recursion.

So, our algorithms solve a large problem by decomposing it into smaller

subproblems, solving those recursively, and combining the resulting partial

solutions for a complete solution. Proceeding in this manner is called divide-

and-conquer in computer science. This principle can be applied successfully

not only to sorting but also to many other, quite diﬀerent problems.

3.3 Experimental Comparison of the Sorting Algorithms

It is a natural question as to why algorithms that strange should be used

for sorting, which seems to be a really simple problem. Therefore, we imple-

mented (i.e., programmed) both algorithms, as well as Sorting by insertion

from Chap. 2, on a computer at our institute and recorded the time that

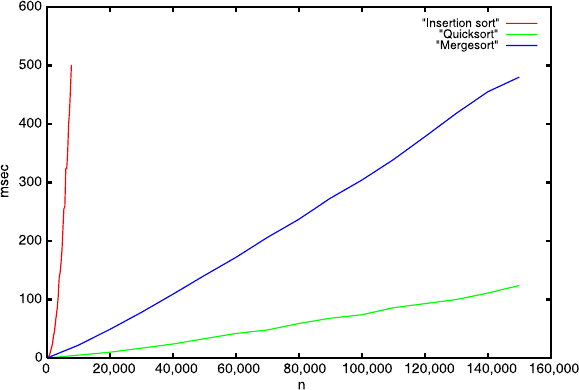
those algorithms needed for sequences of numbers of diﬀerent lengths. Fig-

ure 3.2 shows the result. Obviously, Mergesort is much faster than Sorting by

insertion and Quicksort is signiﬁcantly faster than Mergesort.

3 Fast Sorting Algorithms 21

Fig. 3.2. Runtimes in milliseconds of the three algorithms determined experimen-

tally for sorting sequences of lengths 1 to 150,000

In half a second (500 ms) of computation time, Sorting by insertion can

sort sequences of length up to 8,000, whereas Mergesort manages 20 times as

many numbers in the same time. Quicksort is four times faster than Mergesort.

3.4 Determining the Runtimes Theoretically

As in Chap. 2, it is possible to determine with mathematical methods how

the runtimes of the algorithms depend on the number n of elements to be

sorted, without having to program the algorithms and measure the time on

a computer. These methods show that a simple sorting algorithm, such as

Sorting by insertion, has runtime proportional to n

Let us now carry out a similar theoretical estimate of the runtime (also

called runtime analysis)forMergesort.

First, let us think about how many comparisons are needed for step 3 of

the algorithm, the merging of two sorted subsequences of length n/2intoone

sorted sequence of length n. The merging procedure ﬁrst compares the two

lowest cards of each subsequence, and then the new complete stack is started

with the smaller of the two. Then we proceed with the two remaining stacks

in the same manner. In each step two cards are compared and the smaller

one is put on the complete stack. Since the complete stack consists of n cards

in the end, at most n comparisons were carried out (exactly, no more than

n − 1).

In order to consider the recursive structure of the entire algorithm let us

once again look at the tree in Fig. 3.1.

22 Helmut Alt

The master at the top has to sort 16 cards. He gives eight to each of the

two helpers; they both give four to each of their two helpers; and so on. The

master at the top in step 3 has to merge two times eight (in general, two times

n/2) cards to a complete sorted sequence of length 16 (n). This takes, as we

saw before, at most 16 (n) comparisons. The two helpers at the level below

merge n/2 cards each, so they need at most n/2 comparisons each, so together

at most n, as well. Likewise, the four helpers at third level merge n/4 cards

each and together again need at most n comparisons; and so on.

So, it can be seen that for each level of the tree at most n comparisons

are necessary. It remains to calculate the number of levels. The ﬁgure shows

that for n = 16 there are four levels. We can see that when descending down

the tree, the length of the subsequences to be sorted decreases from n at the

highest level to n/2 at the second level, and further to n/4, n/8, and so on.

So, it is cut in half from level to level until length 1 is reached at the lowest

level. Therefore, the number of levels is the number of times n can be divided

by 2 until 1 is reached. This number is known to be (cf. also Chap. 1)the

base 2 logarithm of n,log

(n). Since for each level at most n comparisons are

necessary, altogether Mergesort needs at most n log

(n) comparisons to sort

n numbers.

For simplicity, we assumed in our analysis that the length n of the input

sequence always can be divided by 2 without a remainder until 1 is reached.

In other words, n is a power of 2, i.e., one of the numbers 1, 2, 4, 8, 16,....For

other values of n, Mergesort can be analyzed with some more eﬀort. The idea

remains the same and the result is that the number of comparisons is at most

nlog

(n). Here, log

(n) is log

(n) rounded up to the smallest following

integer.

Here, we only estimated the number of comparisons. If this number is

multiplied by the time that the computer running the algorithm needs for a

comparison,

one gets the total time needed for comparisons. This value is

not yet the total runtime, since besides comparisons other operations, such

as for restoring the elements to be sorted and for the organization of the

recursion, are needed. Nevertheless, it can be analyzed that the total runtime

is proportional to the number of comparisons. So, by our analysis, we know

at least that the runtime for Mergesort is proportional to n log

(n).

These considerations explain the superiority of Mergesort over Sorting by

insertion that we observed in the previous section. For that algorithm the

number of comparisons is n(n − 1)/2, as derived in Chap. 2. Indeed, this

function grows much faster than the function n log

(n).

For Quicksort the situation is more complicated. It can be shown that for

certain inputs, e.g., if the input sequence is already sorted, its runtime can

be very large, i.e., proportional to n

. You may get an impression why this is

the case if you follow the algorithm “by hand” on such an input. This case,

For a comparison of two integers a modern computer needs about one nanosecond,

i.e., one billionth of a second.

3 Fast Sorting Algorithms 23

however, only occurs if the element x to split the sequence, the so-called pivot,

is the ﬁrst or the last element in sorted order. If, instead, a random element

from the sequence is chosen, then the probability that the algorithm is slow

is very small. On average, the runtime is also proportional to n log

(n). And,

as our experiments show, the constant factor in front of n log

(n) is obviously

better than that in Mergesort. In practice, Quicksort is indeed the fastest

sorting algorithm, as has also been demonstrated by our experiments in the

previous section.

3.5 Implementation in Java

By the descriptions in Sect. 3.1 the algorithms are already well deﬁned and well

explained. Nevertheless, for readers familiar with the programming language

Java who are interested in the technical details, we will, in addition, give

the implementations of the algorithms. In fact, both algorithms are oﬀered by

Java and can be easily used. Mergesort can be found in the class “Collections”

under the name “Collections.sort” and Quicksort can be found in the class

“Arrays” under the name “Arrays.sort.” These methods can be used not only

for numbers but also for arbitrary objects that are pairwise comparable.

Here, however, we will show self-written and easier to understand methods

for integers. Also, these programs were used for the measurements in Sect. 3.3.

One call of the method is always applied to the parts of an array A whose

boundaries are given.

Let us look at Mergesort ﬁrst. We show ﬁrst the method to merge two

sorted sequences into one sorted sequence:

public static void merge (int[] A, int al, int ar,

int[] B, int bl, int br,

int[] C)

// merges a sorted array-Segment A[al]...A[ar] with

// B[bl]..B[br] to a sorted segment C[0] ...

{ int i = al, j = bl;

for(int k = 0; k <= ar-al+br-bl+1; k++)

{ if (i>ar) // A is finished

{C[k]=B[j++]; continue;}

if (j>br) // B is finished

{C[k]=A[i++]; continue;}

C[k] = (A[i]<B[j]) ? A[i++]:B[j++];

}}

Now Mergesort itself can be easily written as a method in Java:

24 Helmut Alt

public static void mergeSort (int[] A, int al, int ar)

{ // sorts the array-Segment A[al] to A[ar]

if(ar>al) {int m = (ar+al)/2;

// recursive sorting of the halves:

mergeSort(A,al,m);

mergeSort(A,m+1,ar);

// merging into array B :

int[] B = new int[ar-al+1];

merge(A,al,m, A,m+1,ar, B);

// storing hack into A:

for(int i=0;i<ar-al+1;i++) A[al+i] = B[i];

}

The program can be made even faster by saving the storing of array B

to A and applying the recursive calls alternatively to A and B. For simplicity

we didn’t do that here.

Quicksort has an additional advantage over Mergesort by virtue of its not

needing an auxiliary array B but only the array A, which contains the data.

The splitting (step 2 of the algorithm) is done by using a “pointer variable” i.

i starts at the beginning of the segment to be sorted and stops as soon as

an A[i] has been found which is greater than the pivot, i.e., it doesn’t belong

into the left half. At the same time variable j starts from the right end of the

segment going left and stops at elements A[j] that are smaller than the pivot.

If both pointers stop, A[i]andA[j] are swapped and the run continues until

both pointers meet.

public static void swap (int[] A, int i, int j)

{int t = A[i]; A[i] = A[j]; A[j]=t;}

public static void quickSort (int[] A, int al, int ar)

// sorts the segment A[al],...,A[ar]

{if(al<ar)

{

int pivot = A[al], // 1st element as pivot

i=al, j=ar+1;

// splitting:

while(true)

{ while (A[++i] < pivot && i<ar){}

while (A[--j] > pivot && j>al){}

3 Fast Sorting Algorithms 25

if (i<j) swap(A,i,j);

else

break;

}

swap(A,j,al);

quickSort(A,al,j-1);

quickSort(A,j+1,ar);

}

Further Reading and Experiments

For animations of the algorithms presented here, you can search the Internet.

In particular, we recommend the following pages:

http://math.hws.edu/TMCM/java/xSortLab/

http://www.cs.ubc.ca/

∼

harrison/Java/sorting-demo.html

http://cg.scs.carleton.ca/

∼

morin/misc/sortalg/

http://www.tcs.ifi.lmu.de/

∼

gruberh/lehre/sorting/sort.html

On some of those pages, other sorting algorithms and programs in a high-level

programming language are also given.

Sorting by insertion is contained in most of the pages; its runtime is pro-

portional to n

, just as in the case of the frequently presented algorithm Bub-

blesort. Even for small input sequences with 100 or 200 objects to be sorted,

the superiority of Mergesort and Quicksort can be recognized clearly.

Parallel Sorting – The Need for Speed

Rolf Wanka

Universit¨at Erlangen-N¨urnberg, Erlangen, Germany

Since the early days of the development of “general” computing machines,

there has been the idea to also build dedicated devices that are capable of

solving the sorting problem (already addressed in Chaps. 2 and 3) exception-

ally fast. In this chapter, we present a solution of the sorting problem that is

well suited to be implemented as special purpose hardware on a microchip. It

is a so-called parallel sorting algorithm.

When in the 1890s Herman Hollerith built his famous tabulating machine

in order to evaluate the US Census, he also engineered and built an additional

device used to sort the punch cards that stored the collected data. In the

picture above, we see an original Hollerith machine. The “small” device on

the right is a punch card sorting machine. Of course, the cable we see is not for

data transmission, but for electrical power supply. The punch cards get sorted

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0

 Springer-Verlag Berlin Heidelberg 2011

28 Rolf Wanka

by the “sorting by insertion” method we have already encountered in Chap. 2.

In the era of very large-scale integrated circuits, sorting units of course do not

sort punch cards any more, but sort data stored as bits and bytes. Now we

are looking for sorting algorithms that can be realized by modern microchips.

Sorting in Hardware: Comparators and Sorting Circuits

In the following, we present the construction of a hardware sorter. On n

wires, it gets an arbitrarily mixed sequence of n non-negative integer numbers

we call keys. All keys are available simultaneously. We want that the sorter

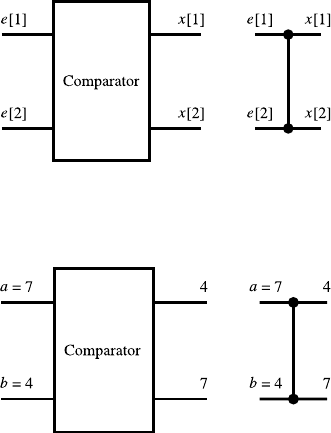
consist of just one kind of module: Comparator. A comparator has two inputs,

e[1] and e[2], and two outputs, x[1] and x[2]. Two arbitrary keys, a and b,

enter the comparator, and, as the output of the comparator, x[1] receives

the smaller key, i.e., x[1] = min{a, b},andx[2] receives the larger key, i.e.,

x[2] = max{a, b}. The following ﬁgure shows two ways to draw a comparator.

In the rest of this chapter, we shall use the right, more compact picture. For

our purposes, we ignore how a comparator is electronically realized.

Thus, the input keys a =7andb = 4 will be processed as follows:

If we have only a single comparator, we may use it to implement the condi-

tional exchange operations in the already introduced algorithms MergeSort

and QuickSort (see Chap. 3). However, as we only have a single compara-

tor, all required conditional exchange operations must be executed one after

another, i.e., sequentially.

4 Parallel Sorting – The Need for Speed 29

Now we design a circuit that consists of many copies of comparators. It

can sort any sequence of n keys much faster than sequential algorithms. We

start with a small, but instructive example of such a circuit consisting of

comparators only. Study the following ﬁgure.

The input of length 4 arrives at the left. It passes through the circuit to

the right. Another term often used instead of circuit is network. The following

simple arguments show that the circuit above consisting of six comparators

can sort any sequence consisting of four keys: No matter on which wire the

minimum key will enter the ciruit on the left, it will always leave it on the

upmost wire x[1]. Analogously, the maximum key will always leave the circuit

on the lowermost wire x[4], no matter which wire was its input wire. Finally,

we see that the last comparator guarantees x[2] ≤ x[3]. Hence, we conclude

that this circuit sorts any input sequence. Therefore, it is called a sorting

circuit.

The next ﬁgure shows how the input sequence (4, 3, 2, 1) is processed by

this circuit. Note that in every step an exchange is actually executed. This

means that in this circuit no comparator is redundant.

We also learn from this ﬁgure that all comparators that are drawn one

below the other may be executed simultaneously. So only four time units will

elapse until the input becomes sorted. Rather than speak of time units, we

speak of parallel steps.

The Bitonic Sorting Circuit: Its Architecture

Can we implement the sequential (non-parallel) sorting algorithms Merge-

Sort and QuickSort from Chap. 3 by comparator circuits because, after

all, they also apply conditional exchange operations as their basic operations?