Vij D.R. Handbook of Applied Solid State Spectroscopy

Подождите немного. Документ загружается.

1. Nuclear Magnetic Resonance Spectroscopy

is sensitive to both these features. In fact, if the molecular motion involves

only one or a few reorientation angles, typical elliptical patterns are observed

and the reorientation angle can be obtained directly from the experimental

spectrum in a model-free approach [7, 84]. It can be accomplished by

measuring the two principal axes of the observed ellipses (a and b, as

indicated in Figure 1.12a), which are related to the reorientation angle

[7, 84]

tanȕ ba .

(1.80)

Figures 1.12a and b show a set of exchange patterns calculated for

different reorientation angles, E

. Elliptical ridges that depend on the

reorientation angle can be easily observed. The 2D patterns were calculated

by only considering a reorientation of E

, i.e., the calculation does not take

into account the back jumps to the original positions. However, in the limit

where the correlation time of the motion is much shorter than the mixing time,

many forward and back jumps may happen during this period.

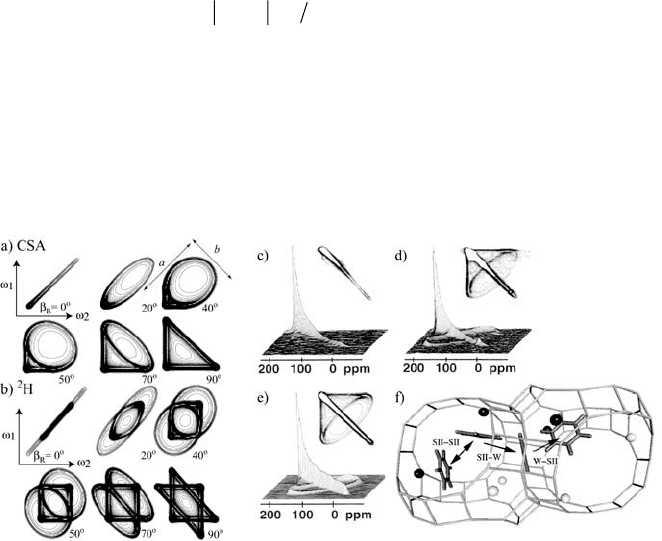
Figure 1.12 2D-exchange powder pattern for K = 0 as a function of the reorientation angle E

Patterns for a) I = ½ (CSA) and b) I = 1 (

H quadrupolar). c)

C 2D-exchange on benzene

adsorbed in the supercage of Ca-LSX zeolite at T = 298 K and t

= 1 ms, and d) at T = 298 K

and t

= 300 ms. e) Simulated 2D-exchange spectrum based on an isotropic distribution of

axially symmetric chemical shift tensors executing discrete jumps with E

= (109 r 3q). f)

Diagram showing the hopping of benzene molecules adsorbed at Ca

cation sites (SII) in a Ca-

LSX zeolite supercage. (Adapted with permission from reference [34]. Copyrights 2005 by

American Physical Society and American Chemical Society)

As a result, even for a simple two-site jump between equally populated

sites, the 2D-exchange spectrum has a diagonal pattern that arises from

molecular segments that, after executing a certain number of jumps, return to

their original position at the end of the mixing time. Actually, if all segments

participate in the molecular reorientations with the same rate, the ratio

between the integral of the diagonal pattern and the integral of the full 2D

pattern gives the probability that a molecular segment has of returning to its

1.7 Molecular Dynamics and Local Molecular Conformation in Solid Materials

initial orientation after t

. In other words, it is the inverse of the number of

sites accessible to the molecular motion.

An example of the application of 2D-exchange NMR for studying

molecular motions can be found in the case of benzene adsorbed in nano and

mesoporous materials, more specifically, benzene adsorbed in supercages of

Ca-LSX zeolites [34]. Figure 1.12c shows the

C 2D-exchange NMR

spectrum of benzene at T = 298 K with t

= 1 ms. The spectrum is mostly

diagonal, indicating the absence of exchange in this time scale. In contrast, a

clear elliptical ridge appears when the mixing time is increased to 300 ms,

Figure 1.12d. Figure 1.12e shows the simulated 2D-exchange spectrum based

on an isotropic distribution of axially symmetric chemical shift tensors

executing discrete jumps with E

= (109 r 3q) among tetrahedrally arranged

sites (E

= 109.5q) and correlation times of the order of the mixing times. The

good agreement between the simulated and experimental spectra confirms the

model for the adsorbed benzene hopping in the supercages of Ca-LSX zeolites

shown in Figure 1.12f.

Another example of the application of 2D-exchange NMR in the study of

discrete jump process is the case of the molecular motions responsible for the

E-relaxation of poly(methyl methacrylate) (PMMA). PMMA belongs to an

important class of glassy polymers, where mechanical and dielectric

properties are strongly affected by the E-relaxation process, which is one of

the most widely studied local relaxations in glassy polymers [85]. Because the

exchange NMR experiments essentially detect reorientations of the

chemical shift anisotropy (CSA) tensors, the molecular motion occurring as

part of the E-relaxation can be well probed by the carbonyl groups, COO. The

COO tensor principal values and its PAS orientation are also well known for

PMMA, Figure 1.13a [86, 87]. The large CSA of COO groups and the fact

that not all segments participate in the ȕ-ҟrelaxation in the exchange time scale,

make the sensitivity considerably low, which might preclude acquisition of

good 2D spectra within a reasonable measuring time. To overcome this

difficulty, isotopic

C labeling in the carbonyl groups was used [86]. The ȕ-

relaxation of PMMA involves rotations of the ester side group around the C-

COO bond (S-ringflip) accompanied by rearrangements of the main chain

(small-angle twists), which occur in several steps as shown in Figure 1.13a

[86, 88, 89]: Starting from a given orientation (I), the asymmetric ester side

group executes a flip coupled to a twist around the main chain axis, which

avoids a steric clash with the local environment (II). Subsequently, after a

new flip (flip-back), also accompanied by small-angle twist, the side group

orientation is slightly different from its original position (III), which results in

a small-angle reorientation of the principal axis system for the carbonyl

group. The 2D

C exchange spectrum of PMMA acquired at T = 333 K is

shown in Figure 1.13b. A simulation of such spectrum using only the 180°

flip, Figure 1.13c, is considerably different from the experimental result,

showing that another molecular motion must be involved in the E-relaxation

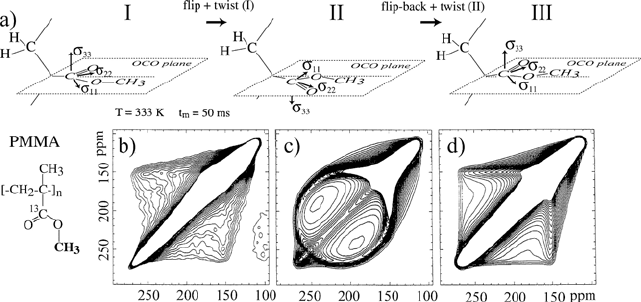
1. Nuclear Magnetic Resonance Spectroscopy

of PMMA. Figure 1.13d shows the simulated spectrum assuming that half of

the side groups reorients by 180° flip accompanied by small-angle twist with

average amplitude of 20q, while the other half executes only rocking motion

around the main chain with an average amplitude of 7q. The agreement

between the experimental and simulated spectra is remarkable, showing that

the E-relaxation of PMMA involves molecular motions with this geometry.

The correlation times obtained from these studies have the same values and

temperature dependence as those reported from dielectric and dynamic-

mechanical studies, confirming the direct connection between the molecular

motions and the E-relaxation of PMMA [85, 86].

Other studies on this topic include the merging between the D- and E-

relaxation in other poly(alkyl methacrylate)s, as well as the conformational

randomization that occurs in temperatures well above their glass transitions

[90–92]. In all these applications,

C and

H 2D-exchange NMR were used as

the main tools for elucidating the origin of the dynamic processes.

Figure 1.13 2D-exchange NMR study of E-relaxation of PMMA. a) PAS tensor orientation for

the COO groups in PMMA during the molecular rotations responsible by the E-relaxation. b)

2D-exchange NMR spectrum of

COO labeled PMMA at 333 K. c) Simulation of the COO

flip in PMMA. d) Simulation considering the motional process discussed in the text. (Adapted

More complex motions, such as the case of the E-relaxation in PMMA

discussed above, usually lead to a distribution of reorientation angles,





ȕR .

In these cases, considering axially symmetric tensors, the 2D-exchange

spectrum





12m

Ȧ ,Ȧ ,St can be simulated as a





ȕR weighted superposition of

2D spectra calculated for a specific reorientation angle,

ȕ ,





ȕ 12m

Ȧ ,Ȧ ,St,

i.e.,













12m Rȕ 12m R

Ȧ ,Ȧ , ȕȦ,Ȧ , ȕStRS td

(1.81)

1.7 Molecular Dynamics and Local Molecular Conformation in Solid Materials

In this equation the upper limit of the integral is 90q because of the

symmetry property of the 2D-exchange spectrum for axially symmetric

tensors, i.e.,









ȕ 12m 12m

180 ȕ

Ȧ ,Ȧ , Ȧ ,Ȧ ,StS t



[7, 84]. Thus, if the motion

occurs with a distribution of reorientation angles no defined ridges appear in

the 2D-exchange spectrum, but the spectral intensity is spread out. The 2D-

exchange patterns can be calculated using equation (1.81) in order to obtain

the distribution of reorientation angles, and, consequently, the average

amplitude of the motion.

An even more complicated situation can be found in the cases where the

motion not only involves a distribution of reorientation angles, but also a

distribution of correlation times. This is the case of the molecular motions in

many amorphous polymers at temperatures close to their glass transitions

temperatures T

. In these cases, the molecular motions have a diffusive

character, which can be taken into consideration by calculating the

distribution of reorientation angles from the diffusion equation that describes

the rotational diffusion process [71]. In general, for rotational diffusion the

reorientation angle distribution depends not only on the kind of diffusion

process, but also on the ratio between the mixing time used in the experiment

and the correlation time of the motion, R(E

, t

). Consequently, for the

general case where a diffusive motion occurs following a distribution of

correlation times, the 2D-exchange spectrum can be calculated as:











12m RmC Cȕ 12m C R

Ȧ ,Ȧ , ȕ , ĲĲ Ȧ,Ȧ , ĲȕSt RtgS tdd

³³

(1.82)

Therefore, when exchange is due to a diffusive motion a characteristic line

shape that depends on R (E

, t

) is observed.

H 2D-exchange NMR pattern can also be simulated by adding the

two-mirror symmetric spectra, resulting in the patterns shown in Figure 1.12b.

Because

H is a spin 1 nucleus and the quadrupolar interaction anisotropy is

quite large in most cases, for obtaining absorptive undistorted

2D-exchange spectra it is necessary to select the evolution of the proper

coherences in the density matrix to encode the information on the molecular

motion and also to perform solid-echo acquisition to avoid the dead time

problem [54]. This is accomplished by the pulse sequence shown in Figure

1.11b, where

= 55q is used in order to maximize the detected signal,

together with the solid-echo detection (pulse

is set to 90q with appropriate

phase). All the interpretations in terms of the probability densities also hold

true for

H 2D-exchange, and the time signal obtained after the pulse

sequence of Figure 1.11b can be written as:







2m1

ȦȦt

ȦĲ ȦĲ

12m

detect mix evol

solid-echo

,, 1 01

it t i

Tii

St t t e e e e e P

r3r





 

(1.83)

A more general treatment can be done considering also the cases where the

correlation times of the molecular motions are comparable or smaller than the

1. Nuclear Magnetic Resonance Spectroscopy

maximum evolution periods, t

and t

. In these circumstances, molecular

motions can also occur during the evolution periods, which can produce

pronounced changes in the 2D spectral shapes. Fortunately, using the same

theory presented above, these cases can also be treated. This is accomplished

by adding the effect of exchange of frequencies during the evolution,

detection, and echo periods to the expression for the NMR signal [69, 93],









ȦȦĲȦĲ Ȧ

12m

mix

detect solid-echo evol

,, 1 01

it i i it

St t t e e e e e P

3r 3r 3 3r

 



   

(1.84)

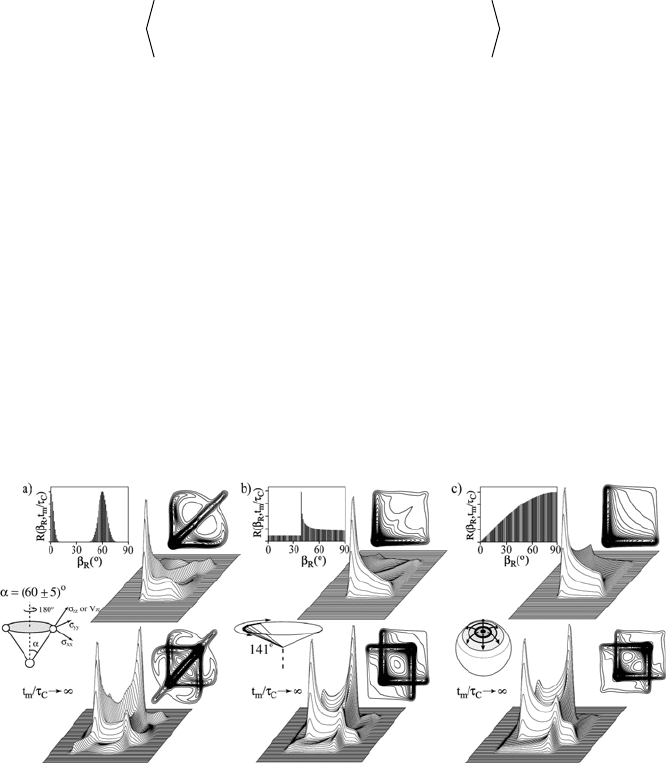
Figure 1.14 shows characteristic CSA (K = 0) and

H exchange patterns for

different motional models. In Figure 1.14a the motional model is a two-site

jump occurring with a distribution of reorientation angles, R(E

, t

), as

shown in the inset. The elliptical ridge characteristic of E

= 60q is evident in

the simulations, but there is also a diagonal pattern which accounts for

segments that jump forward and backward during t

. In Figure 1.14b, the

model assumed is uniaxial rotational diffusion (or diffusion in a cone) for the

case where t

>> W

[7, 71]. An elliptical ridge characteristic of the singularity

in R(E

, t

) is also observed in this case, but no pronounced diagonal is

present. This model is typical for molecules that rotate inside restricted

spaces. Figure 1.14c shows the 2D-exchange patterns obtained for isotropic

rotational diffusion also in the limit t

>> W

[7, 71]. The intensity is spread

out over the whole frequency range and there is no diagonal pattern. This is so

because this model assumes a small-step diffusion between successive sites,

making the probability of returning to an original position negligible.

Figure 1.14 Typical 2D-exchange NMR patterns for different types of motions: a) CSA and

2D patterns for two-site jump motion occurring with a distribution of reorientation angles; b)

for isotropic rotational diffusion in the limit t

>> W

; and c) for isotropic rotational diffusion

motions in the limit t

>> W

Information about the time scale of molecular motions can also be

obtained in 2D-exchange NMR experiments. A simple way of achieving that

directly from the experimental spectra is accompanying the build-up of the

off-diagonal exchange intensity (I

exch

) as a function of t

. In this case the I

exch

1.7 Molecular Dynamics and Local Molecular Conformation in Solid Materials

vs. t

curve directly provides the two-time correlation function of the slow

motion, allowing the estimation of the correlation time and its distribution.

Some of the most elegant examples of the application of

H and

2D-exchange NMR can be found in the studies of rotational diffusion

processes [69, 71, 93, 94]. Among these examples, particular attention must

be given to the rotational motions responsible by the D-relaxation (glass

transition) in supercooled glass-forming systems. Amorphous systems in the

glass transition range exhibit particular dynamic properties such as non-

exponential D-relaxation [36, 73, 95–98]. This is attributed to the presence of

a broad distribution of correlation times in the molecular motions responsible

for this process.

H line shape analysis indicated that D-relaxation also occurs

with a distribution of reorientation angles, which was further elucidated by

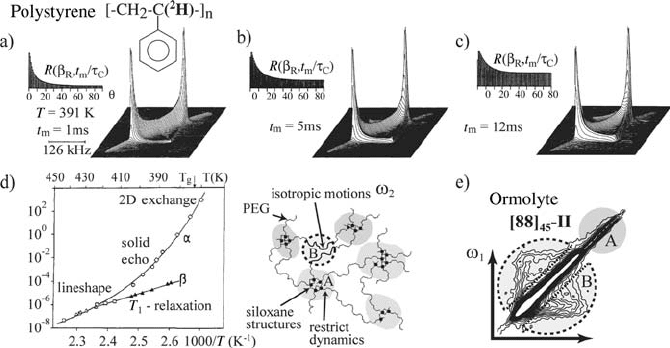
2D-exchange NMR performed in many of these systems. One example is the

study of the D-relaxation in amorphous polystyrene ([C

-PS]

) [69, 94, 99],

where the hydrogen in the CH backbone groups was replaced by

H in order

to probe the main chain motion of PS. Figure 1.15 shows

H 2D-exchange

spectra of polystyrene at 391 K (18 K above its glass transition temperature)

for mixing times of 1, 5, and 12 ms. Instead of characteristic elliptical ridges,

the 2D spectrum has a broad distribution of intensities as expected for

diffusive motions. In fact, the ridges parallel to the frequency axes forming

prominent square ridges and the spectral intensity covering the whole 2D-

plane reflect the large-angle reorientation of the chain segments.

Figure 1.15 a)–c)

H 2D-exchange NMR spectra of amorphous PS for different mixing times

with the corresponding reorientation angle distributions. d) Logarithmic plot of the correlation

times vs. inverse of temperature for polystyrene obtained by different NMR methods. e)

2D-exchange NMR of Type II ormolytes for t

= 200 ms. (Adapted with permission from

1. Nuclear Magnetic Resonance Spectroscopy

The fact that the exchange intensities are spread out over the whole

frequency range means that a particular C-

H bond has a finite probability to

be found in any orientation with respect to the magnetic field after the mixing

time, regardless of its starting orientation before the mixing time. Thus, the

large-angle reorientations are a result of many steps of small-angle motions

that occurred during t

. This was confirmed by performing simulations based

on isotropic rotational diffusion (not shown) and comparing them with the

experimental spectra in order to determine the reorientation angle distribution,

R(E

, t

), shown in Figure 1.15. The behavior of R(E

, t

) as a function

of t

was described by a model that assumes small-step isotropic rotational

diffusion and a log-Gaussian distribution of correlation times with full-width-

at-half-height of 3.0 decades and centered around the mean value of 6 ms

[69]. Similar methods were used to study molecular dynamics in

polyisopropene [93], atactic polypropylene [94], and blends of polyisoprene

and poly(vinyl ethylene) [7].

Figure 1.15d also shows a plot of the correlation times as a function of the

inverse of temperature (Arrhenius plot) obtained by various

H experiments

(

H line shape analysis or broad-line, solid-echo experiments,

H 2D-

exchange NMR, and spin-lattice relaxation). The behavior of the correlation

times obtained by

H line shape analysis, solid-echo experiments, and

H 2D-

exchange NMR can be fitted by the Williams-Landel-Ferry equation [100],

which is usual for describing the temperature dependence of the polymer

structural dynamics above T

. On the other hand, the correlation times

obtained by spin-lattice relaxation measurements follow an Arrhenius

behavior, characteristic of local motions in polymers (E-relaxation). Using the

different NMR experiments it was possible to follow the dynamics in a broad

range of frequencies and correlate the molecular dynamics with structural

relaxation processes.

An example of

C 2D-exchange NMR applied to investigate molecular

dynamics in a more complex system can be found in the study of the polymer

molecular dynamics in siloxane/poly(ethylene glycol) nanocomposites

also called ormolytes [79]. This hybrid system belongs to a family of

versatile compounds, classified as di-ureasils, in which polyether-based

chains are grafted on both ends to a siliceous backbone through urea

functionalities (Type II ormolytes), see Figure 1.15e [38]. The polymer chain

in Type II ormolytes have the following chemical structure:

{

3/2

OSi(CH

)

NHCONH(CH

)

[OCH

]

O(CH

)

NHCONH(CH

)

SiO

3/2

The organic part of the ormolyte is composed of a linker group

((CH

)

NHCONH(CH

)

) and n ethylene glycol repeat units OCH

Figure 1.15e shows the

C 2D-exchange spectra for a Type II ormolyte

sample with 45 OCH

repeat units and 88 wt% of PEG. The spectrum

clearly shows two distinct regions. In the spectral region A the NMR signal is

exclusively attributed to

C nuclei in the linkage group. The observed

exchange pattern is fully diagonal, indicating that these groups do not move in

the ms time scale. On the other hand, in region B a featureless off-diagonal

1.7 Molecular Dynamics and Local Molecular Conformation in Solid Materials

exchange pattern is observed, indicating that the motion of the OCH

groups do not involve discrete jump angles. Figure 1.15e is a clear, model-

free picture of the strong hindrance to the molecular motion due to the

siloxane structure, since it directly reveals the distinct dynamic behavior of

segments near the siloxane structures.

It is difficult to use 2D-exchange NMR in cases where only a small

fraction of the segments take part in the molecular motions, because the

strong and sharp diagonal ridge (due to the nonmoving segments) overwhelms

the weak and broad ridges from the moving groups. This is particularly

prominent for small-angle reorientations, where the exchange intensity is

concentrated near the diagonal of the 2D spectrum. To overcome this

difficulty, a modified version of the 2D-exchange experiment named 2D pure

exchange NMR (2D-PUREX) has been developed [101–104]. In these

experiments extra pulses with adequate phase cycling, extra evolution periods,

and spectral subtraction are used together to produce a 2D-exchange spectrum

modulated by



sin ȦȦĲ2 , where W is the extra evolution period added

to the pulse sequence; see Figure 1.16 (top).

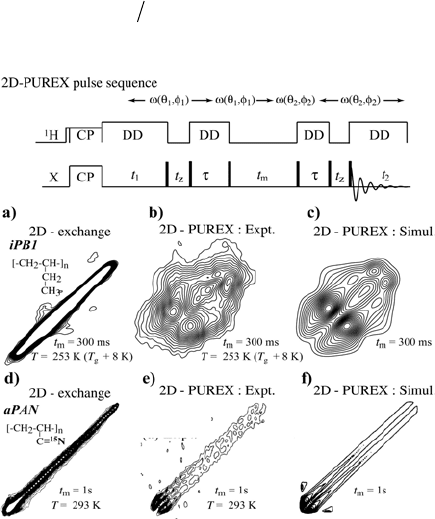
Figure 1.16 a)

C 2D-exchange NMR spectrum of iPB at T = 253 K. b)

C 2D-PUREX

spectrum of iPB at T = 253 K. c) Simulation of the

C 2D-PUREX spectrum of iPB using

isotropic rotational diffusion model with a log-Gaussian distribution of correlation times with

width of 1.5 decades. The CSA principal values were taken from reference [53]. d)

N 2D-

exchange spectrum of a PAN at T = 293 K. e)

N 2D-PUREX spectrum of aPAN at T = 293 K.

f) Simulation of

N 2D-PUREX spectrum using a restricted diffusion model with average

Elsevier)

1. Nuclear Magnetic Resonance Spectroscopy

Because of the



sin ȦȦĲ2 spectral modulation, segments that do

not reorient during t

, Z

= Z

, do not contribute to the exchange signal.

Consequently, only segments reorienting on the ms to s time scale appear in

the resulting 2D spectrum. One example of the performance of the

2D-PUREX method is shown in Figures 1.16a–c, where the technique was

applied to the crystal form I of the semicrystalline polymer isotactic poly(1-

butene), ([CH

-CH-R-]

-iPB1), at a temperature slightly above its glass

transition. The regular 2D-exchange spectrum, Figure 1.16a, shows a

pronounced diagonal ridge that arises from the rigid crystalline portion, and

an almost imperceptible off-diagonal pattern, from the mobile amorphous

region. In contrast, in the 2D-PUREX spectrum the off-diagonal intensity

characteristic of diffusive motions is clearly observed, while the diagonal

ridge is suppressed (Figure 1.16b). The simulation of the 2D-PUREX patterns

using the isotropic rotation diffusion model reveals the good reliability of the

method, Figure 1.16c [102].

The usefulness of the 2D-PUREX technique for detecting small-angle

motions was also demonstrated in the amorphous polymer atactic

poly(acrylonitrile) ([C

-aPAN), Figures 1.16d–f. At 293 K, near

diagonal exchange intensity was observed in the 2D-exchange spectrum,

Figure 1.16d. However, it was not possible to attribute it to small-angle

motion because of the superposition of the dominant diagonal pattern. To

confirm the existence of the slow small-angle motions, 2D-PUREX was

carried out (Figure 1.16e). In this experiment the diagonal ridge was

suppressed, and the off-diagonal signals near the diagonal were clearly

detected, showing the presence of slow small-angle reorientation of the aPAN

side chain. In this case the

N 2D-PUREX spectrum can be simulated by a

restrict diffusion process with average amplitude of 20q [57].

Another important variant of the 2D-exchange experiment is the so-called

rotor synchronized 2D-MAS exchange technique. This method was initially

proposed by Veeman et al. [105], who introduced the idea of “rotor

synchronization” of the pulse sequence, i.e., making sure that t

is an integer

number of rotation periods, t

= Nt

so that the precession of the

magnetization resumes at the same rotor orientation where it was at the

beginning of the mixing time. Otherwise, reorientations of segments

relative to the external field occur due to the macroscopic rotation of the

sample (MAS) and overwhelm the more subtle effects of intrinsic segmental

reorientations. In later experiments, synchronization with the beginning of the

evolution period was also used, in order to achieve pure-phase 2D-MAS

exchange spectra [106]. The principle of the experiment is the same as the

conventional exchange NMR methods for nonrotating solids discussed above,

i.e., it correlates the anisotropic NMR frequencies in two different periods of

time (

t and

t ) separated by a long synchronized mixing time

t [83]. The

appearance of off-diagonal peaks in the two-dimensional spectra is directly

associated with changes in the orientation-dependent NMR frequencies. When

1.7 Molecular Dynamics and Local Molecular Conformation in Solid Materials

performed under slow-spinning frequencies relative to the anisotropy of the

interaction used to probe the molecular motion, the spectrum consists of a 2D

sideband pattern, which depends on the characteristics of the slow molecular

reorientations. Because isotropic chemical shifts may also change according

to the local conformation of a given molecular segment, MAS exchange is

also a powerful tool for studying conformational dynamics. In the absence of

molecular motion during

t , a normal MAS sideband pattern along the

diagonal is observed. In the case of molecular motions that only change the

orientation of the chemical shift tensor principal axis, cross-peaks, labeled as

auto-cross-peaks, appear at









1 2 iso R iso R

Ȧ ,ȦȦ Ȧ,ȦȦ

MN   ,

(1.85)

where

iso

Z is the isotropic chemical shift frequency of a nucleus at a given

molecular site i;

Z is the angular spinning frequency, and M and N are the

order of the spinning sidebands. On the other hand, if the exchange process

involves a change in the isotropic chemical shift, cross-peaks, labeled

hetero-cross-peaks, appear at









1 2 iso R iso R

Ȧ ,ȦȦ Ȧ,ȦȦ

MN   ,

(1.86)

where i and j indicate the change in the isotropic chemical shift of a given

nucleus. Thus, if there is an exchange process that changes the isotropic

chemical shift, cross-peaks linking isotropic chemical shift frequencies appear

in the centerband (M = N = 0) even if no sidebands are observed, i.e., at high

spinning frequencies.

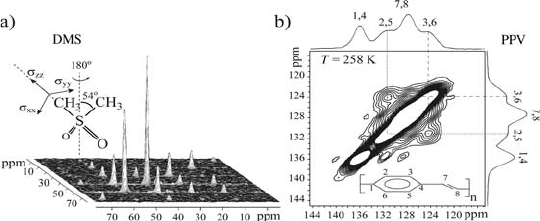
Figure 1.17a shows a rotor synchronized 2D-MAS exchange NMR of the

molecular crystal dimethylsulfone (DMS) at a spinning frequency of 1.5 kHz

and mixing time of 20 ms [83]. At 293 K, DMS undergoes rotations around

the main molecular axis with correlation times of ~10 ms, which lead to a

reorientation of the principal axis

by 108° [107], resulting in the 2D

sideband pattern observed in Figure 1.17a.

Figure 1.17 a)

C rotor synchronized 2D-MAS exchange NMR of the molecular crystal DMS

at T = 293 K, Q

= 1.5 kHz and t

= 20 ms. b)

C rotor synchronized 2D-MAS exchange of

PPV at T = 258 K, Q

= 7.5 kHz and t

= 200 ms. (Adapted from reference [83], Copyright

Institute of Physics)