Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

16.4 Multivariable Regression 631

Multicollinearity can be diminished by excluding problematic variables

causing the collinearity in the ﬁrst place. Alternatively, groups of variables

can be combined and merged into a single variable.

Another measure is to keep all variables but “condition” matrix X

X by

adding kI, for some k

> 0, to the normal equations. There is a tradeoff: the

solutions of (X

X +kI)

β = X

y are more stable, but some bias is introduced.

lambdas = eig(X’

X);

K = max(lambdas)/min(lambdas)

Ki = max(lambdas)./lambdas

Xprime = [];

for k=2:p

Xkbar = mean(X(:,k));

sk = std( X(:,k));

Xprimek = 1/sqrt(n-1) .

(X(:,k)- Xkbar

ones(n,1) )/sk;

Xprime = [Xprime Xprimek];

end

RXX = Xprime’

Xprime;

VIF = diag (inv(RXX));

VIF’

% 2.2509 33.7869 2.2566 16.1634 4.4307 10.6846 13.3467

%15.1583 7.9615 4.8288 1.9455 3.6745 2.1934 3.3796

Alternatively, for most of the above calculations one can use MATLAB’s

regstats or diagnostics.m,

s = regstats(Y,Z,’linear’,’all’);

[index,res,stud

res,lev,DFFITS1,Cooks

D,DFBETAS]=diagnostics(Y,Z);

16.4.2.3 Variable Selection in Regression

Model selection involves ﬁnding a subset of predictors from a large number of

potential predictors that is optimal in some sense.

We deﬁned the coefﬁcient of determination R

as the proportion of model-

explained variability, and it seems natural to choose a model that maximizes

. It turns out that this is not a good idea since the maximum will always be

achieved by that model that has the maximal number of parameters. It is a

fact that R

increases when even a random or unrelated predictor is included.

The adjusted R

penalizes the inclusion of new variables and represents a

better criterion for choosing a model. However, with k variables there would

be 2

possible candidate models, and even for moderate k this could be a

formidable number.

There are two mirroring procedures, forward selection and backward selec-

tion, that are routinely employed in cases where checking all possible models

is infeasible. Forward selection proceeds in the following way.

STEP 1. Choose the predictor that has the largest R

among the models with a

single variable. Call this variable x

632 16 Regression

STEP 2. Assume that the model already has k variables, x

,..., x

, for some k ≥ 1.

Select the variable x

k+1

that gives the maximal increase to R

and reﬁt the model.

STEP 3. Denote by SSR(x

,..., x

) the regression sum of squares for a regression ﬁt-

ted with variables x

,..., x

. Then R(x

k+1

,..., x

) = SSR(x

,..., x

k+1

)−SSR(x

,..., x

)

is the contribution of the (k

+1)st variable and it is considered signiﬁcant if

R(x

k+1

,..., x

)/MSE > F

1,n−k−1,α

. (16.5)

If relation (16.5) is satisﬁed, then variable x

k+1

is included in the model. Increase k

by one and go to STEP 2.

If relation (16.5) is not satisﬁed, then the contribution of x

k+1

is not signiﬁcant, in

which case go to STEP 4.

STEP 4. Stop with the model that has k variables. END

The MSE in (16.5) was estimated from the full model. Note that the for-

ward selection algorithm is “greedy” and chooses the single best improving

variable at each step. This, of course, may not lead to the optimal model since

in reality variable x

, which is the best for one-variable models, may not be

included in the best two-variable model.

Backward stepwise regression starts with the full model and removes vari-

ables with insigniﬁcant contributions to R

. Seldom do these two approaches

end with the same candidate model.

MATLAB’s Statistics Toolbox has two functions for stepwise regression:

stepwisefit, a function that proceeds automatically from a speciﬁed initial

model and entrance/exit tolerances, and

stepwise, an interactive tool that al-

lows you to explore individual steps in a process.

An additional criterion for the goodness of a model is the Mallows C

. This

criterion evaluates a proposed model with k variables and p

= k +1 parame-

ters. The Mallows C

is calculated as

=(n − p)

−n +2p,

where s

is the MSE of the candidate model and

is an estimator of σ

usually taken to be the best available estimate. The MSE of the full model is

typically used as



A common misinterpretation is that in C

, p is referred to as the num-

ber of predictors instead of parameters. This is correct only for models with-

out the intercept (or when 1 from the vector of ones in the design matrix is

declared as a predictor).

Adequate models should have a small C

that is close to p. Typically, a

plot of C

against p for all models is made. The “southwesternmost” points

close to the line C

= p correspond to adequate models. The C

criterion is

also employed in forward and backward variable selection as a stopping rule.

Bayesian Multiple Regression. Next we revisit

fat.dat with some

Bayesian analyses. We selected four competing models and compared them

16.4 Multivariable Regression 633

using the Laud–Ibrahim predictive criterion, LI. Models with smaller LI are

favored.

Laud and Ibrahim (1995) argue that agreement of model-simulated pre-

dictions and original data should be used as a criterion for model selection. If

for y

responses

i,new

are hypothetical replications according to the posterior

predictive distribution of competing model parameters, then

i=1

i,new

− y

)

+Var (

i,new

)

measures the discrepancy between the observed and model-predicted data. A

smaller LI is better. The ﬁle

fat.odc performs a Laud–Ibrahim Bayesian

model selection and prefers model #2 of the four models analyzed.

#fat.odc

model{

for(j in 1:N ){

# four competing models

mu[1, j] <- b1[1] + b1[2]

age[j] + b1[3]

wei[j] + b1[4]

hei[j] +

b1[5]

adip[j] + b1[6]

neck[j] + b1[7]

chest[j] +

b1[8]

abd[j] + b1[9]

hip[j] + b1[10]

thigh[j] +

b1[11]

knee[j]+b1[12]

ankle[j]+b1[13]

biceps[j] +

b1[14]

forea[j] + b1[15]

wrist[j]

mu[2, j] <- b2[1]+b2[2]

wei[j]+b2[3]

adip[j]+b2[4]

abd[j]

mu[3, j] <- b3[1]+b3[2]

adip[j]

mu[4, j] <- b4[1]

wei[j]+b4[2]

abd[j]+b4[3]

abd[j]+b4[4]

wrist[j]

}

#LI - Laud-Ibrahim Predictive Criterion. LI-smaller-better

for(i in 1:4 ){

tau[i] ~ dgamma(2,32)

LI[i] <- sqrt( sum(D2[i,]) + pow(sd(broz.new[i,]),2))

# data sets 1-4 for different models

for (j in 1:N) {

broz2[i,j] <- broz[j]

broz2[i,j] ~ dnorm(mu[i,j],tau[i])

broz.new[i,j] ~ dnorm(mu[i,j],tau[i])

D2[i,j] <- pow(broz[j]-broz.new[i,j],2)

}

# Compare predictive criteria between models i and j

# Comp[i,j] is 1 when LI[i]<LI[j], i-th model better.

for (i in 1:3) { for (j in i+1:4)

{Comp[i,j] <- step(LI[j]-LI[i])}}

# priors

for (j in 1:15) { b1[j] ~ dnorm(0,0.001)}

for(j in 1:4) { b2[j] ~ dnorm(0,0.001)

b4[j] ~ dnorm(0,0.001)}

for(j in 1:2) { b3[j] ~ dnorm(0,0.001)}

}

#DATA 1: Load this first

634 16 Regression

list(N = 252)

# DATA2: Then load the variables

broz[] age[] wei[] hei[] ... biceps[] forea[] wrist[]

12.6 23 154.25 67.75 ... 32.0 27.4 17.1

23.4 38.5 93.6 83.00 ... 30.5 28.9 18.2

...248 lines deleted...

25.3 72 190.75 70.50 ... 30.5 29.4 19.8

30.7 74 207.50 70.00 ... 33.7 30.0 20.9

END

#the line behind ’END’ has to be empty

# INITS (initialize by loading tau’s

# and generating the rest

list(tau=c(1,1,1,1))

The output is given in the table below. Note that even though the posterior

mean of

LI[4] is smaller that that of LI[2], it is the posterior median that mat-

ters. Model #2 is more frequently selected as the best compared to model #4.

mean sd MC error val2.5pc median val97.5pc start sample

LI[1] 186.5 209.2 17.63 84.0 104.6 910.5 1001 20000

LI[2] 96.58 23.46 1.924 85.08 93.14 131.2 1001 20000

LI[3] 119.6 5.301 0.03587 109.4 119.5 130.2 1001 20000

LI[4] 94.3 4.221 0.03596 86.33 94.2 103.0 1001 20000

Comp[1,2] 0.2974 0.4571 0.02785 0.0 0.0 1.0 1001 20000

Comp[1,3] 0.5844 0.4928 0.03939 0.0 1.0 1.0 1001 20000

Comp[1,4] 0.3261 0.4688 0.03008 0.0 0.0 1.0 1001 20000

Comp[2,3] 0.9725 0.1637 0.01344 0.0 1.0 1.0 1001 20000

Comp[2,4] 0.5611 0.4963 0.01003 0.0 1.0 1.0 1001 20000

Comp[3,4] 5.0E-5 0.007071 4.98E-5 0.0 0.0 0.0 1001 20000

More comprehensive treatment of Bayesian approaches in linear regres-

sion can be found in Ntzoufras (2009).

16.5 Sample Size in Regression

The evaluation of power in a regression with p−1 variables and p parameters

(when an intercept is present) requires speciﬁcation of a signiﬁcance level and

precision. Suppose that we want a power such that a total sample size of n

61 would make R

= 0.2 signiﬁcant for α = 0.05 and the number of predictor

variables p

−1 =3. Cohen’s effect size here is deﬁned as f

/(1−R

). Recall

that values of f

≈0.01 correspond to small, f

≈0.0625 to medium, and f

≈

0.16 to large effects. Note that from f

= R

/(1 −R

) one gets R

= f

/(1 + f

which can be used to check the adequacy of the elicited/required effect size.

The power, similarly as in ANOVA, is found using the noncentral F-

distribution,

16.6 Linear Regression That Is Nonlinear in Predictors 635

1 −β =P(F

(p −1, n − p,λ) > F

−1

(1 −α, p −1, n − p)), (16.6)

where

λ = n f

is the noncentrality parameter.

Example 16.4. For p

= 4, R

= 0.2, that is, f

= 0.25 (an X-large effect size),

and a sample size of n

= 61, one gets λ = 61 ×0.25 = 15.25, and a power of

approx. 90%.

p=4; n=61; lam=15.25;

1-ncfcdf( finv(1-0.05, p-1, n-p), p-1, n-p, lam)

% ans = 0.9014

16.6 Linear Regression That Is Nonlinear in Predictors

In linear regression, “linear” concerns the parameters, not the predictors. For

instance,

=β

+²

, i =1,..., n

and

=²

×exp{β

+β

}, i =1,..., n

are examples of a linear regression. There are many functions where x and y

can be linearized by an obvious transformation of x or y or both; however, one

needs to be mindful that the normality and homoscedasticity of errors is often

compromised. In such a case, ﬁtting a regression is simply an optimization

task without natural inferential support. Bayesian solutions involving MCMC

are generally more manageable as regards inference (Bayes estimators, credi-

ble sets, predictions).

An example where errors are not affected by the transformation of vari-

ables is a polynomial relationship between x and y postulated as

=β

+β

+···+β

+²

, i =1,..., n,

which is in fact a linear regression. Simply, the k predictors are x

= x

, ..., x

= x

,and estimating the polynomial relationship is straightforward.

The example below is a research problem in which a quadratic relationship is

used.

Example 16.5. Von Willebrand Factor. Von Willebrand disease is a bleed-

ing disorder caused by a defect or deﬁciency of a blood clotting protein called

von Willebrand factor. This glue-like protein, produced by the cells that line

636 16 Regression

blood vessel walls, interacts with blood cells called platelets to form a plug that

prevents bleeding. In order to understand the differential bonding mechanics

underlying von Willebrand-type bleeding disorders, researchers in Dr. Larry

McIntire’s lab at Georgia Tech studied the interactions between the wild-type

platelet GPIba molecule (receptor) and wild-type von Willebrand Factor (lig-

and).

The mean stop time rolling parameter was calculated from frame-by-frame

rolling velocity data collected at 250 frames per second. Mean stop time indi-

cates the amount of time a cell spends stopped, so it is analogous to the bond

lifetime. This parameter, being an indicator for how long a bond is stopped

before the platelet moves again, can be used to assess the bond lifetime and

off-rate (Yago et al., 2008).

For the purpose of exploring interactions between the force and the mean

stop times, Ficoll 6% is added to increase the viscosity.

Data are courtesy of Dr. Leslie Coburn. The mat ﬁle

coburn.mat contains

the structure

coburn with data vectors coburn.fxssy, where x = 0, 6 is a

code for Ficoll absence/presence and

y = 1, 2, 4, ..., 256 denotes the shear

stress (in dyn/cm

). For example, coburn.f0ss16 is a 243×1 vector of mean stop

times obtained with no Ficoll, under a shear stress of 16 dyn/cm

Shear Stress 2 4 8 16 32 64 128 256

Shear Number 1 2 3 4 5 6 7 8

Mean Stop Time f0ss2 f0ss4 f0ss8 f0ss16 f0ss32 f0ss64 f0ss128 f0ss256

Sample Size 26 57 157 243 256 185 62 14

We ﬁt a regression on the logarithm of mean stop time log2mst, with no Fi-

coll present, as a quadratic function of share stress (dyn/cm

). This regression

is linear (in parameters) with two predictors,

shear and the squared shear,

shear2=shear

The regression ﬁt is

log2mst

=−6.2423 +0.8532 shear −0.0978 shear2.

Regression is signiﬁcant (F

= 63.9650, p =0); however, its predictive power is

rather weak, with R

=0.1137.

Figure 16.10 is plotted by the script

coburnreg.m.

%coburnreg.mat

load ’coburn.mat’;

mst=[coburn.f0ss2; coburn.f0ss4; coburn.f0ss8; coburn.f0ss16; ...

coburn.f0ss32; coburn.f0ss64; coburn.f0ss128; coburn.f0ss256];

shearn = [1

ones( 26,1); 2

ones( 57,1); 3

ones(157,1); ...

ones(243,1); 5

ones(256,1); 6

ones(185,1); ...

ones( 62,1); 8

ones( 14,1)];

shearn2 = shearn.^2; %quadratic term

16.7 Errors-In-Variables Linear Regression* 637

0 2 4 6 8

−7

−6

−5

−4

−3

−2

−1

log

(dyn/cm

)

log

(mst)

−3 −2 −1 0 1 2 3

0.1

0.2

0.3

0.4

0.5

(a) (b)

Fig. 16.10 (a) Quadratic regression on log mean stop time. (b) Residuals ﬁtted with normal

density.

%design matrix

X = [ones(length(shearn),1) shearn shearn2];

[b,bint,res,resint,stats] = regress(log2(mst), X) ;

%b0=-6.2423, b1=0.8532, b2 =-0.0978

stats %R2, F, p, sigma2

%0.1137 63.9650 0.0000 0.5856

16.7 Errors-In-Variables Linear Regression*

Assume that in the context of regression both responses Y and covariates X

are measured with error. This is a frequent scenario in research labs in which

it would be inappropriate to apply standard linear regression, which assumes

that covariates are designed and constant.

This scenario in which covariates are observed with error is called errors-

in-variables (EIV) linear regression. There are several formulations for EIV

∼ N (β

+β

,σ

)

∼ N (ξ

,σ

In an equivalent form, the regression is

E y

=β

+β

=β

+β

, i =1, . .., n,

and the inference on parameters

and β

is made conditionally on ξ

. To

make the model identiﬁable, a parameter

η =

is assumed known. Note that

we do not need to know individual variances, just their ratio.

If the observations (x

, y

), i =1,..., n produce sums of squares S

−

, S

− y)

, and S

−x)(y

− y), then

i i

1,... , n, the EIV regression model is

regression (Fuller, 2006). For pairs from a bivariate normal distribution (x

, y ), i =

638 16 Regression

−

−ηS

) +

−ηS

)

+4ηS

2ηS

, (16.7)

= y −

The estimators of the errors are

1 +η

i=1

−(

)

When

η = 1 (variances of errors are the same), the solution in (16.7) co-

incides with numerical least-squares minimization, while for

η = 0 (no errors

in covariates,

= 0), we are back to the standard regression where

(Exercise 16.16).

Example 16.6. Grifﬁn et al. (1945) reported plasma volume (in cc) and cir-

culating albumin (in gm) for n

= 58 healthy males. Both quantities were

measured with error and it was assumed that the variance of plasma mea-

surement exceeded the variance of circulating albumin by 200 times. Using

EIV regression, establish an equation that would be used to predict circulat-

ing albumin from plasma volume. The data are given in

circalbumin.dat,

where the ﬁrst column contains plasma volume and the second is albumin.

The script

errorinvar.m calculates the following EIV regression equation:

E y

=0.0521 ·Ex

−13.1619. This straight line is plotted in black in Fig. 16.11.

For comparison, the standard regression is

E y

= 0.0494x

−5.7871, and it is

plotted in red. Parameter

η was set to 200, and the variances are estimated as

=4852.8 and s

=24.2641.

16.8 Analysis of Covariance

Analysis of covariance (ANCOVA) is a linear model that includes two types of

predictors: quantitative (like the regression) and categorical (like the ANOVA).

It can be formulated in quite general terms, but we will discuss the case of a

single predictor of each kind.

The quantitative variable x is linearly connected with the response, and

for a ﬁxed categorical variable the problem is exactly the regression. On the

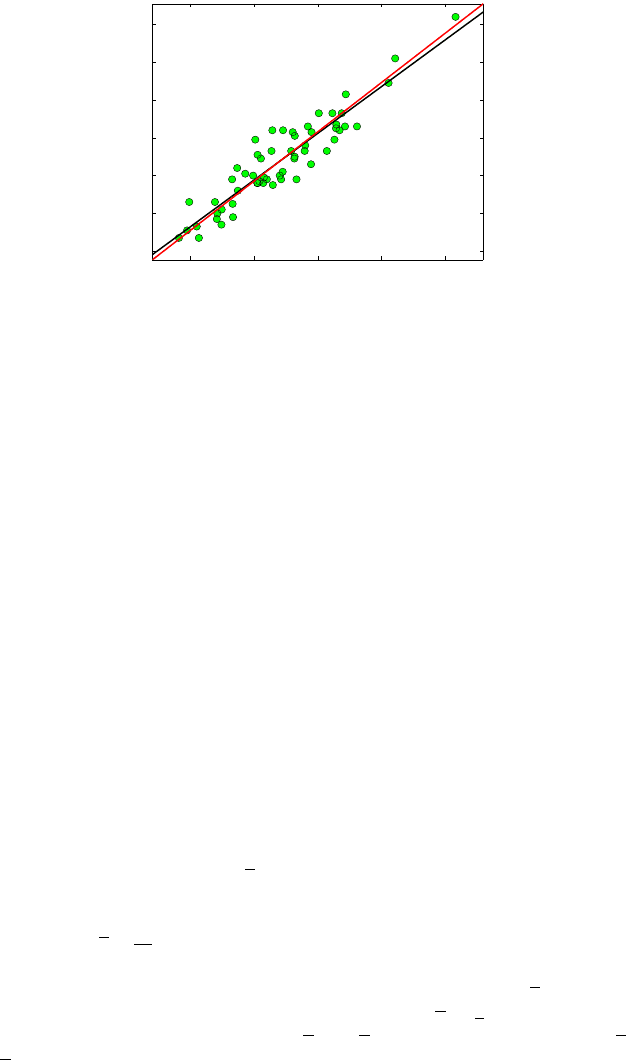
16.8 Analysis of Covariance 639

2000 2500 3000 3500 4000

100

120

140

160

180

200

Plasma Volume

Circulating Albumin

Fig. 16.11 EIV regression (black) and standard regression (red) for circalbumin data.

other hand, for a ﬁxed variable x, the model is ANOVA with treatments/groups

deﬁned by the categorical variable.

The rationale behind the merging of the two models is that in a range

of experiments, modeling the problem as regression only or as ANOVA only

may be inadequate, and that introducing a quantitative covariate to ANOVA,

or equivalently groups/treatments to regression, may better account for the

variability in data and produce better modeling and prediction results.

We will analyze two illustrative examples. In the ﬁrst example, which will

be solved in MATLAB, the efﬁcacies of two drugs for lowering blood pressure

are compared by analyzing the drop in blood pressure after taking the drug.

However, the initial blood pressure measured before the drug is taken should

be taken into account since a drop of 50, for example, is not the same if the

initial pressure was 90 as opposed to 180.

In the second example, which will be solved in WinBUGS, the measured re-

sponse is the strength of synthetic ﬁber and the two covariates are the ﬁber’s

diameter (quantitative) and the machine on which the ﬁber was produced (cat-

egorical with three levels).

We assume the model

i j

=µ +α

+β(x

i j

−x) +²

i j

, i =1, . .., a; j =1,..., n, (16.8)

where a is the number of levels/treatments, n is a common sample size within

each level, and

x =

i, j

i j

is the overall mean of xs. The errors ²

are as-

sumed independent normal with mean 0 and constant variance

For practical reasons the covariates x

i j

are centered as x

i j

− x since the

expressions for the estimators will be more simple. Let

i j

be the ith

treatment mean for the xs. The means

y and y

are deﬁned analogously to x

and

640 16 Regression

In ANCOVA we calculate the sums of squares and mixed-product sums as

i j

−x)

i j

−x)(y

i j

− y)

i j

− y)

−x)

−x)(y

− y)

i j

−x

)

−T

i j

−x

)(y

i j

− y

) = S

−T

i j

− y

)

−T

We are interested in ﬁnding estimators for the parameters in model (16.8),

the common mean

µ, treatment effects α

, regression slope β, and the variance

of the error

The estimators are

µ = y, b =

β =Q

, and

= y

− y −b(x

−x).

The estimator of the variance,

, is s

= MSE =SSE/(a(n −1) −1), where

SSE

−Q

If there are no treatment effects, that is, if all

= 0, then the model is a

plain regression and

i j

=µ +β(x

i j

−x) +²

i j

, i =1, . .., a; j =1,..., n.

In this reduced case the error sum of squares is SSE

= S

−S

, with

−2 degrees of freedom. Thus, the test H

: α

=0 is based on an F-statistic,

(SSE

−SSE)/(a −1)

SSE/(a(n −1) −1)

that has an F-distribution with a

−1 and a(n −1) −1 degrees of freedom.

The test for regression H

: β =0 is based on the statistic

SSE/(a(n −1) −1)

which has an F-distribution with 1 and a(n

−1) −1 degrees of freedom.

Next we provide a MATLAB solution for a simple ANCOVA layout.

Example 16.7. Kodlin (1951) reported an experiment that compared two sub-

stances for lowering blood pressure, denoted as substances A and B. Two

groups of animals are randomized to the two substances and a decrease in

pressure is recorded. The initial pressure is recorded. The data for the blood

pressure experiment appear in the table below. Compare the two substances

by accounting for the possible effect of the initial pressure on the decrease in