Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

16.2 Simple Linear Regression 601

Here β

and β

are the population intercept and slope parameters, respec-

tively, and

is the error. We assume that the errors are not correlated and

have mean 0 and variance

, thus E y

= β

+β

and Var y

= σ

. The goal

is to estimate this linear model, that is, estimate

, β

, and σ

from the

n observed pairs. To put our discussion in context, we consider an example

concerning a study of factors affecting patterns of insulin-dependent diabetes

mellitus in children.

Example 16.1. Diabetes Mellitus in Children. Diabetes mellitus is a con-

dition characterized by hyperglycemia resulting from the body’s inability to

use blood glucose for energy. In type 1 diabetes, the pancreas no longer makes

insulin and therefore blood glucose cannot enter the cells to be used for energy.

The objective was to investigate the dependence of the level of serum C-

peptide on various other factors in order to understand the patterns of resid-

ual insulin secretion. C-peptide is a protein produced by the beta cells of the

pancreas whenever insulin is made. Thus, the level of C-peptide in the blood

is an index of insulin production.

The part of the data from Sockett et al. (1987), discussed in the context

of statistical modeling by Hastie and Tibshirani (1990), is given next. The

response measurement is the logarithm of C-peptide concentration (pmol/ml)

at the time of diagnosis, and the predictor is the base deﬁcit, a measure of

acidity.

Deﬁcit (x) −8.1 −16.1 −0.9 −7.8 −29.0 −19.2 −18.9 −10.6 −2.8 −25.0 −3.1

Log C-peptide (y)

4.8 4.1 5.2 5.5 5 3.4 3.4 4.9 5.6 3.7 3.9

Deﬁcit (x) −7.8 −13.9 −4.5 −11.6 −2.1 −2.0 −9.0 −11.2 −0.2 −6.1 −1

Log C-peptide (y)

4.5 4.8 4.9 3.0 4.6 4.8 5.5 4.5 5.3 4.7 6.6

Deﬁcit (x) −3.6 −8.2 −0.5 −2.0 −1.6 −11.9 −0.7 −1.2 −14.3 −0.8 −16.8

Log C-peptide (y)

5.1 3.9 5.7 5.1 5.2 3.7 4.9 4.8 4.4 5.2 5.1

Deﬁcit (x) −5.1 −9.5 −17.0 −3.3 −0.7 −3.3 −13.6 −1.9 −10.0 −13.5

Log C-peptide (y)

4.6 3.9 5.1 5.1 6.0 4.9 4.1 4.6 4.9 5.1

We will follow this example in MATLAB as an annotated step-by-step

code/output of

cpeptide.m. For more sophisticated analysis, MATLAB has

quite advanced built-in regression tools,

regress, regstats, robustfit, stepwise,

and many other more or less specialized ﬁtting and diagnostic tools.

After importing the data, we specify

p, which is the number of parameters,

rename the variables, and ﬁnd the sample size.

Deficit =[-8.1 -16.1 -0.9 -7.8 -29.0 -19.2 -18.9 -10.6 -2.8...

-25.0 -3.1 -7.8 -13.9 -4.5 -11.6 -2.1 -2.0 -9.0 -11.2 -0.2...

-6.1 -1 -3.6 -8.2 -0.5 -2.0 -1.6 -11.9 -0.7 -1.2 -14.3 -0.8...

-16.8 -5.1 -9.5 -17.0 -3.3 -0.7 -3.3 -13.6 -1.9 -10.0 -13.5];

logCpeptide =[ 4.8 4.1 5.2 5.5 5 3.4 3.4 4.9 5.6 3.7 3.9 ...

4.5 4.8 4.9 3.0 4.6 4.8 5.5 4.5 5.3 4.7 6.6 5.1 3.9 ...

5.7 5.1 5.2 3.7 4.9 4.8 4.4 5.2 5.1 4.6 3.9 5.1 5.1 ...

6.0 4.9 4.1 4.6 4.9 5.1];

602 16 Regression

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

p = 2; %number of parameters, (beta0, beta1)

%"Deficit" measurement is "x", "logCpeptide" is "y".

x = Deficit’ ; %as a column vector

y = logCpeptide’ ; %as a column vector

n = length(x);

It is of interest to express the log C-peptide (variable y) as a linear function

of alkaline deﬁciency (variable x), and the population model y

= β

+β

x +²

is postulated. Finding estimators for β

and β

is an exercise in calculus –

ﬁnding the extrema of a function of two variables. The following derivation is

known as the least-squares method, which is a broad mathematical method-

ology for approximate solutions of overdetermined systems, ﬁrst described by

Gauss at the end of the eighteenth century. The best regression line minimizes

the sum of squares of errors:

i=1

−(β

+β

))

When pairs (x

, y

) are considered ﬁxed, L is a function of β

and β

only.

Minimizing L amounts to solving the so-called normal equations

∂L

∂β

= −2

i=1

−β

] =0 and

∂L

∂β

= −2

i=1

−β

] =0,

that is,

+β

i=1

and

i=1

+β

i=1

. (16.1)

Let

x =

and y =

be the sample means of predictor values

and the responses. If

i=1

−x)(y

− y) =

i=1

−x) =

i=1

−nx y,

i=1

−x)

i=1

−nx

and

16.2 Simple Linear Regression 603

i=1

− y)

i=1

−n y

then the values for

and β

minimizing L or, equivalently, solving the normal

equations (16.1) are

and

= y −

We will simplify the notation by denoting

by b

and

by b

. Thus, the

ﬁtted regression equation is

= b

and b

= y −b

For values x

= x

the ﬁts

are obtained as

= b

with the residuals e

= y

−

. The residuals are the most important diagnostic

modality in regression. They explain how well the predicted data

ﬁt the

observations, and if the ﬁt is not good, residuals indicate what caused the

problem.

%Sums of Squares

SXX = sum( (x - mean(x)).^2 ) %SXX=2.1310e+003

SYY = sum( (y - mean(y)).^2 ) %SYY=21.807

SXY = sum( (x - mean(x)).

(y - mean(y)) ) %SXY=105.3477

%estimators of coefficients beta1 and beta0

b1 = SXY/SXX %0.0494

b0 = mean(y) - b1

mean(x) %5.1494

% predictions

yhat = b0 + b1

%residuals

res = y - yhat;

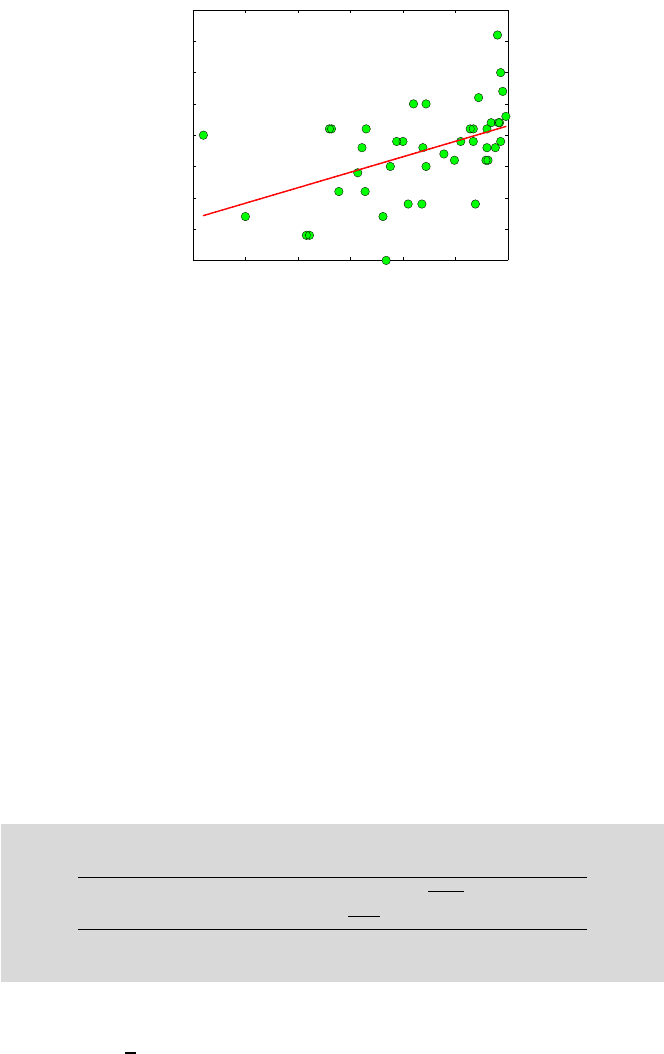
We found that yhat=5.1494+0.0494

x. Figure 16.2 shows scatterplot of log

C-peptide level (y) against alkaline deﬁciency (x) with superimposed regres-

sion ﬁt b

Denote by SSE the sum of squared residuals, SSE

One can show that SSE

= S

−b

and that E(SSE) = (n −2)σ

. Thus,

the mean square error MSE

= SSE/(n −2) is an unbiased estimator of error

variance

. Recall the fundamental ANOVA identity SST =SST r +SSE. In

regression terms, the fundamental ANOVA identity has the form

604 16 Regression

−30 −25 −20 −15 −10 −5 0

3.5

4.5

5.5

6.5

Alcaline Defficiency

C−Peptide Level (log units)

Fig. 16.2 Scatterplot of log C-peptide level (y) against alkaline deﬁciency (x). The regression

ﬁt (red) is

=5.1494 +0.0494x.

SST =SSR +SSE,

where SST

, SSR = b

, and SSE =

. Since

ESSR =σ

+β

SSR has an associated 1 degree of freedom and the regression mean sum of

squares MSR is SSR/1

=SSR.

The statistic MSR becomes an unbiased estimator of variance

when

= 0. Thus, to test H

: β

= 0 one should have F = MSR/MSE close to 1

since under H

both MSR and MSE estimate the same quantity, σ

. Under

, the statistic F = MSR/MSE has an F-distribution with 1 and n−2 degrees

of freedom.

Large values of F indicate that there is a contribution of

in MSR and

discrepancy from H

can be assessed using an F-test. The sums of squares,

degrees of freedom, mean squares, F-statistic and p-value associated with ob-

served F are customarily summarized in an ANOVA table:

Source DF SS MS F p-value

Regression 1 SSR MSR =SSR F =

MSR

MSE

P(F

1,n−2

>F)

Error n

−2 SSE MSE =

SSE

n−2

Total n −1 SST

The p-value is associated with testing of H

, which essentially states that

covariate x does not inﬂuence the response y and the same ﬁt can be obtained

by just taking

y as the model for y

16.2 Simple Linear Regression 605

%ANOVA Identity

SST = sum((y - mean(y)).^2) %this is also SYY

SSR = sum((yhat - mean(y)).^2) %5.2079

SSE = sum((y - yhat).^2) %=sum(res.^2), 16.599

% forming F and testing the adequacy of linear regression

MSR = SSR/(p - 1) %5.2079

MSE = SSE/(n - p) %estimator of variance, 0.4049

s = sqrt(MSE) %0.6363

F = MSR/MSE %12.8637

pvalue = 1-fcdf(F, p-1, n-p)

%testing H

0: regression has beta1=0,

%that is, there is no need for linear fit, p-val = 0.00088412

The above calculations are arranged in the ANOVA table:

Source DF SS MS F p-value

Regression 1 5.2079 5.2079 12.8637 0.0009

Error 41 16.5990 0.4049

Total 42 21.8070

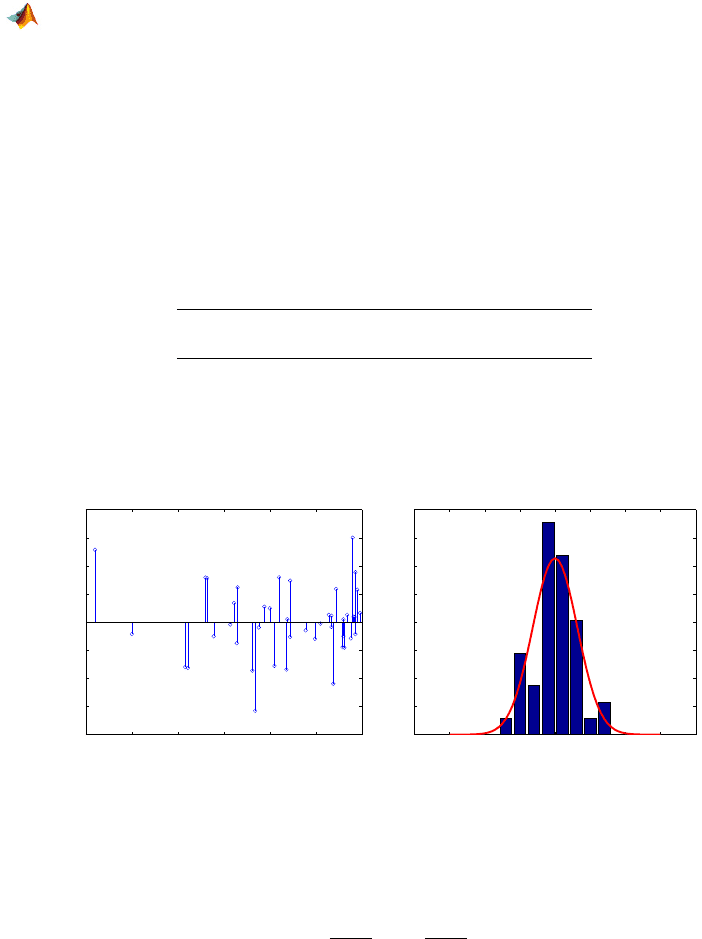
Figure 16.3a shows plot of residuals y

−

against x

. A normalized his-

togram of residuals with superimposed normal distribution

N (0,0.6363

), is

given in Fig. 16.3b.

−30 −25 −20 −15 −10 −5 0

−2

−1.5

−1

−0.5

0.5

1.5

−4 −3 −2 −1 0 1 2 3 4

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

(a) (b)

Fig. 16.3 (a) Plot of residuals y

−

against x. (b) Normalized histogram of residuals with

superimposed normal distribution

N (0, s

), with s estimated as 0.6363.

The quantity R

, called the coefﬁcient of determination, is deﬁned as

SSR

SST

=1 −

SSE

SST

The R

in this context coincides with the square of the correlation coefﬁcient

between (x

,... , x

) and (y

,... , y

). However, the representation of R

via the

ratio SSR/SST is more illuminating. In words, R

explains what proportion

606 16 Regression

of the total variability (SST) encountered in observations is explained or ac-

counted for by the regression (SSR). Thus, a high R

is desirable in any re-

gression. The adjusted R

is deﬁned as

ad j

=1 −

n −1

n − p

SSE

SST

but it is important only in cases with many predictors (p

>2) since it penalizes

inclusion of predictors in the model.

% Other measures of goodness of fit

R2 = SSR/SST %0.2388

R2adj = 1 - (n-1)/(n-p)

SSE/SST %0.2203

Often, instead of regressing y

on x

, one regresses y

on x

−x as

=β

∗

+β

−x).

This is beneﬁcial for several reasons. In practice, we calculate only the es-

timator b

. Since the ﬁtted line contains the point (x, y), the intercept β

∗

estimated by

y, and our regression ﬁt is

= y +b

−x).

In the Bayesian context estimating

∗

and β

is more stable and efﬁcient

than estimating

and β

directly since y and b

are uncorrelated.



Estimators b

and b

are unbiased estimators of population’s β

and β

We will show that they are unbiased and that their variance is intimately

connected with the variance of responses,

= β

and Var b

= β

and Var b

=σ

(x)

Here is the rationale:

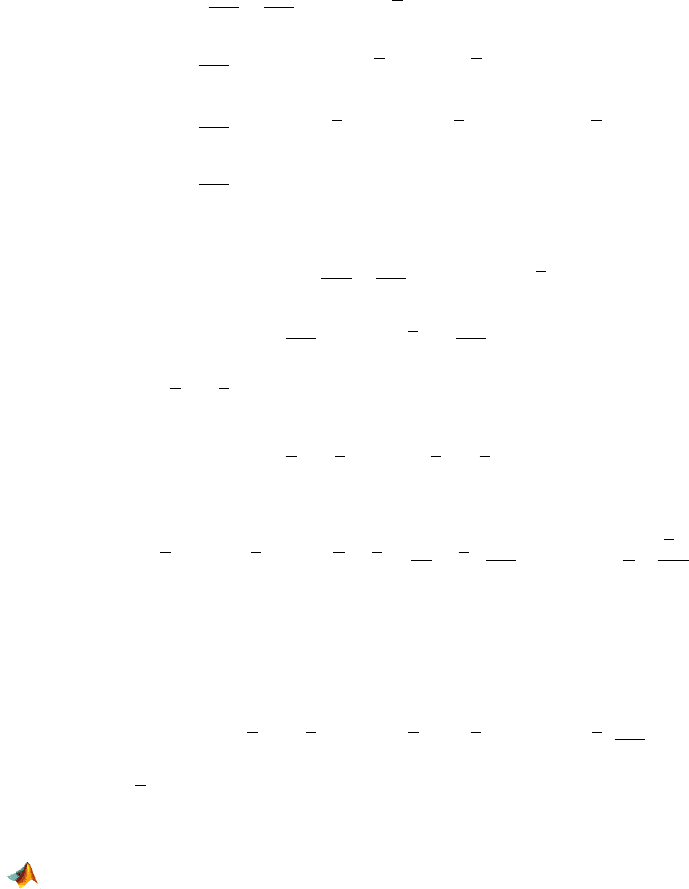
16.2 Simple Linear Regression 607

= E

i=1

−x)

i=1

(β

∗

+β

−x) +²

)(x

−x)

i=1

∗

−x) +

i=1

−x)

i=1

−x)

0 +β

Var b

= Var

i=1

Var (y

−x))

i=1

−x)

Since b

= y −b

=E(y −b

x) =β

+β

x −β

x =β

and

Var b

=Var y +Var (b

x) −2Cov(y, b

x) =

+(x)

−2 ·0 =σ

(x)

Sample counterparts of

Var b

and Var b

will be needed for the inference

in subsequent sections, they are obtained by plugging in the MSE in place of

The covariance between b

and b

Cov(b

, b

) =Cov(y −b

·x, b

) =Cov(y, b

) −x ·Var (b

) =−x ·

since

Cov(y, b

) =0.

In MATLAB the estimator of

σ and sample standard deviations of estima-

tors b

and b

from Example 16.1 are as follows:

% s, sb0, and sb1

s = sqrt(MSE) %s = 0.6363

%Standard errors of parameter estimators

sb1 = s/sqrt(SXX) %sb1 = 0.0138

sb0 = s

sqrt(1/n + (mean(x))^2/SXX ) %sb0 = 0.1484

608 16 Regression

16.2.1 Testing Hypotheses in Linear Regression

To ﬁnd the estimators of regression parameters and calculate their expecta-

tions and variances we do not need distributional properties of errors – except

that they are independent, have a mean 0 and a variance that does not vary

with x. However, to test the hypotheses about the population intercept and

slope, and to ﬁnd conﬁdence intervals, we need to assume that the errors

are

i.i.d. normal. In practice, the residual analysis is conducted to verify whether

the normality assumption is justiﬁed.

16.2.1.1 Inference About the Slope Parameter

For a given constant β

, the test for

: β

=β

relies on the statistic

−β

where s

= MSE. This statistic under H

has a t-distribution with n −2 de-

grees of freedom, and testing is done as follows:

Alternative α-level rejection region p-value (MATLAB)

: β

>β

n−2,1−α

,∞) 1-tcdf(t,n-2)

: β

6=β

(−∞, t

n−2,α/2

] ∪[t

n−2,1−α/2

,∞) 2

tcdf(-abs(t),n-2)

: β

<β

(−∞, t

n−2,α

] tcdf(t,n-2)

The distribution of the test statistic is derived from a linear representation

of b

i=1

, a

−x

Under H

, b

∼N (β

,σ

). Thus,

−β

SSE

(n−2)σ

16.2 Simple Linear Regression 609

which by deﬁnition has a t

n−2

distribution, as Z/

−2

n−2

. We also used the fact

that s

= MSE =SSE/(n −2).

The (1 −α)100% conﬁdence interval for β

−t

n−2,1−α/2

, b

n−2,1−α/2

16.2.1.2 Inference About the Intercept Parameter

For a given constant β

, the test for

: β

=β

relies on the statistic

−β

(x)

Under H

this statistic has a t-distribution with n −2 degrees of freedom and

testing is done as follows:

Alternative α-level rejection region p-value (MATLAB)

: β

>β

n−2,1−α

,∞) 1-tcdf(t,n-2)

: β

6=β

(−∞, t

n−2,α/2

] ∪[t

n−2,1−α/2

,∞) 2

tcdf(-abs(t),n-2)

: β

<β

(−∞, t

n−2,α

] tcdf(t,n-2)

This is based on the representation of b

as b

= y − b

x and under H

∼N

,σ

(x)

´´

. Thus,

−β

1/n +(x)

−β

1/n +(x)

−β

1/n+(x)

SSE

(n−2)σ

which by deﬁnition has a t

n−2

distribution, as Z/

−2

n−2

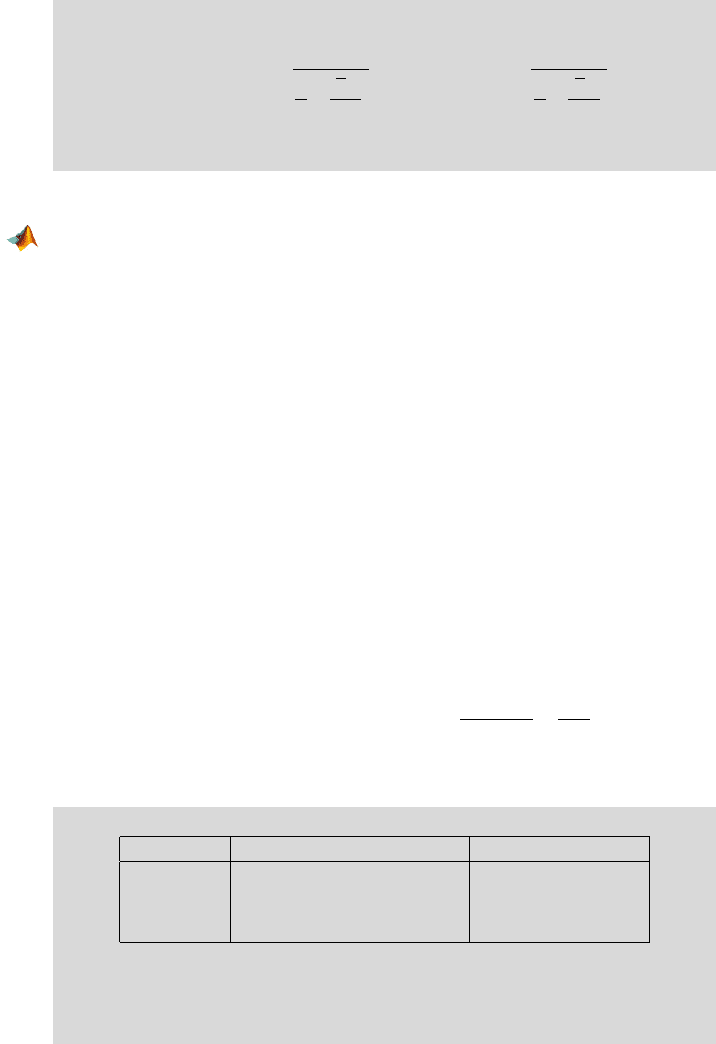
610 16 Regression

The (1 −α)100% conﬁdence interval for β

−t

n−2,1−α/2

(x)

, b

n−2,1−α/2

(x)

% are the coefficients equal to 0?

t1 = b1/sb1 %3.5866

pb1 = 2

(1-tcdf(abs(t1),n-p) ) %8.8412e-004

t0 = b0/sb0 %34.6927

pb1 = 2

(1-tcdf(abs(t0),n-p) ) %0

%test H

0: beta1 = 0.04 vs H

1: beta1 > 0.04

tst1 = (b1 - 0.04)/sb1 %0.6846

ptst1 = 1 - tcdf( tst1, n-p ) %0.2487

% test H

0: beta0 = 5.8 vs H

1: beta0 < 5.8

tst2 = (b0 - 5.8)/sb0 %-4.3836

ptst2 = tcdf(tst2, n-p ) %3.9668e-005

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% Find 95% CI for beta1

[b1 - tinv(0.975, n-p)

sb1, b1 + tinv(0.975, n-p)

sb1]

% 0.0216 0.0773

% Find 99% CI for beta0

[b0 - tinv(0.995, n-p)

sb0, b0 + tinv(0.995, n-p)

sb0]

% 4.7484 5.5503

16.2.1.3 Inference About the Variance σ

Testing H

: σ

=σ

relies on the statistic χ

(n−2)MSE

SSE

. This statistic

under H

has a χ

-distribution with n −2 degrees of freedom and testing is

done as follows:

Alternative α-level rejection region p-value (MATLAB)

: σ

<σ

[0,χ

−2,α

] chi2cdf(chi2,n-2)

: σ

6=σ

[0,χ

−2,α/2

] ∪[χ

−2,1−α/2

,∞) 2

chi2cdf(ch,n-2)

: σ

>σ

[χ

−2,1−α

,∞) 1-chi2cdf(chi2,n-2)

where chi2 is the test statistic and ch=min(chi2,1/chi2).

The (1

−α)100% conﬁdence interval for σ