Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

17.2 Logistic Regression 661

data in this example comes from Munich’s Klinikum Großharden (Fahrmeir

and Tutz, 1996) and concerns infections in births by C-section. The response

variable of interest is the occurrence or nonoccurrence of infection. Three co-

variates, each at two levels, were considered as important for the occurrence

of infection:

noplan – The C-section delivery was planned (0) or not planned (1);

riskfac – Risk factors for the mother, such as diabetes, overweight, previ-

ous C-section birth, etc., are present (1) or not present (0); and

antibio – Antibiotics as a prophylaxis are given (1) or not given (0).

Table 17.1 provides the results.

Table 17.1 Caesarean-section delivery data.

Planned No Plan

Infection Infection

yes no total yes no total

Antibiotics

Risk factor yes 1 17 18 11 87 98

Risk factor no 0 2 2 0 0 0

No Antibiotics

Risk factor yes 28 30 58 23 3 26

Risk factor no 8 32 40 0 9 9

Here is the MATLAB code that uses built-in functions glmfit and glmval

to ﬁt and present the model.

infection = [ 1 11 0 0 28 23 8 0];

total = [18 98 2 0 58 26 40 9];

proportion = infection./total;

noplan = [ 0 1 0 1 0 1 0 1];

riskfac = [ 1 1 0 0 1 1 0 0];

antibio = [ 1 1 1 1 0 0 0 0];

[b,dev,stats] = glmfit([noplan’ riskfac’ antibio’],...

[infection’ total’],’binomial’,’logit’);

logitFit = ...

glmval(b,[noplan’ riskfac’ antibio’],’logit’);

The resulting additive model (no interactions) is

log

P(infection)

P(no infection)

=β

+β

·noplan +β

·riskfac +β

·antibio

with estimators of

βs as

–1.8926 1.0720 2.0299 –3.2544

The interpretation of the estimators for β coefﬁcients is illuminating if we

look at the odds ratio

P(infection)

P(no infection)

662 17 Regression for Binary and Count Data

P(infection)

P(no infection)

=exp(β

) ·exp(β

noplan) ·exp(β

riskfac) ·exp(β

antibio).

For example, when

antibio=1, i.e., when antibiotics are given, the estimated

odds of infection

P(infection)/P(no infection) increase by the factor exp(−3.25) =

0.0388, that is, the odds decrease 25.79 times. Of course, these statements are

valid only if the model is accurate. Other competing models (such as probit or

clog-log) may result in different changes in risk ratios.

1 2 3 4 5 6 7 8

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Code for (noplan, riskfact, antibio)

Probability of Infection

Observed Proportions

Logistic Fit

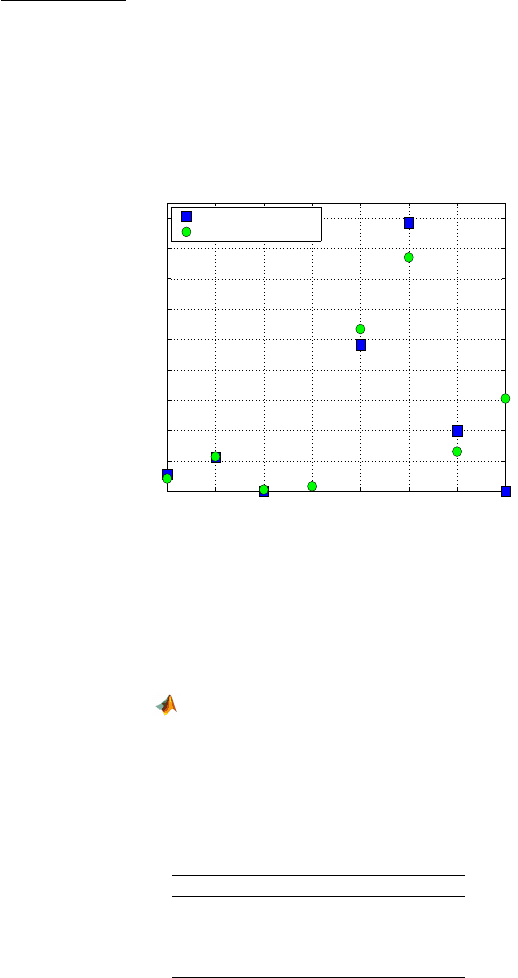
Fig. 17.1 Caesarean delivery infection predictions. For a triple (noplan, riskfac, antibio), the

numbers on the x-axis code as follows: 1=(0,1,1), 2=(1,1,1), 3=(0,0,1), 4=(1,0,1), 5=(0,1,0),

6=(1,1,0), 7=(0,0,0), and 8=(1,0,0). Blue squares are the observed relative frequencies and

green circles are the model-predicted probabilities of infection. Note that point 4 does not

have an observed proportion.

The m-function logisticmle.m also gives standard errors for estimators

βs. Table provides t-values, that is, ratios of coefﬁcients and their stan-

dard deviations, for testing if the coefﬁcients are signiﬁcantly different from

0. These are known as Wald’s Z statistics, since they are approximately nor-

mal.

Table 17.2 t-ratios (Wald’s Z statistic) for the estimators b =

β.

b s

Intercept –1.8926 0.4124 –4.5893

noplan 1.0720 0.4253 2.5203

riskfac 2.0299 0.4553 4.4588

antibio –3.2544 0.4812 –6.7624

The deviance (p. 665) of this model as a measure of goodness of ﬁt is dis-

tributed as

with 3 degrees of freedom. The number of degrees of freedom is

17.2 Logistic Regression 663

calculated as 7 (number of groups with observations) minus 4 (four estimated

parameters

−β

). Since it is found to be signiﬁcant,

dev = 10.9967;

pval = 1 - chi2cdf(dev, 7-4) % 0.0117

the ﬁt of this model is not good. To improve the ﬁt, one may include the inter-

actions.

One may ask why the regression model was needed in the ﬁrst place.

The probabilities of interest could be predicted by relative frequencies. For

example, in the case (

noplan = 0, riskfac = 1, antibio = 1), the relative fre-

quency of infection was 1/18

= 0.0556, just slightly larger than the model-

predicted

=0.0424. There are two beneﬁts to this approach. First, the model

is able to predict probabilities in the cases where no patients are present, such

as for (

noplan = 1, riskfac = 0, antibio = 1). Second, the predictions for the

cases where y

= 1 is not observed are “borrowing strength” from the model

and are not modeled individually. For example, zero as an estimator in the

case (

noplan = 1, riskfac = 0, antibio = 0) is not reasonable; the model-based

estimator

= 0.3056 is more realistic. Figure 17.1 compares observed and

model-predicted infection rates. For a triple of covariates (noplan, riskfac, an-

tibio), the numbers on the x-axis code as follows: 1=(0,1,1), 2=(1,1,1), 3=(0,0,1),

4=(1,0,1), 5=(0,1,0), 6=(1,1,0), 7=(0,0,0), and 8=(1,0,0). Note that point 4 does

not have an observed proportion, however the model-predicted proportion can

be found. For computational aspects refer to ﬁle

caesarean.m.

Next, we provide a Bayesian solution to this example and compare the

model ﬁt with the classical ﬁt above. The comparisons are summarized in Ta-

ble 17.1.

C-SECTION INFECTIONS

model{

for(i in 1:N){

inf[i] ~ dbin(p[i],total[i])

logit(p[i]) <- beta0 + beta1

noplan[i] +

beta2

riskfac[i] + beta3

antibio[i]

}

beta0 ~dnorm(0, 0.00001)

beta1 ~dnorm(0, 0.00001)

beta2 ~dnorm(0, 0.00001)

beta3 ~dnorm(0, 0.00001)

}

DATA

list(inf=c(1, 11, 0, 0, 28, 23, 8, 0),

total = c(18, 98, 2, 0, 58, 26, 40, 9),

noplan = c(0,1,0,1,0,1,0,1),

riskfac = c(1,1, 0, 0, 1,1, 0, 0),

antibio =c(1,1,1,1,0,0,0,0), N=8)

664 17 Regression for Binary and Count Data

INITS

list(beta0 =0, beta1=0, beta2=0, beta3=0)

mean sd MC error val2.5pc median val97.5pc start sample

beta0 –1.964 0.4258 0.001468 –2.853 –1.945 –1.183 1001 1000000

beta1 1.111 0.4339 8.857E-4 0.2851 1.102 1.986 1001 1000000

beta2 2.104 0.4681 0.00159 1.226 2.09 3.066 1001 1000000

beta3 –3.335 0.4915 9.756E-4 –4.337 –3.322 –2.411 1001 1000000

deviance 32.24 2.873 0.00566 28.67 31.59 39.49 1001 1000000

Table 17.3 Comparison of classical and noninformative Bayes estimators b =

β, with esti-

mators of standard deviations.

b s

Intercept −1.8926 0.4124 −1.964 0.4258

noplan 1.0720 0.4253

1.111 0.4339

riskfac 2.0299 0.4553

2.104 0.4681

antibio

−3.2544 0.4812 −3.335 0.4915

17.2.2 Assessing the Logistic Regression Fit

The measures for assessing the goodness of linear regression ﬁt that we cov-

ered in Chap. 16, R

, F, MSE, etc., are not appropriate for logistic regression.

As in the case of linear regression, there is a range of measures for assessing

the performance of logistic regression and we will brieﬂy overview a few.

The signiﬁcance of model parameters

,β

,... is tested by the so-called

Wald’s test. One ﬁnds the statistic Z

s(b

)

that has an approximate normal

distribution if the coefﬁcient

is 0. Equivalently, W

)

with an approx-

imate

-distribution with 1 degree of freedom can be used. Large values of

| or W

are critical for H

: β

=0.

The sample variances s

) are diagonal elements of (X

V X )

−1

, where







1 x

... x

1,p−1

1 x

... x

2,p−1

...

1 x

... x

n,p−1







is the design matrix and

17.2 Logistic Regression 665

V =







(1 −

) 0 ... 0

(1 −

) ... 0

...

0 0 ...

(1 −

)







The customary measure for goodness of ﬁt is deviance, deﬁned as

=−2log

likelihood of the ﬁtted model

likelihood of the saturated model

For the logistic regression in (17.2), where y

is the number of 1s and n

−y

the number of 0s in class i, the likelihood is L

(1 − p

)

−y

and the

deviance is

=−2

1=1

log

− y

)log

−

− y

¶¾

where

= n

is the model ﬁt for y

. The saturated model estimates p

= y

and

= y

providing the ﬁt that matches the observations.

The deviance statistic in this case has a

-distribution with k − p degrees

of freedom, where k is the number of classes/groups and p is the number of

parameters in the model. Recall that in the previous example the deviance of

the model was distributed as

with k − p =7 −4 =3 degrees of freedom.

For both Bernoulli and binomial observations, the mean and variance de-

pend on a single parameter, p. When the mean is well ﬁtted, the variance

could be underﬁtted (overdispersion in data) or overﬁtted (underdispersion in

data). The ratio D/df is often used to indicate over- or underdispersion in the

data.

The traditional

-statistic for the goodness of ﬁt in model (17.2) is deﬁned

i=1

−

)

−

)

−

where n

is the number of observations in class i, i =1, . .., k. This statistic has

an approx.

-distribution with k − p degrees of freedom.

Goodness of ﬁt measure G is deﬁned as the difference of deviance between

the null model (intercept-only model) and the model under consideration. G

has a

-distribution with p −1 degrees of freedom, and small values of G are

critical, suggesting that the deviance did not improve signiﬁcantly by adding

covariates.

The logistic model can always be expressed in terms of Bernoulli outcomes,

where y

is 0 or 1, as in (17.1). Then k = n, n

= 1, the likelihood for the sat-

urated model, is

(1 − y

)

1−y

= 1 (we assume that 0

= 1), and the de-

viance for the Bernoulli representation becomes

666 17 Regression for Binary and Count Data

D =−2

i=1

[

log

+(1 − y

)log(1 −

)

]

Statistic D does not follow any speciﬁc distribution, irrespective of sample

size. Likewise, the Pearson

becomes

i=1

−

)

(1 −

)

(17.3)

in model (17.1) and does not follow any speciﬁc distribution, either.

To further evaluate the model, several types of residuals are available.

Deviance residuals are deﬁned as

=sign(y

−

)

log

− y

)log

− y

−

¶¾

, i =1, . .., k,

for model (17.2) and

=sign(y

−

)

log

+(1 − y

)log(1 −

), i =1, . .., n,

for model (17.1). The deviance D is decomposed to the sum of squares of de-

viance residuals in an ANOVA-like fashion as D

)

. The squared resid-

ual (r

)

measures the contribution of the ith case to the deviance.

Deviance residuals can be plotted against the order of sampling to explore

for possible trends and outliers. Also useful for checking the model are half-

normal plots where the ordered absolute values r

are plotted against the

normal quantiles

−1

i+n−1/8

2n+1/2

. These kinds of plots are an extension of Atkin-

son’s (1985) half normal plots in regular linear regression models. Deviation

from a straight line in a half-normal plot indicates model inadequacy.

For the model in (17.1), the Pearson residual is deﬁned as

pea

−

(1 −

)

and the sum of squares of r

pea

constitutes Pearson’s χ

statistic,

i=1

pea

)

i=1

−

)

(1 −

)

as in (17.3). This statistic represents a discrepancy measure; however, as we

mentioned, it does not follow the

-distribution, even asymptotically.

In the case of continuous covariates, large n and small n

, Hosmer and

Lemeshow proposed a

-statistic based on the grouping of predicted values

. All

are ordered and divided into g approximately equal groups, usually

ten. For ten groups, sample deciles of ordered

could be used.

The Hosmer–Lemeshow statistic is

17.2 Logistic Regression 667

i=1

−n p

)

where g is the number of groups, n

is the number of cases in the ith group,

and

is the average of model (predicted) probabilities for the cases in the

ith group. The

-statistic is compared to χ

−2

quantiles, and small p-values

indicate that the ﬁt is poor. In the case of ties, that is, when there are blocks

of items with the same predicted probability

p, the blocks are not split but

assigned to one of the two groups that share the block. The details of the algo-

rithm can be found in Hosmer and Lemeshow (1989).

In the case of linear regression, R

, as a proportion of model-explained

variability in observations, had a strong intuitive appeal in assessing the re-

gression ﬁt. In the case of logistic regression, there is no such intuitive R

However, there are several proposals of R

-like measures, called pseudo-R

Most of them are deﬁned in terms of model likelihood or log-likelihood. The

model likelihood and log-likelihood are calculated using model logit,

= b

+···+b

p−1

i,p−1

= LL(b

,... , b

p−1

) =

i=1

(

×`

−log(1 +exp{`

})

)

and the model likelihood is L

= exp{LL

}. The null model is ﬁtted without

covariates, and

= b

null

= LL(b

) =

i=1

(

×`

−log(1 +exp{`

})

)

The null model likelihood is L

null

=exp{LL

null

By analogy to linear regression, R

SSR

SST

SST−SSE

SST

m f

null

−LL

null

=1 −

null

deﬁnes McFadden’s pseudo-R

. Some other counterparts of R

are

Cox–Snell: R

= 1 −

null

2/n

;

Nagelkerke: R

1 −

null

2/n

1 −

(

null

)

2/n

;

Effron: R

= 1 −

−

)

− y)

, y =

668 17 Regression for Binary and Count Data

Example 17.2. Arrhythmia. Patients who undergo coronary artery bypass

graft surgery (CABG) have an approximately 19 to 40% chance of developing

atrial ﬁbrillation (AF). AF is a quivering, chaotic motion in the upper cham-

bers of the heart, known as the atria. AF can lead to the formation of blood

clots, causing greater in-hospital mortality, strokes, and longer hospital stays.

While this can be prevented with drugs, it is very expensive and sometimes

dangerous if not warranted. Ideally, several risk factors that would indicate an

increased risk of developing AF in this population could save lives and money

by indicating which patients need pharmacological intervention. Researchers

began collecting data from CABG patients during their hospital stay such as

demographics like age and sex, as well as heart rate, cholesterol, operation

time, etc. Then the researchers recorded which patients developed AF during

their hospital stay. The goal was to evaluate the probability of AF given the

measured demographic and risk factors.

The data set

arrhythmia.dat, courtesy of Dr. Matthew C. Wiggins, con-

tains the following variables:

Y Fibrillation

Age

Aortic Cross Clamp Time

Cardiopulmonary Bypass Time

Intensive Care Unit (ICU) Time

Average Heart Rate

Left Ventricle Ejection Fraction

Anamnesis of Hypertension

Gender [1 - Female; 0 - Male]

Anamnesis of Diabetes

Previous MI

The MATLAB script arrhythmia.m provided a logistic regression ﬁt. The

script calculates deviance and several goodness-of-ﬁt measures.

load ’Arrhythmia.mat’

Y = Arrhythmia(:,1);

X = Arrhythmia(:,2:11); %Design matrix n x (p-1) without

%vector 1 (intercept)

Xdes =[ones(size(Y)) X]; %with the intercept: n x p

n = length(Y); %number of subjects

alpha = 0.05; %alpha for CIs

[b, dev, stats]=glmfit(X,Y, ’binomial’,’link’,’logit’)

lin = Xdes

b %linear predictor, n x 1 vector

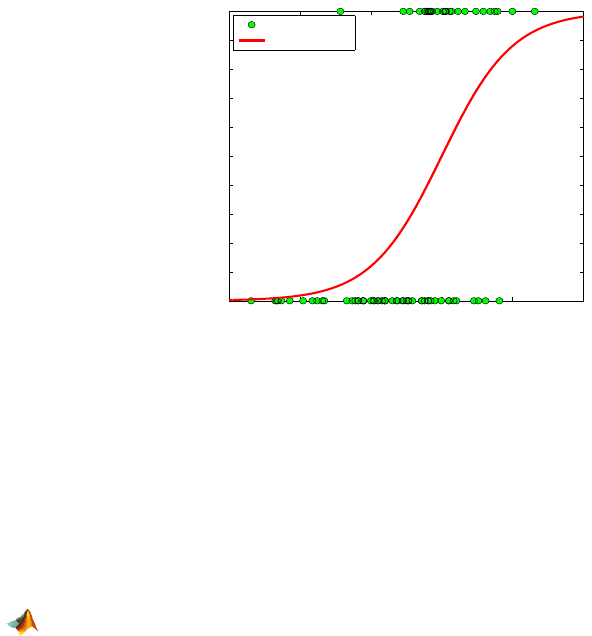
Figure 17.2 shows observed arrhythmia responses (0 or 1) with their logis-

tic ﬁt.

With the linear predictor, ﬁtted probabilities for

= 1} are given as

Also, the estimators of the

βs and their standard deviations and p-values for

17.2 Logistic Regression 669

−6 −4 −2 0 2 4

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Linear Predictor: b

+ b

+ ... + b

Probability of Arrhythmia

Observations

Logistic Fit

Fig. 17.2 Arrhythmia responses 0 or 1 with their logistic ﬁt. The abscise axis is the linear

predictor

lin.

the Wald test are given next. The intercept is signiﬁcantly nonzero (0.0158),

and the variable

X1 (age) is strongly signiﬁcant (0.0005). This agrees with the

inference based on conﬁdence intervals, only the intervals for

and β

do not

contain 0, or, equivalently, the intervals for the odds ratio, exp

{β

} and exp{β

do not contain 1.

phat = exp(lin)./(1 + exp(lin));

V = diag( phat .

(1 - phat) );

sqrtV = diag( sqrt(phat .

(1 - phat) ))

sb = sqrt( diag( inv( Xdes’

Xdes ) ) )

% inv( Xdes’

Xdes ) is stats.covb

% Wald tests for parameters beta

z = b./sb %tests for beta

i = 0, i=0,...,p-1

pvals = 2

normcdf(-abs(z)) %p-values

%[0.0158; 0.0005; 0.3007; 0.2803; 0.1347; 0.8061

% 0.4217; 0.3810; 0.6762; 0.0842; 0.5942]

%(1-alpha)

100% CI for betas

CIs = [b - norminv(1 - alpha/2)

sb , b + norminv(1-alpha/2)

sb]

%(1-alpha)

100% CIs for odds ratios

CIsOR = exp([b-norminv(1-alpha/2)

sb , b+norminv(1-alpha/2)

sb])

% 0.0000 0.1281

% 1.0697 1.2711

% 0.9781 1.0744

% ...

% 0.8628 10.3273

% 0.4004 4.9453

Figure 17.3 shows estimators of β

−β

(as green circles) and 95% con-

ﬁdence bounds. Since the intervals for

and β

do not contain 0, both the

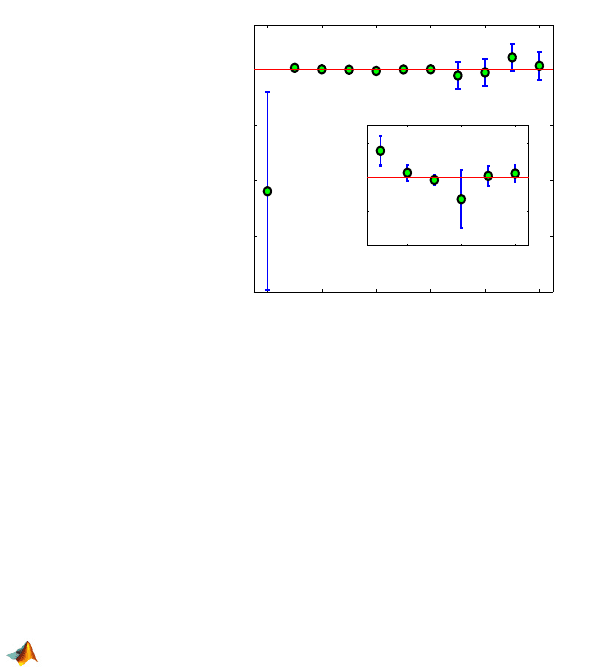
670 17 Regression for Binary and Count Data

intercept and covariate age are important in the model. It is tempting to do

variable/model selection based on outcomes of Wald’s test – but this is not

advisable. Exclusion of a parameter/variable from the model will necessarily

change the estimators and conﬁdence intervals for the remaining parameters

and previously insigniﬁcant parameters may become signiﬁcant. As in linear

regression, best subset, forward, and backward variable selection procedures

exist and may be implemented.

0 2 4 6 8 10

−20

−15

−10

−5

index

b ±1.96s

2 4 6

−0.4

−0.2

0.2

index

b ±1.96s

Fig. 17.3 Estimators of β

−β

are shown as green circles, and 95% conﬁdence intervals

are given. For comparison, the intervals for

−β

are shown separately on a different scale.

Next, we ﬁnd the log-likelihoods for the model and null model. The model

deviance is 78.2515, while the difference of deviances between the models is

26.1949. This would be a basis for a likelihood ratio test if the response were

grouped. Since in a Bernoulli setup the distributions of deviance and G are

not

, the testing needs to be done by one of the response-grouping methods,

such as the Hosmer–Lemeshaw method.

%Log-likelihood

loglik = sum( Y .

lin - log( 1 + exp(lin) )) %-39.1258

%fitting null model.

[b0, dev0, stats0] = glmfit(zeros(size(Y)),Y,’binomial’,’link’,’logit’)

%b0=-0.6381, dev0=104.4464, stats=... (structure)

loglik0 = sum( Y .

b0(1) - log(1 + exp(b0(1))) ) %-52.2232

G = -2

(loglik0 - loglik) % 26.1949

dev0 - dev %26.1949, the same as G, difference of deviances

%model deviance

devi = -2

sum( Y .

log( phat + eps) + (1-Y ).

log(1 - phat + eps) )