Верба В.С. Авиационные комплексы радиолокационного дозора и наведения. Состояние и тенденции развития. 2008

Подождите немного. Документ загружается.

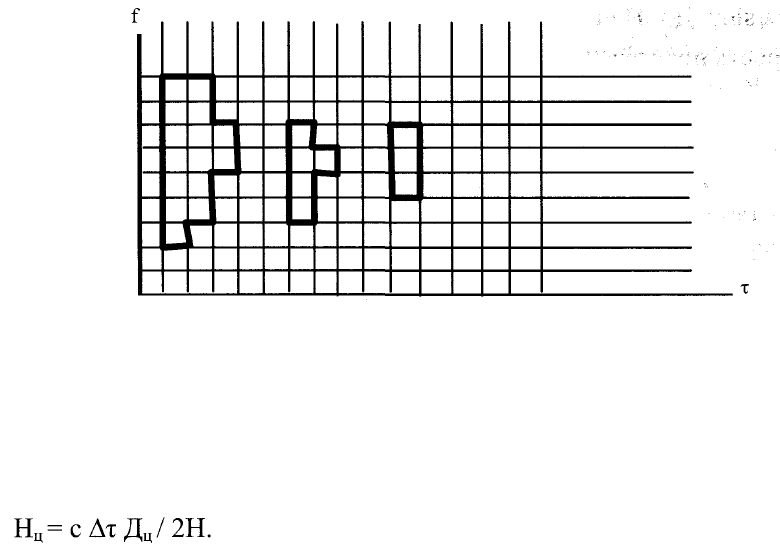
Рис. 3.1

ляется по формуле Δτ = 2Н

Η / Д

, где Н

, Η - высота цели и высота РЛС, Д

дальность до цели.

При наличии отметки антипода возможно измерение высоты цели путем

измерения разницы задержек отметок цели и антипода Δτ:

Такой метод используется в комплексе корабельного базирования Е-2

(Хокай) при обнаружении низколетящих целей на фоне отражений от морской

поверхности. Однако точность измерения высоты цели на больших дальностях

невелика.

При отсутствии отметок антипода измерение высоты цели осуществляется

при помощи ДН антенны в угломестной плоскости. Однако широкая ДН ан-

тенны (5-6°) не обеспечивает высокую точность измерения высоты цели, нахо-

дящейся на больших дальностях.

Кроме сигналов целей могут быть обнаружены сигналы помех от подсти-

лающей поверхности. Помехи, принятые по главному лучу, обычно подавля-

ются на этапе когерентной обработки. Проводится режекция области частот,

занятой этой помехой, и бланкирование обнаружения в соответствующих час-

тотных каналах. Вследствие того, что антенна РЛС, установленная на воздуш-

ном носителе, имеет сравнительно малые размеры по высоте, угломестная диа-

грамма направленности обладает значительным уровнем боковых лепестков во

всей полусфере. Это создает условия для формирования так называемых «вы-

сотных» или альтиметровых отражений от местности, находящейся непосред-

ственно под самолетом-носителем РЛС. Эти сигналы концентрируются в низ-

кочастотной области доплеровского спектра частот, а их протяженность по

дальности определяется шириной диаграммы обратного рассеяния подстилаю-

щей поверхности. Рис. 3.2 поясняет соотношения между параметрами альти-

метрового сигнала.

Связь между частотой сигнала и геометрическим положением отражателя

выражается зависимостью

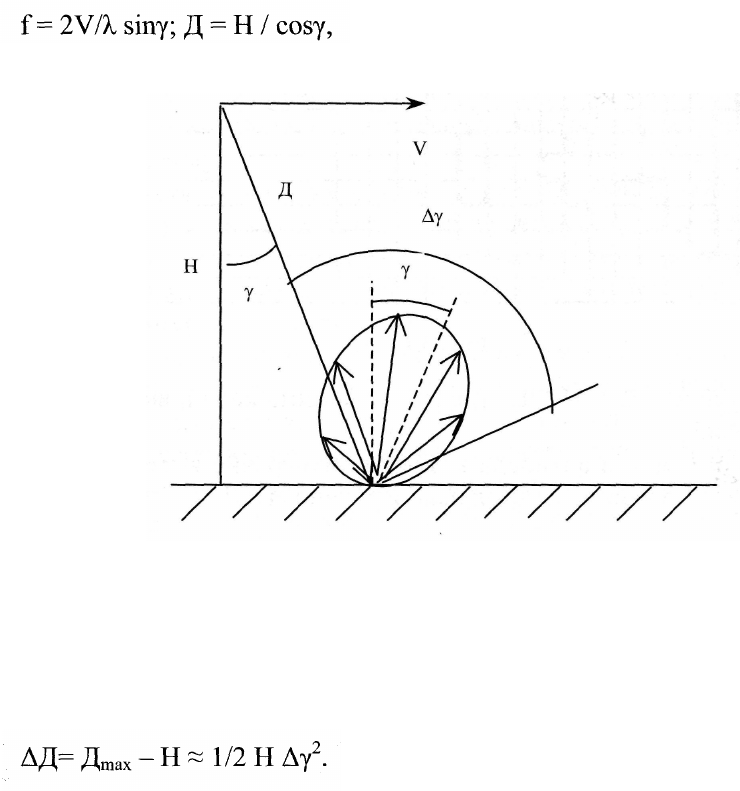
(3.1)

где V - скорость носителя РЛС.

Рис. 3.2

Если ширина индикатрисы рассеяния поверхности составляет Δγ, то мак-

симальное значение дальности Д

тах

= Η /cos(Ay) и протяженность этих сигна-

лов по дальности

При отражении электромагнитных волн от крупномасштабных пологих

неровностей ширина индикатрисы рассеяния Δγ по порядку величины равна

среднеквадратическому значению углов наклона поверхности. При работе над

пересеченной местностью ее средняя величина по косвенным оценкам состав-

ляет порядка 30°, что соответствует протяженности альтиметровых отражений

по дальности до одного километра и более.

Другой характерной особенностью является их азимутальная протяжен-

ность. Флуктуации интенсивности и, соответственно, распределение отметок в

координатах дальность-частота, обусловлены неодинаковым затенением даль-

них лепестков диаграммы направленности элементами конструкции самолета

при вращении антенны. Особенно этот эффект заметен при эволюциях самоле-

та по крену.

За счет сканирования по азимуту сигналы на последовательных кадрах

подвергаются амплитудной модуляции диаграммой направленности. Поэтому

конфигурация отметок от одной и той же цели на соседних кадрах может быть

различной, даже без учета собственных флуктуации отраженного сигнала.

Наиболее изменчива конфигурация альтиметровых отметок.

При работе РЛС в режиме низкой частоты повторения зондирующих сиг-

налов отметки имеют более простую структуру. Каналы обнаружения дискре-

тизированы по дальности и азимуту. Число каналов дальности может состав-

лять несколько тысяч, и их дискретность соответствует темпу съема данных

после сжатия зондирующих импульсов. В РЛС S-диапазона за время радиоло-

кационного контакта с целью при сканировании антенны по азимуту излучает-

ся не более пяти-семи импульсов (в зависимости от периода повторения). Для

оптимального обнаружения такой пачки отраженных сигналов применяют не-

когерентное накопление импульсов в каждом канале дальности в скользящем

по азимуту окне (нерекурсивная фильтрация) или в рекурсивном фильтре не

выше второго порядка. Решение об обнаружении принимается на каждом пе-

риоде зондирования. В результате азимутальный дискрет отметок соответству-

ет периоду повторения зондирующих импульсов.

В РЛС Р-диапазона пачка может состоять из 32 и более импульсов зонди-

рования, что позволяет реализовать доплеровскую фильтрацию. При этом кад-

ры БПФ могут перекрываться во времени. В этом режиме отметка имеет номер

канала дальности и номер доплеровского канала, а азимутальный дискрет оп-

ределяется степенью перекрытия кадров обработки. Для получения приемле-

мой точности измерения азимута обычно достаточно пяти-семи отметок в пре-

делах пачки.

В режиме работы по воздушным целям, находящимся за дальностью ра-

диогоризонта, полностью отсутствуют отражения от подстилающей поверх-

ности. При работе по надводным объектам возможно обнаружение целепо-

добных сигналов («долбяков»), отраженных от взволнованной морской по-

верхности.

В РЛС Р-диапазона обычно присутствуют непреднамеренные помехи от

различных наземных узкополосных источников излучения, которые режекти-

руются по частоте.

Несинхронные импульсные помехи устраняются на этапе когерентной об-

работки путем сглаживания резких перепадов уровней сигнала. Такая обработ-

ка может применяться и в РЛС S-диапазона в режиме излучения с высокой час-

тотой повторения. Обнаруженные помеховые отметки могут селектироваться в

режиме СДЦ по их протяженности в частотной и временной областях.

3.1.2. Принципы алгоритмов формирования

первичных радиолокационных измерений

Основной задачей алгоритмов формирования первичных радиолокацион-

ных измерений является получение «на проходе» оценок координат обнару-

женных отметок. Измерение координат осуществляется в несколько этапов в

соответствии с пространственно-временной структурой отраженных сигналов.

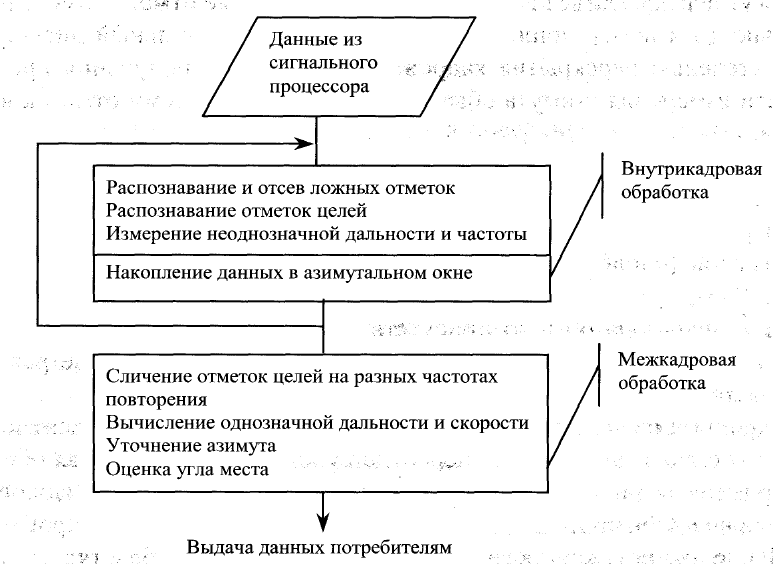
В режиме излучения с высокой частотой повторения сначала проводится

внутрикадровая обработка информации, полученной на кадре с одной часто-

той повторения, затем - межкадровая обработка информации, объединяющая

данные с последовательных кадров в пределах некоторого азимутального окна.

Основные задачи внутрикадровой обработки:

распознавание и отсев помеховых отметок;

распознавание образов целей в координатах задержка-частота;

измерение неоднозначной дальности и частоты полученных групп отметок.

На этапе межкадровой обработки основной задачей являются идентифи-

кация и совместная обработка отметок от одной и той же цели, полученных на

различных частотах повторения. В результате совместной обработки вычисля-

ются однозначная дальность, однозначная радиальная скорость, уточняется

азимут цели. В режиме измерения высоты путем сканирования либо моноим-

пульсным методом оценивается угол места цели.

Структурная схема алгоритмов измерений приведена на рис. 3.3.

Рис. 3.3

Обработка в режиме низкой частоты повторения также разделяется на

этапы, если при обработке сигналов проводится доплеровская фильтрация. В

этом случае внутрикадровая обработка по своим задачам и принципам реали-

зации не отличается от обработки в режиме с высокой частотой повторения. В

задачи межкадровой обработки входят уточнение частоты и дальности и изме-

рение азимута по амплитудной информации обнаруженной пачки.

При обнаружении загоризонтных воздушных целей обычно измеряются

только дальность и азимут цели. Эти измерения проводятся по информации,

накопленной в течение азимутальной пачки.

На этапе внутрикадровой обработки в режиме работы с высокой частотой

повторения селекция помеховых отметок проводится по априорной информа-

ции об их характерных признаках, описанных выше. Жесткая связь между час-

тотой и дальностью альтиметровых отражений позволяет распознавать их и

режектировать. Кроме того, возможна селекция «альтиметра» по азимутальной

протяженности.

Необходимо отметить, что наиболее эффективна борьба с такими помеха-

ми на ранних этапах обработки. Так, возможно сформировать отдельный канал

когерентной обработки, работающий со слабонаправленной антенной, луч ко-

торой ориентирован вертикально вниз. Сигналы, обнаруженные в этом и в ос-

новном каналах, идентифицируются как альтиметровые. Также возможна на-

стройка алгоритма обнаружения с учетом нерэлеевского распределения ампли-

туд альтиметровых сигналов.

Задача распознавания образов решается в бортовом процессоре. Обычно

применяется упрощенный алгоритм группирования отметок в двумерной об-

ласти, основанный на критерии связности. Алгоритмы поиска положения мак-

симума (или «центра тяжести») полученной области реализуют работу двумер-

ного дискриминатора.

Простейшим способом решения задач группирования и измерения являет-

ся выбор на кадре единственной отметки с максимальной амплитудой. Более

сложным является способ, при котором границы группы определяются после-

довательно по каждой координате с вычислением средневзвешенного значения

этой координаты. Например, в элементе дальности формируется связная об-

ласть отметок по частоте и определяется среднее значение частоты по этой об-

ласти. Затем процедура повторяется для следующего элемента дальности, и ес-

ли дальности смежные, а их частоты достаточно близки, то отметки объединя-

ются в группу. Накопление проводится до тех пор, пока выполняются эти

условия. Затем замеры частоты усредняются по всей группе и определяется ве-

личина неоднозначной дальности.

Измерение частоты проводится на основе гипотезы наличия в одном эле-

менте дальности единственной цели или неразрешаемой по частоте группы це-

лей. При этом амплитудный профиль отметок должен соответствовать априор-

ной форме спектра цели и для измерения можно применить простые алгоритмы

одномерной интерполяции положения максимума или алгоритмы дискримина-

тора. Отклонение частоты сигнала от некоторого опорного значения вычисля-

ется путем весового суммирования амплитуд с антисимметричными коэффи-

циентами и амплитудной нормировки [12].

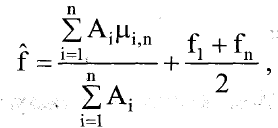
Оценка частоты сигнала f, выраженная в номерах гармоник дискретного

преобразования Фурье (ДПФ), вычисляется по формуле

(3.2)

где Ai - амплитуда отметки в группе, состоящей из η отметок; μ^ - весовые ко-

эффициенты, зависящие от числа η анализируемых отметок; f

- номера час-

тотных каналов соответственно первой и последней отметок из группы.

В зависимости от выбора коэффициентов по этой формуле определяется

положение или максимума, или медианы, или «центра тяжести» спектра. Прак-

тически одинаковые по точности результаты дают алгоритмы интерполяции

положения максимума и медианы.

Точность измерений при прочих равных условиях зависит от типа приме-

няемого окна в процедуре ДПФ. На рубежах обнаружения окно типа «косинус

квадрат» позволяет достигнуть величины ошибки порядка 1/5 ширины частот-

ного дискрета. Эта ошибка характеризует точность измерения сдвига частоты

сигнала относительно несущей. Если компенсатор доплеровской частоты, обу-

словленной собственной скоростью носителя отсутствует, то измеренная час-

тота соответствует радиальной скорости относительного движения цели и РЛС.

Если компенсация проводится, то измеренная частота соответствует радиаль-

ной скорости цели относительно земли. При этом фактический сдвиг частоты

компенсирует собственное движение с ошибкой из-за навигационных ошибок,

и ошибок системы подстройки частоты. Поэтому точность алгоритма измере-

ния доплеровской частоты определяет точность измерения относительной ра-

диальной скорости цели.

Повышение точности измерения частоты на этапе внутрикадровой обра-

ботки не является самоцелью, а предназначено для повышения достоверности

межкадровой обработки при устранении неоднозначности по дальности. В

процессе сличения отметок, обнаруженных на разных частотах повторения, ос-

новным критерием является инвариантность радиальной скорости. Поэтому

уменьшение ошибок измерения частоты уменьшает ошибки неправильного

сличения и вычисления неоднозначной дальности.

Обычно разрешение целей в пределах компактной области отметок не

проводится, так как для этого требуется высокое отношение сигнал/шум, а до-

зорные РЛС обычно вынуждены работать на максимальных дальностях, когда

отношение сигнал/шум минимально.

Для повышения точности измерения координаты дальности может приме-

няться интерполяция, если амплитудный профиль отметок по дальности извес-

тен (соответствует форме автокорреляционной функции сигнала). В противном

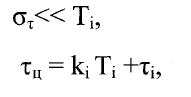
случае могут приниматься различные решения в зависимости от тактической

обстановки и текущей решаемой задачи радиотехнического комплекса. Напри-

мер, в группе может выделяться отметка с минимальной дальностью (головная

цель) или с максимальной амплитудой. При наличии достаточно точного целе-

указания от системы сопровождения выделяется отметка с указанной дально-

стью. При группировании отметок по дальности недопустимо определять сред-

невзвешенную дальность, как это делается при оценке частоты. Это объясняет-

ся тем, что малая ошибка измерения неоднозначной дальности (на 1-2

элемента) приводит к ошибке вычисления однозначной дальности в десятки и

сотни километров.

На этапе межкадровой обработки основной задачей является объединение

результатов внутрикадровой обработки, полученных на соседних кадрах, вы-

числение однозначной дальности и скорости и уточнение азимута цели. Прин-

ципиальное различие между этапами обработки заключается в следующем.

Если при внутрикадровом группировании обычно известен ожидаемый

образ цели в координатах группирования (функция неопределенности сигнала

на одной частоте повторения), то при межкадровом группировании это не име-

ет места. Неизвестны неоднозначная дальность и частота на другой частоте по-

вторения, сигнал искажен флуктуациями и модулирован по амплитуде азиму-

тальной ДН антенны. Кроме того, наличие на одном кадре отметок от несколь-

ких целей или ложных отметок практически не ухудшает достоверность

внутрикадровой информации. В то же время функция неопределенности сигна-

ла на соседних кадрах в этих условиях становится многопиковой и создает не-

однозначность при группировании отметок. Ошибки межкадрового группиро-

вания приводят к значительным ошибкам вычисления однозначной дальности,

что эквивалентно пропуску на трассе истинной отметки и обнаружению лож-

ной отметки на ошибочно вычисленной дальности.

Методы устранения неоднозначности по дальности (УНД) до одиночной

(разрешаемой по другим координатам) цели различаются алгоритмами реше-

ния задачи восстановления числа по его остаткам, к которой сводится эта зада-

ча при детерминистском подходе.

Обозначим через т

истинную (однозначную) задержку сигнала цели, че-

рез Tj - неоднозначную задержку, полученную при работе с периодом повторе-

ния Tj. Тогда для восстановления значения т

, пренебрегая ошибками измере-

ния имеем систему уравнений

(3.3)

где kj - неизвестные целые числа.

Для удобства анализа выберем новую единицу измерения задержки Δ та-

кую, что все периоды повторения, выраженные в этом масштабе, являются вза-

имно простыми числами. Для этого достаточно выразить значения Tj в виде ра-

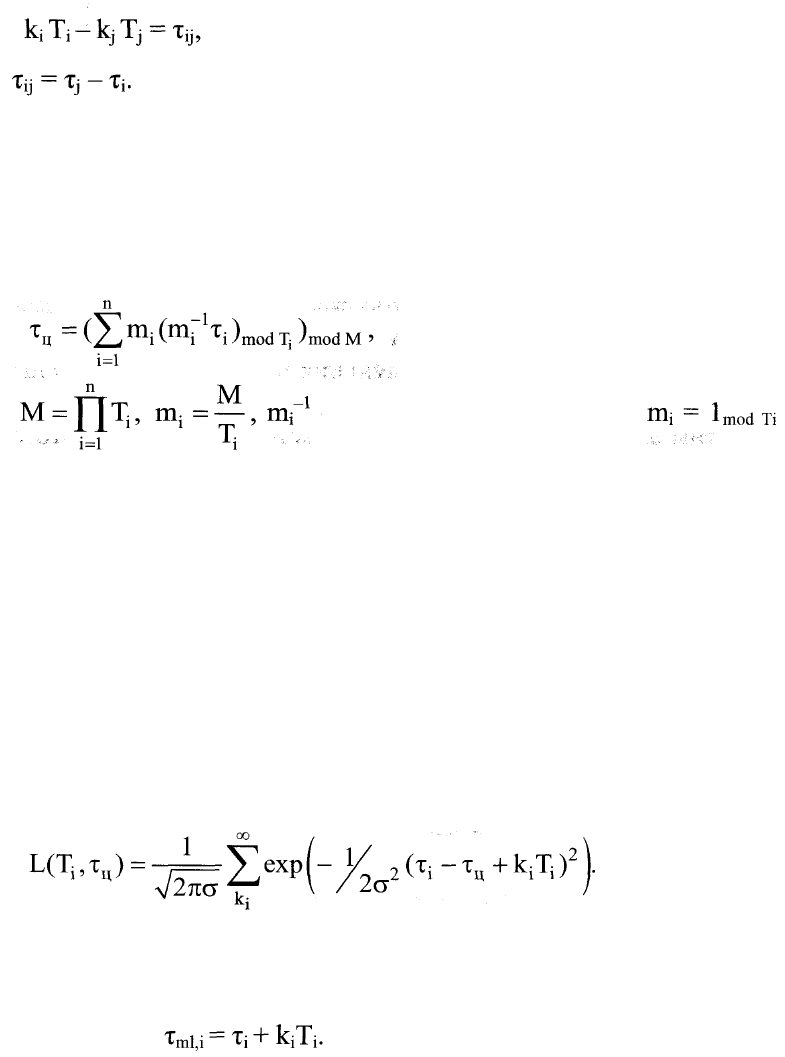
циональных дробей, и тогда величина Δ будет равна отношению наибольшего

общего делителя числителей к наименьшему общему кратному знаменателей.

Вычитая попарно уравнения системы (3.3), получаем диофантовы уравнения в

целых числах вида

(3.4)

где

Для существования решения необходимо, чтобы величина ц была кратна

наибольшему общему делителю чисел Tj,Tj. Поскольку они являются взаимно

простыми, то величина ц должна быть округлена до целого числа.

Способ решения таких уравнений был известен Диофанту и Евклиду. По-

сле введения Гауссом понятий вычетов и сравнения по модулю решение запи-

сывается в замкнутом виде:

(3.5)

где - решение уравнения mf

(константы,

которые могут быть вычислены заранее).

Нахождение решения системы уравнений (3.4) может быть сведено к по-

иску по таблице, при котором не требуются логические операции и арифмети-

ческие вычисления.

Более строгое решение задачи как статистической оценки неизвестного

параметра основывается на теории многошкальных измерений. Будем для про-

стоты полагать ошибки измерения неоднозначных задержек гауссовыми со

среднеквадратическим значением σ

, одинаковым для каждого из периодов по-

вторения T

и независимыми для различных периодов повторения. Тогда для

функции правдоподобия L однозначной задержки т

, полученной по результату

измерения τ\, имеем следующее выражение:

(3.6)

Фактический диапазон изменения чисел ki определяется допустимым ин-

тервалом значений ошибки измерения истинной задержки т

. Максимально

правдоподобная оценка задержки т

у по результатам этого измерения является

неоднозначной:

Можно показать, что при объединении независимых измерений на η пе-

риодах повторения максимально правдоподобная оценка задержки τ достигает-

ся при таких значениях k

которые минимизируют дисперсию неоднозначных

замеров Тщц, усредненную по всем η измерениям:

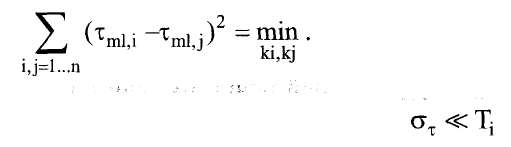
При малой ошибке измерения значения к

{

, максимизирующие

функцию правдоподобия, единственны и, очевидно, совпадают с решением

системы уравнений (3.4). Тогда оценка однозначной задержки т

получается

как среднее арифметическое оценок т

у при к

{

= kj.

Таким образом, задача УНД сводится к выявлению тем или иным образом

дальности, на которой происходит максимальное число совпадений неодно-

значных оценок дальностей. Поиск такой однозначной дальности может быть

проведен различными способами: прямым перебором вариантов, табличным

способом, путем решения системы уравнений в целых числах по формуле (3.5)

и другими.

Описанные выше методы измерения дальности основаны на разделении

решения этой задачи на два этапа. Первый этап состоит в нахождении точеч-

ных оценок неоднозначных задержек на каждой из используемых частот по-

вторения, второй этап - в нахождении искомой однозначной дальности по по-

лученным на первом этапе оценкам с учетом априорной информации. Как было

показано выше, каждый из этапов может выполняться с различной степенью

строгости в статистическом описании моделей наблюдаемых и оцениваемых

параметров. Однако, как правило, ограничиваются нормальными законами

распределения, что является адекватным лишь при достаточно больших отно-

шениях сигнал/шум (более 20...25 дБ) и не позволяет учесть (в статистическом

смысле) наличие слепых зон приема, обусловленных запиранием приемника на

время излучения и наличия коррелированных помех от подстилающей поверх-

ности. Кроме того, на первом этапе для нахождения точечных оценок неодно-

значных задержек обычно используют обнаружение сигнала, что сопряжено с

появлением ошибок 1-й 2-го родов. Число и значения используемых частот

повторения являются фиксированными и обычно не зависят от дальности и те-

кущего отношения сигнал/шум, что приводит к низкой вероятности правильно-

го измерения дальности при слабых сигналах и неоправданному затягиванию

процедуры разрешения неоднозначности при сильных сигналах.

Развитие вычислительной техники позволило решить задачу раскрытия

неоднозначности по дальности в БРЛС в общем виде. При этом проводится:

определение оптимальных значений частот повторения, обеспечивающих

максимальный прирост информации в процессе их перебора;

определение необходимого числа частот повторения для обеспечения за-

данной вероятности правильного измерения;

статистическая оптимизация алгоритмов определения неоднозначной за-

держки по дальности;

оптимизация процедуры раскрытия неоднозначности;

оптимизация учета априорных данных о координатах цели и ее парамет-

рах движения (целеуказание по дальности и скорости) [17].

На каждой ЧПИ перед излучением следующей пачки импульсов с другой

ЧПИ проводится определение оптимального значения частоты повторения,

обеспечивающей максимальный прирост информации о дальности до цели.

Тем самым обеспечивается адаптация алгоритма измерения к текущей дально-

сти до цели (выбираются преимущественно «прозрачные» частоты) и к теку-

щему отношению сигнал/шум.

На каждой частоте повторения по имеющимся комплексным амплитудам

принятого сигнала в стробах дальности на выходе спектроанализатора вычис-

ляется функция правдоподобия неоднозначной задержки в пределах периода

повторения с учетом «слепых» зон и уровня мешающих отражений (помех) в

зоне приема. Важно заметить, что при этом нет необходимости в пороговой об-

работке, и соответственно, отсутствуют потери. В свою очередь отсутствие по-

роговой обработки позволяет увеличить число ЧПИ при сохранении общего

измерения, что повышает вероятность правильного измерения дальности.

Оценка дальности проводится по критерию максимума апостериорной

плотности вероятности, для вычисления которой используются априорная

плотность вероятности и информация об изменении дальности до цели в про-

цессе измерения.

Применение указанного метода позволяет получить выигрыш до шести

децибел.

Существенные трудности возникают при обнаружении нескольких нераз-

решаемых по частоте и азимуту целей (тактической группы). В этой ситуации

задача УНД не сводится к известной задаче оценки параметров сигнала при

наличии мешающих сигналов. В нашем случае сигналы являются ортогональ-

ными и обнаруживаются независимо друг от друга. Проблема измерения связа-

на не с деформацией главного максимума выходного эффекта (проблема ло-

кальной точности), а с неоднозначностью измерений (проблема глобальной

точности). Такая задача относится к разряду некорректно поставленных: во-

первых, ее решение не единственно, во-вторых, оно неустойчиво. Регуляриза-

ция возможна только при наличии априорной информации, достаточной для

выработки единственного решения.

При отсутствии такой информации вероятности ошибочных решений рас-

считываются при упрощающих предположениях:

для однозначного измерения дальности во всем требуемом диапазоне дос-

таточно двух различных частот повторения;

периоды повторения, выраженные в подходящем временном масштабе, -

взаимно простые числа;

неоднозначные дальности целей случайны и равномерно распределены в

пределах каждого периода повторения;