Валишев М.Г., Повзнер А.А. Лекции по колебаниям и волнам

Подождите немного. Документ загружается.

вектор



излучаемой диполем ЭМВ, располагается в плоскости, проходящей

через ось диполя. Причем вектор



направлен по касательной к меридиану, а

вектор



располагается в плоскости, перпендикулярной к оси диполя, по

касательной к параллели.

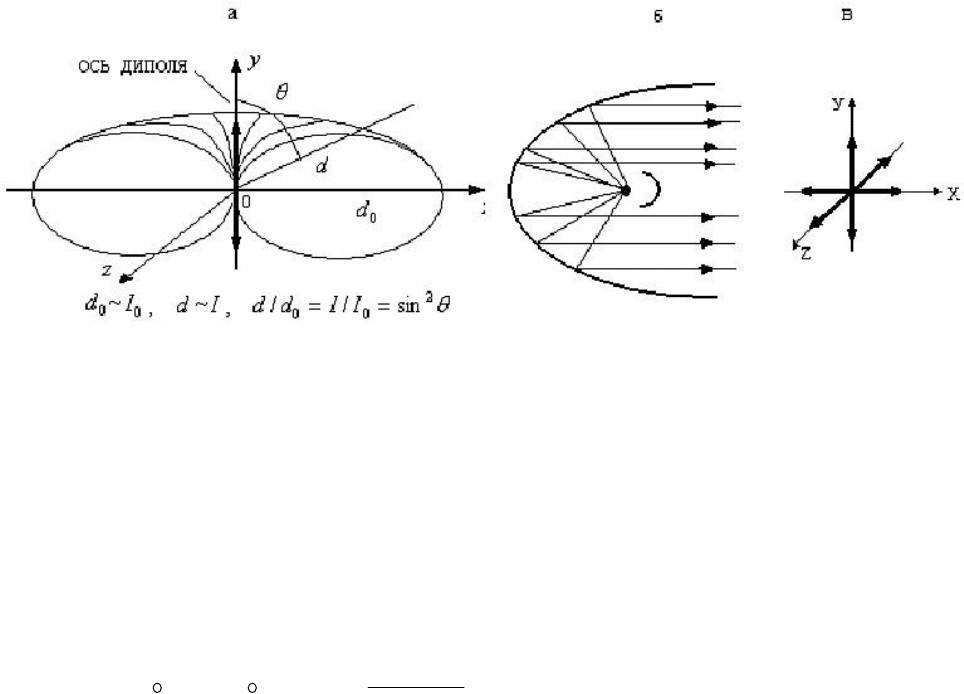
2. Диаграмма направленности излучения диполя. Эта диаграмма показывает

распределение энергии излучения по всем направлениям в пространстве. На

ней откладываются отрезки прямой, длина которых пропорциональна

интенсивности ЭМВ, излучаемой в данном направлении. Для диполя

〉

〈

sin θ ,

sin θII=

, (6.64)

где

I – максимальная интенсивность излучаемых электромагнитных волн.

Из формулы (6.64) можно сделать следующие заключения: 1) диаграмма

направленности излучения обладает осевой симметрией, так как

интенсивность

не зависит от угла

(рис. 6.20,в); 2) максимальная

интенсивность излучения наблюдается по всем направлениям, лежащим в

плоскости, перпендикулярной к оси диполя (

θ90, sin90

==); 3) вдоль

оси диполь не излучает ЭМВ (

θ0, sin0 0II

). Диаграмма направленности

излучения диполя является достаточно широкой и, образно говоря,

представляет собой бублик "без дырки".

Рис. 6.20

Применяя разные комбинации различных излучателей ЭМВ можно получить

различные диаграммы направленности излучения. Так, например, узкую

диаграмму направленности излучения - параллельный пучок ЭМВ можно

получить, если поместить источник излучения в фокусе параболического

зеркала (рис. 6.20,б), а самую широкую диаграмму направленности излучения -

сферическую, дают три взаимно перпендикулярных диполя (рис. 6.20,в).

3.Мощность излучения ЭМВ. Открытый колебательный контур. В

соответствии с формулой (6.63), мощность и интенсивность излучения диполя

можно выразить следующим образом:

SdSP



∫

dSE

22 2

sin

πθ

∫

rdd

aq ~

ωq

ωp .

ωp , (6.65,а)

〉〈=

aq ~

ωq

ωp . (6.65,б)

Итак, мощность и интенсивность излучаемой диполем электромагнитной

волны прямо пропорциональны четвертой степени частоты колебаний его

зарядов. Следовательно, увеличение частоты колебаний зарядов диполя

приводит к резкому увеличению мощности излучаемых им ЭМВ. Поэтому

выгодно передавать сигналы на большие расстояния с помощью ЭМВ высокой

частоты.

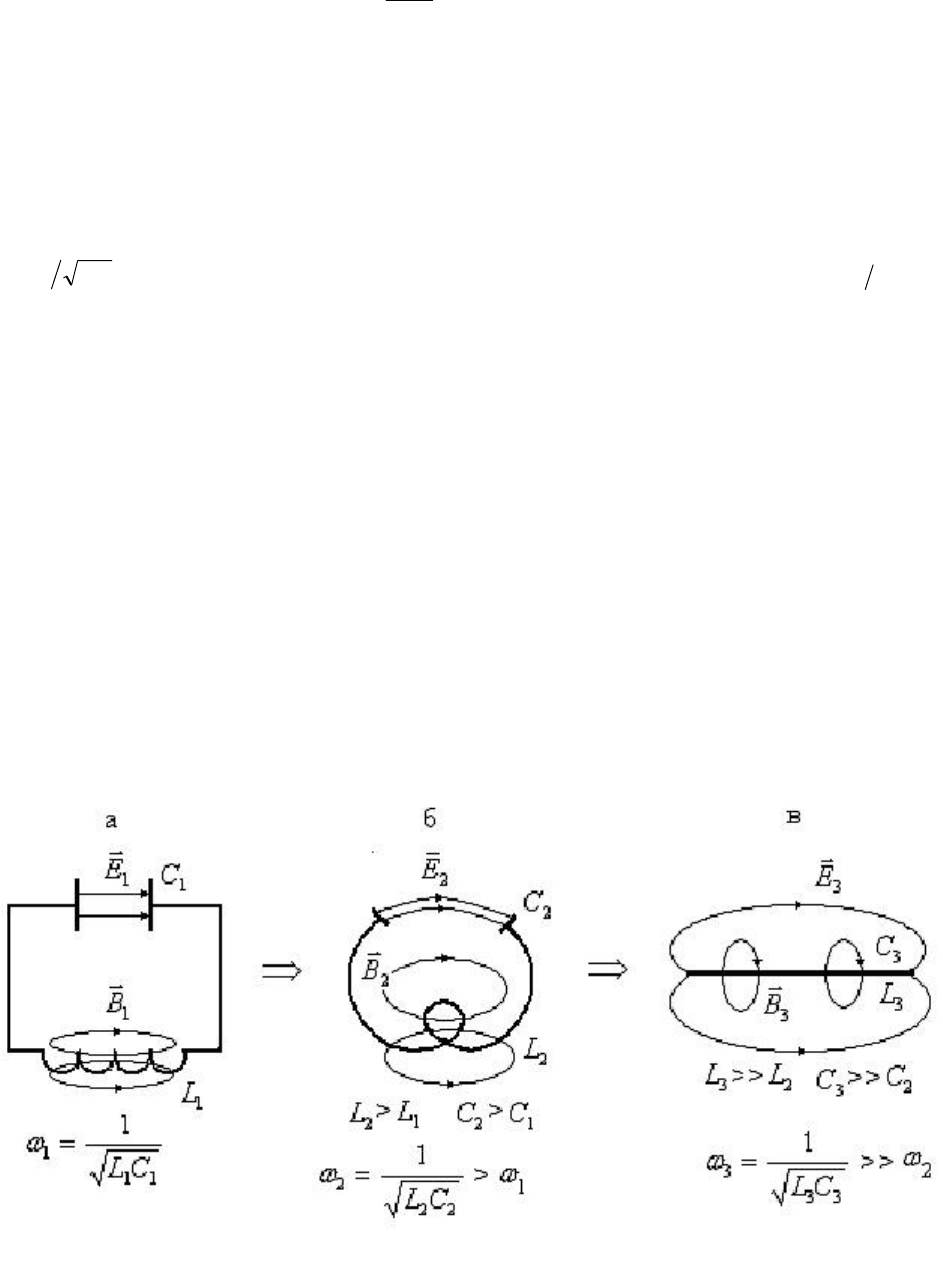
Для повышения циклической частоты собственных колебаний контура

(

LC1=ω

) необходимо уменьшать емкость С конденсатора ( dSС

εε= , т.е.

уменьшать площадь его пластин и увеличивать расстояние между ними) и

уменьшать индуктивность катушки (

VnL

µµ=

, т.е. уменьшать число ее

витков). Это в итоге приводит к открытому колебательному контуру

(рис. 6.21,в).

Он представляет собой отрезок проводника (антенну), в котором

возбуждаются высокочастотные электромагнитные колебания. Они излучаются

в пространство в виде ЭМВ большой мощности. Открытый колебательный

контур также называют полуволновым диполем, так как на его длине

укладывается половина длины волны, излучаемой антенной, или вибратором

Герца. Отметим, что в антенне перекрываются электрическое и магнитное поля,

это существенно повышает мощность излучения ЭМВ по сравнению с

закрытым колебательным контуром.

В связи с резким повышением мощности излучения высокочастотных

колебаний передача сигнала звуковой частоты на большие расстояния

происходит за счет модуляции

ВЧ колебаний сигналом звуковой частоты. При

Рис. 6.21

приеме модулированного ВЧ сигнала проводят его детектирование, т.е.

отделяют звуковой сигнал от высокочастотного колебания.

Впервые ЭМВ экспериментально были обнаружены Герцем (1888 г.) с

помощью открытого колебательного контура. Возбуждая в нем затухающие ВЧ

колебания, он с помощью такого же приемного колебательного контура

принимал ЭМВ и тем самым доказал факт их существования и подтвердил

теорию Максвелла.

6.2.5. Опыты с ЭМВ

В этом параграфе приводятся некоторые опыты, подтверждающие свойства

ЭМВ.

1. Электромагнитные колебания в излучаемом полуволновом диполе

(изучение стоячей ЭМВ волны в диполе).

Генератор УВЧ создает в

индуктивно связанной с ним антенне гармонические колебания частоты ν=150

МГц или длины волны λ =2 м.

Антенна представляет собой отрезок проводника длиной



=λ/2=1 м., что

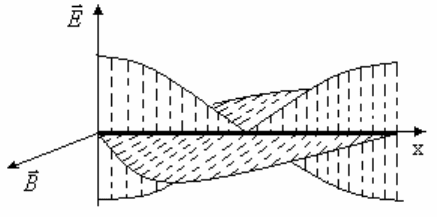
соответствует полуволновому диполю. В ней устанавливаются стоячие волны:

1) стоячая волна электрического поля – на краях проводника наблюдаются

пучности, а посередине – узел этой стоячей волны; 2) стоячая волна магнитного

поля – для нее на краях проводника образуются узлы, а посередине – пучность

стоячей волны (рис. 6.22).

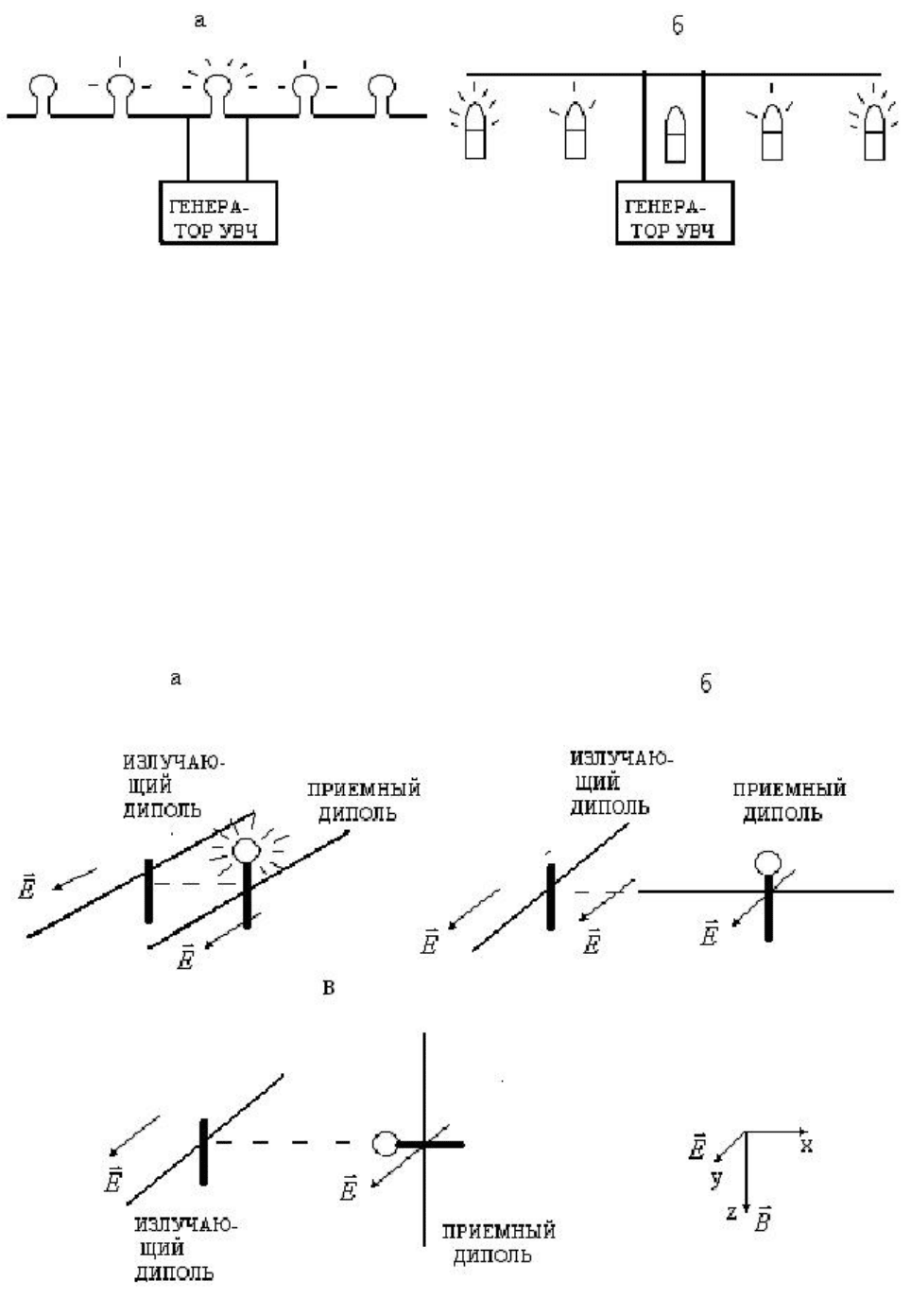
Это можно наглядно показать, если

взять

проводник, в который вставлены

лампочки на разных расстояниях от его

середины. Лампочка в середине

проводника имеет наибольшую яркость,

так как здесь располагается пучность

стоячей волны магнитного поля. Яркость

лампочек спадает при переходе к краям

проводника, где находятся узлы стоячей Рис. 6.22 ываваываы

волны магнитного поля (рис. 6.23,а). Напомним, что модуль вектора

магнитной

индукции пропорционален силе тока в проводнике.

Если взять газоразрядную лампочку, которая светится под

действием

электрического поля, то тогда ее свечение будет наиболее ярким на краях

проводника, где находятся пучности стоячей волны электрического поля, и

свечение будет отсутствовать в середине проводника (рис. 6.23,б). Отметим,

что он (см. рис. 6.22) обладает осевой симметрией, т.е. его можно поворачивать

вокруг оси Ох на произвольный угол.

Рис. 6.23

2.Расположение векторов



в излучаемой диполем ЭМВ. Покажем, что

вектор



в излучаемой диполем ЭМВ совершает колебания в плоскости,

проходящей через ось диполя, а вектор



– в плоскости, перпендикулярной

оси диполя. Отметим, что в данном случае диполь излучает цилиндрическую

волну.

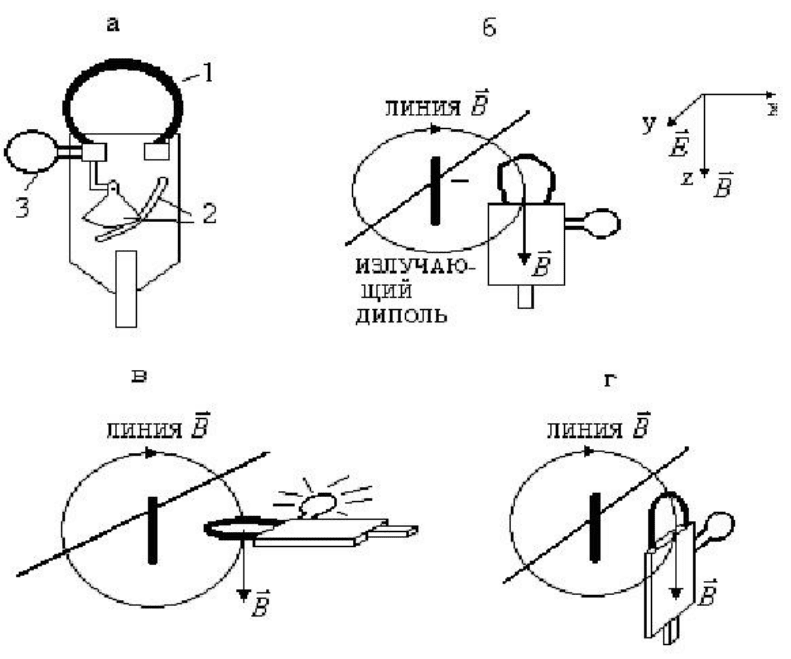
Расположим параллельно передающему диполю составной диполь такой же

длины, две равные части которого замкнуты лампочкой накаливания

(рис.6.24,а). При этом лампочка ярко светится, так как вектор



излучаемой

ЭМВ располагается вдоль оси приемного диполя (рис. 6.24,в) и поэтому

возбуждает в нем интенсивное движение электронов, и возникающий при этом

электрический ток достаточен для яркого свечения лампочки. Кроме того,

Рис. 6.24

равенство длины приемного и излучаемого диполей (отрезков прямолинейного

проводника) приводит к явлению резонанса, что резко усиливает вынужденные

колебания в приемном диполе.

По мере поворота приемного диполя яркость свечения лампочки

уменьшается и, когда диполи оказывается перпендикулярными друг к другу,

лампочка гаснет: вектор



, перпендикулярный к длине диполя, не может

возбудить в нем интенсивных движений электронов (рис. 6.24,б, в).

Рассмотрим теперь расположение вектора



в излучаемой диполем ЭМВ. Для

этого используем резонирующий контур. Он состоит из последовательно

соединенных между собой проволочного витка 1, конденсатора переменной

емкости 2 (за счет изменения площади перекрытия пластин конденсатора) и

лампочки накаливания 3 (рис. 6.25,а).

Вначале располагают контур вблизи генератора и путем изменения емкости

конденсатора добиваются максимальной яркости свечения лампочки. Затем

контур

помещают на некотором расстоянии от передающего диполя

поочередно в положениях б, в и г (рис. 6.25,б, в, г). Лампочка светится лишь

тогда, когда диполь оказывается в плоскости витка (рис. 6.25,в). При этом

колебания вектора



приводят к неравному нулю магнитному потоку через

плоскость контура, изменение которого со временем приводит к

возникновению ЭДС индукции в витке. В случаях же (б) и (г) вектор



колеблется в направлении, параллельном плоскости витка (линии



не

пересекают плоскости витка), и магнитный поток будет равен нулю и ЭДС

индукции в контуре не возникает.

Рис. 6.25

Таким образом, этот опыт показывает, что вектора



взаимно

перпендикулярны, вектор



лежит в плоскости, проходящей через ось диполя,

а вектор



– в плоскости, перпендикулярной к оси диполя.

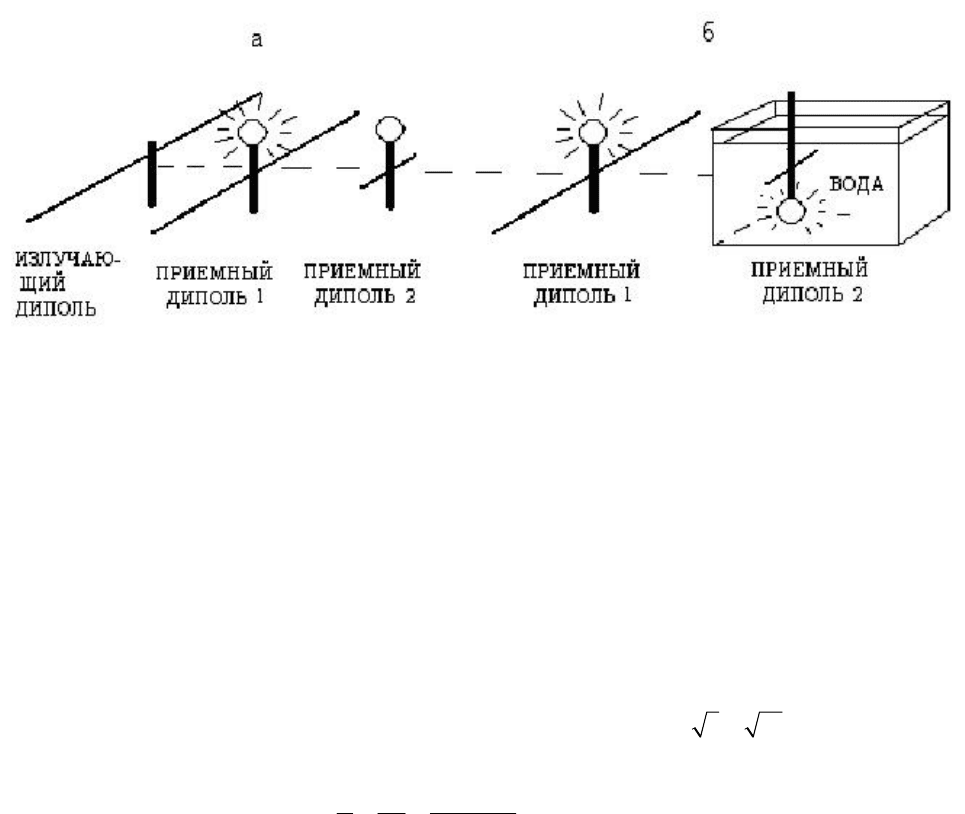
3. Влияние среды на скорость распространения ЭМВ. На равных

расстояниях от излучающей антенны (диполя) длиной



=1 м, параллельно ей,

располагают два приемных диполя с лампочками посередине. Один из них

имеет длину



=1 м, а другой, короткий,



=0,1 м. При включении генератора

лампочка в длинном приемном диполе загорается, а в коротком – нет

(рис.6.26,а).

Это объясняется явлением резонанса. В приемной антенне возникают

вынужденные колебания под действием приходящей к ним ЭМВ. При

совпадении частоты колебаний приходящей на приемную антенну ЭМВ с

собственной частотой колебаний приемной антенны как открытого

Рис. 6.26

колебательного контура амплитуда вынужденных колебаний в ней резко

возрастает. Для приемного диполя такой же длины, как и излучающий диполь,

наступает явление резонанса (лампочка загорается), чего нельзя сказать о

коротком приемном диполе – для него явление резонанса отсутствует, и

лампочка в нем не загорается.

Затем, не меняя расположения диполей, помещают короткий

диполь в сосуд

с водой (рис. 6.26,б). В этом случае загораются лампочки в обоих диполях. Тот

факт, что в коротком диполе загорается лампочка, связано с влиянием среды на

скорость распространения ЭМВ. Действительно, для ЭМВ СВЧ – диапазона

абсолютный показатель преломления для воды равен

ε819

==n , и поэтому

длина волны в воде будет равна

310

0,1

91,510

⋅

== = ≈

⋅⋅

νν

и для короткого диполя длины



=0,1 м (λ=0,1 м) в воде наблюдается также

явление резонанса, и лапочка, включенная в него, светится.

6.2.6. Ударные волны. Уединенные волны

Помимо традиционно изучаемых типов волн можно привести примеры и

других видов волн, которые занимают особое место при анализе процессов

распространения колебаний в различных средах.

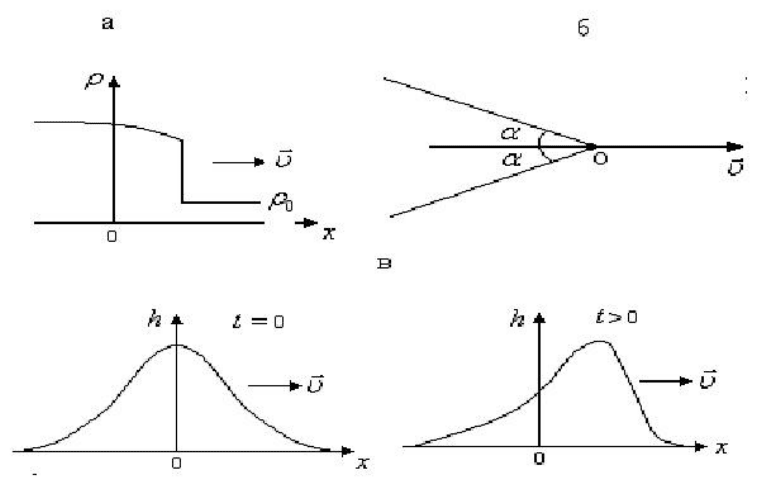
1. Ударная волна. Ударная волна (скачок уплотнения) - это

распространяющаяся со сверхзвуковой скоростью тонкая переходная область, в

которой происходит резкое увеличение плотности, давления и скорости

вещества. Она возникает при взрывах, детонации, при сверхзвуковых

движениях тел, при мощных электрических разрядах и т.д. Например, при

взрыве образуются продукты взрыва, обладающие большой плотностью и

находящиеся под

большим давлением. Расширяющиеся продукты взрыва

сжимают окружающий воздух, причем в каждый момент времени сжатым

оказывается лишь воздух, находящийся в определенном объеме, вне этого

объема воздух остается в невозмущенном состоянии. С течением времени

объем сжатого воздуха возрастает. Поверхность, которая отделяет сжатый

воздух от невозмущенного воздуха, и представляет собой ударную волну (или

как

говорят, фронт ударной волны). На рис. 6.27,а в качестве примера приведен

график распределения плотности в ударной волне, распространяющейся в

реальном газе (

ρ – плотность газа перед фронтом волны).

При ускоренном движении тела ударная волна возникает не сразу.

Сначала возникает волна сжатия с непрерывными распределениями плотности

и давления. С течением времени крутизна передней части волны возрастает и в

некоторый момент времени происходит резкий скачок всех гидродинамических

величин, возникает ударная волна.

В случае движения тела

со сверхзвуковой скоростью ( υυ>

ВУКА

) звуковые

волны охватывают лишь часть объема газа, лежащую позади движущегося тела

и ограниченную некоторой поверхностью, называемой характеристической

поверхностью, поверхностью слабого разрыва или фронтом ударной волны.

Рис. 6.27

При сверхзвуковом движении тела малых размеров со скоростью υ

характеристическая поверхность (фронт волны) имеет вид круговой конической

поверхности, вершина которой совпадает с движущемся телом О, а угол

между образующими и траекторией тела удовлетворяет условию:

sin υ/υ=

ЗВУКА

. Этот угол называют углом слабых возмущений или углом Маха

(рис. 6.27,б).

В случае электромагнитных волн аналогом ударной звуковой волны,

возникающей при движении тел со скоростями, превышающими фазовые

скорости упругих волн в данной среде, является излучение Вавилова –

Черенкова (см. §7.4.4).

2. Уединенная волна представляет собой волновое движение, которое в

каждый момент времени локализовано в конечной области пространства и

относительно медленно изменяет свою структуру при распространении.

Типичная, уединенная волна имеет вид одиночного импульса или перепада, но

она может иметь и более сложную структуру. К уединенным волнам относят

такие типы нелинейных волн, как уединенные волны в диссипативных средах,

стационарные импульсные волны возбуждения в активных средах (нервные

импульсы) и солитон в среде без потерь.

Солитон (от лат. solus – один

) – структурно устойчивая уединенная волна в

нелинейной диспергирующей среде. Структура солитона поддерживается

стационарной за счет баланса между действием нелинейности среды и

дисперсии.

Солитон впервые наблюдался на водяном канале в 1834 г., когда при резкой

остановке баржи около ее носа образовался водяной выступ (водяной холм) и

затем он стал самостоятельно распространяться по каналу

, сохраняя на

протяжении длительного времени свою структуру и скорость.

Рассмотрим возможность образования солитона на поверхности воды. Для

волн, у которых длина

л волны значительно превышает глубину

водоема

(

λ >> H

, мелкая вода) явление дисперсии отсутствует, они распространяются с

фазовой скоростью

υ()=+gH h

, где

– ускорение свободного падения, а

смещение поверхности жидкости в вертикальном направлении в данной точке

профиля волны (см. рис. 6.27,в). Из записанной формулы для фазовой скорости

следует, что вершина водяного холма движется быстрее, чем точки вблизи его

подножия. Это

нелинейность среды приводит к тому, что крутизна фронта

волны возрастает с течением времени, т.е. происходит пространственное

сужение водяного холма (см. рис. 6.28,б).

Если же длина

волны будет значительно меньше глубины

водоема

(

H<<

), то в этом случае для волн малой амплитуды наблюдается сильная

дисперсия

, т.е. их фазовая скорость зависит от длины волны /(2π)g=

υλ

. Это

приводит к расплыванию водяного холма. Оказывается, что существуют волны

с таким соотношением между

л и максимальным возвышением

max

h , при

котором наблюдается компенсация процессов расплывания холма из-за явления

дисперсии и процессов его пространственного сужения. Такая компенсация и

соответствует существованию солитона.

Солитоны ведут себя подобно частицам: при взаимодействии между собой

или с некоторыми другими возмущениями, солитоны не разрушаются, а

расходятся, вновь сохраняя свою структуру неизменной.

Солитоны играют важную роль в теории конденсированного состояния

вещества, в частности в квантовой статистике

, теории фазовых переходов.

Структуры в форме солитонов обнаружены во многих динамических системах

– в плазме, радиосхемах, лазерах, нервных волокнах.

Учебное издание

Марс Гильманович Валишев

Александр Александрович Повзнер

ФИЗИКА

Часть 4

КОЛЕБАНИЯ И ВОЛНЫ

Редактор О.С. Смирнова

Корректор М.Ю. Петров

Подписано в печать 19.03.2006 Формат 60× 84 1/16

Бумага типографская Офсетная печать Усл.печ.л. 5,05

Уч.-изд. л. 5,8 Тираж 1000 Заказ Цена "С"

Редакционно-издательский отдел ГОУ ВПО УГТУ – УПИ

Ризография НИЧ ГОУ ВПО УГТУ – УПИ

620002, Екатеринбург, Мира, 19