Валишев М.Г., Повзнер А.А. Лекции по колебаниям и волнам
Подождите немного. Документ загружается.

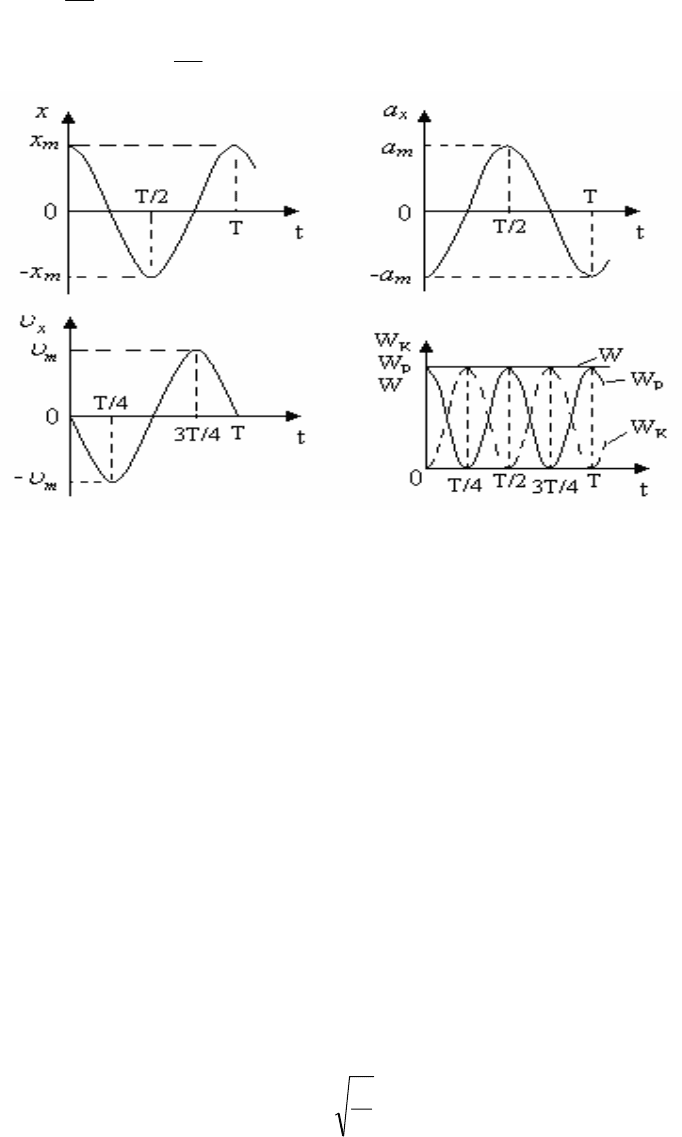
11
(рис. 5.4, начальная фаза колебаний считается равной нулю: 0
0
=ϕ ). При
построении графиков удобно записать уравнения колебаний в виде
)
2
cos()cos(
0
t
T
xtхх
mm
π
=ω=
и выбирать моменты времени, равные
0, / 4, / 2, 3 / 4,t ТТ ТТ= ⇒
1;0;1;0;1)
2
cos( −=
π
t
T
.
Рис. 5.4
Отметим, что для потенциальной и кинетической энергий период
гармонических колебаний оказывается в два раза меньше, чем для смещения х.
5.5. Квазиупругая сила. Математический и физический маятники.
Гармонический осциллятор
Докажем следующее утверждение: если в системе результирующая
сила является квазиупругой, то в такой системе происходят
гармонические колебания. Под квазиупругой силой
Rу
F
понимают силу,
которая подчиняется закону Гука, но не является по своей природе
упругой силой.
Докажем это утверждение. Учтем, что, для F
Ку
выполняется
одновременно и второй закон Ньютона и закон Гука, из которых можно
получить дифференциальное уравнение колебаний в системе
()
RУ XX
Fmakx
=
=− , ⇒
m
k
=ω
0
,
0
2
0
=ω+
′′
х
,
где
k – коэффициент жесткости системы, х- смещение тела (м.т.) от
положения равновесия.
Как уже было отмечено выше, решением такого дифференциального
уравнения является гармоническое колебание (5.7), что и требовалось доказать.
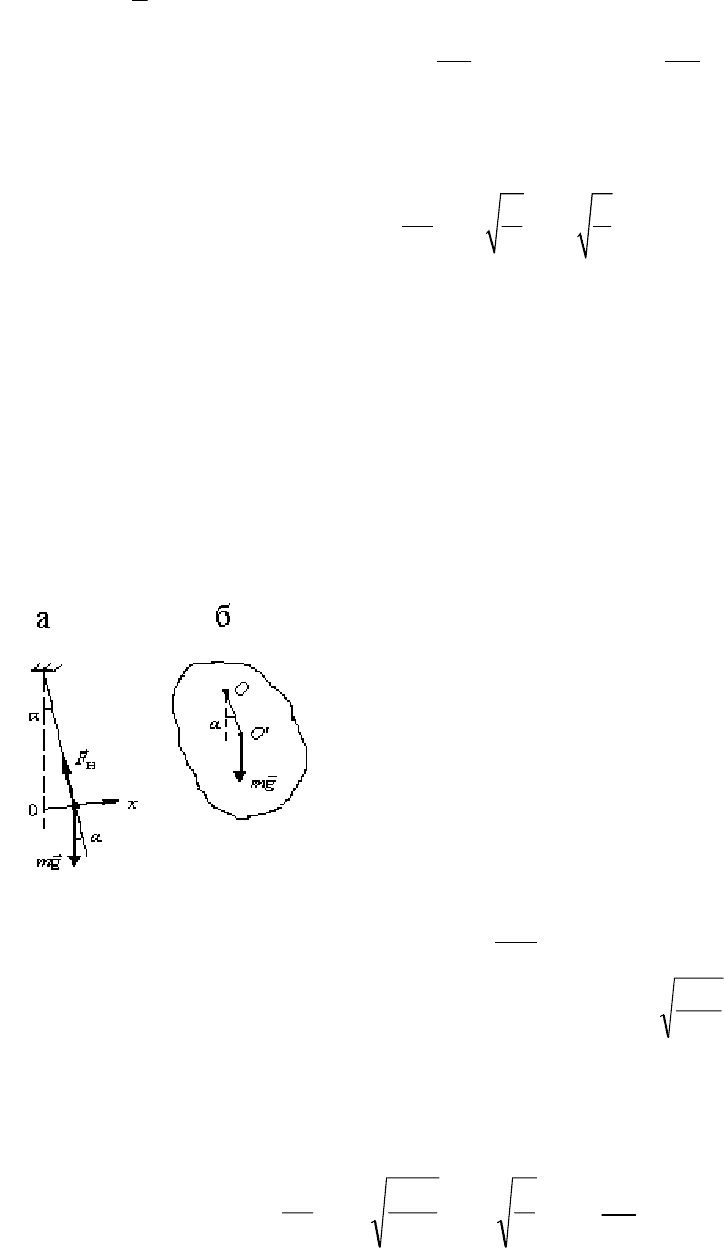
12
В качестве примера справедливости этого утверждения рассмотрим
колебания математического маятника - это материальная точка массы m,
подвешенная на невесомой нерастяжимой нити длины l (рис. 5.5,а)
Найдем проекцию на ось Ох результирующей силы, действующей на груз
математического маятника. Учитывая малые значения угла отклонения
α
(
sin tg
x
l
αα
≈≈
) запишем
⇒−=−=−=+ kxx
l
mg
mggmF
XH
α
sin)(
l
mg
k =
.
Итак, при малых отклонениях от положения равновесия (при малых
амплитудах колебаний) колебания груза будут гармоническими. Это позволяет
найти период колебаний
0
2
22
ω
== =
ml
T
kg
π
ππ
. (5.14)
Как следует из формулы (5.14), период колебаний математического
маятника будет зависеть от длины нити l и числового значения ускорения g
свободного падения.
Рассмотрим теперь общий случай - случай колебаний физического
маятника.
Физическим маятником называют твердое тело, способное под
действием силы тяжести совершать колебания вокруг неподвижной
горизонтальной оси (точка О, рис. 5.5,б).
При этом ось вращения не проходит
через центр тяжести (центр масс) тела (точка О', рис. 5.5,б). Расстояние между
точками О и О' обозначено буквой а (ОО' =а).
Покажем, что при малых углах отклонения
α
(
α
≈
α
sin
) от положения равновесия (ему
соответствует расположение точек О и О' на
одной вертикальной прямой) колебания
физического маятника будут гармоническими.
Для этого запишем второй закон Ньютона для
вращательного движения в векторном виде и в
проекциях на ось вращения (см. раздел
"Механика", формула (1.46))
MI
=
ε
, α−=
α
sin
2
2
mga
dt
d
I ,
α−=α
′′
mgaI
,
0
2
0
=αω+α
′′
⇒
)cos(
00
ϕ+ωα=α t
m
,
I
mga
=ω
0
. (5.15)
Как уже было отмечено выше, решением полученного
дифференциального уравнения является гармоническое колебание. Тогда для
периода колебаний физического маятника можно записать следующую
формулу:
g
l
mga
I
T
n
π=π=
ω
π
= 22
2
0
,
n
I
l
ma
=
. (5.16)
Рис. 5.5
13
где введена приведенная длина физического маятника
n
l - это такая
длина математического маятника, при которой периоды колебаний физического
и математического маятников совпадают.
Рассмотренные выше примеры (колебательный контур, математический и
физический маятники, колебания груза на пружине) являются частными
случаями движения гармонического осциллятора. Под осциллятором (от
латинского слова oscillo-качаюсь) понимают любую физическую систему,
совершающую колебания. Если колебания в системе
будут гармоническими, то
такой осциллятор называют гармоническим осциллятором. Для
механических систем результирующая сила в этом случае является
квазиупругой, а потенциальное поле, в котором движется тело, имеет
параболический вид (
2/)(
2
kxxU = ), что наблюдается при малых отклонениях х
системы от положения равновесия.
Если отклонение
x
нельзя считать малым, то тогда в разложении
)(xU
по
степеням
x
необходимо учитывать члены более высокого порядка
(потенциальное поле становится не параболическим:
...2/)(
32
++= xkxxU
α
),
уравнения движения становятся нелинейными, а сам осциллятор в этом случае
называют ангармоническим осциллятором.
Понятие осциллятора применяется также и к немеханическим
колебательным системам. В частности, колебательный контур является
электрическим осциллятором.
5.6. Гармонические электромагнитные колебания в закрытом
идеальном колебательном контуре
В такой контур не подается внешнее напряжение (U
ВНЕШ
=0) и в нем
отсутствуют потери энергии на нагревание проводников (β=0), поэтому общее
дифференциальное уравнение колебаний (5.1) для такого контура запишется
таким образом:
0
2
0
=ω+
′′
qq
, (5.17)
решением этого уравнения является гармоническое колебание
ϕ
=
ϕ
+
ω
= cos)cos(
00 mm
qtqq . (5.18)
Используя таблицу аналогий между механическими и
электромагнитными колебаниями (табл. 5.1), можно переписать формулы (5.9) -
(5.13) для случая колебательного контура. Таким способом можно получить
зависимости от времени силы тока I, напряжения на конденсаторе U
C
,
напряжения на катушке U
L
, ЭДС самоиндукции
S
ε
, энергий электрического
поля конденсатора W
C
и магнитного поля катушки W
L
, полной энергии
колебаний W и проекций вектора напряженности
X
E
электрического поля
конденсатора и вектора магнитной индукции
X
B
магнитного поля катушки.
Итак, эти формулы имеют следующий вид:

14
ϕ−=
′
= cos
m
IqI
,
mm
qI
0
ω= ,
ϕ== cos
CmC
U
C
q
U
,
C
q
U
m
Cm
=
, (5.19)
ϕ−=
′′
= sin
LmL
UqLU ,
Cm
m
mLm
U
C
q
qLU ==ω=
2
0
,
LS
UqL
−
=
′
′
−
=
ε
, (5.20)
ϕ
2
2
sin
2
MmM
W
LI
W ==
,
2
2
m
Mm
LI
W =
,
ϕ
2
ЭЛm
2
ЭЛ
cos
2
W
C
q
W =
,
C
q
W
m
2
2
ЭЛm
=
, (5.21)
22
22
ЭЛmЭЛ
mm
MmM
LI
C
q
WWWWW ====+=
, (5.22)
ϕ== cos
m
C
X
E
d
U
E
,
d
U
E
Cm
m
=
,
ϕ
−
=
sin
mX
BB ,
V
L
IB
mm
0
µ
=
, (5.23)
где d– расстояние между обкладками плоского конденсатора; V – объем
катушки (она представляет собой длинный соленоид);
0
µ
– магнитная
постоянная.
5.7. Сложение гармонических колебаний
5.7.1. Векторная диаграмма. Сложение гармонических
колебаний одного направления и одинаковой частоты
Возьмем ось
Ox
. Из начала оси (точка О) отложим вектор
А
под углом
0
ϕ
к
оси
Ox
(рис. 5.6). Если этот вектор вращать вокруг точки
O
с угловой
скоростью
ω
, то тогда проекция вектора
А
на ось
Ox
будет изменяться по
гармоническому закону
0
cos)0( ϕ= Ax , )cos()(
0
ϕ
+
ω
=
tAtx .
Такое построение называют векторной диаграммой. Гармоническое
колебание на векторной диаграмме совершает проекция вектора
А
на ось
Ox
.
Причем циклическая частота
ω
колебаний будет равна по модулю угловой
скорости
ω
вращения вектора
А
.
Пусть тело (м.т.) одновременно участвует в двух гармонических колебаниях
одинаковой частоты, происходящих в одном
направлении, причем амплитуды и начальные
фазы колебаний различны (
21
AA ≠
,
0201
ϕ
ϕ
≠ ):
)cos(
0111
ϕ
+
ω
=
tAx , )cos(
0222
ϕ+ω
=
tAx . (5.24)
Результирующее движение, равное сумме
колебаний
1
x
и
2
x
, будет также
гармоническим колебанием той же
циклической частоты
ω
Рис. 5.6

15
)cos(
021
ϕ
+
ω
=
+
= tAxxx .
Необходимо найти амплитуду и начальную фазу результирующего колебания.
Это можно сделать с помощью векторной диаграммы. Для этого проведем из
точки О векторы с амплитудами А
1
и А
2
под углами
01
ϕ
и
02
ϕ к оси
Ox
и
приведем их во вращение с угловой скоростью
ω
(рис. 5.7).
Проекции векторов
1
А
и
2
А
на ось
Ox
при этом совершают гармонические
колебания в соответствии с уравнениями (5.24). Результирующее колебание
будет изображаться проекцией на ось
Ox
вектора
А
, полученного из векторов
1
А
и
2
А
по правилу параллелограмма. Из построения на Рис. 5.7 следует, что
квадрат амплитуды вектора
А
можно найти по теореме косинусов из
треугольника ∆ОА
2
А:
γ−+= cos2
21
2
2
2
1
2
AAAAA
, ϕ∆−π=ϕ
−
ϕ
−
π
=
γ
)(
0102
ϕ∆++= cos2
21
2
2
2
1
2
AAAAA
. (5.25)
Из треугольников ∆ОА
1
В и ∆ОАС для начальной фазы
0
ϕ
результирующего
колебания можно найти следующее выражение:
101202
0
101202
sin sin
tg
cos cos
+
==
+
AA
AC
OC A A
ϕ
ϕ
ϕ
ϕ
ϕ
. (5.26)
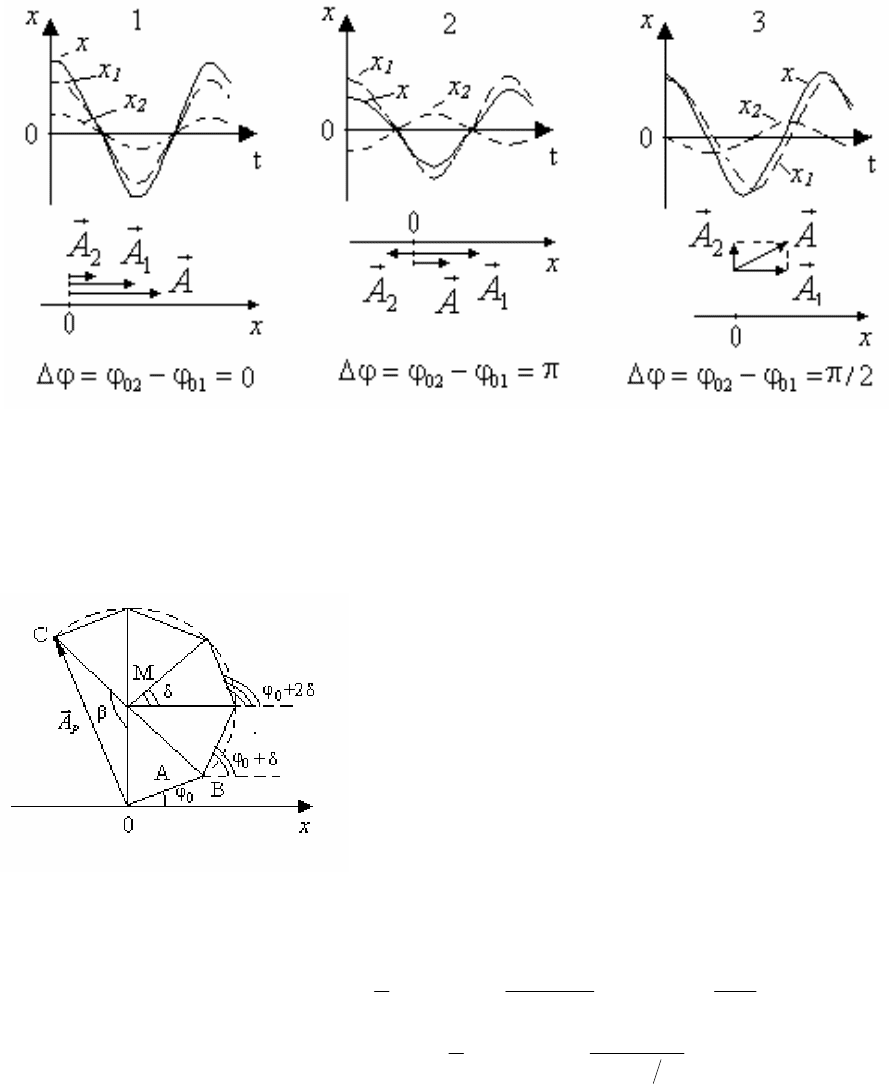
Рассмотрим частные случаи сложения колебаний.
1.
02 01
2 , 0,1,2,...nn
ϕ
ϕϕ π
∆= − = =
21
AAA
+
=
⇒
, (5.27)
т.е. если разность фаз складываемых колебаний равна четному числу π, то
колебания максимально усиливают друг друга.
2.
()
02 01
2 1 , 0,1,2,...nn
ϕϕ ϕ π
∆= − = + =
21
ААA −=⇒ , (5.28)
т.е., если разность фаз
складываемых колебаний
равна нечетному числу π, то
колебания максимально
ослабляют друг друга.
3.
2
π
=ϕ∆
2
2
2
1
ААA +=⇒
.
На рис. 5.8 приведены результаты
сложения гармонических
колебаний в рассмотренных выше
случаях 1,2 и 3, при условии, что
01
ϕ =0 и А
1
>
А
2
.
Рис. 5.7
Полученные условия максимального усиления (5.27) и ослабления (5.28)
колебаний при сложении колебаний одного направления и одинаковой частоты
будут использованы при изучении интерференции когерентных волн.
16
5.7.2. Сложение N гармонических колебаний одного направления,
одинаковой амплитуды и частоты, начальные фазы которых образуют
арифметическую прогрессию
Рассмотрим сложение N гармонических колебаний, происходящих вдоль
оcи
Ox
)cos(
01
ϕ
+ω= tAx
,
)cos(
02
δ
+
ϕ
+
ω
= tAx
,
)2cos(
03
δ
+
ϕ
+
ω
=
tAx
,…,
(
)
()
N0
xAcost N1=ω+ϕ+−δ
.
Рис. 5.8
Найдем с помощью векторной диаграммы амплитуду А
Р
результирующего
колебания (рис. 5.9). Для этого отложим вектор первого колебания амплитуды
А из точки О, он будет составлять угол φ
0
с осью Ох; вектор второго колебания
будем откладывать из конца первого вектора,
угол между вторым вектором и осью Ох будет
равен (φ
0
+δ) и т.д. В результате получается
ломаная линия, вписанная в окружность
радиуса R. Вектор результирующего
колебания замыкает эту ломаную линию и
определяется следующим образом
β2πδ δ
: 2 sin 2 sin( ) 2 sin
22 2
−
∆== =
Р
NN
ОМС А ОМ OM OM
δ
:2sin
22sin(δ2)
∆==⇒=
A
OMB OB A R OM
,
что позволяет написать
Рис. 5.9
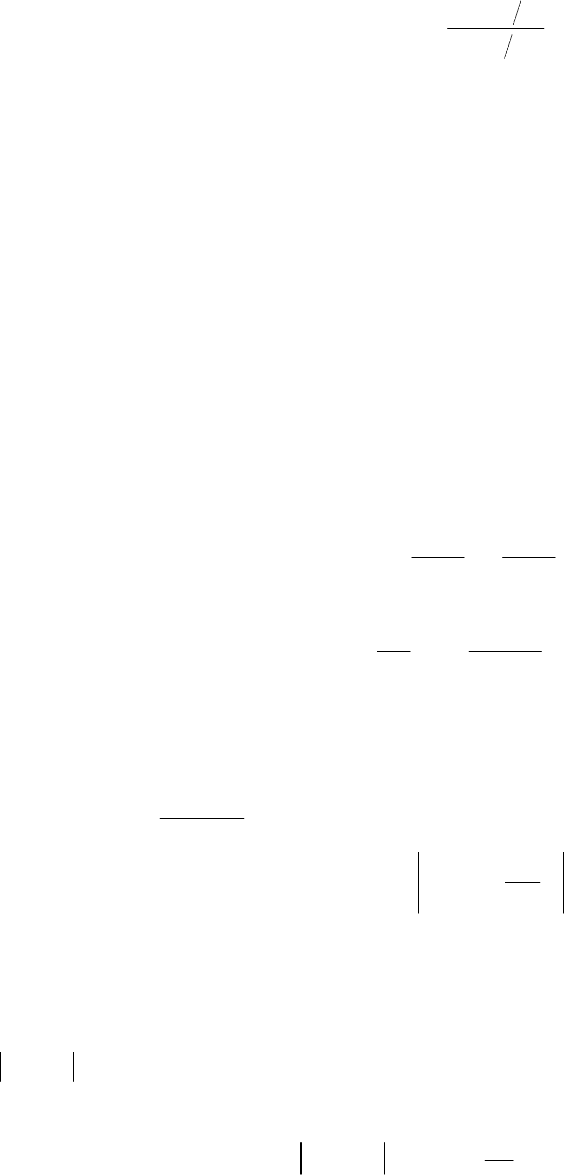
17
sin( δ2)
sin(δ2)
=
P
N
AA
. (5.29)
Полученная формула будет использована при расчете результата многолучевой
интерференции на дифракционной решетке.
5.7.3.
Биения
Биения – это колебания, которые получаются в результате сложения
двух гармонических колебаний х
1
и х
2
одного направления с близкими
частотами (
12
,ωω
>>
12
ω−ω=ω
∆
)/
21
xxx +
=
,
11 1
cos ω
=
x
At
,
22 2
cos ω
=
x
At
.
Рассмотрим подробнее результат сложения таких колебаний. Для простоты
расчетов будем считать, что амплитуды складываемых колебаний
одинаковы:
AAA ==
21
. Тогда используя известную формулу сложения
косинусов
2
cos
2
cos2coscos
β
+
α
β
−
α
=β+α
,
запишем
12
12
ωω
ω
2cos cos
22
+
∆
=+=
x
xx A t t. (5.30)
Первый сомножитель в выражении (5.30) изменяется со временем
значительно медленнее второго (
12
,
ωωω
<<∆ ) и поэтому можно считать, что
результирующее колебание
x
представляет собой колебание с циклической
частотой
()
12
ω+ω
ω=
2
и с изменяющейся со временем амплитудой
tAtA
Б
2
cos2)(
ω∆
=
. (5.31)
Итак, биения можно представить как колебания с периодически
изменяющейся амплитудой. Эти колебания не являются гармоническими
колебаниями.
В общем случае амплитуда биений изменяется в пределах, заключенных от
21
AA −
до (
21
AA +
). При этом период изменения амплитуды (период биений
Б
Т
)
и циклическая частота
Ω
биений будут определяться по формулам
12
ωωΩ= −
,
2π
=
Ω
Б
Т
. (5.32)
На рис. 5.10 приведены графики зависимости амплитуды биений
Б
A
и
смещения
x
м.т. от времени t.
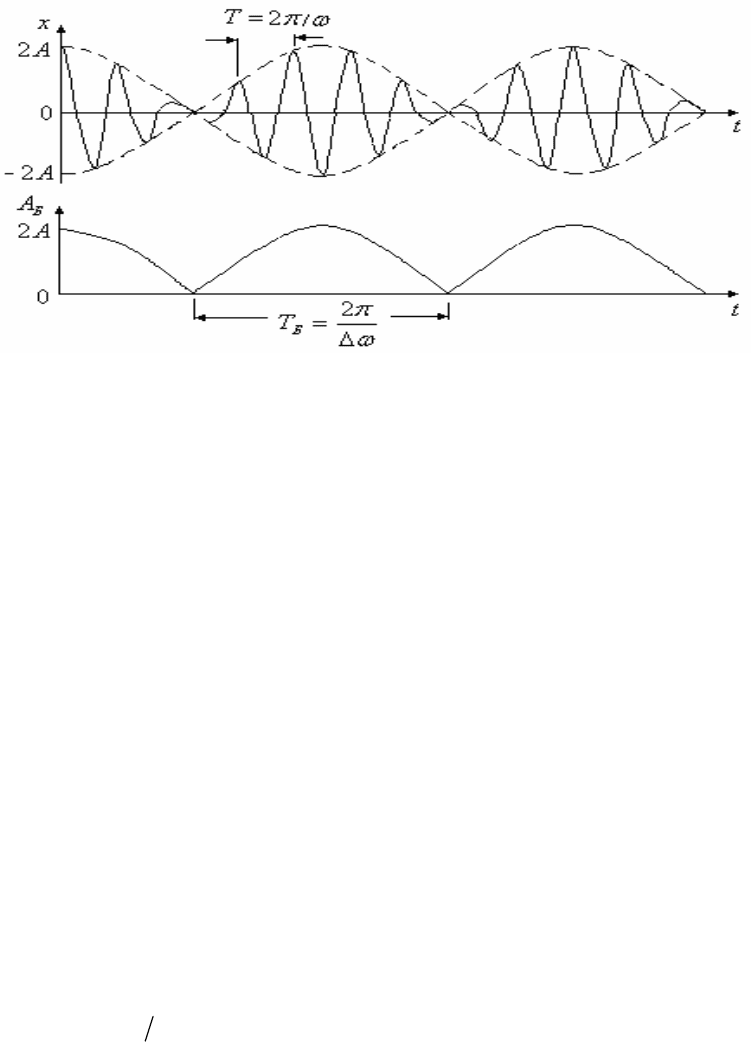
18
Рис. 5.10
Метод биений применяют, например, для настройки музыкальных
инструментов, при анализе восприятия звуков человеком.
Наглядно биения можно продемонстрировать на опыте, в котором
звуковой генератор возбуждает два колебания разной частоты, которые
человеческое ухо различает как два отдельных звуковых сигнала. Если
сближать частоты этих сигналов, то при некоторой разности частот (она
зависит от слухового восприятия конкретного человека) вместо двух сигналов
ухо человека будет воспринимать звуковой сигнал одной частоты, амплитуда
которого будет изменяться, т.е. в этом случае наблюдаются биения. При
дальнейшем сближении частот период биений будет увеличиваться и при
совпадении частот сигналов будет слышен звук одной частоты, амплитуда
которого не будет изменяться
.
Биения можно использовать, например, для определения частоты какого-
либо гармонического электрического колебания. Для этого на вход
осциллографа подают гармонические колебания от звукового генератора
(частоту
Г
ν
этих колебаний можно изменять) и гармонические колебания с
неизвестной частотой
ν
от какого-либо источника. По наблюдаемой на экране
осциллографа картине биений определяют период биений
Б
Т и частоту
колебаний (
1
Г
Б
Т
ν
ν
=± ). Знак плюс или минус в записанной формуле
определяется следующим образом: если при увеличении частоты
Г
ν
генератора
период биений, наблюдаемых на экране, увеличивается, то тогда в формуле
выбирается знак плюс (
Г
ν
ν
< ), в противном случае – знак минус (
Г
ν
ν
> ).
5.7.4. Сложение взаимно перпендикулярных колебаний.
Фигуры Лиссажу
Пусть тело (м.т.) одновременно участвует в двух взаимно перпендикулярных
колебаниях, происходящих вдоль осей
Ox
и
Oу
:
tАх
11
cos
ω
=
,
)cos(
22
ϕ
∆
+
ω
=
tAy
. (5.33)
19
В общем случае в результате сложения этих колебаний материальная точка
будет двигаться по траектории, определяемой соотношением их частот (
21
,
ω
ω
),
амплитуд (
21
, AA ) и разности начальных фаз
ϕ
∆
. Эти траектории можно описать
уравнениями, которые не содержат явно время t и определяют зависимость
координаты у от х. Форма этих траекторий и уравнения, описывающие их, и
представляют интерес при таком сложении колебаний.
Рассмотрим некоторые примеры сложения взаимно перпендикулярных
колебаний.
Пример 1.
,
21
ω
=
ω=ω . π=ϕ∆ ,0
Делим одно уравнение (5.33) на другое и получим
x
A
A
y
1
2
=
,
т.е. траектория результирующего движения представляет собой прямую линию,
лежащую в первой и третьей четвертях (рис. 5.11,а).
Если разность фаз
ϕ∆
складываемых колебаний равна π, то тогда прямая
линия будет располагаться во второй и четвертой четвертях (рис. 5.11,б). Угол
α на рис. 5.11– это угол наклона прямой к оси
Ox
, он определяется отношением
амплитуд складываемых колебаний (
0
=
∆
ϕ
:
2
1
tg
A
A
α
=
,
π
∆
=
ϕ
:
2
1
tg
A
A
α
=−
).
Рис. 5.11
Получаемое при этом движение м.т. является гармоническим колебанием,
так как изменение координаты r , определяющей положение м.т. на траектории
движения, происходит по гармоническому закону
tAAyxr ω+=+= cos
2
2
2
1
22
.
Такое движение м.т. также называют линейно поляризованным
колебанием. Оно повторяется через время, равное периоду складываемых
колебаний
ω
π
=
2
T
.

20
Пример 2.
2
3
,
2
,
21
π
π
=ϕ∆ω=ω=ω
:
)
2
для"(",sin,cos
21
π
=ϕ∆−ω=ω= t
A
y
t
A
x
∓
,
1
2
1
2
2
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
A
x
A
y
,
т.е. траектория результирующего движения является эллипсом, оси которого
совпадают с осями
Ox
и
Oу
(рис. 5.11,в).
В этом случае результирующее движение м.т., движущейся по эллипсу,
называют эллиптически поляризованным колебанием (для одинаковых
амплитуд колебаний
2
1
AA =
траектория движения становится окружностью, и
движение м.т. называют колебаниями, поляризованными по кругу). Такие
движения повторяются через время, равное периоду складываемых
гармонических колебаний (
ω
π
=
2
T
).
Рассмотрим направление движения м.т. по эллиптической траектории. В
момент времени t=0 м.т. находится в точке с координатами х=А, у=0. Для
разности фаз
2
π
=ϕ∆ ее движение по эллиптической траектории будет
происходить по направлению движения часовой стрелки, и соответственно
против движения часовой стрелки для разности фаз, равной
2
3
π
=ϕ∆
.
Действительно, если
2
π
=ϕ∆
, то тогда для малых значений времени t
координата у будет меньше нуля (
0sin
<
−
=
tу
ω
), что соответствует движению
по направлению часовой стрелки.
Если взять произвольное значение
ϕ
∆
( π,π2,π,3π2
∆
≠
ϕ
), то тогда
траектория результирующего движения будет также эллипсом, но ориентация
его осей будет зависеть от амплитуды складываемых колебаний и разности
фаз
ϕ∆
(рис .5.11,г).
Приведенные на рис. 5.11 траектории движения м.т. называют фигурами
Лиссажу. Они, в общем случае, получаются при сложении двух взаимно
перпендикулярных гармонических колебаний, отношение циклических частот
которых является кратным отношению целых чисел
(
1
ωω= n
,
2
ωω= m ,
2
1
ωω=
n
m
;
mn,
– целые числа). Тогда за промежуток
времени, равный наименьшему кратному периодов двух складываемых
колебаний
1
2π
ω
=T
n
и
1
2π
ω
=T
m
, движущаяся материальная точка возвращается
в начальное положение - получается замкнутая линия, она называется фигурой
Лиссажу.
Если в рассмотренных примерах 1 и 2 угловые частоты складываемых
колебаний незначительно отличаются друг от друга (
21 12
ωω ω,ωω,ω
=
+∆ ∆ ),
то такое различие в частотах можно трактовать как медленное изменение во
времени разности фаз складываемых колебаний
ϕ
∆
+
ω
∆
=
ω
−
ϕ
∆
+
ω=ϕ∆ tttt
12
))(()(
.
