Валишев М.Г., Повзнер А.А. Лекции по колебаниям и волнам
Подождите немного. Документ загружается.

21
Это приводит к тому, что вид фигуры Лиссажу будет непрерывно изменяться,
принимая вид траекторий движения, изображенных на Рис. 5.11. Поэтому,
наблюдаемое во времени изменение фигуры Лиссажу означает, что частоты
складываемых колебаний неодинаковы.
Пример 3.
12
ω=ω ,
0=
ϕ
∆
:
)12()1cos2(2cos
2
1
21
2
212
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=−ω=ω=
A
x
AtAtAy
,
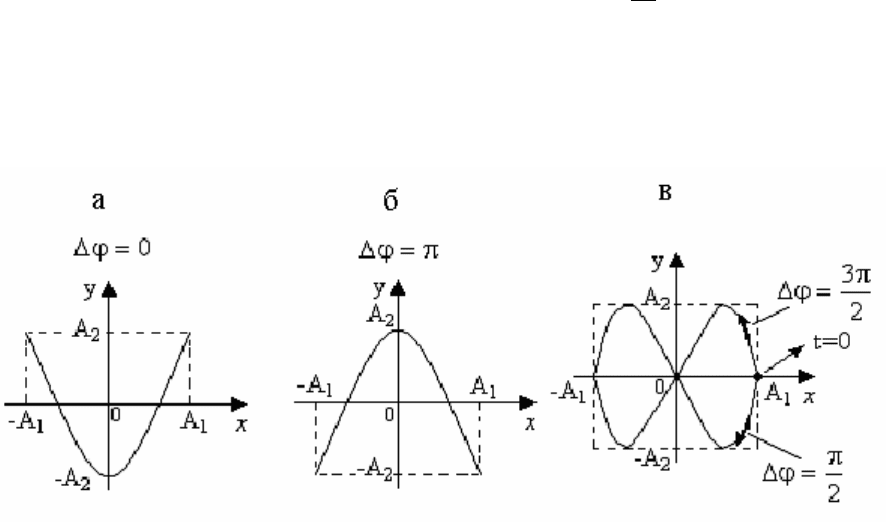
что дает фигуру Лиссажу в виде параболы (рис. 5.12,б). При других значениях
разности фаз получаются фигуры Лиссажу, вид которых приведен на рис. 5.12,б
и рис. 5.12,в.
Рис. 5.12
Отметим, что фигуры Лиссажу можно применять для определения частоты
какого-либо гармонического колебания (сигнала). Для этого нужно на входы х
и у осциллографа подать два сигнала – два гармонических колебания с
известной (колебание поступает от генератора электромагнитных колебаний,
его можно плавно изменять) и неизвестной частотой. Изменяя частоту
генератора можно добиться
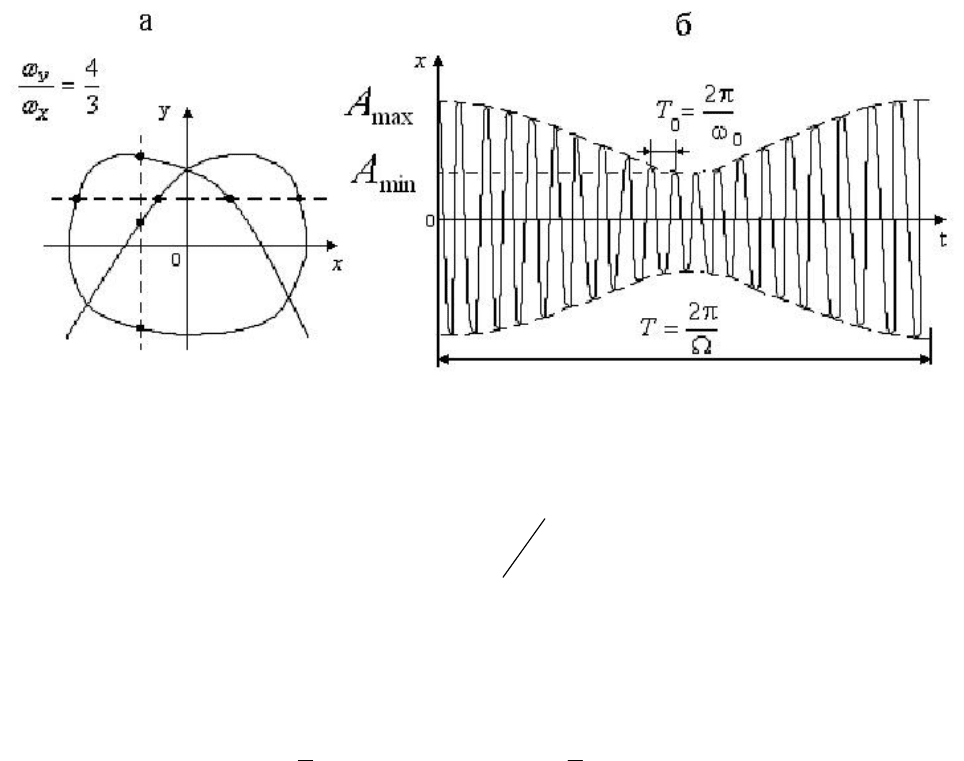
устойчивой фигуры Лиссажу и, зная по ее виду
отношение частот складываемых колебаний (отношение частот равно
отношению числа пересечений фигуры Лиссажу прямыми, параллельными
осям координат, рис. 5.13,а), определить неизвестную частоту.
5.7.5. Модулированные колебания
Под модуляцией колебаний понимают медленное (по сравнению с
периодом колебаний) изменение по определенному закону ее амплитуды,
частоты или фазы. Различают амплитудную, частотную или фазовую
модуляции.
В случае амплитудной модуляции амплитуду гармонического колебания
()
000
sin ω=+xA t
ϕ
можно изменять, например, по гармоническому закону -
)cos1()(
0
tmAtA Ω+= . Тогда модулированное колебание может быть записано в
следующем виде:
22
()
(
)
000
1cossinω=+ Ω +xA m t t
ϕ
, (5.34)
где частота изменения амплитуды
Ω
(ее называют частотой модуляции, она
описывает скорость изменения амплитуды колебания) должна быть во много
раз меньше, чем циклическая частота
0
ω . График такого модулированного
колебания представлен на рис. 5.13,б.
Рис. 5.13
Параметр m, входящий в формулу (5.34), называют глубиной модуляции. Он
определяет разность между максимальным и минимальным значениями
амплитуды модулированного колебания
(
)
()
max min
max min
AA
x1
AA
−
=<
+
. (5.35)
Амплитудно-модулированное колебание можно представить в виде суммы
трех гармонических колебаний с циклическими частотами
0
ω ,
0
ω −Ω и
0
ω
+
Ω
(
0
щ называют несущей частотой, а две остальные – боковыми частотами) и
с амплитудами
0
A , 2/
0
mA и 2/
0
mA соответственно
() ()
()
()
()
000 0 0 0 0 0 0
11
sin
ωsinω sinω
22
= + + −Ω+ + +Ω+xA t mA t mA t
ϕ
ϕϕ
. (5.36)
Модулированные колебания применяются для передачи информации с
помощью электромагнитных волн радио - или оптического диапазонов, а также
акустических волн. Любая передающая радиостанция, работающая в режиме
амплитудной модуляции, излучает не одну частоту, а спектр частот – несущую
и две боковые. Если модулирующий сигнал более сложный, то вместо двух
боковых частот будут две боковые
полосы. Поэтому каждая передающая
станция занимает определенный частотный интервал, для радиовещания
ширина боковой полосы составляет 10 кГц.
5.8. Спектральное представление различных сигналов
Как известно, общий подход к анализу сложных процессов и явлений
заключается в их разложении на более простые процессы и явления. Этот же
подход может быть применен к анализу
периодических процессов, учитывая,

23
что наиболее простыми среди периодических функций являются
гармонические колебания.
Любое сложное колебание можно представить в виде суммы гармонических
колебаний, их называют гармониками. Разложение сложного колебания на
гармонические колебания (без учета их фаз) называется спектральным
разложением. Диаграмма, изображающая зависимость амплитуды каждой
гармоники от ее частоты, называется спектром сложного колебания или
спектром
амплитуд.
В качестве примера приведем спектры амплитуд для различных
периодических колебаний
)(tf
.
1. Гармоническое колебание с частотой
0
ω :
(
)
(
)
0
=cosω
f
tA t.
Спектр амплитуд для такой функции представляет собой одну линию
амплитуды А на частоте
0
ω (рис. 5.14,а).
2. Биения (частный случай одинаковых амплитуд складываемых колебаний -
AAA ==
21
):
()
12
112 2
ωω
ω
cos ω cosω 2 cos cos
22
+
∆
=+ =
f
tA tA t A t t
.
Спектр амплитуд представляет собой две близко расположенные линии c
амплитудами А и с частотами
1
щ
и
2
щ
(рис. 5.14,б).
3. Амплитудно-модулированное колебание:
(
)
(
)( )
000
1cossinω=+ Ω +ft A m t t
ϕ
.
Как следует из формулы (5.36), спектр этого колебания представляет собой
три линии с частотами
0
ω −Ω ,
0
ω и
0
ω
+
Ω и с амплитудами 2/
0
mA , А и 2/
0
mA
соответственно (рис. 5.14,в).
Рис. 5.14
4. Наиболее общий случай: произвольная периодическая функция
)(tf
.
В этом случае спектр амплитуд не будет таким простым, как в приведенных
выше примерах. В математике доказывается, что при условиях, которые

24
обычно выполняются в физических задачах, периодическую функцию
)(tf
с
периодом Т (см., например, рис. 5.1,б) можно представить в виде суперпозиции
бесконечного числа гармонических колебаний, частоты которых образуют
дискретную последовательность. Эти частоты кратны основной циклической
частоте
ω (
T
π
=ω
2
) изменения функции
)(tf
и принимают значения
ω, 2ω, 3ω, 4ω и т.д. Такая сумма называется рядом Фурье или гармоническим
разложением сложного периодического колебания.
() ()
0
1
cos ω
2
∞
=
=+ −
∑
nn
n
A
ft A nt
ϕ
, (5.37)
где коэффициенты Фурье
nn
A
ϕ
,
определяются видом функции
)(tf
.
Совокупность величин
n
A называется спектром амплитуд функции
)(tf
, а
совокупность
n
ϕ
– спектром фаз. Слагаемое ряда Фурье с частотой ω называют
первой (основной) гармоникой, а остальные – высшими (второй, третьей и
т.д.)
гармониками или обертонами функции
)(tf
.
В качестве примера приведем спектр амплитуд пилообразной периодической
функции
)(tf
(она приведена на рис. 5.1,б), временная зависимость которой
описывается следующим образом:
,...3,2,1,0,/))1(()(:)1(
0
=−+=+<< nTtTnxtfTntnT
.
Можно показать, что коэффициенты Фурье в этом случае будут равны
()
0
π=
n
A
xn
,
р 2
n
ϕ
=
Спектр амплитуд для такой периодической функции приведен на рис. 5.14,г.
Он представляет собой бесконечный дискретный набор гармоник, амплитуды
которых убывают обратно пропорционально номеру гармоники.
5. Функция
)(tf
не является периодической функцией времени. В этом
случае она также может быть представлена в виде бесконечной суммы
гармонических колебаний, но в этом случае их частоты образуют
непрерывную последовательность. Эта сумма будет записываться в виде
интеграла Фурье
() () () ()
()
0
11
tt ωcosω ω ω
2π2π
∞∞
−∞
== −
∫∫
it
f
tfedA td
ω
ϕ
, (5.38)
() ()
ωωω
∞
−∞
=
∫
it
FFed
ω
,
() () ()
(
)
()
Im ω
ω2 ω,tgω
Re ω
−
==
F
AF
F
. (5.39)
Величины
()
ωA и
()
ω
ϕ
представляют амплитудный спектр и фазовый
спектр функции
)(tf
. Функцию
(
)
ωF
называют Фурье-образом функции
)(tf
,
ее комплексным спектром или просто спектром
)(tf
. Функция
()
ωF
полностью
определяет функцию
)(tf
и эквивалентна ее амплитудному и фазовому
спектрам. При записи формул (5.38) и (5.39) была использована формула
Эйлера для комплексного представления гармонического колебания
cos sin
±
=±
i
ei
α
α
α
, (5.40)
где
i
– мнимая единица:
1−=i
.

25
Нужно помнить, что комплексная форма записи гармонических колебаний
удобна при проведении расчетов или математических выкладок. При переходе
от комплексной формы записи к реальной функции берут вещественную часть
комплексного числа
() ()
ω
0
1
Re ωω
π
∞
−
=
∫
it
f
tFed. (5.41)
В качестве примера непериодической функции
)(tf
можно привести
изолированный прямоугольный импульс высотой
0
x , ограниченный интервалом
времени
τ
(рис. 5.14,д). Спектр амплитуд такого импульса является сплошным
(рис. 5.14,е), причем
()
(
)
()
0
sin ωτ 2
ω2 , ω0
ωτ 2
Ax==
τϕ
. (5.42)
.
Таким образом,
периодические функции характеризуются дискретными
спектрами амплитуд, а непериодические – непрерывными спектрами
амплитуд
.
Ограниченные во времени непериодические функции представляют
собой
импульсные сигналы (их еще также называют импульсами), для
которых можно ввести понятия продолжительности импульса
∆
τ
и ширины ω
∆
спектра
импульса. Продолжительность импульса
∆
τ
– это промежуток
времени, в течение которого амплитуда импульса существенно отличается от
нуля, а
ширина
ω∆
спектра импульса – это интервал частот, на котором
амплитуда спектра существенно отличается от нуля.
Можно показать,
что ширина ω
∆
спектра импульса обратно
пропорциональна его продолжительности
∆
τ
. Действительно, на
рассмотренном выше примере прямоугольного импульса можно записать
приближенное равенство
ω2π
∆
⋅∆ ≈
τ
, (5.43)
где за ширину
ω∆ спектра была принята частота, при которой впервые
амплитуда спектра обращается в ноль:
11
ω2π1 ωω2π,
=
⇒∆ = = ∆ =
τ
τττ
(см.
рис.5.14,е). Равенство (5.43) часто используется для приближенной оценки
ширины частотного спектра различных импульсов.
В заключение параграфа отметим, что исследование спектрального состава
временных процессов, представление их в виде набора самого простого вида
колебаний – гармонических колебаний, имеют ряд неоспоримых преимуществ
и поэтому широко применяются во многих разделах не только физики, но
и
других естественных наук. К таким преимуществам можно отнести, например,
простую и наглядную классификацию временных процессов по спектру их
амплитуд; методику анализа распространения различных сигналов в средах по
изменению частотного спектра сигнала; целенаправленное изменение
временных сигналов по изменению их частотного спектра и т.д.

26
5.9. Затухающие колебания
5.9.1. Дифференциальное уравнение затухающих колебаний, его
решение
Затухающие колебания происходят в замкнутой механической системе
(
ВНЕШ
F
=0), в которой имеются потери энергии на преодоление сил
сопротивления (β ≠ 0) или в закрытом колебательном контуре (U
ВНЕШ
=0), в
котором наличие сопротивления R приводит к потерям энергии колебаний на
нагревание проводников (β ≠ 0).
В этом случае общее дифференциальное уравнение колебаний (5.1)
примет вид
2
0
2βω 0
′′ ′
++=xxx. (5.44)
Решением уравнения (5.44) являются затухающие колебания
()
(
)
β
00
cos ω
−
=−
t
m
qt qe t
ϕ
, (5.45)
где амплитуда колебаний
(
)
A
t убывает со временем по
экспоненциальному закону
()
β
0
,
−
=
=
t
m
qt Ae A q
(5.46)
а циклическая частота затухающих колебаний
З
ω
определяется формулой
2
2
0З
β−ω=ω
, (5.47)
из которой следует, что
30
ωω
<
.
Графики зависимости от времени t амплитуды
(
)
A
t и заряда
)(tq
на
обкладках конденсатора приведены на рис. 5.15.
Рис. 5.15
В случае механической системы по табл. аналогий 5.1 можно получить
уравнения, подобные уравнениям (5.44), (5.45):
2
0
2βω 0
′′ ′
+
+=xxx
, (5.48)
27
(
)
(
)
β
30
cos ω
−
=+
t
m
xt xe t
ϕ
. (5.49)
Отметим только, что для получения затухающих колебаний вида (5.49)
необходимо, чтобы сила сопротивления, действующая в механической системе,
была пропорциональна скорости движения тела
СОПР
′
=
−=−
XX
Frrx
ν
. (5.50)
Только в этом случае получается дифференциальное уравнение
затухающих колебаний в виде (5.48). Формула (5.50) справедлива для
небольших числовых значений скоростей движения тела (м.т.).
В заключение этого параграфа отметим, что из-за уменьшения с течением
времени амплитуды колебаний затухающие колебания не являются
периодическими. Но при малом затухании под
периодом (его также называют
условным периодом) можно понимать минимальное время, за которое
повторяются минимальные значения или максимальные значения
величин, описывающих колебательное движение
(см. рис. 5.15). Аналогично
циклическую частоту затухающих колебаний называют условной
циклической частотой
.
5.9.2. Характеристики, вводимые для описания
затухающих колебаний
Рассмотрим кратко величины, вводимые для описания затухающих
колебаний.
1.Критическое сопротивление контура
K
R
(критический коэффициент
сопротивления среды
K
r
). Критическое сопротивление контура – это такое
сопротивление, при котором в контуре начинается
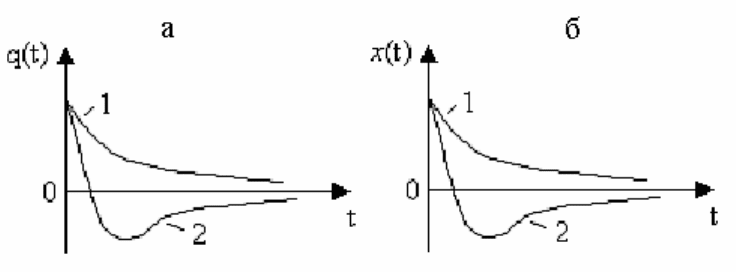
апериодический разряд. В
этом случае колебания в контуре отсутствуют, заряд на обкладках
конденсатора убывает монотонно до нуля (кривая 1 на рис. 5.16), или, пройдя
один раз положение равновесия, заряд конденсатора в итоге монотонно будет
убывать до нуля (кривая 2 на рис. 5.16).
Рис. 5.16
Убывание заряда
q
, смещения
x
тела в механической системе по кривым 1
или 2, либо по кривой, расположенной между ними, зависит от начальных
условий. Например, если поместить физический маятник в жидкую вязкую
среду и, отклонив его от положения равновесия, отпустить без начальной

28
скорости, то тогда смещение
)(tx
маятника будет изменяться по кривой 1 (рис.
5.16,б). Если же отпустить маятник с начальной скоростью, направленной к
положению равновесия, то тогда его смещение может со временем изменяться
по кривой 2 (рис. 5.16,б), т.е. он пройдет один раз положение равновесия, затем
отклонится, и после этого в итоге будет монотонно приближаться к
положению
равновесия.
Выведем формулу для критического сопротивления контура
K
R
через
параметры контура L и C. При увеличении сопротивления
R
угловая частота
затухающих колебаний будет уменьшаться, а период колебаний Т
З
будет
возрастать, и для сопротивления
R
, равного
K
R
, можно записать
K
RR =
:
∞=
ω
π
==β−ω=ω
З
З
2
2
0З
2
,0 T
,
L
R
LC
K
2
1
0
=⇒β=ω ,
C
L
R
K
2=
. (5.51)
Для
K
RR ≥
в контуре наблюдается апериодический разряд, а при
K
RR
<
в
контуре происходят затухающие колебания.
По таблице аналогий (см. табл. 5.1) для критического коэффициента
сопротивления среды
K
r
можно записать (L
→
m, 1/С
→
к)
mkr
K
2=
. (5.52)
2. Время релаксации τ – это время, в течение которого амплитуда колебаний
убывает в e раз (e-основание натурального логарифма):
()
()
τ
=
−
At
e
At
,
(
)
β
0
−
=
⇒
t
At Ae
β
=τ
1
. (5.53)
За время релаксации в системе совершается N
e
полных колебаний:
ЗЗ
1
TT
N
e
β
=
τ
=
(5.54)
3. Логарифмический декремент затухания δ равен натуральному логарифму
отношения двух амплитуд, взятых через период:
e
N
T
TtA
tA
ln
1
)(
)(
З
З
=β=
+
=δ
. (5.55)
4. Добротность Q системы можно ввести как величину, определяющую
потери энергии колебаний системы за один условный период колебаний,
)()(
)(
2
З
TtWtW
tW
Q
+−
π=
. (5.56)
Полная энергия колебаний пропорциональна квадрату амплитуды колебаний
и поэтому выражение (5.56) можно записать в следующем виде:
(
)
() ( )
2
22
δ
3
2
π
2π
1
−
==
−+ −
i
At
Q
At AtT e
. (5.57)
Из формулы (5.56) следует, что чем выше добротность Q системы, тем
медленнее в ней затухают колебания.
Приведем ориентировочные значения Q для различных систем:

29
1) колебательный контур на радиочастотах (ω ~ 10
6
рад/с): Q ~ 100; 2) полый
резонатор диапазона сверхвысоких частот (ω ~ 10
11
рад/с): Q ~ 10
5
; 3) камертон:
Q ~ 10
4
; 4) колебания кварцевой пластины: Q ~ 10
5
; 5) излучение атома как
колебательной системы: Q ~ 10
7
.
Как видно, для применяемых на практике систем Q
≥
100, т.е. для них
выполняются
условия малого затухания:
003
1 βω,ωω, ,δβ 1⇒≅== QTTT .
Тогда из формулы (5.57) получим (
1,1 <<+≈ xxe
x
)
0
ω
πππ
πN
δβ T 2β
e
Q
T
== = = =
τ
. (5.58)
Для добротности механической системы и колебательного контура из
формулы (5.58) в условиях малого затухания можно получить следующие
формулы:
r
m
r
k
r
mk
r
r
Q
k 0
0
2
ω
=
ω
===
,
R
L
RCR
CL
R
R
Q
K
0
0
1
2
ω
=
ω
===
. (5.59)
5.10. Вынужденные колебания
5.10.1. Уравнения вынужденных колебаний, их решения
Под
вынужденными колебаниями понимают колебания, происходящие в
системе в результате внешнего воздействия (внешней силы или внешнего
напряжения), изменяющегося со временем по гармоническому закону. При
этом колебания в системе происходят на циклической частоте ω внешнего
воздействия, а амплитуды колебаний различных величин в системе будут
зависеть от этой частоты.
Рассмотрим дифференциальное уравнение и его решение
для вынужденных
колебаний, происходящих в колебательном контуре под действием внешнего
напряжения, изменяющегося по гармоническому закону
tUU
m
ω
= cos
ВНЕШ
. (5.60)
В этом случае дифференциальное уравнение (5.1) примет следующий вид:
()
2
0
2βω cosω
′′ ′
++=
m
U
qqq t
L
. (5.61)
Известно, что решением этого уравнения является следующее выражение
() ( )
(
)
β
00
cos ωcosω
−
=−=+
t
mm
qt qe t q t
ϕϕ
. (5.62)
Из формулы (5.62) следует, что первое слагаемое представляет собой
уравнение свободных затухающих колебаний системы и амплитуда этих
колебаний с течением времени уменьшается. Если взять время t, большее
времени установления стационарного режима колебаний в контуре (t > t
уст
), то
тогда в выражении (5.62) останется только второе слагаемое (первым

30
слагаемым можно пренебречь), которое представляет собой уравнение
вынужденных колебаний заряда q на обкладках конденсатора
t > t
уст
: )cos()(
ψ
−
ω
=
tqtq
m
. (5.63)
Аналогичные уравнения можно записать для напряжения U
C
на конденсаторе
и силы тока I в контуре
)cos( ψ−ω== tU
C
q
U
CmC
,
()
π
sin ωψ cosωψ
2
⎛⎞
′
==− − = −+
⎜⎟
⎝⎠
mm
Iq I t I t . (5.64)
Как уже отмечалось, амплитуды колебаний этих величин зависят от частоты
ω
внешнего напряжения, такие зависимости называют резонансными
кривыми
: )(ω=
mm
qq ,
(
)
ω=
Cm Cm
UU , )(
ω
=
mm
II .
Выведем формулы для этих зависимостей. Для этого используем формулу
Эйлера (5.40) для комплексной формы записи гармонического колебания.
() ( )
(
)
ωψ
cos ωψ
−
=−=
it
mm
qt q t qe ,
(
)
ωψ
ω
−
′
=
it
m
qiqe ,
(
)
ωψ
2
ω
−
′′
=−
it
m
qqe
,
ω
cos ω==
it
ВНЕШ mm
UUtUe.
Подставим эти выражения в формулу (5.61):
()
ωψ 2 2 ω
0
ω2βωω
−
−+ + =
it i it
m
m
U
qe e i e
L
,
()
()
22 ψ
0
ωω 2βω cosψ sinψ−+ = = +
i
mm m
m
UU U
qiei
LL L
.
Два комплексных числа равны, если будут равны их вещественные и мнимые
части, поэтому
ψ=ω−ω cos)(
2
2
0
L
U
q
m
m
,
ψ=βω sin2
L
U
q
m
m
. (5.64а)
Возведем каждое уравнение (5.64а) в квадрат, сложим их и получим
2222
2
0
4)( ωβ+ω−ω
=
L
U
q
m
m
. (5.65)
Разделим уравнения (5.64а) одно на другое, что приводит к формуле
2
2
0
2
ω−ω
β
ω
=ψtg
. (5.66)
Используя выражение (5.65), запишем
()
2
22 22
0
ωω 4βω
==
−+
mm
Cm
qU
U
C
LC
. (5.67)
2222
2
0
4)( ωβ+ω−ω
ω
=ω=
L
U
qI
m
mm
. (5.68)
Рассмотрим подробнее резонансные кривые для амплитуды напряжения на
конденсаторе
()
ω
Cm
U
и амплитуды силы тока )(
ω
m
I в контуре.
