Валиев Ф.С., Гребенюк Г.И. Сопротивление материалов: основы теории и примеры решения задач (часть 2)
Подождите немного. Документ загружается.


41
ρ(x) – функция радиусов кривизны.
М(х) – функция изгибающих моментов.
Е(х) – функция модуля упругости материала балки;
I
Z
(х) – функция главного центрального момента инерции
сечения относительно оси, перпендикулярной к плоскости дей-
ствия сил.
Произведение E(х)I
Z
(х) называется жесткостью стержня
при изгибе.
Рис 3.1
Будем полагать в дальнейшем, что соотношение (3.1) при-
менимо при рассмотрении прямого поперечного изгиба (Q
≠ 0,
M(x)
≠ const).
Для аналитического решения задачи определения переме-
щений сечений балки v(x),
(х),
θ
(рис 3.1) используется извест-
ное из математического анализа выражение кривизны плоской
кривой:
χ
(х) =
23/2
v"
,
[1 ( v ') ]
+
(3.2)
где v(х) - функция вертикальных перемещений (проги-
бов) сечений балки;
(х)
θ
- функция углов поворота сечений балки.
Учитывая (3.2), получим уравнение, которое называется точным
дифференциальным уравнением оси изогнутой балки:
23/2
v"(х) М(х)
[1 ( v '( х)) ] E(х)I(х)
=
+
(3.3)
В строительных конструкциях нагружение балок является,
как правило, монотонным, и на величины прогибов накладыва-
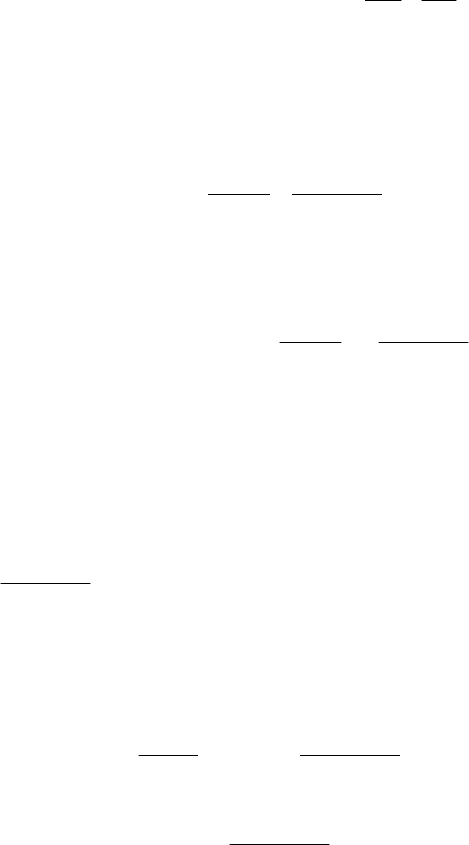
42
ются жесткие ограничения. (|v|max
≤
(
11
200 800
÷ ))L, L – пролет
балки. Поэтому величины
v (x) tg( (x)) (x)
′
=
θ≈θявляются ма-
лыми (значительно меньше единицы), и в левой части уравнения
(3.3) можно пренебречь квадратом первой производной функ-
ции прогибов. В результате получим приближенное дифферен-
циальное уравнение оси изогнутой балки:
2
2
z
d v(x) M(x)
v''(х)
dx E(х)I (х)
== (3.4)
В случае, когда ось У направлена вверх, знаки v(x)
′
′
и М(х)
совпадают. Если ось “У” направлена вниз, уравнение (3.4) пре-
образуется к виду:
2
2
z
d v(x) M(x)
v(х)
dx E(x)I (x)
′′
==− (3.5)
Уравнения (3.4), (3.5) – обыкновенные дифференциальные
уравнения второго порядка, приведенные к квадратурам. По-
этому метод непосредственного интегрирования заключается,
по сути, в двукратном интегрировании соотношений (3.4), (3.5)
на участках интегрирования и последующем определении по-
стоянных интегрирования. Под участком интегрирования пони-
мается такая протяженность балки, на которой функция:
z
M(x)
E(x)I (x)
не претерпевает изменений.
Пусть по вышеуказанному признаку балка разделилась на n
участков интегрирования. Рассматривая произвольный i-тый
участок, в результате двукратного интегрирования (3.4) полу-
чим выражение для функции
i
v(x),
i
(x)
θ
ii
ii
izi
dv (x) M (x)
(x) dx C
dx E (x)I (x)
≈
θ= +
∫
(3.6)
i
iii
izi
M(x)
v (x) dxdx C x D
E (x)I (x)
=++
∫∫
, i=1,…,n (3.7)
43
Постоянные интегрирования С(i) и D(i), число которых
равно 2n, находятся из кинематических условий закрепления (их
число для статически определимой балки равно 2) и кинемати-
ческих условий стыковки участков. Для стыка
i-того и i+1-ого
участков эти условия имеют вид:
ii i1i1
ii i1i1
v(b) v (a );
(b ) (a ),
++
++
=
θ=θ
(3.8)
где
b
i
, a
i+1
– координаты конца i-того и начала i+1 участков,
b
i
=a
i+1
Общее число условий стыковки равно 2(n–1).
ПРИМЕР 3.1
Дано:
Стальная балка из прокатного двутавра N 20 (ГОСТ 8239 – 89)
(рис.3.2).
Требуется:
Определить прогиб и угол поворота свободного конца консоли.
РЕШЕНИЕ
1. Из условий равновесия определим реакции опоры (за-
щемления):
ΣМ
А
= 0; М
А
– F· l = 0; М
А
= F· l = 15·2 = 30 кН·м.
ΣX = 0; ΣУ = 0; V
А
– F = 0; V
A
= F = 15 кН.
Рис. 3.2
2. Определим жесткость балки EI
Z
:

44
Из таблицы сортаментов для двутавра (ГОСТ 8239–89) номер 20
находим – I
Z
= 1840 см
4
.
Для стали модуль упругости Е = 2·10
8
кПа.
Тогда: EI
Z
= 2·10
8
кПа·1840·10
-8
м
4
= 3680 кН·м
2
.
3. Выбираем начало координат на левом конце балки, в
точке А и для сечения на расстоянии "X" напишем выражение
для изгибающего момента:
М(х) = V
A
·x – M
A
4. Подставим функцию М(х) в дифференциальное уравне-
ние изогнутой оси балки и, выполнив двукратное интегрирова-
ние, получим уравнения для углов поворота и прогибов сече-
ний:
AA
ZZ
M(x) 1
v"(x) (V x M );
EI EI
== ⋅−
(3.9)
2
AA
ZZ
M(x) 1
v'(x) (x) dx C (V x /2 M x) C;
EI EI
=θ = + = − +
∫
(3.10)
Z
M(x)
v(x) dx dx Cx D
EI
=++=
∫∫
32
AA
Z
1
(V x / 6 M x / 2) Cx D.
EI
=
−++ (3.11)
Постоянные интегрирования С и D найдем из кинематиче-
ских граничных условий т.е. из условий закрепления балки.
В начале координат (левый конец балки) имеется жесткое за-
щемление, поэтому там угол поворота и прогиб сечения равны
нулю;
а) x=0 θ = 0;
б) x=0 v = 0;
Условие
а) подставим в уравнение (3.10) и получим: С = 0.
Условие
б) подставим в уравнение (3.11) и получим: D = 0.
Тогда окончательно получаем следующие уравнения для углов
поворота и прогибов сечений балки:
45
22
AA
Z
11
(x) (V x / 2 M x) (15x / 2 30x);
EI 3680
θ= ⋅ − ⋅= −
32 32
AA
Z
11
v(x) (V x / 6 M x / 2) (15 x / 6 30x / 2).
EI 3680
=⋅−⋅= ⋅−
Определим угол поворота и прогиб на правом конце балки
при х=
l =2 м.
222
х
zz
1F F 152
( F ) 0,00815рад
EI 2 2EI 2 3680
=
⋅
θ= − =− =− =−
⋅
l
ll
ll
32 3 3
х 2
zz
1F F F 152
v ( ) 0,01087м.
EI 6 2 3EI 3 3680
==
⋅
= − =− =− =−
⋅
l
lll l
В дальнейшем, для таких типовых балок с одним защем-
ленным концом длиной
l , загруженных с одного конца сосре-
доточенной силой F угол поворота и прогиб свободного конца
можно определять по полученным стандартным формулам:
23
х x
ZZ
FF
;v .
2EI 3EI
==
θ=− =−
ll
ll
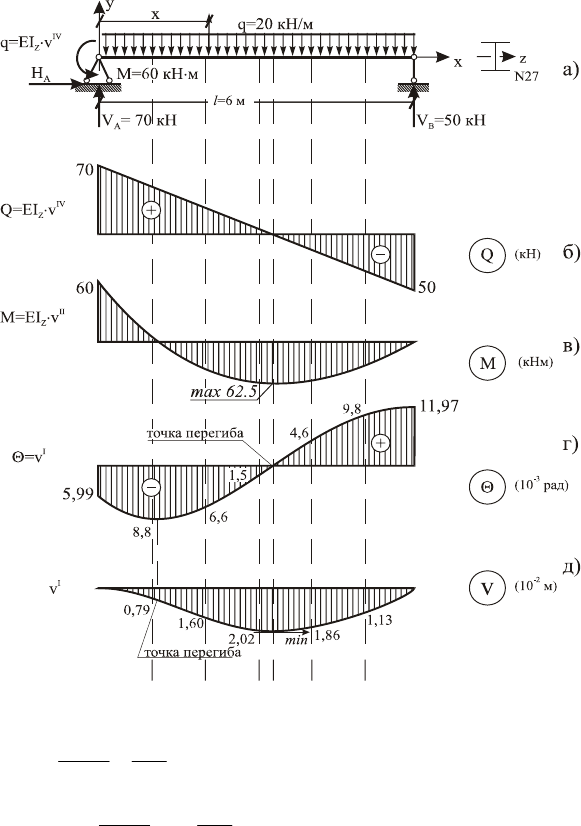
ПРИМЕР 3.2
Дано: Стальная балка (см. рис.3) из прокатного двутавра N27
(ГОСТ 8239-89).
Требуется:
Построить эпюры поперечных сил Q, изгибающих момен-
тов М, углов поворота θ и прогибов сечений
v с учетом диффе-
ренциальных зависимостей между всеми эпюрами.
РЕШЕНИЕ
1. Определим жесткость балки. Из таблицы сортаментов
для двутавра N 27 имеем – I
Z
= 5010 см
4
= 5010·10
-8
м
4
.

46
Модуль упругости для стали примем– Е=2·10
8
кПа.
Тогда – EI
Z
= 2·10
8
·5010·10
-8
= 10020 кН·м
2
.
2.Из уравнений равновесия определяем реакции опор и по-
строим эпюры Q и М.
ΣX = 0; H
A
= 0.
ΣM
A
= 0; V
B
·6 – q·6·3 + M = 0. Отсюда находим V
B
:
B
q63 M 2063 60
V50кН.
66
⋅
⋅− ⋅⋅−
== =
ΣМ
B
= 0; –V
A
·6 + q·6·3 + М = 0.
Отсюда находим V
A
:
А
q63 M 2063 60
V70кН.
66
⋅⋅+ ⋅⋅+
== =
Проверка: ΣУ = 0; V
A
+ V
B
–q·6 = 70 + 50 – 20·6 = 0. По-
строим эпюры Q и М (см. рис. 3 б; и 3 в).
3. Выбираем начало координат на левом конце балки и для се-
чения на расстоянии "x" напишем выражение для изгибающего
момента:
М(х) = V
A
·Х – q·x
2
/2 – М = 70·x – 20·x
2
/2 –60.
4. Подставим функцию М(х) в дифференциальное уравнение
изогнутой оси балки и выполнив двукратное интегрирование,
получим:
47
Рис. 3.3
2
ZZ
M(x) 1
v"(x) (70 x 20 x /2 60).
EI EI
== ⋅−⋅− (3.12)
23
ZZ
M(x) 1
v'(x) dx (70 x /2 20 x /6 60 x) С.
EI EI
=θ= = ⋅ − ⋅ − ⋅ +
∫
(3.13)
48
34 2
ZZ
M(x) 1
v(x) dx dx (70x / 6 20x / 24 60x / 2) СxD.
EI EI
==−−++
∫∫
(3.14)
Постоянные интегрирования С и D найдем из кинематиче-
ских граничных условий, т.е. из условий закрепления балки:
а) x=0, v = 0;
б) x=6 м, v = 0.
Условие а) подставим в уравнение для прогибов (3.14) и по-
лучим: D = 0.
Условие б) подставим в то же уравнение и получим:
34 2
х 6
Z
1
v (706/6 206/24 606/2) C6 0.
EI
=
=⋅−⋅−⋅+⋅=
Откуда:
34 2
Z
160
C (70 6 / 6 20 6 / 24 60 6 / 2) 0,00599
6 EI 10020
=⋅−⋅−⋅=−=−
⋅
рад
Подстановка в уравнение для "θ" координаты левого конца
балки – х=0 показывает, что θ
(Х=0)
=θ
0
= С =–0,00599 рад., а под-
становка в уравнение для "v" координаты х=0 показывает, что
v
(Х=0)
= v
0
= D = 0. Это означает, что постоянная интегрирования
С равна углу поворота в начале координат, a "D" – соответст-
вует прогибу в начале координат, т.е. геометрический смысл
постоянных интегрирования заключается в том, что С= θ
0
, а
D = v
0
.
Перепишем в окончательном виде уравнения (3.13) для опреде-
ления θ и (3.14) для определения v:
23
1
(70 x / 2 20 x / 6 60 x) 0,00599.
10020
θ= ⋅ − ⋅ − ⋅ − (3.15)
34 2
1
v (70 x / 6 20 x / 24 60 x / 2) 0,00599 х.
10020
=⋅−⋅−⋅−⋅
(3.16)
49
Для определения угла поворота какого-либо сечения, под-
ставим в уравнение (3.15) координату этого сечения, напри-
мер, для определения угла поворота сечения на правом конце
балки подставим – x=6м.:
23
(Х 6)
1
(70 6 / 2 20 6 / 6 60 6) 0,00599
10020
180
0,00599 0,01197рад.
10020
=
θ= ⋅ −⋅ −⋅− =
=− =
Для определения прогиба сечения, например, посередине
пролета, подставим в уравнение (3.16) координату этого сече-
ния - x = 3 м.
34 2
(х 3)
1
v (703/6 203/24 603/2) 0,005993
10020
22,5
0,01797 0,02022м.2,02см.
10020
=
=⋅−⋅−⋅−⋅=
−
=− =− =−
Подставляя в формулы (3.15) и (3.16) значения
x через 1
метр, вычислим в этих сечениях углы поворота и прогибы.
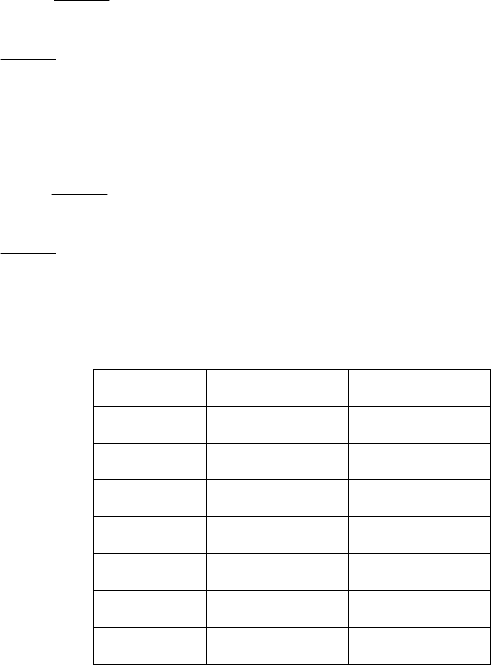
Результаты вычислений представлены в следующей таблице:
x(м) θ(рад) v(м)
0 –0,00599 0
1 –0,00882 –0,00790
2 –0,00666 –0,01597
3 –0,00150 –0,02022
4 0,00466 –0,01863
5 0,00981 –0,01127
6 0,01197 0
По этим результатам, под эпюрами Q и М, строим эпюры θ
и v, соединяя точки между собой с учетом дифференциальных
зависимостей между всеми эпюрами:
q = dQ/dx = d
2
М/dx
2
= EI
Z
·d
3
θ/dx
3
= EI
Z
·d
4
v/dx
4
, (см. рис.3.3г; д).

50
3.2. Метод начальных параметров
Метод непосредственного интегрирования позволяет решать
задачи определения перемещений при любом законе изменения
жесткости сечений балки. В случае, когда балка имеет постоян-
ную жесткость (EI
z
=const) и несколько грузовых участков, его
применение становится нерациональным, так как для определе-
ния постоянных интегрирования зачастую требуется составлять
и решать достаточно громоздкую систему линейных алгебраи-
ческих уравнений. Этих трудностей можно избежать, если при
составлении и интегрировании на участках дифференциальных
уравнений упругой оси изогнутой балки придерживаться сле-
дующих правил (правил Клебша):
1. Начало общей для всех участков системы координат не-
обходимо располагать в центре тяжести левого (или пра-
вого) концевого сечения балки.
2.
Распределенную нагрузку продолжать (с сохранением
ее характера) до конца балки, противоположному началу
координат. При этом несуществующая часть нагрузки
уравновешивается нагрузкой обратного направления
(см. рис. 3.4).
3.
Сосредоточенный момент M
i
, входящий в выражение
для правой части (3.4), записывать с множителем
Mi
(x a )−
0
, здесь a
Mi
– координата точки приложения мо-
мента.
4.
При интегрировании выражения типа
n
(x a) dx− скобки
не раскрывать, т.е.
n1
n
(x a)
(x a) dx
n1
+
−
−=
+
∫
(3.17)
Опуская доказательство, отметим, что при соблюдении вы-
шеперечисленные правил постоянные интегрирования на участ-
ках соответственно равны друг другу, и число их сокращается
до двух:
С(1)=С(2)=…=С(n)=C; D1= D2=…= D n= D (3.18)
