Угльницкий Г.А. Иерархическое управление устойчивым развитием

Подождите немного. Документ загружается.

Глава 2. Методы и модели иерархического управления 51

ства). Положительный квадрант образован социальными позициями,

которые занимают стабильные, респектабельные, «добропорядочные»

члены («столпы») общества, ведущие себя в соответствии с существую-

щими социальными нормами и получающие за это заслуженное возна-

граждение. Социальные позиции из отрицательного квадранта облада-

ют негативным, «взрывным» потенциалом: занимающим эти позиции

индивидам уготована участь отверженных, «париев» общества, и их со-

циальное поведение колеблется от глухой покорности до «беспощадного

и бессмысленного» бунта. Позиции из остальных квадрантов имеют мар-

гинальную природу: находящиеся в них индивиды стремятся быть ува-

жаемыми членами общества, но общество не отвечает им взаимностью;

их усилия в одном социальном поле не ведут к росту капитала в других

полях. Социальный статус этих позиций может быть как положительным,

так и отрицательным, что ведет к неустойчивости соответствующих со-

циальных групп.

Из рис. 2.1.1 видна еще одна закономерность: социальные позиции,

симметричные относительно начала координат, имеют одинаковую дли-

ну, а их проекции равны по величине, но противоположны по знаку. По-

этому занимающие их индивиды как бы «равновелики» каждый в своем

мире, ценности которых противоположны. Как пишет Бурдье, «эффект

гетто есть полная противоположность эффекту клуба. В то время как ши-

карные кварталы, функционирующие как клубы, основанные на актив-

ном исключении нежелательных лиц, символически посвящают каждого

из своих обитателей ... гетто символически разлагает каждого из своих

обитателей» (Бурдье 1993:49).

Любой социальный субъект определенным образом «организован»

и входит в состав структурированных организаций более высокого по-

рядка. Большинство существующих социальных систем: от микро- до

метасоциального масштаба — строятся по иерархическому принципу,

хотя в процессе становления современной постиндустриальной гума-

нистической цивилизации зарождаются и отвоевывают «свое место под

солнцем» так называемые «сотовые» (закольцованные) организационные

структуры (Хруцкий 1993). «Пирамидальными» до сих пор остаются со-

циальные структуры семьи, всех административных систем, государств,

а также мирового сообщества (Уоллерстейн 1992). Чем «пирамида» от-

личается от «сот», понятно — наличием пресловутой «иерархии», то есть

вертикального взаиморасположения отдельных субъектов и целых соци-

альных слоев, называемого социальной стратификацией. Считается, что,

будучи членом множества иерархически структурированных организа-

ций, индивид в то же время принадлежит к определенному общественно-

му слою, причем расслоение (стратификация) по различным признакам:

52 Иерархическое управление устойчивым развитием

политическому, экономическому, профессиональному и другим (Соро-

кин 1992) — в каждом обществе приобретает свое специфическое значе-

ние, играя первостепенную или второстепенные роли в «строительстве

общей пирамиды» социума.

В советском обществе приоритетную стратификационную роль иг-

рал критерий идеологической приверженности, в современном россий-

ском «переходном» обществе возросла роль «капитала», то есть, в первую

очередь, финансового статуса, а в недалекой исторической перспективе,

очевидно (как и во всех эффективных сообществах современного соци-

ального типа), ведущей станет роль образования и высокой профессио-

нализации.

Поскольку стратификационные основания «общественной пирами-

ды» в целом могут существенно отличаться от принципов иерархического

строения отдельного локального сообщества или конкретной организа-

ции, понятно, что отношение иерархии между двумя индивидами в некой

организационной структуре может характеризоваться иначе, чем в сис-

теме общественного расслоения в целом.

Организационная структура большинства социальных сообществ, как

правило, пирамидальна, и в зависимости от конфигурации слоевой струк-

туры топологически представлена одной (с треугольным профилем) или

двумя «пирамидами», которые соединяются либо своими основаниями

(профиль — ромб), либо вершинами (профиль — «песочные часы»). Лю-

бая социальная иерархия носит кратический (властно-соподчиняющий)

характер (Мостовая 1996), поскольку распределение субъектов (слоев)

в ней связано с нарастанием определенного социального качества, кото-

рое П. Бурдье (1993) определяет как «социальный капитал», а Р. Даль —

как любую возможность влиять (то есть распространять свою волю на

нижестоящих в иерархии, используя их ресурсы, возможности и орга-

низационную некомпетентность). Исследователь социального господ-

ства О. Массинг в этом смысле очень точно характеризует социальные

отношения как «асимметрически структурированные связи», в которых

каналы социального воздействия «сверху вниз» активизированы в значи-

тельно большей степени, нежели «снизу вверх». Это тоже, в принципе,

не исключено, но требует своей особой организации для получения за-

метного эффекта. В.И. Ленин писал: «Дайте мне организацию револю-

ционеров, и я переверну Россию», а современный глобалист И. Уоллер-

стейн призывал сырьедобывающие государства мировой экономической

периферии объединяться, противодействуя экспансии технологических

монополистов.

Чтобы моделировать совокупность элементов социальной организа-

ции и связей между ними, выражающих отношения иерархии (суборди-

Глава 2. Методы и модели иерархического управления 53

нации, соподчиненности), естественно использовать для ее формального

представления конечный связный ориентированный граф (Робертс 1986)

D(Y,Z), где Y = {y

,...,y

} — множество вершин, соответствующих элемен-

там организации; Z = {(y

)} — множество дуг, обозначающих отношения

соподчиненности между элементами: дуга (y

) проводится в том и толь-

ко в том случае, когда элемент y

является непосредственным начальни-

ком элемента y

в организации D. В дальнейшем мы будем отождествлять

организационную структуру и представляющий ее орграф D.

Напомним, что путем в орграфе (или каналом передачи волевого:

управляющего, регулирующего, координирующего и контролирующе-

го — социального воздействия в организации) называется последова-

тельность вершин и дуг с учетом ориентации: y

), y

, (y

),..., y

k+1

), y

k+1

. Длиной пути называется число входящих в него дуг (сопод-

чиненных элементов социальной системы); так, выписанный путь имеет

длину k. Путь от вершины до самой себя всегда существует и имеет ну-

левую длину.

Будем говорить, что вершины u,v из множества Y связаны отношени-

ем строгой иерархии (u > v), если существует путь ненулевой длины от u

к v. Вершина u называется в этом случае предком v, a вершина v — потом-

ком u. Таким образом, если u > v, то индивид u является либо непосред-

ственным, либо косвенным («вышестоящим») начальником (авторитет-

ной, статусной фигурой с признанным, легитимным правом «влиять» на)

индивида v. Естественно считать, что если u — непосредственный или

косвенный начальник v, то обратное невозможно. Можно возразить, что

реальные социальные структуры предоставляют множество примеров

подобных ситуаций, когда иерархическая структура становится амбива-

лентной, двойственной за счет наложения зависимостей, возникающих

в недрах функциональной структуры, но на основе внефункциональных

факторов: родственных, сексуальных, товарищеских или имиджевых

связей, например, при угрозе шантажа — формализация таких ситуаций

будет предложена ниже. Случаи u > u, когда индивид является начальни-

ком над самим собой, крайне редки и их также можно не рассматривать

в модели. Поэтому в нашей модели D не содержит контуров (т. е. путей,

в которых вершины не повторяются и начальная вершина совпадает с ко-

нечной) и петель (т. е. дуг вида (u,u)).

Таким образом, бинарное отношение строгой иерархии Н на множест-

ве элементов организации (вершин орграфа) Y, т. е. множество пар (u,v),

где u,v ∈ Y, обладает следующими свойствами:

— иррефлексивность: ∀u ∈ Y (u,u) ∉ H;

— асимметричность: ∀u,v ∈ Y (u,v) ∈ H => (v,u) ∉ H;

— транзитивность: ∀u,v,w (u ≠ w) (u,v) ∈ H & (v,w) ∈ H => (u,w) ∈ H.

54 Иерархическое управление устойчивым развитием

Рассмотрим множество ℜ всех разбиений R множества вершин Y бес-

контурного орграфа

D = (Y,Z): R = {L

, L

, ..., L

}, где

Y = L

∪ L

∪ ... ∪ L

, L

∩ L

= ∅, L

, L

∈ 2

Будем считать, что ∅ ∉ ℜ. Назовем элементы разбиения L

слоями,

i = 1,...,m, где m — число слоев в разбиении R (1 ≤ m ≤ n). Число вершин

в слое L

обозначим n

, так что

+ ... + n

= n, 1 ≤ n

≤ n, i=1,...,m, n — число вершин D.

Расслоением S бесконтурного орграфа D назовем пару <R,π(m)>, где

R ∈ ℜ, π(m) — перестановка множества номеров слоев {1,...,m}. Обозна-

чим множество всех расслоений через ℘ . Расслоение < {y

,..., y

},1 > на-

зовем тривиальным, а расслоения <{{y

},{y

},...,{y

}}, π(m) > — одноэле-

ментными.

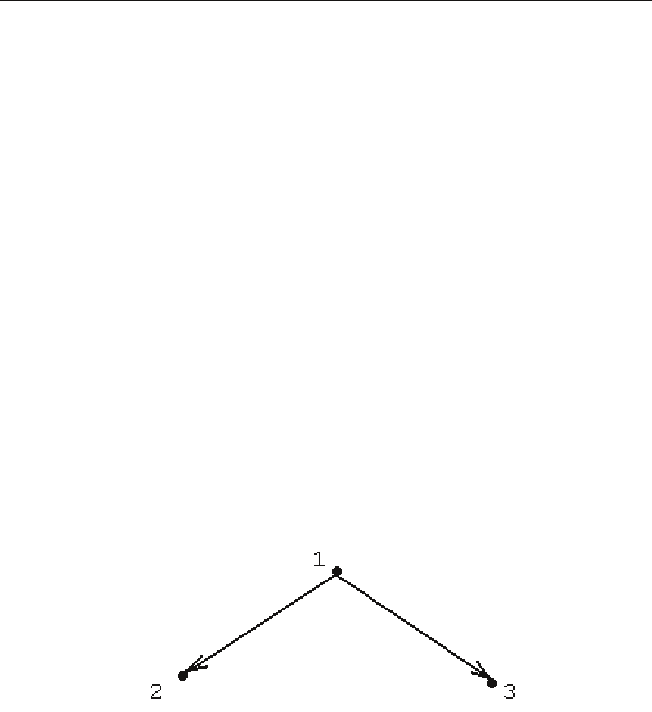
На рис. 2.1.2 изображен бесконтурный орграф D = (Y,Z), Y = {1,2,3},

Z = {(1,2),(1,3)}. Здесь ℜ = {{1,2,3}, {{1},{2,3}}, {{1,2},{3}}, {{1,3},{2}},

{{1},{2},{3}}};

℘ = {{1,2,3}, {{1},{2,3}}, {{2,3},{1}}, {{1,2},{3}}, {{3},{1,2}}, {{1,3},{2}},

{{2},{1,3}}, {{1},{2},{3}}, {{1},{3},{2}}, {{2},{1},{3}}, {{2},{3},{1}}, {{3},{1},{2}},

{{3},{2},{1}}}.

Легко придать содержательный смысл разбиению R

= {{1},{2,3}}, раз-

деляющему организацию на начальника (слой L

) и двух подчиненных

(слой L

). Этому разбиению соответствуют два расслоения S

= {{1},{2,3}} =

= {L

} и S

= {{2,3},{1}} = {L

Как считает А. Пригожин: «О структуре неформальной группы мож-

но говорить и как об отражении более общей социальной структуры,

поскольку каждый ее член является представителем и другой, внеорга-

низационной социальной категории, группы (экономической, демогра-

фической, политической и т. д.). При этом на уровне группы это разли-

чие обычно непосредственно не обнаруживается, а преломляется в других

Рис. 2.1.2. Бесконтурный орграф

Глава 2. Методы и модели иерархического управления 55

формах, порожденных личностными контактами. Тем не менее методо-

логически неправомерно отрывать анализ первичных социальных про-

цессов от макроструктуры общества» (Пригожин 1980).

Как определено выше, социальная стратификация по некоторому при-

знаку может быть записана в виде M = {K

, K

, ..., K

}, где K

— множество

членов общества, образующих j-й слой стратификации М.

Множество Y членов организации со структурой D = (Y,Z) является

подмножеством множества всех членов общества Х. Расслоение S орга-

низации порождается социальной стратификацией М, если:

1) любой слой расслоения S входит только в один слой стратифика-

ции М;

2) никакие два слоя S не входят в один и тот же слой стратифика-

ции М.

Очевидно, для стратификации общества в целом по критерию (основа-

нию) М существует (и притом единственное) порождаемое ею расслоение

S любой организации как подмножества общества. В частности, расслое-

ние S может оказаться тривиальным, когда все члены организации попа-

дают в один и тот же слой стратификации М, или одноэлементным, когда,

напротив, все члены организации принадлежат различным слоям М.

Расслоение S = < R, π(m) > назовем:

— расслоением с горизонтальными связями, если

∃ L

∈ R ∃ u,v ∈ L

: (u,v) ∈ Z;

— расслоением с обратными связями, если

∃ L

∈ R ∃ u ∈ L

, v ∈ L

: (u,v) ∈ Z & p > q;

— упорядоченным расслоением, если

∀ L

∈ R ∀ u ∈ L

, v ∈ L

: (u,v) ∈ Z => p < q.

Для орграфа на рис. 2.1.2 расслоениями с горизонтальными связя-

ми являются, например, {{1,3},{2}}, {{1,2},{3}}, с обратными связями —

расслоения {{3},{1},{2}}, {{2},{1},{3}}, упорядоченными — расслоения

{{1},{2,3}}, {{1},{2},{3}}.

В упорядоченном расслоении вершины любого слоя могут иметь пред-

ков только в слоях со строго меньшими номерами, а потомков — только

в слоях со строго большими номерами. В частности, вершины первого

слоя L

не имеют предков, а последнего слоя L

— потомков.

Упорядоченность расслоения S означает, что иерархические отноше-

ния, задаваемые организационной структурой D, полностью согласу-

ются с иерархическими отношениями, определяемыми той социальной

стратификацией по критерию М (различиям в имущественном, профес-

сиональном, политическом положении), которая порождает расслоение

организации S. Иначе говоря, начальник всегда принадлежит к более вы-

сокому социальному слою (по шкале стратификационных распределений

56 Иерархическое управление устойчивым развитием

М), чем его подчиненный. Однако неупорядоченные расслоения также

вполне способны отражать реально существующие ситуации. В частно-

сти, они могут использоваться для описания горизонтальных и обратных

(неформальных) связей в организационной структуре.

Предложенная математическая модель позволяет достаточно полно

отобразить такую специфическую черту социальных организаций, как

наличие формальной и неформальной (внеформальной и социально-

психологической) организации (Пригожин 1980). Формальная структура

описывается основным бесконтурным орграфом (или, что то же самое,

отношением строгой иерархии на множестве вершин — элементов орга-

низации), задающим отношения субординации. Неформальные связи

могут задаваться дополнительными орграфами, каждый из которых со-

ответствует определенной сети неформальных отношений. По сути дела,

такая трактовка означает переход к концепции динамических орграфов

(Угольницкий 1996).

Еще большие возможности для моделирования неформальных струк-

тур дает понятие расслоения орграфа. Расслоения могут использоваться

для описания социально-психологических групп, а также макрогрупп,

порождаемых социальной стратификацией. При этом порядок слоев ус-

танавливает относительную значимость групп в организационной струк-

туре.

Поскольку любая организационная структура может быть описана

бесконтурным орграфом, в моделировании и социальной верификации

иерархических организаций важно учитывать универсальные свойства

подобных систем.

Теорема 2.1.1 (Кофман, Дебазей 1968). Для любого бесконтурного орг-

рафа D существует упорядоченное расслоение.

Доказательство. Найдем все вершины D, не имеющие предков, и по-

местим их в слой L

. Затем вычеркнем все вершины из L

и их выходные

дуги (т. е. дуги, начальная вершина которых принадлежит L

); на полу-

ченном в результате вычеркивания орграфе вновь найдем вершины без

предков и поместим их в слой L

, и т. д. Очевидно, указанная процедура

приводит к упорядоченному расслоению, которое мы назовем прямым

и обозначим S

. По построению прямое расслоение D определяется од-

нозначно.

Можно доказать теорему 2.1.1 и в «обратном» порядке: найдем все вер-

шины в D, не имеющие потомков, и поместим их в слой L

. Затем вычерк-

нем все вершины из L

и их входные дуги (т. е. дуги, конечная вершина

которых принадлежит L

); на полученном в результате вычеркивания

орграфе вновь найдем вершины без потомков и поместим их в слой L

m–1

и т. д. Указанная процедура также приводит к упорядоченному расслое-

Глава 2. Методы и модели иерархического управления 57

нию, которое мы назовем обратным и обозначим S

. Обратное расслое-

ние также единственно.

Заметим, что прямое и обратное расслоения могут и не порождаться

никакой социальной стратификацией М; они определяются внутренними

организационными свойствами D. Прямое и обратное расслоения бес-

контурного орграфа не обязательно совпадают (рис. 2.1.3). Кроме того,

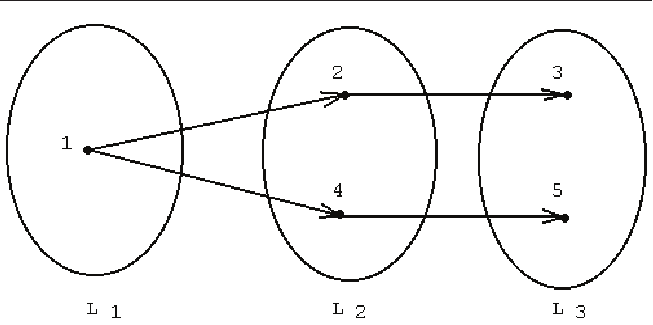
упорядоченное расслоение D может не быть ни прямым, ни обратным

(рис. 2.1.4). В прямом расслоении организации в слой L

попадают ее

члены, не имеющие начальников в данной организации (ее высшее ру-

ководство, в большинстве случаев — единственный руководитель орга-

низации); в слой L

— члены организации, имеющие начальников только

в слое L

; в слой L

— имеющие начальников только в слоях L

и L

и т. д.

до слоя L

, члены которого могут иметь начальников в любом предшест-

вующем слое и сами не имеют подчиненных в данной организации. Легко

провести аналогичные рассуждения и для обратного расслоения.

Теорема 2.1.2. (Угольницкий 2000). Число слоев в прямом и обратном

расслоениях бесконтурного орграфа D одинаково и равно длине макси-

мального пути в D плюс единица.

Расслоение S

назовем каноническим, если S

= S

. Пример кано-

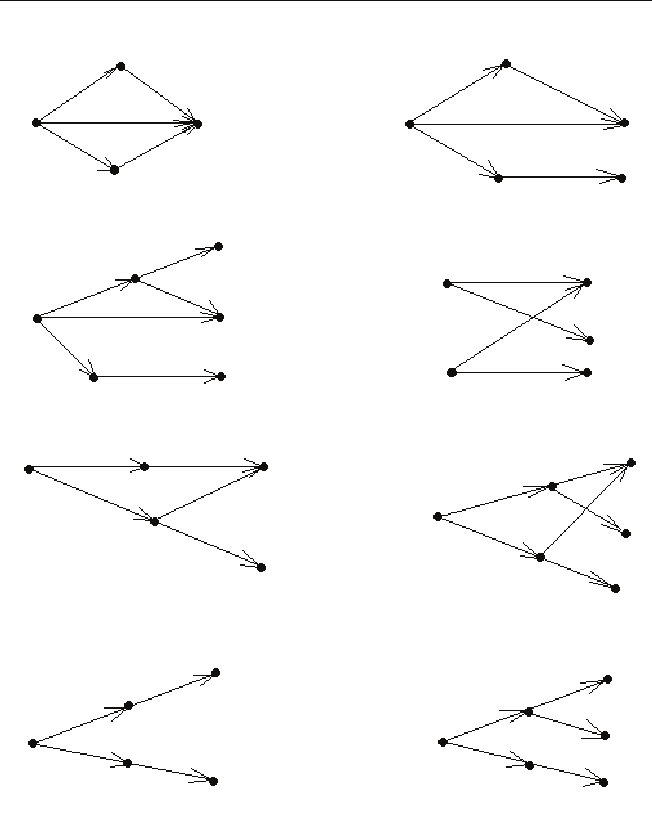
нического расслоения показан на рис. 2.1.5.

Если вершина u принадлежит одному из путей максимальной дли-

ны в бесконтурном орграфе, то назовем ее закрепленной, иначе назовем

ее свободной. Степенью свободы FP(u) вершины u в бесконтурном оргра-

фе D назовем разность между длиной максимального пути в D и длиной

Рис. 2.1.3. Расслоения орграфа: а — прямое; б — обратное

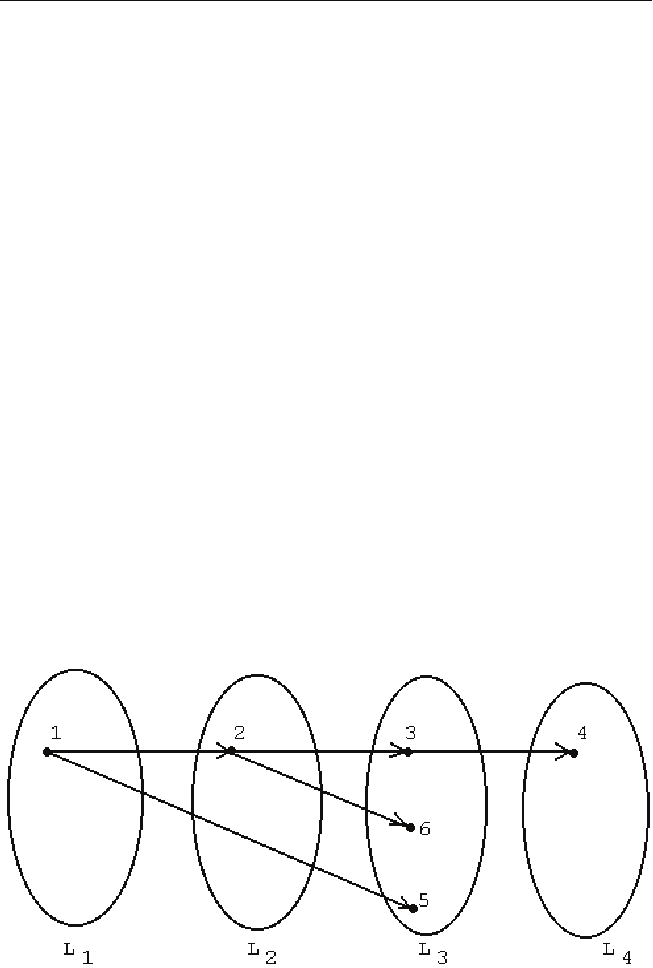
58 Иерархическое управление устойчивым развитием

максимального из тех путей от начальной вершины без предков к конеч-

ной без потомков, к которым принадлежит u (обозначим его W

max

). Оче-

видно, FP(u) = 0  u закрепленная. В общем случае 0 ≤ FP(u) ≤ c – 2, где

с — число слоев в прямом расслоении D. Орграф С, образованный всеми

закрепленными вершинами и соединяющими их дугами в бесконтурном

орграфе D, назовем каноническим подорграфом D. Орграф D назовем кано-

ническим, если он совпадает со своим каноническим подорграфом.

Теорема 2.1.3 (Угольницкий 2000). Бесконтурный орграф D является

каноническим тогда и только тогда, когда в D существует каноническое

расслоение.

На рис. 2.1.5 показан пример канонического орграфа, на рис. 2.1.4 —

неканонического. Прямое и обратное расслоения не являются единствен-

но возможными упорядоченными расслоениями бесконтурного орграфа

(в т. ч. и канонического). В частности, если некоторый слой содержит

более одной вершины, то любые два подмножества его вершин можно

рассматривать как два отдельных слоя (для канонического орграфа это

единственная возможность получить упорядоченное расслоение, отлич-

ное от канонического).

Упорядоченное расслоение назовем максимальным, если никакие два

слоя нельзя объединить, не нарушив упорядоченности. Прямое и обрат-

ное расслоения по построению являются максимальными. Обратное ут-

верждение неверно: на рис. 2.1.4 показан пример максимального расслое-

ния орграфа, которое не является ни прямым, ни обратным.

Канонический бесконтурный орграф назовем левым однополюсным,

правым однополюсным, двухполюсным, если в его каноническом рас-

слоении соответственно n

= 1, n

= n

= 1. Левый (правый)

Рис. 2.1.4. Упорядоченное расслоение, не являющееся ни прямым, ни обратным

Глава 2. Методы и модели иерархического управления 59

однополюсный орграф назовем: древовидным, если в его каноническом

расслоении n

≤ n

≤ ... ≤ n

≥ n

≥ ... ≥ n

cоответственно); строго

древовидным, если знаки неравенств строгие. Строго древовидные оргра-

фы соответствуют традиционным иерархическим пирамидам; при этом

левые орграфы удобно использовать для представления действий управ-

ляющего органа (руководителя организации) по передаче информацион-

ных воздействий и вещественно-энергетических ресурсов подчиненным,

а правые — для отображения информационных и вещественно-энерге-

тических потоков от подчиненных элементов к управляющему органу.

Канонический бесконтурный орграф назовем последовательным, если

в его каноническом расслоении дуги проводятся только между смеж-

ными слоями:

∀L

∈ S ∀u ∈ L

, v ∈ L

: (u,v) ∈ Z => q = p+1.

В этом случае все пути от L

до L

имеют одинаковую длину m – 1, а от-

ношения «начальник-подчиненный» возможны только между элемента-

ми смежных слоев. Бесконтурный орграф назовем левым (правым) одно-

значным, если каждая вершина имеет не более одной входной (выходной)

дуги. В левых однозначных организационных структурах каждый элемент

имеет единственного начальника, а в правых однозначных — единствен-

ного подчиненного. На рис. 2.1.6 показаны примеры канонических орг-

рафов различных классов.

В теориях социальной структуры принято считать, что любой инди-

вид в обществе входит в состав различных организаций и обладает в них

определенным рангом в соответствии со своим положением в иерархии.

В математической социологии, в свою очередь, разработаны подходы

Рис. 2.1.5. Каноническое расслоение орграфа

60 Иерархическое управление устойчивым развитием

Рис. 2.1.6. Примеры строго иерархических орграфов: 1 — левый однополюсный

орграф; 2 — левый древовидный орграф; 3 — левый строго древовидный орграф;

4 — последовательный орграф; 5 — левый древовидный последовательный орг-

раф; 6 — левый строго древовидный последовательный орграф; 7 — левый одно-

значный последовательный орграф; 8 — левый однозначный строго древовидный

последовательный орграф

7 8