Угльницкий Г.А. Иерархическое управление устойчивым развитием

Подождите немного. Документ загружается.

Глава 1. Концепция рациональности в общественных науках 41

вок профиля. Кемени и Снеллу удалось предложить категоричный набор

аксиом для функции расстояния между ранжировками d: P(A) x P(A) → R.

Далее, назовем медианой профиля ранжировок P

,..., P

такую ранжи-

ровку Р, для которой сумма d(P,P

) + ... + d(P,P

) минимальна, а средней

ранжировкой — такую ранжировку Р, что d

(P,P

) + ... + d

(P,P

) мини-

мальна. Целесообразно выбирать в качестве групповой ранжировки для

данного профиля медиану или среднюю ранжировку. Идея предлагаемого

подхода вполне понятна и разумна, но ее применение для определенных

профилей, как всегда бывает в теории выбора, приводит к трудностям

и парадоксам (Робертс, 1986).

В основу следующей модели, построенной и исследованной индий-

ским ученым А.Сеном, положена гипотеза о том, что для анализа пред-

почтений между парами альтернатив следует учитывать мнение только тех

субъектов, которых эти альтернативы непосредственно касаются.

Пусть имеется конечное множество субъектов N = {1,...,n}, n > 1, и ко-

нечное множество альтернатив A = {a,b,...,m}, m > 2. Индивидуальные

и групповые предпочтения являются линейными порядками на множе-

стве альтернатив, т. е. удовлетворяют условиям:

– связности: для любых а,b либо аP

b, либо bP

а;

– транзитивности: если аP

b и bP

c, то аP

– ацикличности: не может быть аP

b, bP

c, ..., кP

s, sP

a для любого s.

Обозначим С(a,b) = {i ∈ N: аP

b} — множество субъектов, для которых

а лучше b. Тогда субъект i называется решающим относительно а и b, если

из С(a,b) = {i} следует, что аPb. Справедлива

Теорема о паретовском либерале (парадокс Сена) (Алескеров и др.,

2006).

Пусть выполняются следующие условия:

— индивидуальные и групповое предпочтения являются линейными

порядками;

— правило группового выбора удовлетворяет условию единогласия;

— существуют альтернативы a,b,c,d и субъекты i,j такие, что i являет-

ся решающим для пар (a,b) и (b,а), а j — для пар (c,d) и (d,с).

Тогда функция группового выбора, удовлетворяющая перечисленным

условиям, не существует.

Рассмотрим задачу группового выбора в упрощенной постановке.

Пусть по-прежнему А — множество альтернатив, P

— предпочтения уча-

стников, описываемые линейными порядками, но функция группового

выбора имеет вид f : GPS(A) → А, т. е. группа выбирает только самую пред-

почтительную альтернативу (победителя).

Правило группового выбора f называется защищенным от манипу-

лирования, если ни один из субъектов ни в одном профиле не может

42 Иерархическое управление устойчивым развитием

изменить свои предпочтения так, чтобы в результате оказалась выбранной

наилучшая с его точки зрения альтернатива. Предположим, что f является

«отображением на», т. е. для любой a∈A существует профиль GP∈GPS(A)

такой, что f(GP) = a. Это условие не слишком ограничительно, в частно-

сти, оно слабее условия единогласия. Тем не менее, справедлив еще один

замечательный парадоксальный результат: любое недиктаторское прави-

ло группового выбора не защищено от манипулирования.

Теорема Гиббарда-Саттертуэйта (Мулен, 1991).

Пусть число альтернатив не меньше трех, а функция группового вы-

бора является «отображением на». Правило группового выбора защище-

но от манипулирования тогда и только тогда, когда оно является дикта-

торским.

Интересные исторические примеры манипулирования приведены

в (Алескеров и др., 2006).

Глава 2. МЕТОДЫ И МОДЕЛИ

ИЕРАРХИЧЕСКОГО УПРАВЛЕНИЯ

Неравенство между людьми (социальная иерархия) является фунда-

ментальной характеристикой общества. Важным выражением неравен-

ства служит социальная стратификация — разделение членов общества

на иерархически упорядоченные слои по определенному признаку или

их совокупности. В первом параграфе главы описаны модели социальной

иерархии и стратификации, особое внимание уделено моделям измерения

иерархического ранга сотрудников организации с учетом ее расслоения

по различным стратификационным признакам.

Иерархическая структура сложных систем с участием людей поро-

ждает необходимость специфических методов иерархического управ-

ления. Анализ этих методов основывается на изучении социальных

отношений и форм власти. Во втором параграфе главы на основе

проведенного анализа выделены три группы методов иерархическо-

го управления. В случае принуждения субъект верхнего уровня ставит

субъекта нижнего уровня в такие условия, в которых последний выну-

жден применять желаемую для первого стратегию. Такое воздействие

носит насильственный характер и осуществляется на административ-

но-законодательной основе. Интересы субъекта нижнего уровня при

этом совершенно не учитываются, т. е. отношения между субъектами

имеют субъектно-объектную природу. Если описать отношения между

субъектами как иерархическую игру Ведущего и Ведомого, то принуж-

дение означает воздействие Ведущего на множество допустимых стра-

тегий Ведомого.

В случае побуждения Ведущий создает условия, в которых Ведомому

более выгодно применять желаемую для Ведущего стратегию, нежели не

делать этого. Этот метод имеет природу экономического стимулирова-

ния и обычно реализуется посредством механизма штрафов и поощре-

ний с обратной связью. Здесь частично учитываются интересы Ведомого.

При теоретико-игровом моделировании побуждение означает воздейст-

вие Ведущего на функцию выигрыша Ведомого.

В случае убеждения Ведомый добровольно и осознанно разделяет

позицию Ведущего и придерживается желаемой для Ведущего страте-

гии (которая становится желаемой и для самого Ведомого). Этот метод

имеет социально-психологическую природу и придает отношениям Ве-

дущего и Ведомого субъектно-субъектный характер. В иерархической

44 Иерархическое управление устойчивым развитием

теоретико-игровой модели убеждение означает переход Ведущего и Ве-

домого к кооперации и совместную максимизацию ими суммарной функ-

ции выигрыша возникшей коалиции.

2.1. МОДЕЛИ СОЦИАЛЬНОЙ ИЕРАРХИИ

Неравенство между людьми — одна из фундаментальных характери-

стик общества. Люди различаются между собой по своим физическим,

психологическим, интеллектуальным, экономическим и другим харак-

теристикам; при этом, чем более развито общество, тем сильнее диффе-

ренциация его членов. Рассматривая каждый отдельный признак нера-

венства, можно разбить общество на слои, помещая в каждый слой всех

индивидов с одинаковыми или близкими значениями признака.

Это элементарное рассуждение сразу вызывает несколько далеко не

простых вопросов. Вопрос первый: какие признаки неравенства следует

учитывать? Будем рассматривать только те признаки, которые сущест-

венны для данного общества в данный период времени. Используем для

нумерации этих признаков индекс i, принимающий значения 1,2,...,М;

тем самым мы вводим в рассмотрение М признаков неравенства между

членами общества.

Вопрос второй: какое множество значений может принимать каж-

дый признак неравенства i = 1,2,...,M и как разделить это множество на

слои? Здесь могут встретиться различные ситуации. В некоторых случа-

ях множество значений признака конечно, дискретно, легко обозримо

и допускает естественное определение слоев. Например, при делении по

половому признаку имеются два значения, и человечество естественным

образом разделяется на два слоя (если не обсуждать волнующие пробле-

мы андрогинии и трансвестии). Более или менее понятно обстоит дело

с делением по этническим или, скажем, профессиональным признакам,

хотя составление списка профессий или национальностей представляет

собой нелегкую задачу. А вот описание, например, экономического не-

равенства уже приводит к непрерывному множеству значений признака,

т. е. величины состояния или годового дохода индивида. Для выделения

слоев здесь требуется определенное соглашение, примером которого

может служить шкала налогообложения: граждане с доходами от 0 до х

рублей в год должны отдавать государству у

процентов от величины до-

хода, граждане с доходом от х

+ 1 до х

— уже у

процентов (конечно, у

> у

), и т. д. до самых богатых, отчисляющих у

процентов. Тем самым

сформирована экономическая стратификация (с точки зрения налого-

вой службы), делящая всех граждан на р слоев. Наиболее общим и удоб-

ным для теоретического рассмотрения является предположение о том,

Глава 2. Методы и модели иерархического управления 45

что признак неравенства может принимать любое действительное зна-

чение. В простых ситуациях можно ограничиться дискретными значе-

ниями признаков.

Вопрос третий: являются ли выделенные слои равноправными или

они некоторым образом ранжированы? Сам смысл базового понятия не-

равенства заставляет принять вторую точку зрения, что приводит к кон-

цепции социальной стратификации. Согласно П. Сорокину (1992, 1993),

стратификация — это разделение совокупности людей на классы в ие-

рархическом ранге, что выражается в существовании высших и низших

слоев. Социальная стратификация означает не просто различное поло-

жение в обществе индивидов или целых слоев, но именно неравное их

положение (Рывкина, 1989). «Стратификация — это процесс, в резуль-

тате которого семьи и индивиды оказываются не равными друг другу

и группируются в иерархически расположенные страты с различным

престижем, собственностью и властью» (Dictionary, 1964). Более сложное

определение включает и объективные, и субъективные факторы форми-

рования социальной структуры общества: «Суть стратификации — не-

одинаковость положений и их оценки» (Davis, 1942).

Подчеркнем, что упорядоченность стратификации, как и выделение

существенных признаков неравенства или разбиение множества их значе-

ний на слои, всегда определяется для конкретного общества на конкрет-

ном промежутке времени. В матриархальных обществах при разделении

по половому признаку лидировали женщины; затем пальма первенства

перешла к мужчинам, которые благополучно удерживают ее и в современ-

ном обществе, несмотря на отчаянные попытки феминисток и борцов за

политкорректность. Титульная нация в многонациональном государст-

ве располагает множеством преимуществ, которые моментально превра-

щаются в недостатки при переезде представителя этой нации в соседнее

государство. Экономическая стратификация кажется совершенно есте-

ственной, но не следует забывать о судьбе «буржуев» в обществах побе-

дившего пролетариата.

Обозначим через Х множество индивидов, составляющих общество.

Назовем стратификацией по i-му признаку S

упорядоченное разбиение

множества Х на подмножества (слои) L

, L

,..., L

такое, что любые два

слоя разбиения не пересекаются, а объединение всех слоев дает множе-

ство Х (m

— число слоев в разбиении S

, i = 1,2,...,M, где М — общее чис-

ло признаков социальной стратификации). Упорядоченность разбиения

означает, что нумерация слоев в нем определяется однозначно. Номер

слоя, к которому принадлежит индивид х из множества Х в стратифика-

ции S

, естественно назвать его социальным рангом по признаку i. Набор

46 Иерархическое управление устойчивым развитием

рангов по всем стратификационным признакам определяет социальную

позицию соответствующего индивида.

Обратимся к упомянутой выше теоретической модели, предполагая,

что стратификационные признаки могут принимать любые действитель-

ные значения; тогда социальная позиция индивида х становится точкой

обычного числового пространства R

, размерность которого равна числу

стратификационных признаков:

х = (х

, х

, ..., х

) ∈ R

, (2.1.1)

где x

— социальный ранг индивида по признаку i, i=1,...,M. В такой мо-

дели стратификация S

представляет собой упорядоченное разбиение чи-

словой оси:

= (–∞, x

] ∪ (x

, x

] ∪ ... ∪ (x

, ∞). (2.1.2)

Тогда стратификационный слой естественно считать интервальной

величиной, т. е. называть стратификационным слоем по признаку i ин-

тервал из формулы (2.1.2).

Таким образом, мы пришли к концепции социального пространства,

допускающей двоякую трактовку. С одной стороны, можно непосред-

ственно задать социальную стратификацию как разбиение множества

индивидов на слои по некоторому признаку; номер слоя служит соци-

альным рангом индивида в смысле соответствующего признака, набор

рангов образует социальную позицию индивида, а набор всех социаль-

ных позиций составляет множество, которое естественно назвать дис-

кретным социальным пространством. С другой стороны, можно исходить

из наличия многомерного числового пространства, оси которого отвеча-

ют стратификационным признакам; тогда социальная позиция индивида

определяется как точка (вектор) многомерного числового пространства,

называемого непрерывным социальным пространством. Компоненты со-

циальной позиции (проекции вектора на стратификационные оси) суть

социальные ранги. Разбиение (2.1.2) задает набор социальных слоев по

признаку i следующим образом: все социальные позиции, i-я компонен-

та которых (социальный ранг) попадает в интервал (x

j–1

, x

], принадлежат

социальному слою L

по признаку i.

В теоретико-методологическом отношении интересно, что «упорядо-

ченность стратификации» в любых аналитических (например, структур-

но-функционалистских) моделях чревата субъективизмом выбора стра-

тификационных параметров и их ранжирования самим исследователем,

в то время как в синтетических (например, в «социократической» теории

П. Бурдье) любой вектор пространства упорядочивает позиции по уни-

Глава 2. Методы и модели иерархического управления 47

версальному критерию распределения власти, но в данном конкретном

«поле», поэтому формально они более «объективны» и по способу ранжи-

рования — не дискретны. Согласно П. Бурдье, «позиция данного агента

в социальном пространстве может определяться по его позициям в раз-

личных полях, т. е. в распределении власти, активированной в каждом

отдельном поле. Это, главным образом, экономический капитал в его

разных видах, культурный капитал и социальный капитал, а также сим-

волический капитал, обычно называемый престижем, репутацией, име-

нем и т. п.» (Бурдье 1993:57).

Приняв изложенную концепцию социального пространства, мы пол-

ностью отождествляем в рамках модели реального индивида во всем его

многообразии с его модельным образом — социальной позицией. Без-

условно, тем самым исходный объект сильно обедняется, но зато появ-

ляется хорошо структурированный и даже операционализированный

предмет — индивид в аспекте социального неравенства. Производится

абстрагирование, после которого с абстрактной моделью можно опери-

ровать по формальным правилам, а полученные результаты интерпрети-

ровать в исходных содержательных терминах.

Отметим, что построенная модель социального пространства позво-

ляет в определенном смысле снять вопрос о том, что первично: общест-

во или индивид. Можно исходить из индивида (точки) и определять про-

странство (общество) как совокупность всех возможных точек, а можно

признавать наличие пространства (общества) и рассматривать различные

точки (индивидов), существующие в этом пространстве: получаемые при

этом результаты будут инвариантными.

Модель непрерывного социального пространства отвечает интуиции

П. Бурдье: «прежде всего социология представляет собой социальную то-

пологию. Так, можно изобразить социальный мир в форме многомерного

пространства, построенного по принципам дифференциации и распреде-

ления, сформированным совокупностью действующих свойств в рассмат-

риваемом социальном универсуме, т. е. свойств, способных придавать их

владельцу силу и власть в этом универсуме. Агенты и группы агентов оп-

ределяются, таким образом, по их относительным позициям в этом про-

странстве. Каждый из них размещен в позиции и в определенные клас-

сы близких друг к другу позиций (т. е. в определенной области данного

пространства), и нельзя реально занимать две противоположные области

в пространстве...» (Бурдье 1993:55–56).

Дадим более детальную характеристику областей дискретного соци-

ального пространства, опираясь на аналитическую трактовку понятия

социальной группы. Следуя П. Сорокину (1993), определим в качестве

48 Иерархическое управление устойчивым развитием

элементарной группы реальную совокупность лиц, объединенных во

взаимодействующее целое каким-либо одним признаком, достаточно

ясным и определенным, не сводимым к другим признакам; под куму-

лятивной (составной) социальной группой будем понимать совокуп-

ность субъектов, связанных во взаимодействующее целое не одним,

а несколькими сходными элементарными признаками. Этот подход ве-

дет к следующим естественным определениям в дискретном социаль-

ном пространстве.

Элементарная социальная группа по i-му признаку — это множество

социальных позиций, имеющих одинаковый социальный ранг j по это-

му признаку:

G(i

) = {x ∈ X: x

= j}. (2.1.3)

Составная социальная группа по признакам i

,..., i

— это множество

социальных позиций, имеющих одинаковые социальные ранги j

,..., j

по указанным признакам:

C(i

,..., i

) = {x ∈ X: x

= j

,...,x

= j

}. (2.1.4)

Из определения (2.1.4) следует, что полностью однородная социальная

группа, т. е. C(i

,..., i

), представляет собой единственную социальную

позицию (j

,..., j

). Таким образом, множество индивидов, неразличимых

по всем стратификационным признакам, отображается точкой (конечно,

в смысле интервального определения) в модели дискретного социального

пространства. Элементарная социальная группа также является частным

случаем составной группы, т. к. формула (2.1.3) получается из (2.1.4) при

k = 1. Дадим еще несколько определений для дискретного социального

пространства.

Элита по признакам i

,..., i

— это множество социальных позиций,

имеющих наивысшие ранги по всем указанным признакам:

E(i

,..., i

) = {x ∈ X: x

= m

,..., x

= m

}. (2.1.5)

Соответственно, люмпены по признакам i

,..., i

— это множество соци-

альных позиций, имеющих самые низкие ранги по этим признакам:

L(i

,..., i

) = {x ∈ X: x

= ... = x

= 1}. (2.1.6)

Конечно, в большинстве случаев в качестве признаков i

,...,i

следует

выбирать наиболее существенные: например, Ч.Р. Миллс при выделении

американской элиты использует три признака стратификации: экономи-

ческий, политический и военный (Миллс 1959). Часто при определении

элиты и люмпенов считается, что {i

,..., i

} = M, т. е. учитываются все стра-

тификационные признаки; определения (2.1.5)–(2.1.6) дают более тон-

Глава 2. Методы и модели иерархического управления 49

кую характеристику. Известное понятие статусной несовместимости (см.,

например, (Комаров 1992)) в его крайнем выражении можно формали-

зовать следующим образом: статусная несовместимость имеет место для

социальной позиции х ∈ Х, если найдутся такие признаки i,j = 1,2,...,M,

что x

= 1, x

= m

. Характерный пример — низкая оплата труда высоко-

квалифицированного специалиста.

П.Сорокин (1993) определяет класс как совокупность лиц, сходных по

профессии, имущественному положению, объему прав, а следователь-

но, имеющих тождественные профессиональные, имущественные и со-

циально-правовые интересы. Тогда в модели дискретного социального

пространства класс становится частным случаем составной социальной

группы (2.1.4), когда i

— профессиональный признак стратификации,

— имущественный, i

— социально-правовой. В этом случае «высший»

класс совпадает с элитой, а «низший» — с люмпенами по соответствую-

щим признакам. Фактически социальное пространство Сорокина полно-

стью определяется указанными тремя признаками. Этот факт использовал

в своей модели В.Анурин, который предложил геометрическое представ-

ление социального пространства (Анурин 1993) и провел его частичную

эмпирическую апробацию (Анурин 1995).

Элементарной социальной группой по признаку i в модели непрерывного

социального пространства назовем множество социальных позиций

) = {x ∈ X: x

< x

j+1

}, (2.1.7)

социальный ранг которых по i-му признаку равен j; таким образом, чис-

ло возможных элементарных социальных групп по каждому стратифи-

кационному признаку равно числу слоев в соответствующей стратифи-

кации.

Составной социальной группой по признакам i

,..., i

в непрерывном со-

циальном пространстве назовем множество социальных позиций

C(x

,..., x

) = {x ∈ X: x

< x

j+1

,...,

< x

p+1

}. (2.1.8)

Обратим внимание на то, что социальные группы определены как от-

крытые множества. Это означает, что социальные позиции, лежащие на

границе областей, определенных неравенствами (2.1.7) и (2.1.8), не при-

надлежат соответствующим социальным группам. Здесь оправдана эти-

мологическая подсказка: указанные граничные (marginal) позиции явля-

ются маргинальными. Маргинальные социальные позиции, лежащие на

границе группы, очень близки к ней, но не входят в ее состав.

Рассмотрим теперь специфические области социального простран-

ства. Согласно П. Бурдье, «распределения в физическом пространстве

50 Иерархическое управление устойчивым развитием

благ и услуг, соответствующих различным полям ... стремятся наложить-

ся друг на друга, по меньшей мере приблизительно; следствием этого

является концентрация наиболее дефицитных благ и их собственников

в определенных местах физического пространства (Пятая авеню, улица

Фобур де Сент-Оноре), противостоящих во всех отношениях местам, объ-

единяющим в основном, а иногда — исключительно, самых обездолен-

ных (гетто)» ... «Эти места ... не могут быть поняты иначе, ... как в связи

с коммерческими предприятиями, принадлежащими тому же полю, но

занимающими другие области парижского пространства... В той мере,

в какой оно лишь концентрирует позитивные полюса из всех полей (так

же, как гетто концентрирует все негативные полюса), это пространство

не содержит истину в себе самом» (Бурдье 1993:41–42).

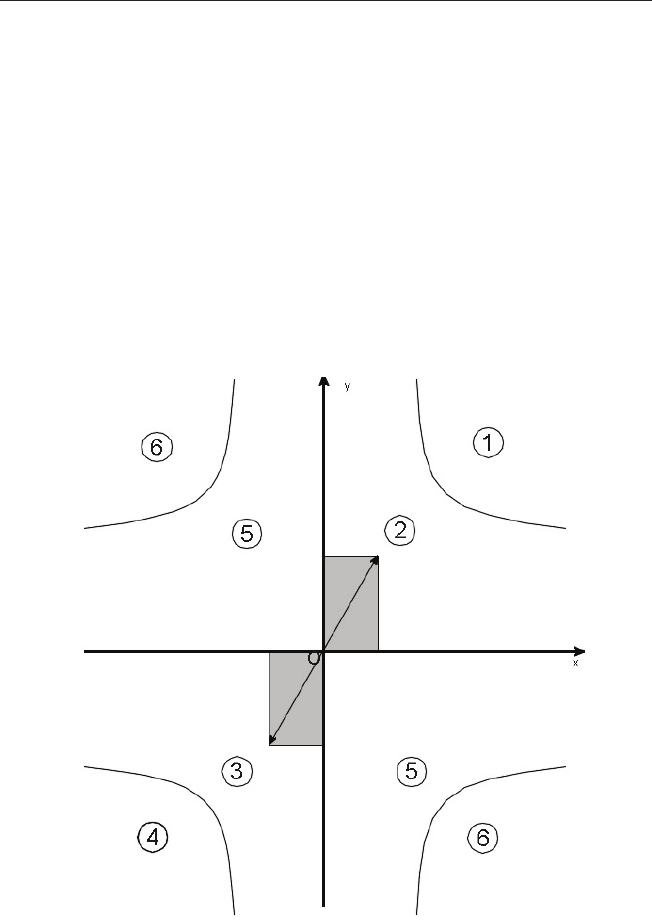
Схема на рис. 2.1.1 проясняет социологический смысл квадрантов со-

циальной плоскости (в общем случае — ортантов социального простран-

Рис. 2.1.1. Области социального пространства

1 — элита; 2 — средний класс; 3 — низшие классы; 4 — гетто; 5 — область умерен-

ной статусной несовместимости; 6 — область сильной статусной несовместимости