Tsebelis G. Veto Players: How Political Institutions Work

Подождите немного. Документ загружается.

CHAPTER 2: COLLECTIVE VETO PLAYERS

On the basis of Chapter 1 we can analyse situations were the veto players are individuals

(like the US president), or have monolithic majorities (like a communist party), or are deciding

by unanimity (like the Polish parliament in the early 18

century). However such situations are

rare. Most often decisionmaking involves participation of some collective veto player like a

committee, a party, or a parliament. Rare are the cases where such actors are monolithic, or even

have a homogenous majority inside them. And today cases that involve unanimous

decisionmaking are exceptional. Therefore we need to generalize and see whether the intuitions

generated by Chapter 1 hold in more familiar configurations of preferences and modes of

decisionmaking.

While this chapter is essential for moving away from simplifications and increasing the

correspondence between theoretical concepts and political reality it is significantly more

technically demanding than the previous one. In addition, while the conclusions presented in

Chapter 1 were intuitive to the point that they may have seemed obvious to readers, some of the

ideas here are counterintuitive. This chapter reaches the conclusion that the analysis of Chapter 1

provides a very good approximation to political phenomena, but the argument is more

challenging to follow.

The non-technical reader may be tempted to skip a chapter that is significantly more

difficult than the previous one, has counterintuitive results, only to reach the same conclusions. I

will try to dissuade the reader from adopting this strategy through the use of a long introduction,

which will explain the problems generated by collective veto players. I hope that this

introduction will generate sufficient interest to the conceptual problems that readers will go

through the whole chapter. Plan B (in case my strategy fails), uses long conclusions that

summarize the most important ideas presented in this chapter. So readers are presented with two

options. A non-technical reader may read the introduction and the conclusions of this chapter and

then move on to the rest of the book without being surprised by the arguments made later and

may come back to the rest of Chapter 2 at another time. The reader who wants to apply veto

player theory to cases not covered in this book (countries I do not discuss here, or

decisionmaking at the state or local level) has to go through sections I, II, and III.

Transition from individual to collective veto players generates two problems. First, the

configuration of winset of the status quo may become complicated, that is, the outcomes of

decisionmaking become more complicated. We will need to approximate these outcomes in

some simple way. Second, collective veto players violate one important assumption we made

about individuals: under majority rule collective veto players cannot unambiguously choose

between a series of outcomes the one they prefer. In other words, the choices of collective veto

players are ambiguous. This is obviously more than a mere inconvenience, or a lack of

descriptive accuracy; it may make collective veto players unable to make a proposal and thus

undermine completely the analysis of the previous chapter. I will explain under what conditions

this problem can be eliminated, and argue that these conditions occur frequently. Let me focus

on each one of these points.

INSERT FIGURE 2.1

1. The outcomes of decisionmaking are more complicated. Consider the 7 individual veto

players (1,2,…7), and the status quo (SQ) presented in Figure 2.1. Which points can defeat the

status quo by a unanimous decision of the seven veto players?

The points that can defeat the status quo can be located if we consider the points that each

individual veto player prefers over the status quo. The reader is reminded that such points are

located inside circles that go through the status quo, and have center the preferences of each veto

player. The intersection of all these circles is the heavily shaded lens in Figure 2.1. Similarly, we

can identify all the points that cannot be defeated by a unanimous decision of the seven veto

players (the unanimity core). These points form the whole heptagon 1234567.

Indeed, any

point inside the heptagon cannot be replaced without one of the veto players objecting. The

hatched area in Figure 2.1 presents the unanimity core of this collective veto player.

What happens if this collective veto player uses less restrictive decisionmaking rules?

What if decisions are made by qualified majority of simple majority instead of unanimity? The

intuitions generated from Chapter 1 indicate that policy stability should decrease, that is, that

more points could defeat the status quo (the winset of the status quo should expand), and fewer

points should be invulnerable (the core should shrink). Let us consider one case of each rule.

First, a qualified majority decision by six out of the seven actors, and then, a simple majority (of

four out of seven members).

The points that can defeat SQ by a qualified majority of 6/7 (the 6/7 qualified majority

winset of SQ) can be identified if we consider the intersection of six out of the seven circles

around the points 1, 2, …,7 of Figure 2.1. I present this area shaded lighter than the points that

could defeat SQ under unanimity rule (the unanimity winset of SQ), and as the reader can verify

it includes this unanimity winset of SQ. In order to locate the points that cannot be defeated by a

6/7 majority (the 6/7 core), we consider all the possible combinations of 6 out of the 7 players,

and take the intersection of their unanimity cores.

In Figure 2.1 this intersection is represented

by the crosshatched area. The reader can verify that it is included in the unanimity core of the

I have selected them in way that none of them is included in the unanimity core of the others, otherwise the

unanimity core would have been a different polygon (with fewer sides).

A more expedient way would be to connect the seven players by ignoring one of them each time (connect 1 and 3,

2 and 4, 3, and 5 etc.) and consider the polygon generated by the intersection of these lines.

seven players.

What happens if the 7 players decide by majority rule? In order to calculate the set of

outcomes that defeat the status quo (the winset of SQ), we have to consider the intersections of

any four circles. The lightly shaded area in Figure 2.1 gives the area of the majority winset of

SQ, and this area includes the qualified majority winset (which includes the unanimity winset). If

we try to identify the core of majority decisionmaking we will see that this core is empty, that is,

there is no point that cannot be defeated by majority rule. As we will see below, the conditions

under which there is a point that cannot be defeated by any other point under majority rule are

very exceptional indeed.

Figure 2.1 demonstrates two important points. First, policy stability generated by

collective veto players follows the intuitions generated by Chapter 1: it decreases (that is, the

winset of SQ expands and the core shrinks) as the decisionmaking rule moves from unanimity to

qualified majority, to simple majority. Second, the calculations become more complicated every

time, that preferences of a collective veto player are not expressed by circles, and the winset of

collective veto players takes unusual shapes. This chapter aims at identifying a simple way of

approximating the outcomes of the decisionmaking process (the points that can defeat the status

quo) when a veto player is collective.

2. The choices of collective veto players are ambiguous. When an individual veto player

compares three possible positions of SQ we can assume that his preferences are transitive that is,

if he prefers SQ1 over SQ2, and SQ2 over SQ3, then, he will also prefer SQ1 over SQ3. This

transitivity of preferences enables the individual veto player to select unambiguously among any

set of alternatives, that is, to identify the alternative that he prefers the most.

However,

The individual may be indifferent between two alternatives. Indifference is different from ambiguity of

preferences as will become clear below. I ignore here cases of indifference for simplicity of exposition.

collective veto players deciding under majority rule do not have the same transitivity of

preferences. Figures 2.2 and 2.3 provide in two steps the intuition behind the argument.

INSERT FIGURE 2.2

In Figure 2.2 there are three individual decision makers and the status quo located in the

middle of the triangle 123. Let us first try to identify the points that defeat the status quo under

simple majority rule. Following the rules set in Chapter 1, I draw the indifference curves (circles)

of the three players and consider the intersections of any two of them. In the figure I have shaded

W(SQ), which has a flower-like shape. The edges of the shaded area are the points of

indifference of different majorities. In Figure 2.1 I represent the preferences of the coalition 1

and 3 with a different pattern, and I select a point SQ1 that defeats SQ because it is preferred by

these two decisionmakers. Note that I have selected SQ1 at the edge of the pedal. The only

reason for this choice is to minimize the subsequent drawing, but there is no loss of generality to

the argument I present.

INSERT FIGURE 2.3

Let us now move to a second step: identify the set of points that defeat SQ1. In Figure 2.3

I have drawn the one additional circle required for this operation, the circle around point 2 (the

other two circles already exist because of the selection of SQ1). The hatched area in Figure 2.2

are th points that defeat SQ1 by different majorities (winset of SQ1: (W(SQ1)).

I remind the reader that we started from SQ and identified the other two points as

follows: SQ1 was a point that defeats SQ by majority rule (decision-makers 1 and 3 prefer SQ1

over SQ). Similarly, SQ2 was a point that defeats SQ1 by majority rule (decision-makers 1 and 2

preferred SQ2 over SQ1). If the collectivity of 1, 2, and 3 were a single individual that preferred

SQ2 over SQ1 and SQ over SQ1, then by transitivity this individual would also prefer SQ2 over

SQ. However, this is not the case for our collectivity. It prefers SQ to SQ2. In other words, our

collectivity has ambiguous preferences generated by majority rule

SQ2 ? SQ1 ? SQ ? SQ2 (2.1)

where ? stands for “majority preferred.” Note that the three preferences are not generated

by the same majorities. 1 and 2 are responsible for the first choice, 1 and 3 for the second, and 2

and 3 for the third. This ambiguity of preferences, this “intransitivity” of majority rule as is

known in technical terms was known by Condorcet, but was explored and generalized

extensively by Arrow (1951)

and in a spatial context by McKelvey (1976 and 1978) and

Schofield (1977 and 1978).

For our purposes the best way to note the ambiguous pattern of preferences generated by

majority rule and described by (2.1) is to highlight the fact the collectivity cannot make up its

mind between SQ and SQ2: SQ defeats SQ2 by direct comparison but it is defeated by SQ2 in a

mediated or indirect comparison (if SQ1 is compared with both of them it eliminates SQ and is

eliminated by SQ2).

Why should we care about the ambiguity of collective preferences, that is the fact that SQ

directly beats SQ2, while it is indirectly defeated by SQ2? Because we do not know how SQ and

SQ2 will be compared. We do not know which one is first on the agenda. More to the point, if

the collectivity cannot make up its mind, strategic entrepreneurs will present a sequence of

choices that lead to one or the other outcome. In fact, McKelvey (1976 and 1978) and Schofield

(1977 and 1978) have shown that the problem is much more serious than my description presents

it: these “intransitivities” can cover the whole space, that is, an astute agenda setter can present a

society with a series of choices structured appropriately and lead it to any result he or she wishes.

In the above discussion I ignore indifference relations for reasons of simplicity of the exposition.

Arrow has, of course, shown the impossibility of any decisionmaking rule to conform to five plausible and

This analysis may completely undermine the arguments I made in Chapter 1. Collective

veto players cannot chose unambiguously by majority rule. This means that if a collective veto

player controls the agenda and makes an offer to another veto player a clear choice should not be

expected because collective veto players come to contradictory results when they have to

compare two points (let alone the infinity contained in the winset of the others).

In subsequent sections, I will demonstrate that these objections, which could have been

fatal for my arguments, are in fact mere inconveniences. The winset of a collective veto player

may not be a circle, but a circle that contains it can be identified and the analysis can be carried

out in an approximate way. Collective veto players may not be able to make choices in general,

but under empirically plausible conditions they can select a small area among all the available

alternatives. So, the analysis of Chapter 1 holds approximately for collective veto players too.

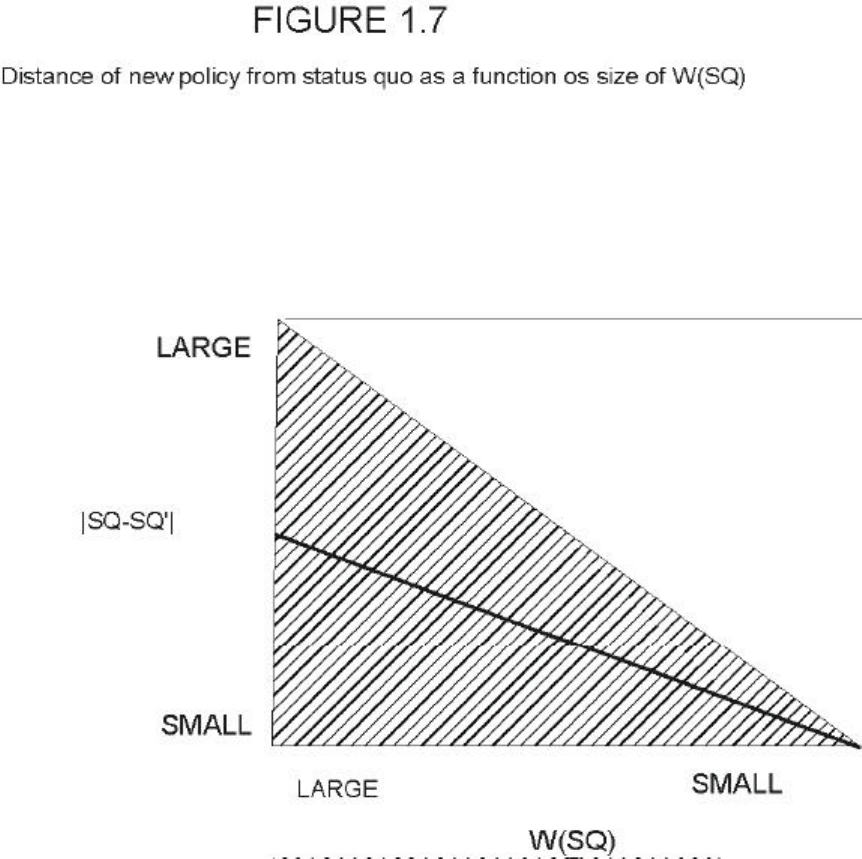
However, there is a price to be paid. These approximations, while on the average

accurate, are not always true. For example, as I demonstrated in the previous chapter, while the

set of points that defeat the status quo shrinks with the distance of two individual veto players

(along the same line according to lemma 2) with collective veto players it is possible to decrease

the distance and decrease the size of the status quo. This can happen under specific distributions

of the individual players and/or positions of the status quo. It is not a frequent phenomenon, but

it is possible. As a result, I cannot present as theorems the claims made in this chapter, because

positions of individual actors can be found to falsify such theorems. The claims will be presented

as “conjectures” and the arguments for the validity of these conjectures will be presented.

The chapter is organized to mirror Chapter 1 (discussion of winsets first, of sequence

afterwards). I have interpolated one section: to discuss collective veto players deciding by

qualified majority, that turns out to be quite different from simple majority. So, the overall

desirable requirements.