Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

331

диагональные м иноры матрицы Гурвица имеют вид

∆

= a

, ∆



, ∆



, . . .

. . . , ∆



0 0 . . . 0

. . . 0

. . . . . . . . . . . . . . . . . . . . . . .

0 0 0 0 0 0



Следовательно, критерий устойчивости Рауса — Гурвица сводится к сле-

дующему требованию:

∆

> 0 , ∆

> 0 , . . . , ∆

> 0 . (14.4)

Применим этот критерий к исследованию корней характеристическо-

го уравнения линейного осциллятора p

+ 2γp + ω

= 0. Условия (14.4)

сводятся к условию положительности коэффициентов γ > 0 и ω

> 0.

Для характеристического уравнения третьего порядка

+ ap

+ bp + c = 0 (14.5)

одной положительности коэффициентов для устойчивости равновесия уже

недостаточно. Действительно, записав определитель Гурвица, найдем глав-

ные миноры: ∆

= a, ∆

= ab − c, ∆

= c(ab − c). Все миноры будут

положительными, если ab > c. При невыполнении одного из указанных

условий (положительность коэффициентов, или ab > c) состояние равно-

весия неустойчиво. Характер возникающей неустойчивости существенно

зависит от параметров (см., например, таблицу 6.1 из книги [4]).

Число “устойчивых” (“неустойчивых”) корней определяет размерность

так называемого устойчивого W

(неустойчивого W

) многообразия, на

котором вблизи состояния равновесия расположены приближающиеся к

нему (уходящие от него) траектории. Когда эти многообразия двумерны,

мы видим на них привычные нам устойчивые (неустойчивые) узлы или

фокусы. Будут ли на этих многообразиях узлы или фокусы, зависит от

знака дискриминанта

∆(a, b, c) = −a

+ 4b

+ 4a

c − 18abc + 27c

При ∆ < 0 будут узлы; при ∆ > 0 — фокусы.

332

Критерий Рауса — Гурвица не всегда удобен для определения устой-

чивости. Так, для больших значений n приходится проделывать слишком

громоздкие вычисления определителей и, следовательно, трудно записать

условие устойчивости в общем виде. Кроме того, если система неустой-

чива, то трудно сказать, сколько имеется корней с положительной дей-

ствительной частью, т.е. каков порядок неустойчивости. Хорошо бы иметь

критерий, свободный от этих недостатков, который мог бы быть обобщен

на распределенные системы (левая часть характеристического уравнения

которых не полином, а к вазиполином, т. е. полином по exp[δp]. Для по-

строения такого критерия удобен метод D-разбиений. Он заключается в

следующем.

Пусть в характеристическое уравнение входит параметр λ, т. е. ∆(λ, p) =

= 0. Нам надо знать, как при изменении λ меняется порядок неустойчи-

вости, т. е. что происходит с корнями уравнения, как они передвигаются

по плоскости p. Если при изменении λ корни не попадают на мнимую

ось, то с точки зрения устойчивости вообще ничего не меняется; если же

хотя бы один корень попал на мнимую ось, то данное значение парамет-

ра λ будет критическим, так как дальнейшее малое изменение λ может

привести к изменению порядка неустойчивости на единицу. Нам надо

связать изменение параметра λ, с фактом пересечения корнями мнимой

оси. Так как корни характеристического уравнения комплексные, то удоб-

но считать и λ комплексной величиной. Пусть на комплексной плоскости

p корень пересекает мнимую ось, тогда на комплексной плоскости λ, это

соответствует переходу параметра через некую границу, разделяющую

области с различным порядком неустойчивости. Перебирая все значения

p, лежащие на мнимой оси, и сопоставляя им значения λ, мы построим в

плоскости λ границу D-разбиения, т.е. границу, разделяющую плоскость

параметров на области с разным порядком неустойчивости.

Для построения этой границы поставим в соответствие точкам пло с-

кости p точки плоскости λ, т.е. найдем из характеристического уравнения

связь λ = f(p). Если p меняется от −∞ до ∞, то и λ пробегает некую

кривую на плоскости λ, причем в определенном направлении. Если за-

штриховать правую сторону мнимой оси, то и на этой кривой, лежащей

на плоскости λ, следует заштриховать правую по направлению движе-

ния сторону. Тогда можно ут верждать, что переход из незаштрихованноп

области в заштрихованную увеличивает порядок неустойчивости на еди-

ницу. Переход с плоскости p на плоскость λ соответствует конформному

отображению. Для построения такого конформного отображения необхо-

димо, чтобы можно было разрешить уравнение ∆(λ, p) = 0 относительно

λ, и, кроме того, необходима непрерывность и дифференцируемость f (p),

333

)

=1l

)

D( )

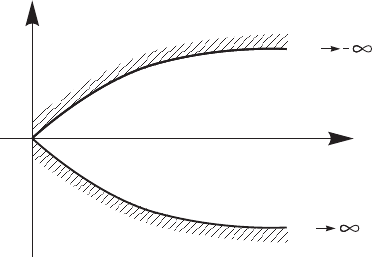
Рис. 14.1. Разбиение плоскости параметров λ на области с

разным порядком неустойчивости для уравнения p

+ p +

+ λ = 0

т.е. функция должна быть голоморфной.

Рассмотрим простейший пример: p

+ p + λ = 0. Разрешая это уравне-

ние относительно λ, найдем λ = −p

− p, откуда при p = iω находим

λ = ω

− iω. Следовательно, Re λ = ω

, a Im λ = −ω. Таким обра-

зом, Re λ = (Im λ)

. Граница области неустойчивости — это парабола

(рис. 14.1). Внутри нее — область устойчивости. Вне — порядок неустой-

чивости D(λ) = 1.

Метод D-разбиений можно использовать и в случае, когда число кор-

ней характеристического уравнения счетно. Именно таким, как мы видели

в гл. 10, оказывается спектр резонатора без излучения на границах. Если

резонатор одномерный, то спектр волновых чисел всегда эквидистантный:

k = πn/l (n = 1, 2, . . . ) для резонатора с идеальным отражением на кон-

цах и k = 2πn/l для кольцевого резонатора. Поскольку в дисперсионном

уравнении D(ω, k) = 0 k — теперь фактически номер моды k ∼ n, то из

этого уравнения, перебирая n, нетрудно определить границу устойчиво-

сти распределенной системы с дискретным спектром.

Приведем простой пример. Будем считать, что резонатор кольцевой и

рассмотрим его устойчивость только по отношению к волновым возмуще-

ниям, распространяющимся вправо. Если в среде нет дисперсии и потерь,

то из волнового уравнения u

+ v

= 0 сразу получаем значения частот

= 2πnv

/l. Все частоты действительны, так как все счетное множе-

ство корней характеристического уравнения D(p, n) = 0 лежит на мнимой

оси плоскости p = iω. Таким образом, система устойчива. Если в той же

среде учесть высокочастотные потери, например вязкость, то уравнение

бегущей волны примет вид u

−νu

= 0, а решения характеристи-

334

ческого уравнения запишутся в виде ω

= (2π/l)(v

+ iνn2π/l)n. Теперь

все корни лежат в верхней полуплоскости ω плоскости со (или в левой

полуплоскости плоскости p), т.е. устойчивость лишь усилилась и стала

экспоненциальной.

Введем в среду отрицательную диссипацию, проявляющуюся неза-

висимо от масштабов возмущения. Для определенности будем считать,

что такая неравновесная среда моделируется цепочкой, изображенной на

рис. 14.2,а. Уравнение бегущей волны в такой среде запишем в виде

∂u

∂t

+ v

∂u

∂x

− ν

∂

∂x

− γu = 0 . (14.6)

Отыскивая решения u(x, t) = v exp[i(ωt −kx)] для кольцевого резонатора,

получаем характеристическое уравнение:

2πnv

+ iν



2πn



−

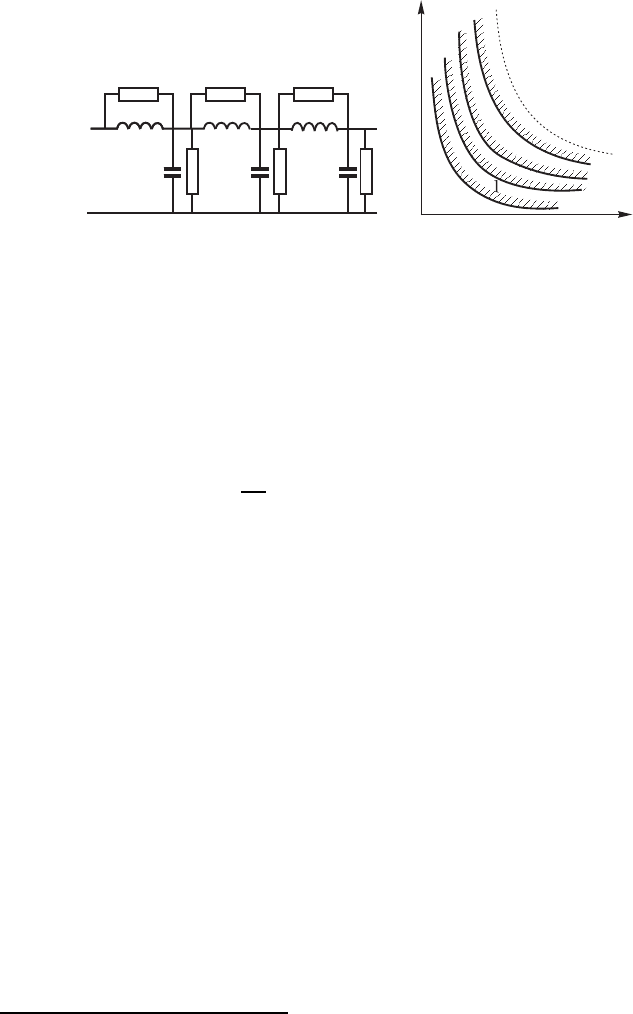
На рис. 14.2,б приведено разбиение плоскости параметров γ/ν, l на обла-

сти с различным порядком неустойчивости. В коротком резонаторе l <

кр

= 2π/

γ/ν возможна лишь статическая неустойчивость, так как в

правой полуплоскости плоскости p расположен только один корень — с

Im p = 0 (т.е. Re ω = 0), соответствующий экспоненциальному росту про-

странственно однородного поля. При увеличении l > l

кр

порядок неустой-

чивости растет, однако при любом конечном l число корней в правой

полуплоскости p всегда конечно.

Итак, когда речь идет об исследовании устойчивости ограниченных

распределенных систем (резонаторов), задача по сравнению с соответ-

ствующей сосредоточенной усложняется лишь тем, что спектр комплекс-

ных собственных частот оказывается счетным. При этом, перебирая все

возможные пространственные возмущения, т. е. все допустимые гранич-

ными условиями значения волновых чисел k

, мы, определив корни ха-

рактеристического уравнения D(ω, k), полностью решаем задач у об устой-

чивости. Здесь, конечно, могут встретиться трудности, но трудности тех-

нические.

Если же система полуограничена или безгранична, то сама постанов-

ка задачи об устойчивости, вообще говоря, не очевидна и требует допол-

нительных размышлений. Действительно, теперь, рассматривая устойчи-

вость возмущений в интересующей нас области пространства, мы должны

решить задачу об эволюции пространственно-локализованного возмуще-

335

g/n

D=0

àá

Рис. 14.2. Схема цепочки, соответствующей уравнению

(14.6) (а) и разбиение плоскости параметров λ/ν, l на обла-

сти с различным порядком неустойчивости (б)

ния — задачу с начальными условиями

u(x, t) =

2π

∞

−∞

(k, 0) e

i[ω

(k)t−kx]

dk , (14.7)

где u

(k, 0) — пространственный спектр начального возмущения, а сум-

мирование проводится по всем нормальным волнам. Как поведет себя

возмущение в заданной точке или локализованной области? Ведь экспо-

ненциальный рост во времени отдельных k-компонент пространственного

спектра отнюдь не гарантирует временного роста возмущения в этой точ-

ке или области. Действительно, возмущение может, нарастая во времени,

просто покидать рассматриваемую область, убегая из нее. Именно такая

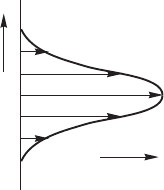
“сносовая”, или конвективная, неустойчивость наблюдается, например, в

некоторых сдвиговых гидродинамических течениях (в частности, затоп-

ленных струях (см. рис. 14.3), а также в различных электронных систе-

мах — лампе бегущей волны (ЛБВ), плазме, пронизываемой электронным

пучком, и т. д.

Если же среди нарастающих возмущений находятся такие, которые

не покидают заданной области, т.е. в каждой точке этой области воз-

мущение растет, то это уже истинная (см. общее определение, данное

выше) неустойчивость. Такую неустойчивость называют абсолютной

Впервые проблема разделения абсолютной и конвективной неустойчивостей была по-

ставлена Л.Д. Ландау и Е.М. Лифшицем [5] в связи с анализом гидродинамической

неустойчивости.

336

Рис. 14.3. Профиль скорости в затопленной струе

Формальные определения, следовательно, должны быть такими: если

lim

t→∞

u(x, t) → ∞ x ∈ (x

, x

) , (14.8)

где u(x, t) — возмущение (x

, x

— границы интересующей нас области, в

которой имеется неустойчивость), то неустойчивость — абсолютная; если

же

lim

t→∞

u(x, t) → 0 x ∈ (x

, x

) , (14.9)

то неустойчивость конвективная.

Естественно, что вид неустойчивости зависит от выбора системы ко-

ординат. Если мы движемся вместе с убегающим, растущим во времени

возмущением, то в новой системе координат неустойчивость будет уже

не конвективной, а абсолютной. И наоборот, если в системе с абсолют-

ной неустойчивостью перейти к новым переменным t

= t, x

= x − v

где v

превышает максимальную скорость распространения возмущений

(такой переход, конечно, (возможен не всегда; например, не имеет смы-

сла переходить в систему координат, движущуюся со скоростью, большей

скорости света), т о неустойчивость из абсолютной превратится в конвек-

тивную.

С проблемой разделения абсолютной и конвективной неустойчивости

тесно связана другая, может быть, даже более важная для приложений

проблема о распознавании усиления и непропускания в полуограничен-

ных системах, возбуждаемых сосредоточенным источником. Поясним эту

проблему подробнее.

Пусть на границу x = 0 среды, описываемой дисперсионным урав-

нением D(ω, k) = 0, подается сигнал. Для простоты будем считать его

радиоимпульсом с ч астотой заполнения ω

. Предположим далее, что кор-

ни уравнения D(ω

, k) = 0 не действительные, и пусть есть корни и с

337

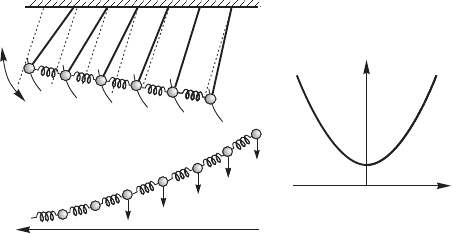
Рис. 14.4. Колебания (в плоскости, перпендикулярной ри-

сунку) в цепочке связанных маятников (а); дисперсионная

характеристики этой колебательной системы (б) и зату-

хание колебаний вдоль направления их распространения

(в) [6]

Im k < 0, и с Im k > 0. Что будет происходить с сигналом по мере рас-

пространения его в среде вдоль оси x? Казалось бы, поскольку решение

имеет вид

Im kx

iω

−i Re kx

при Im k > 0 сигнал должен нарастать вдоль x. Утверждение, вообще

говоря, неверно. Например, когда мы пытаемся возбудить колебания на

частоте ω < ω

в цепочке связанных маятников (рис. 14.4,а; дисперси-

онная характеристика этой системы приведена на рис. 14.4,б), мы полу-

чим не усиление колебаний вдоль оси x, а экспоненциальное затухание

(рис. 14.4,в). Колебание не возникает; в среде на закритической частоте

имеет место непропускание, хотя и в этом случае при ω < ω

имеется ко-

рень уравнения D(ω, k) = 0 с Im k > 0. В чем же дело? О твет заключается

в следующем: существование корня уравнения D(ω, k) = 0, лежащего в

верхней полуплоскости комплексной плоскости k, само по себе еще не

означает усиления. Волна, соответствующая этому корню, может распро-

страняться влево (Re k < 0), и тогда она будет затухать в направлении

своего распространения (рис. 14.4,в). В отличие от аналогичной задачи о

неустойчивости синусоидального решения во времени (в которой t всегда

растет), здесь оба направления изменения переменной x имеют смысл.

В этой главе мы обсудим различные примеры неустойчивых а усили-

вающих сред и сравнительно простые критерии, позволяющие отделить

338

усиление от непропускания и определить, какая неустойчивость реализу-

ется в системе — абсолютная или конвективная.

§ 2. Примеры волновых неустойчивостей: неустойчивость Джинса;

неустойчивость Тьюринга. Усиление в лампе с бегущей волной.

Условия самовозбуждения в лампе с обратной волной.

Неустойчивость Джинса— основная неутойчивость гравитирующих си-

стем.

Гравифизикой называют область науки, изучающую физическую эво-

люцию астрономических объектов под действием гравитационных сил.

Эволюция “классических” астрономических объектов

определяется Нью-

тоновыми силами тяготения, рассматривается в рамках нерелятивистской,

или классической, гравифизики.

Джинс рассмотрел в рамках уравнений гидродинамики устойчивость

самой простой, по его мнению, гравитирующей системы — бесконечно

протяженного по всем направления покоящегося в пространстве однород-

ного распределения гравитирующего газа (см., например, [7]). Исходя из

однородности и изотропии такого равномерно заполненного Ньютоновско-

го мира, Джинс принял, что гравитационная сила в любой точке равна

нулю и стационарна.

Гидродинамические уравнения для такой системы имеют вид:

∂ρ

∂t

+ v∇ρ = −ρ∇v ,

∂v

∂t

+ (v∇)v = −

∇p

− ∇Φ ,

∆Φ = 4πGρ ,

(14.10)

где ρ — плотность, v — скорость, p — давление, Φ — потенциал гравита-

ционного поля, G — гравитационная постоянная. Стационарные величины

будем отмечать индексом “0”, а малые отклонения от стационарных ве-

личин — значком “∼”. Будем считать, что до момента времени t = 0 (т.е.

при t < 0) система стационарна, причем v

= 0, а при t ≥ 0 массовая

плотность ρ(r, t) = ρ

+ ˜ρ(r, t), гравитационный потенциал Φ(r, t) = Φ

Φ(r, t), v(r, t) =

v(r, t). Используя введенные величины, запишем с

учетом системы уравнений (14.10) линеаризованные уравнения непрерыв-

К ним можоно отнести планеты, звезды, звездные скопления, галактики, их группы

и скопления.

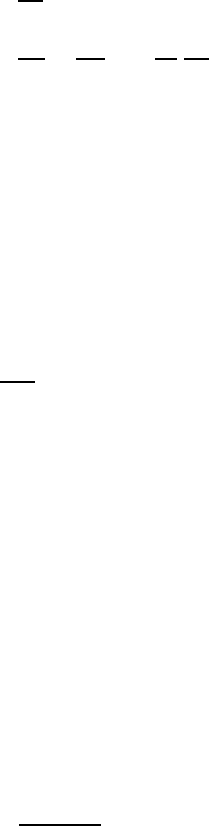
339

ности, движения, Пуассона и состояния:

∂ ˜ρ

∂t

+ div(ρ

v) = 0 , (14.11)

∂

∂t

∂

∂r

= −

∂ ˜p

∂r

, (14.12)

∆

Φ = 4πG˜ρ , (14.13)

˜p = c

˜ρ . (14.14)

При выводе уравнения состояния (14.14) использовано баротропное урав-

нение состояния p = p(ρ); c

= ∂p/∂ρ— квадрат изотермической скорости

звука.

Действуя оператором div на уравнение (14.12) и используя уравнения

(14.11) (при условии ρ

= const), (14.13) и (14.14), получаем следующее

волновое уравнение

∂

˜ρ

∂t

−



+ c

∆



˜ρ = 0 , (14.15)

где ω

= 4πGρ

. Коэффициенты уравнения (14.15) не зависят от коорди-

нат и времени, поэтому общее решение можно искать в виде:

˜ρ(r, t) =

k,ω

ρ(k, ω)e

i(ω

t−kr)

. (14.16)

Исходные уравнения (14.11)-(14.14) линейны т.е. справедлив принцип су-

перпозиции, и, следовательно, достаточно рассмотреть эволюцию произ-

вольно выбранной гармоники. В результате подстановки ее в уравнение

(14.15) находим дисперсионное уравнение:

= c

−ω

. (14.17)

Отсюда сразу видно, что при k

< 4πGρ

однородное распределение

плотности неустойчиво: ω

< 0. Н а нелинейной стадии процесса это при-

водит к возникновению гравитационных “капель” с пространственным

масштабом λ > λ

кр

πc

/Gρ

. Вид дисперсионных кривых уравне-

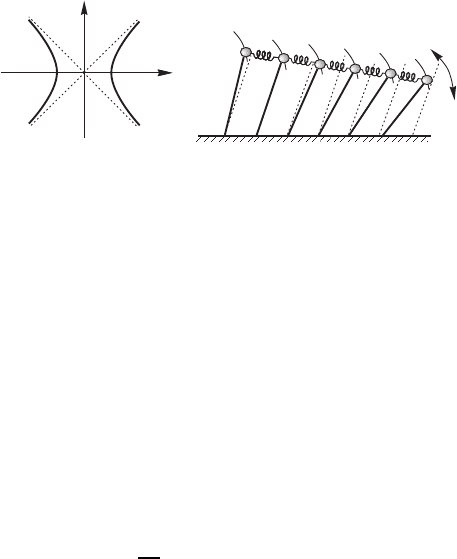
ния (14.17) приведен на рис. 14.5,а. Заметим, что закон дисперсии (14.17)

одновременно описывает и волновые возмущения в уже упоминавшейся

системе связанных маятников (в длинноволновом приближении), толь-

ко в отличие от рис. 14.4, в этом случае речь идет об устойчивости

стационарного состояния, в котором все маятники “стоят вверх ногами”

(рис. 14.5,б).

340

Рис. 14.5. Дисперсионные кривые уравнения (14.17) (а)

и описываемые этим уравнением колебания (в плоскости

перпендикулярной к рисунку) в системе связанных маят-

ников (б)

Таким образом, в рассматриваемой системе (14.10) имеется неустой-

чивость. Физический смысл условия λ > λ

кр

весьма прост: с увеличением

размера области возмущения гравитационная сила растет, а градиент дав-

ления падает. При λ = λ

кр

обе силы уравновешивают друг друга, а при

λ > λ

кр

гравитационная сила оказывается преобладающей.

Сделаем еще одно замечание. Запишем стационарные уравнения:

∇p

+ ∇Φ

= 0 , (14.18)

∆Φ

= 4πGρ

, (14.19)

= p(ρ

) . (14.20)

Из принятого Джинсом условия ρ

= const и уравнения (14.20) следует,

что первое слагаемое в уравнении (14.18) обращается в нуль и значит

= const. Подстановка последнего решения в уравнение (14.19) при-

водит к абсурду: ρ

= 0; откуда следует вывод об исследовании Джин-

сом устойчивости несуществующего стационарного состояния бесконечно

протяженной однородной среды. Как указано в [7], при анализе устойчи-

вости стационарного решения с Φ

= ϕ(r) вблизи центра ограниченной

области Φ

= const считается хорошим приближением.

Неустойчивость Тьюринга — пример д иффузионной неустойчивости

. В 1952 году Тьюринг рассмотрел модель кинетики химических реакций

с учетом диффузии.

В рамках этой модели обнаружилась неустойчивость, приводящая

к возникновению пространственных структур. По этой причине модель

Тьюринга и сходные с ней модели вызвали чрезвычайный интерес как мо-