Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

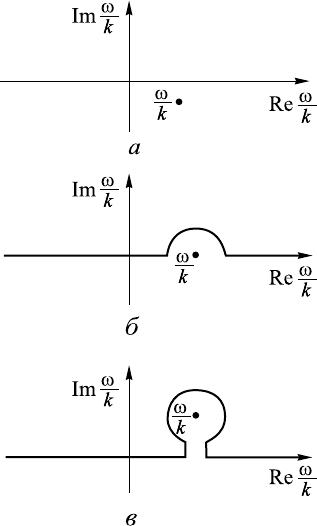
301

Рис. 12.4. Контуры интегрирования C, соответствующие правилу

Ландау обхода полюса.

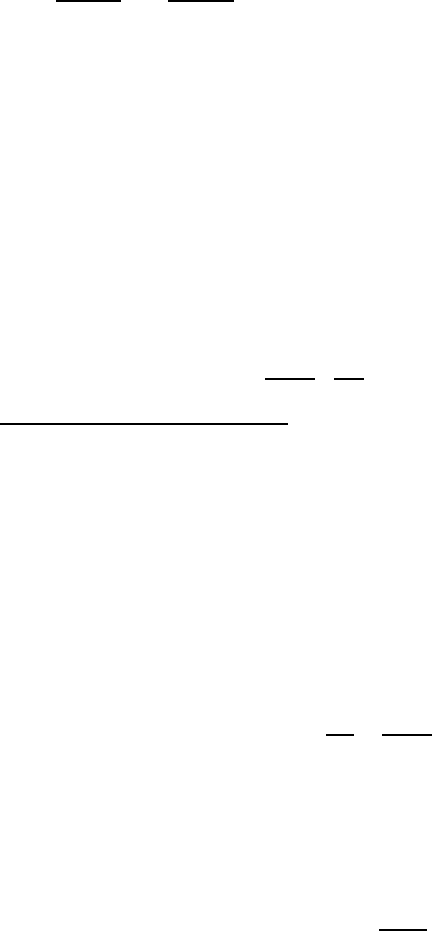
302

где P — главная часть интеграла берется вдоль веще ственной оси в точки

сингулярности v = ω/k

. Это можно записать также в виде

ω − kv

= P

ω − kv

+ iπδ(ω − kv) , (ω — вещественна) (12.36)

δ — дельта функция Дирака.

Возможна следующая интерпретация соотношения (12.35): вклад от

вычета — результат выбора ненулевой функции F в формуле (12.30), а

интеграл вдоль вещественной оси можно отождествить с частным реше-

нием (12.27). Тогда, если F ∼ e

−ikx

, то ее следует записать в виде:

F(vt − x) = e

ik(vt−x)

F (v) , (12.37)

где F(v) — произвольная функция . Сравнение этого выражения с пред-

ставлением (12.36) при вещественном значении ω/k показывает, что функ-

цию F нужно выбрать следующим образом:

F (v) = −

πE





v=ω/k

· δ(ω − kv) .

Напомним о сновные сведения о вычетах, необходимые для наших вычислений.

Пусть f(z) однозначная и аналитическая функция всюду на замкнутом контуре L (по

нему вычисляется

f(z) dz) и всюду внутри L, за исключением конечного числа точек

, z

, . . . , z

, расположенных внутри L, контур L ориентирован против часовой стрелки

(в положительном направлении). Тогда справедлива теорема Коши о вычетах:

f(z) dz = 2πi

k=1

Res

z=z

f(z) .

В правой части суммирование распространяется на все особые точки функции f(z), распо-

ложенные внутри L, если таких нет, то интеграл равен нулю. Из теоремы Коши вытекает

интегральная формула Коши:

f(z

) =

2πi

f(z)

z − z

dz ,

причем, f(z) — однозначная и аналитическая всюду внутри контура L и на нем, а точка

находится внутри L.

Если подынтегральная функция f(z) представляет собой отношение двух конечных

функций f(z) = g(z)/h(z), причем, в некоторой точке z = z

числитель отличен от нуля,

а знаменатель обращается в нуль по закону h(z) ∼ z − z

(полюс первого порядка), то

Res

z=z

f(z) =

g(z

)

где штрих означает производную по z.

303

Если ω находится в верхней полуплоскости, то интегрирование про-

водится по контуру, изображенному на рис. 12.4,в и

∞+iγ

−∞−iγ

−2πi Res( при v = ω/k) , (Im ω > 0 , γ > 0) . (12.38)

В этом случае выбор F (v) не столь очевиден.

В теории плазмы часто используется и другое представление отклика

плазмы на продольные поля. Уравнение Пуассона

div E

= 4π(ρ

плазм

− ρ

внеш

) ,

где ρ

плазм

= ηE

(см. формулы (12.32)), а ρ

внеш

— плотность заряда,

обусловленная каким либо сторонним источником, перепишем в виде:

div D = 4πρ

внеш

D = (εE

/4π). Тогда с учетом того, что все величины изменяются с коор-

динатой по гармоническому закону, “ диэлектрическая проницаемость” ε

представляет собой безразмерную величину

ε(ω, k) = 1 +

4πη

или ε(ω, k) = 1 +

4πσ

iω

. (12.39)

В такой трактовке заряды плазмы рассматриваются как источники по-

ляризации, а не токов, поэтому имеет место аналогия не с проводящей

средой, а с диэлектриком.

Предположим теперь, что поле E

, которое до сих пор считали задан-

ным, возникает за счет пространственного заряда самой плазмы. В рамках

одномерной линеаризованной модели уравнение Пуассона при ρ

внеш

= 0

примет вид:

−ikE

= 4πρ , (12.40)

где ρ — полная плотность пространственного заряда , создаваемая все-

ми составляющими плазмы. Будем далее для простоты считать, что ρ

определяется только электронной компонентой. Эт о означает, что тяже-

лые ионы неподвижны и нейтрализуют статический заряд электронов.

Согласно первому соотношению (12.32) и (12.40) имеем η = −ik/4π или

с учетом формулы (12.33) находим:

4πe

/dv

ω − kv

dv = −1 . (12.41)

304

В этом уравнении контур C выбран согласно правилу обхода Ландау, т.е.

вдоль вещественной оси, если Im ω < 0, и с обходом полюса сверху, если

Im ω ≥ 0. В силу первого уравнения из (12.39) уравнение (12.41) можно

записать и так:

ε(ω, k) = 0 . (12.42)

Будем считать величину k заданной, положительной и решать дисперси-

онное уравнение (12.41) относительно ω. Чаще всего это сделать непро-

сто, но при заданной f

(v) в принципе возможно.

Имеются ли решения с ω в нижней полуплоскости? Если да, то имеет

место неустойчивость и плазменные колебания возрастают экспоненци-

ально. В следующей главе покажем, что такая ситуация возможна, если,

например, f

состоит из двух δ-функций, соответствующих двум скоро-

стям потоков. Причем, при небольшом уширении распределения скоро-

стей при переходе к непрерывному распределению f

решение все еще

будет неустойчивым. Когда плазма с распределением скоростей f

бу-

дет устойчивой? Без доказательства примем, что достаточным условием

устойчивости является наличие у функции f

(v) не более одного макси-

мума, причем функция должна быть положительной и стремится к нулю

при v → ±∞. Заметим, что этим тре бованиям удовлетворяет распределе-

ние Максвелла

(x, v, t) = n

(2πk

T )

−

m(v−u)

2kT

, (12.43)

где k

— постоянная Больцмана, T — температура, n — концентрация ,

u — скорость дрейфа компонент плазмы; при этом для двухкомпонентной

плазмы, состоящей из однократно заряженных ионов (i) и электронов (e)

v =

v = n , (12.44)

v =

v = nu . (12.45)

Далее для удобства выберем систему отсчета, в которой в среднем

электроны покоятся, а f

(v) соответствует устойчивой плазме.

Перепишем уравнение (12.41) в виде:

D(ω, k) = 0 , (12.46)

305

где

D(ω, k) =

/dv

ω/k − v

dv +

4πe

. (12.47)

Как показано выше в рамках гидродинамической т еории (см. форму-

лу (12.11)) для холодной неподвижной плазмы дисперсионное уравнение

имеет вид: ω

= ω

, а учет тепловых скоростей при kr

 1 (r

 λ),

дает малую поправку к ω

, выражаемую соотношением (12.12). Если

 1, многие электроны успевают пройти за период колебания рас-

стояние в одну длину волны и больше, вследствие чего сжатие перестает

быть адиабатическим. Кинетическая теория соответствует физике таких

колебаний. Разумно проанализировать, что дает кинетическая теория по

сравнению с гидродинамической в том же длинноволновом пределе.

Предположим, что имеет место разброс тепловых скоростей с некото -

рым характерным значением тепловой скорости v

, таким, что |v|  v

и при этом функция f

(v) очень мала. В этом случае влияние теплового

разброса пренебрежимо мало, если фазовая скорость волны ω/k  v

так что практически все частицы неподвижны. В силу того, что при этом

ω ∼ ω

, можно считать ω

/k  v

, то k  ω

. Но радиус Дебая

T/m

, а k

T ∼ m

; иными словами r

∼ v

/ω

и kr

 1

 λ), что и соответствует длинноволновому приближению. Уже ука-

зывалось, что функция f

(v), будучи устойчивым распределением, моно-

тонно спадая при |v|  v

, обращается в нуль лишь при v → ±∞. Пусть

также ведет себя и df

/dv. При этом решения с вещественными ω от-

сутствуют, поскольку в этом случае главная часть интеграла (см. форму-

лу (12.35)) дает вещественный вклад в (12.47), а вычет — чисто мнимый.

Поэтому положим ω = ω

+ iγ, где (ω

−ω

) и γ — малые поправки к ве-

щественной и мнимой частям ω, соответственно, что позволяет вычислить

их методом последовательных приближений. В большинстве интересных

случаев выполняется неравенство γ  |ω

− ω

|, поэтому в первом при-

ближении можно пренебречь вычетом и решать уравнение D(ω, k) = 0,

оставляя только главную часть интеграла. Разложим подынтегральное

306

выражение в (12.47) в ряд по kv/ω. Тогда

∞

−∞

/dv

(ω/k − v)

dv =

∞

−∞

/dv

(1 − kv/ω)

dv =

∞

−∞

1 +





+ . . .

dv . (12.48)

Возьмем этот интеграл по частям, что дает

∞

−∞

/dv

(ω/k − v)

dv =

∞

−∞

1 + 2

+ 3





+ . . .

dv . (12.49)

Интегрируя правую часть (12.49) почленно и учитывая, что n =

dv и

T =

dv, окончательно находим

D(ω, k) =

4πe

−



1 +

mω

+ . . .



. (12.50)

Как и следовало ожидать, в первом приближении уравнение D(ω, k) = 0

дает ω

= ω

(ω

= 4πne

/m), а в следующем приближении ω

= ω

(1 +

+ 3k

), если положить ω = ω

в поправочном члене. Иными словами,

получили полное совпадение с гидродинамической теорией. Процесс на-

хождения поправок можно продолжить и дальше (на каждом шаге ω

является вещественной), но до тех пор пока можно пренебрегать вкла-

дом от вычета. Вычислим теперь и вычет. Напомним, что было сделано

предположение γ  |ω

−ω

|. Э то означает, чт о поправка, вносимая слага-

емым iγ в ω меньше, чем вещественные поправки, которые вычислялись

до сих пор. Величина ω

найдена уже с достаточной степенью точности.

Вычисляя D(ω, k) при ω = ω

, получим

D(ω, k) = P [D(ω, k)] + iπ





v=ω

(символ P [D(ω, k)] обозначает величину D(ω, k), найденную без учета

вклада от вычета). Очевидно тогда, что

D(ω

+ iγ, k) = P[D(ω

, k)] + iπ





v=ω

+ iγ



∂D

∂ω



ω=ω

. (12.51)

Следует заметить, что введенная выше температура T соответствует продольному

движению и отличается от полной температуры, если распределение анизотропно.

307

Если D = D

+ iD

, то

iγ



∂D

∂ω



ω=ω

= γ



∂D

∂γ

+ i

∂D

∂γ



ω=ω

Действительная часть этого выражения дает небольшую поправку к ω

которой можно пренебречь. Мнимая часть должна сократиться с вычетом

в (12.51) , если при подправленной частоте по-прежнему D = 0.

В соответствии с условиями Коши-Римана (см. сноску на стр. 300)

∂D

/∂γ = ∂D

/∂ω

, так как D а налитическая функция. Тогда

γ = −π





v=ω



∂D

∂ω



−1

. (12.52)

Величину ∂D

/∂ω

можно вычислить, используя, что при веществен-

ных ω величина D

= P(D). Пусть функция ω

(k) определяется уравнени-

ем D

= 0 (именно эту функцию мы определяем методом последователь-

ных приближений (см. соотношение ω

= ω

(1+3r

))). Дифференцируя

= 0, получим

∂D

∂k

∂D

∂ω

= 0 . (12.53)

Из формулы (12.47) следует, что

∂D

∂k

2mk

4πe

−

∂D

∂ω

. (12.54)

Из соотношений (12.53) и (12.54) следует



dω

−



∂D

∂ω

= −

2mk

4πe

. (12.55)

Тогда с учетом (12.55) выражение (12.52) принимает вид:

γ = −

2π





v=ω



−

dω



. (12.56)

В первом приближении ω

= ω

и dω

/dk = 0, и приходим к результату

полученному впервые Ландау (Ландау Л.Д., ЖЭТФ, 1946, т.16, с.574).

Поскольку df

/dv < 0, γ > 0 и волна, содержащая множител ь e

−γt

зату-

хает. Этот эффект называется “ затуханием Ландау”.

308

exp(

mv

2kT

)

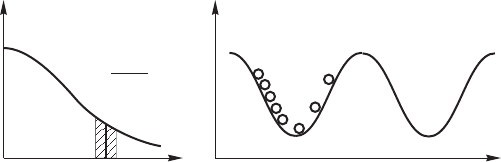
Рис. 12.5. К объяснению затухания Ландау: а — распределение

электронов по скоростям (заштрихованная область соответствует

резонансным электронам (v

∼ v

)); б — модель движения резо-

нансных электронов в поле плазменной волны, если v

< v

, но

одного порядка; большая часть электронов группируется на уско-

ряющем склоне потенциального “горба” плазменной волны.

Качественное объяснение эффекта состоит в том, что, если скорость

электронов меньше фазовой скорости волны, но близка к ней, электро-

ны забирают энергию у волны и колебания затухают. Чем больше будет

таких резонансных частиц, тем больше будет затухание. Если функция

распределения для плазмы монотонно спадает со скоростью df

/dv < 0,

то электронов, отстающих от волны будет больше, чем обгоняющих (от-

дающих энергию). Сказанное иллюстрируется на рис. 12.5.

В том случае, если скорость электронов больше фазовой скорости

волны (но по — прежнему близка к ней) и df

/dv > 0 для этой скорости,

волна будет усиливающейся, что связывают с черенковским излучением

плазменных волн резонансными частицами. Затухание Ландау и эффект

Черенкова, в известном смысле, — два явления, обратных друг другу,

поскольку они тесно связаны условием ω = kv.

§ 5. Дисперсия волн в двухжидкостной гидрод инамике. Ионно —

звуковые волны.

Будем исходить из уравнений двухжидкостной гидродинамики, счи-

тая, как и прежде, что T

 T

, магнитные поля отсутствуют, столкнове-

ниями можно пренебречь, и, кроме того, пренебрежем инерцией электро-

нов в уравнении (12.5), т.е. пренебрегаем слагаемым ∂v

/∂t + (v

∇)v

Тогда в одномерном случае из уравнений (12.3)-(12.7) получим следую-

309

щую систему:

∂v

∂t

= −

∂ϕ

∂x

, 0 = −

∂

∂x

) +

∂ϕ

∂x

∂

∂x

= −4πe(n

− n

) ,

∂n

∂t

∂

∂x

) = 0 .

Пусть электроны имеют постоянную температуру, т.е. T

= const. Тогда

из второго уравнения в линейном приближении имеем, что

)∂n

/∂x = e∂ϕ/∂x ,

где n

= n

+ n

 n

), и, следовательно, первое уравнение можно

переписать в виде ∂v

/∂t = −[k

/(m

)]∂n

/∂x. Из третьего уравне-

ния имеем n

= n

− [1/(4πe)]∂

ϕ/∂x

, или, используя выражение для

∂ϕ/∂x, находим, что n

= n

− [1/(4πn

)]∂

/∂x

. Окончательно пре-

образованную систему уравнений можно записать так:

∂v

∂t

∂n

∂x

= 0 ,

∂n

∂t

+ n

∂v

∂x

= 0 ,

= n

−

4πn

∂

∂x

(12.57)

Сравнивая систему уравнений для длинной линии, ячейка которой пред-

ставлена на рис. 12.6 с системой уравнений (12.57), легко установить

между ними прямое соответствие [6].

Для наглядности выпишем параметры и величины: для длинной линии

u , I , I

, L , C

, C ,

√

LC = ω

, 1/k

= c

/c ∼ (∆x)

;

для плазмы

, n

, 1/n

, m

/(4πe

) , m

/(k

) ,

(4πn

)

1/2

= ω

, 1/k

= k

/(4πn

) = r

Подчеркнем, что размер ячейки длинной линии (∆x) соответствует ради-

усу Дебая для плазмы.

310

Рис. 12.6. Длинная линия с индуктивной связью M, моделирую-

щая ионный звук в плазме.

Полагая, что все возмущения распространяются в виде плоских волн

вида exp[i(ωt − kx)], из (12.57) можно найти дисперсионное уравнение

= ω

/(k

+ k

) или

1 + k

, (12.58)

где c

— скорость ионного звука. Если kr

 1, то ω = c

С ростом k ч астота начинает расти медленнее, чем по линейному закону,

фазовая скорость волны начинает падать; v

→ 0 при k → ∞. Физически

дисперсия ионного звука связана с тем, что колебания ионов происхо-

дят при неподвижных в среднем электронах: давление последних ком-

пенсирует действие электрического поля, не давая электронам смещать-

ся. Дисперсия имеет место в области высоких частот. Приведем в каче-

стве аналогии с длинной линией результаты эксперимента [6]. Разрядная

трубка, использованная в эксперименте, схематически представлена на

рис. 12.7,а. Между подвижными сеткой и анодом возбуждались стоячие

волны; с помощью зонда приводился анализ возникших колебаний. Бы-

ли обнаружены ионные звуковые волны с частотой f

кол

∼ 2

(L — характерный размер плазмы, например длина трубки или расстояние