Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

291

получаем

∂v

∂t

+ (v

∇)v

= −

∇n

−

∇ϕ +

e,i

−

B] . (12.4)

По аналогии для электронного компонента имеем

∂v

∂t

+ (v

∇)v

= −

∇n

−

∇ϕ −

e,i

−

B] . (12.5)

Уравнения (12.4) и (12.5) — уравнения Эйлера для двух заряженных

взаимопроникающих жидкостей, ко торые взаимодействуют между собой

благодаря трению и через самосогласованное электрическое поле. Если

плазма сохраняет квазинейтральность и ионы однозарядные, то n

≈ n

= n. В этом случае можно перейти к модели одножидкостной гидроди-

намики, сложив уравнения (12.4) и (12.5) . Тогда, если пренебречь силой

Лоренца, получим

∂v

∂t

+ (v∇)v] = −∇[nk

+ T

)] , (12.6)

где v = v

+ (m

≈ v

(слагаемые, связанные с силами <<электри-

ческого трения>> и трения из -за столкновений, взаимно уничтожились).

Для электронной и ионной жидкостей должны также выполняться

уравнения непрерывности

∂n

∂t

+ div n

= 0 , (12.7)

∂n

∂t

+ div n

= 0 . (12.8)

При выводе предполагалось, что процессами ионизации и рекомбина-

ции можно пренебречь.

§ 3. Дисперсионное уравнение для плазменных ленгмюровских ко-

лебаний и анализ важных частных случаев.

Предположим, что все электроны в тонком слое холодной бесстолк-

новительной безграничной плазмы (T

= T

= 0 , F

= F

= 0) внезапно

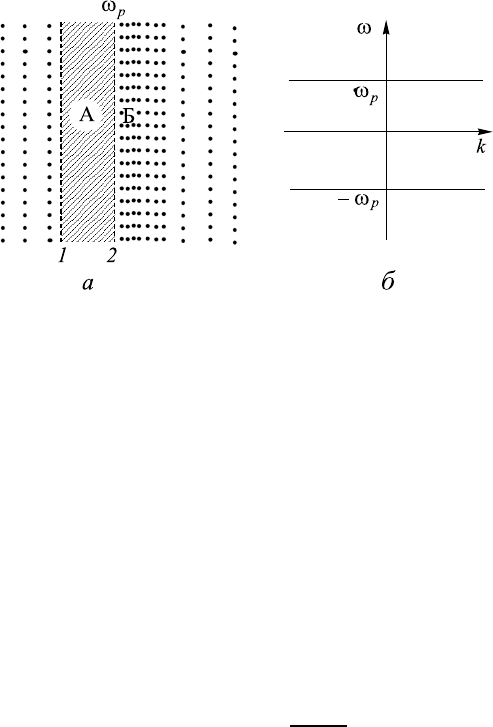
смещены вправо так, что между плоскостями 1 и 2 на рис. 12.1,а электро-

нов нет. Ионы плазмы будем считать неподвижными. Справа от плоскости

2 будет избыток заряда, что приведет к возникновению возвращающей си-

лы F

= −eE

обусловленной декомпенсацией зарядов. Величину E

мы

292

уже оценивали: если электроны сместились на x т о F

≈ −4πne

. Эта

сила сообщает им ускорение −(4πne

, поэтому движение группы

смещенных электронов описывается уравнением гармонических коле ба -

ний с плазменной частотой ω

¨x

+ ω

= 0 .

. Такие колебания называются плазменными или ленгмюровскими колеба-

ниями в “холодной” бесстолкновительной непод вижной плазме. О пишем

их с помощью уравнений (12.4)-(12.8). Будем полагать, что магнитное

поле равно нулю; столкновениями можно пренебречь; ионы не уч аству-

ют в колебаниях и являются однородным компенсирующим неподвижным

фоном (m

 m

); плазма представляет собой одномерный поток электро-

нов, движущийся со скоростью v

= const в направлении оси x. Учтем

также влияние сил, связанных с перепадом давления в плазме, т. е. вли-

яние звуковых эффектов. Допустим, чт о начальное возмущение имеет

вид пло ской волны с частотой ω и волновым числом k (f

∼ exp[i(ωt −

− kx)]). Для малых возмущений давление электронной жидкости p

= p

+ p

, концентрация n = n

+ n

, скорость электронной жидкости

v = v

+ v

(все возмущенные величины, много меньшие соответству-

ющих невозмущенных). Давление электронной жидкости представим в

виде p

+ n

) = p

+ m

(∂p

/∂ρ

(ρ — плотность электронного газа)

и ∇p

= m

(∂p

/∂ρ

)(∂n

/∂x). При сделанных допущениях из уравне-

ний двухжидкостной плазменной гидродинамики (12.4), (12.5) получим

следующую систему:

∂v

∂t

+ v

∂v

∂x

= −

∂p

∂ρ

∂n

∂x

∂ϕ

∂x

= 0 ,

∂

∂x

= 4πen

∂n

∂t

+ n

∂v

∂x

+ v

∂n

∂x

= 0 .

Подставляя в эти уравнения v

, n

, ϕ

∼ exp[i(ωt − kx)], из условия сов-

местности получившейся алгебраической системы находим закон диспер-

сии ленгмюровских волн:

(ω − kv

)

= ω

+ k

∂p

∂ρ

. (12.9)

Это уравнение при v

= 0 соответствует дисперсионному уравнению ω

= ω

+ k

/(LC) для цепочки связанных маятников (см. рис. 12.2). По-

добное (12.9) уравнение было получено впервые Ленгмюром, который ис-

ходил из аналогии со звуковыми волнами в воде (11.12). Здесь осталась

293

Рис. 12.1. К объяснению ленгмюровских плазменных колебаний;

а — все электроны в тонком слое внезапно смещены вправо (А—

область, где электронов нет; Б — область с избытком электронов);

б — дисперсионная кривая ω

= ω

неизвестной величина ∂p

/∂ρ. Чтобы замк нут ь уравнения гидродинами-

ки, будем считать давление электронной жидкости изотропным и связан-

ным с концентрацией уравнением состояния p

= const, но p

= nk

поэтому ∂p

/∂ρ

= γp

/(nm

)(ρ

= m

n). Как следует из кинетической

теории [2], γ = 3 т.е. ∂p

/∂ρ

= 3k

. Уравнение p ∼ n

является

уравнением состояния газа в случае одномерного адиабатического сжатия

и может быть получено из термодинамики. С учетом сказанного из (12.9)

окончательно имеем

(ω − kv

)

= ω

. (12.10)

Задача 12.1. В книге [1] для модели, в которой газ находится в среде с дву-

мя параллельными плоскими стенками, расстояние между которыми мед-

ленно изменяется, уравнение p ∼ n

получено из оценочных соображений,

основанных на сохранении адиабатического инварианта v

⊥

l = const, где

⊥

— компонента скорости частицы, перпендикулярная стенке, l — расстоя-

ние между стенками. Попытайтесь рассмотреть эту модель самостоятельно.

Формула v

⊥

l = const легко доказывается, если рассмотреть отражение ча-

стиц от неподвижной стенки.

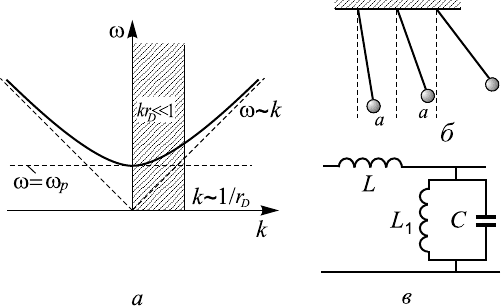
График закона дисперсии для среды из осцилляторов, соответствую-

щий уравнению (12.10) при v

= 0, показан на рисунке 12.2. Остановимся

более подробно на анализе (12.9) для различных частных случаев.

294

Рис. 12.2. Закон дисперсии для плазмы, представляющей собой

среду с дисперсией в области низких частот; показана граница

по k справедливости гидродинамической теории (kr

 1) (а).

Механический (б) и электрический (в) аналоги волн в плазме

(см. 13.10)

Плазменные колебания в “холодной” неподвижной плазме. Диспер-

сионное уравнение получается из (12.9) при T

= 0 и v

= 0 и имеет уже

известный нам вид ω

= ω

(см. рис 12.1,б). В “холодной” плазме ленг-

мюровские колебания не обладают дисперсией, и, если плазма покоится,

они не распространяются, поскольку v

гр

= dω/dk = 0. Следует, однако,

заметить, что фазовая скорость отлична от нуля и равна v

= ω/k = ω

(k — волновое число плоской волны возмущений).

Плазменные колебания в одномерном “холодном” потоке (v

6= 0 , T

= 0). Из (12.9) находим, что

(ω − kv

)

= ω

(12.11)

Легко видеть, что решением уравнения (12.11) являются широко исполь-

зуемые в CВЧ – электронике [4] волны пространственного заряда: мед-

ленная с k = ω/v

− ω

и быстрая с k = ω/v

+ ω

(рис. 12.3).

Плазменные колебания в одномерном “холодном” потоке представляют

собой только что рассмотренные ленгмюровские колебания, которые пе-

реносятся электронами с дрейфовой скоростью v

. Поэтому волны про-

странственного заряда часто называют электрокинематическими.

295

Рис. 12.3. Дисперсионные кривые для холодного одномерного

электронного потока

Плазменные колебания в неподвижной “горячей” плазме(T

6= 0 , v

= 0). Перепишем (12.9) при v

= 0 в виде

= ω

(1 + 3k

) , (12.12)

где r

= (k

)

1/2

— радиус Дебая (см. (12.1)). Дисперсионное

уравнение (12.12) справедливо только для длинноволновых возмущений,

когда kr

 1 или r

 λ. Электроны смещаются за период 2π/ω на

расстояние, меньшее, чем длина волны; сжатие должно быть адиабати-

ческим. Напомним, что мы раскладывали правую часть уравнения со-

стояния в ряд и ограничивались одним членом разложения, поэтому и

дисперсионное уравнение (12.12) имеет вид аналогичного разложения по

малому параметру kr

. Учет конечной температуры электронов в этом

приближении дает лишь поправку к т еории “холодной” плазмы. Легко

видеть, что v

гр

= 3ω

1 + 3k

, откуда при условии применимо-

сти рассмотрения (kr

 1) имеем

гр

≈ 3kr

. (12.13)

Величина

имеет порядок тепловой скорости электронов, по-

этому групповая скорость волн в неподвижной “горячей” плазме, как это

видно из (12.13), много меньше тепловой. Так им образом, волна перено-

сит энергию через “горячую” плазму в отличие от предыдущего случая,

где групповая скорость просто равнялась дрейфовой.

296

§ 4. Элементы кинетической теории плазмы

(плазма в продольном электрическом поле;

плазменные колебания и затухание Ландау).

Рассмотрим функцию f (x, v, t), где x — координата, v — скорость

частицы, так что fd

v — число частиц в области (x, x + dx), (v, v +

+ dv) фазового пространства. Она удовлетворяет закону сохранения

∂f

∂t

∂

∂x

f) +

∂

∂v

f) = 0 (12.14)

(см., например, [5]). В уравнении (12.14) нижние индексы обозначают

декартовы компоненты, а суммирование ведется по k = 1, 2, 3 . Пусть

a(x, v, t) — ускорение частицы, имеющей в точке x скорость v, причем,

для частицы с массой m и зарядом e в электрическом поле E и магнитном

поле B

a =



E +

[vB(x, t)]



, (12.15)

где квадратные скобки означают векторное произведение. Для л юбого

ускорения, выражаемого формулой (12.15), ∂a

/∂v

= 0, поэтому уравне-

ние (12.14) можно переписать в виде :

∂f

∂t

+ v

∂f

∂x

+ a

∂f

∂v

= 0 , (12.16)

которое в литературе (см., например, [5]) называют уравнением Больц-

мана — Власова.

При статистическом подходе функция f должна быть гладкой, т.е.

дифференцируемой, функцией, которую будем обозначать

. В данном

рассмотрении функция

f имеет смысл только в применении к достаточ-

но большому объему фазового пространства d

x d

v, ко торый содержит

очень большое число частиц. При этом

f d

x d

v есть среднее (а не точ-

ное) число частиц в этом объеме. Представляется разумным и выражение

для полей в формуле (12.15) заменить сглаженными функциями

E(x, t)

B(x, t). Тогда окончательно имеем :

∂

∂t

+ v

∂

∂x

+ ¯a

∂

∂v

= 0 , (12.17)

При точном описании функция f(x, v, t) представляет собой совокупность δ — функ-

ций (по одной на каждую частицу). Ускорение a после учета собственного поля частицы

должно определятся действием полей всех остальных частиц и полем внешнего источни-

ка, если такой есть. Иными словами, уравнение (12.16) при таком рассмотрении пригодно

для р ешения задачи об определении траекторий частиц.

297

где

a =



E +



B(x, t)





. (12.18)

Если заряженных частиц несколько сортов s, то нужно использовать

функцию

f для каждого сорта (

). При этом уравнение (12.17) будет

справедливо для каждого сорта частиц.

Очевидно, что плотность объемного заряда и плотность тока для s-го

сорта заряженных частиц имеет вид:

¯ρ

= e

v , (12.19)

= e

v . (12.20)

Систему уравнений (12.17)-(12.20) замыкают уравнения Максвелла, в ко-

торые могут входить плотности заряда ρ

внеш

и т ока

j, создаваемые внеш-

ним источником (если он есть). Чтобы применять уравнения (12.17) к

“сглаженным” функциям распределения и компонентам электромагнит-

ного поля, необходимо предположить, что сила, действующая на любую

частицу, является непрерывной и медленно меняющейся в пространстве

функцией, описывающей влияние всех остальных частиц на данную. Это

справедливо практически для всех частиц, кроме расположенных вблизи

от выбранной: для них изменения поля в рассматриваемой области фи-

зического пространства могут быть достаточно быстрыми. Между таки-

ми близко расположенными частицами могут происходить столкновения.

Уравнение (12.17) можно с хорошим приближением применять только в

случае, когда вклад от столкновения с одной или небольшим числом

близлежащих частиц пренебрежимо мал по сравнению с коллективным

влиянием далеких частиц. Поэтому уравнение (12.17) называют “Бес-

столкновительным уравнением Больцмана — Власова” [5]. Заметим, что

использованные ранее гидродинамические уравнения могут быть получе-

ны при определенных условиях из уравнения (12.17) (см., например, [5]).

В векторной форме бесстолкновительное уравнение Больцмана — Власова

можно записать в виде

∂f

∂t

+ v

∂f

∂x



E +

[vB]



∂f

∂v

= 0 , (12.21)

заряд выбран как +|e|, черта над всеми величинами опущена. В невозму-

щенном состоянии E = 0, B = B

— однородное магнитное поле ) и

298

для каждого сорта частиц f = f

во всем пространстве. При этом функ-

ция f

зависит только о т v, а суммарные плотность заряда и тока равны

нулю. В этом случае из уравнения (12.20) находим, что

[vB

]

∂f

∂v

= 0 . (12.22)

Если предположить существование малого возмущения, то

f = f

+ f

, B = B

+ B

, E = E

, (12.23)

где f

, B

, E

— малые возмущения. С учетом (12.23) и малости возму-

щений (следует пренебречь квадратами, произведениями и более высоки-

ми степенями возмущенных величин) линеаризованное уравнение (12.21)

перепишем так:

∂f

∂t

+ v

∂f

∂x

[vB

]

∂f

∂v



[vB

]



∂f

∂v

= 0 . (12.24)

Будем искать решения уравнения (12.24) в виде

, E

, B

∼ e

i(ωt−kx)

(12.25)

и в большинстве случаев опускать в формулах экспоненциальный мно-

житель. Пусть далее E

параллельно k, и оба вектора направлены вдоль

оси x; B

= B

= 0

. Задача в этом случае становится одномерной и

уравнение (12.24) принимает вид:

∂f

∂t

+ v

∂f

∂x

= −

∂f

∂v

. (12.26)

Сначала предположим для простоты, что E

— заданное внешнее по-

ле, т.е. правая часть уравнения (12.26) известна. Используя в уравне-

нии (12.26) зависимости (12.25) находим, что

ieE

∂f

/∂v

ω − kv

. (12.27)

При этих допущениях y- и z- компоненты скорости каждой частицы остаются по-

стоянными, и их распределение не сказывается на результатах. Можно проинтегрировать

уравнение (12.21) по v

, рассматривая распределение лишь продольной скорости. Тогда

прод

(x, v

, t) =

f dv

Задача стала одномерной и индекс “прод.” и у f

, и у f

можно опустить.

299

Это “вынужденное” решение уравнения (12.26), которое разумно допол-

нить решением соответствующе го однородного уравнения

∂f

∂t

+ v

∂f

∂x

= 0 . (12.28)

Решение последнего можно представить в виде:

(x, v, t) = F(vt − x, v) , (12.29)

где F — произвольная вещественная функция своих аргументов. Это ре-

шение соответствует потоковому переносу возмущения частицами, сво-

бодно движущимися с постоянной скоростью. Окончательно общее ре-

шение уравнения (12.26) запишем так:

(x, v, t) =

ieE

∂f

/∂v

ω − kv

i(ωt−kx)

+ F(vt − x, v) , (12.30)

где F определяется начальными условиями. Как правило, интерес пред-

ставляет не сама функция f

, а плотность заряда и тока

ρ = e

dv , J = e

dv . (12.31)

Выберем в решении (12.30) функцию F пропорциональной величине

, сохраняя в ρ и J зависимость e

i(ωt−kx)

. Тогда ρ и j становятся про-

порциональными E

, т.е.

ρ = η(ω, k)E

, J = σ(ω, k)E

, (12.32)

где функции η и σ могут быть комплексными.

Принцип причинности налагает на эти функции ряд условий, которые

должны обеспечивать реакцию плазмы ка к следствие на вызывающий ее

источник для того, чтобы гармонические решения при сложении давали

реально существующе е возмущение. Если источник равен нулю при всех

t < 0, то нулю должна быть равна и реакция.

Пусть величина k — вещественная, а ω — комплексная и лежит в

нижней полуплоскости (ω/k). В этом случае величины, пропорциональ-

ные e

iωt

, не только осциллируют, но и экспоненциально нарастают во

времени. Это можно интерпретировать так: возмущающе е поле включили

в бесконечно далеком прошлом, когда плазма была невозмущенной, и оно

возросло до значения, соответствующего настоящему моменту времени.

Тогда функцию F для соблюдения принципа причинности нужно выбрать

300

равной нулю, иначе f

не обратится тождественно в нуль при t → −∞.

Результирующие значения η и σдолжны быть аналитическими функция-

ми ω, и в нижней полуплоскости ω не должно быть полюсов, потому что

они приведут к неустойчивости

Проведем вычисления, качественно описанные выше, для соотноше-

ния (12.30). При Im ω < 0 и действительном k положим F = 0. Тогда из

соотношений (12.31) и (12.32) с учетом (12.30) находим:

η =

∞

−∞

/dv

ω − kv

dv , (12.33)

σ =

∞

v(df

/dv)

ω − kv

dv . (12.34)

В выражениях (12.33) и (12.34) подынтегральные выражения имеют

особенность при v = ω/k, но она “не страшная”, поскольку полюс на-

ходится ниже контура интегрирования, ка к показано на рис. 12.4,а. Ве-

личину k можно без потери общности считать положительной. Устремим

теперь Im ω к нул ю. Тогда условие аналитичности η и σ требует обхода

полюса сверху, как показано на рис. 12.4,б. Если Im ω > 0 и поле затуха-

ет, то контур интегрирования становится таким, как на рис. 12.4,в. Иногда

выбор контура в зависимости от Im ω называют правилом Ландау обхода

полюсов. Если df

/dv — аналитическая функция комплексной величины

v, то правило обхода дает необходимое аналитическое продолжение по ω

для функций η и σ.

При веще ственном значении ω интегрирование проводится по контуру,

показанному на рис. 12.4,б, и результат интегрирования можно записать

в виде:

= P

∞

−∞

− iπ Res( при v = ω/k) (ω— вещественна) , (12.35)

Напомним, что функция f(z), где z = Re z + i Im z = x + iy, называется аналити-

ческой, если существует производная f

(z) = df/dz, Если записать f(z) в виде f(z) =

= u(x, y)+ iv(x, y), то для аналитической функции выполняются условия Коши — Римана:

∂u

∂x

∂v

∂y

∂v

∂x

= −

∂u

∂y