Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

311

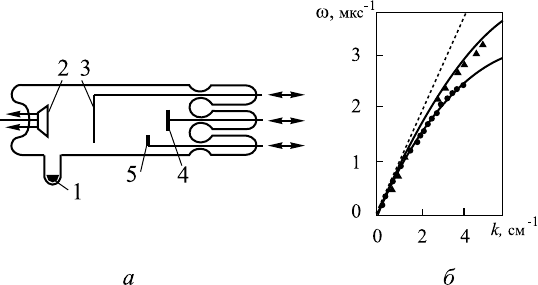
Рис. 12.7. Схема разрядной трубки (знаком ←→ отмечен подвиж-

ной электрод: 1 — ртуть; 2 — к атод; 3 — сетка; 4 — анод; 5

— зонд Ленгмюра (а) и измеренные экспериментально дисперси-

онные кривые для двух значений тока разряда (кружки — I

= 10 мА; треугольники — I

= 16 мА; штриховая линия — рас-

четная прямая по уравнению ω = ω

k/k

(б)) [6].

между электродами). Результаты эксперимента приведены на рис. 12.7,б.

До сих пор, говоря о плазме, мы имели в виду ионизованный газ. В

последние годы широко исследуется плазма твердого тела. В частности,

плазма полупроводников и металлов определяется как совокупность по-

движных электронов и дырок, а также ионизованных атомов, связанных

с кристаллической решеткой. Коллективные колебания в твердотельной

плазме имеют много общего с рассмотренными нами колебаниями газо-

разрядной плазмы [7–9].

ГЛ АВА 13

Кинематика волнового движения.

О различных способах введения понятия групповой скорости.

Скорость распространения энергии. Два парадокса Л.И. Ман-

дельштама, которые возникают, если не принимать во вни-

мание различие понятий фазовой и групповой скорости. Фа-

зовая, групповая и скорость распространения энергии волн в

некоторых сплошных с редах.

§ 1. О различных способах введения понятия групповой

скорости. Скорость распространения энергии.

В главе9 было дано напоминание волновой терминологии и обсуждены

понятия фазовой и групповой скорости в простых ситуациях, когда до-

полнительные разъяснения не нужны. Однако, в случаях активной среды

или содержащей переменные параметры вопрос о скоростях распростра-

нения волн требует обсуждения (см., например, [1–4]). Будем далее в

изложении в основном следовать книге [5].

Если изменение некоторой функции, характеризующей волновой про-

цесс, можно представить в виде u(x, t) = u

Re{exp[i(ωt −kx)]}, где u

= const, то такая монохроматическая волна распространяется со скоро-

стью

(13.1)

Это — фазовая скорость волны, которая определяет скоро сть отдель-

ного гребня, впадины или узла волны u(x, t). Если ввести фазу ϕ =

= ωt − kx, л инейную по независимым переменным, то ϕ = const для

наблюдателя, движущегося со скоростью v

. Действительно, dϕ/dt =

= ∂ϕ/∂t + (dx/dt)∂ϕ/∂x = 0, когда dx/dt = v

, поскольку по опреде-

лению ∂ϕ/∂t = ω, а ∂ϕ/∂x = −k. Однако передать сигнал с помощью

монохроматической волны, очевидно, нельзя из — за ее однородности в

пространстве и во времени (она должна существовать во все времена t

от −∞ до +∞ и на всей оси x от −∞ до +∞). Таких волн в природе,

конечно, нет: у всякого волнового процесса есть начало и конец, т. е.

313

реальный сигнал всегда имеет конечную ширину спектра частот и рас-

пространяется в общем случае со скоростью, не равной v

. Пусть теперь

мы каким-то образом изменяем амплитуду или фазу волны, чтобы мож-

но было передать информацию. Рассмотрим для определенности задачу с

такими начальными условиями: в начальный момент времени t = 0 вол-

на задана пространственным распределением u = Re[f(x) exp(−ik

x)],

причем f(x) изменяется медленно по сравнению с exp(−ik

x). Можно

ожидать, что волна будет распространяться как волна с постоянной ам-

плитудой u = Re{f(x) exp[i(ω

t − k

x)]}, т. е. со скоростью v = ω

(ср. с (13.1)). Однако в средах с дисперсией это не так. Действительно,

представим f(x) в виде интеграла Фурье

f(x) ∼

+∞

−∞

g(k)e

−ikx

dk , где g(k) ∼

∞

−∞

f(x)e

ikx

dx .

Тогда

u(x, 0) ∼ e

−ik

+∞

−∞

g(k)e

−ikx

dk ∼

+∞

−∞

g(k)e

−i(k+k

dk .

Заметим, что наш интеграл — это непрерывный набор волн постоянной

амплитуды, существующих на всей оси x от −∞ до +∞. Тогда для груп-

пы волн (волнового пакета)

u(x, t) ∼

+∞

−∞

g(k)e

i[ωt−(k+k

)x]

dk . (13.2)

Как мы знаем, в диспергирующей среде ω = ω(k). Медленность измене-

ния f(x) по сравнению с exp(−ik

x) означает, что g(k) отлично от нуля

только для k  k

,поэтому функцию ω(k) можно разложить в ряд и

ограничиться двумя членами разложения:

ω(k

+ k) = ω

dω



k . (13.3)

Подставляя (13.3) в (13.2), получаем

u(x, t) ∼ e

i(ω

t−k

+∞

−∞

g(k)e

−ik[x−(dω/dk)

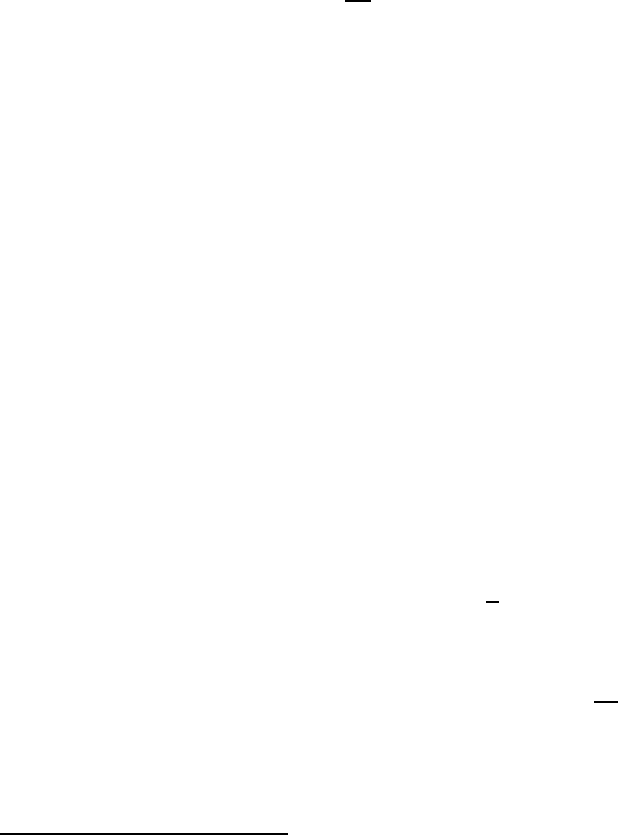
314

или

u(x, t) = f[x − (dω/dk)

t] e

i(ω

t−k

Если рассматривать f[x −(dω/dk)

t] как изменяющуюся амплитуду вол-

ны, фазовая скорость которой v

= ω

, т о изменение амплитуды рас-

пространяется с групповой скоростью.

гр

dω



k=k

Долгое время считалось, что на особенности распространения группы

волн первым в 1876 году обратил внимание Дж. Стокс. Правда, в кон-

спекте Л.И. Мандельштама (см. [1], стр. 420) было упоминание о более

ранних работах У.Р. Гамильтона. В небольшой заметке [6] М.Л. Левина,

замечательного физика и удивительного человека, показано сколь далеко

продвинулся У.Р. Гамильтон в понимании этого вопроса задолго до Сток-

са и Рэлея. Гамильтон анализировал “среду” в виде дискретной решетки

довольно общего вида с собственными волнами типа u ∼ cos(kx − st +

+ψ) [7]. Он интересовался вопросом что будет через большой промежуток

времени с возмущением, которое при t = 0 имело вид u(0) ∼ cos(kx + ψ)

и занимало ограниченную область решетки? Гамильтон получил следу-

ющий результат [7]: “ . . . введенные выше формулы сразу имеют ди-

намическое приложение и соответствуют распределению колебательного

движения через систему взаимно притягивающихся или отталкивающих-

ся точек; они приводят к тому замечательному результату, что скорость,

с которой такое коле ба ние распространяется в тех частях колеблющейся

среды, которые раннее были невозмущенными, в общем случае отлична

от скорости перехода некоторой данной фазы от данной частицы к другой

внутри той части среды, которая уже полностью возбуждена:

Скорость переноса фазы =

но

Скорость распространения колебательного движения =

. . . ”

Название статьи М.Л. Левина “Как свет побеждает т ьму . . . ” связано

с тем, что у У.Р. Гамильтон пишет о скорости, “с которой свет данного

цвета завоевывает темноту . . . ” [7]

Здесь уместно настоятельно порекомендовать читателю прочитать книгу [8]. Почему?

315

Учтем в разложении функции ω(k) в ряд еще одно слагаемое по срав-

нению с (13.3):

ω(k

+ k) = ω

dω



k +



Чтобы можно было пренебречь в показателе экспоненты в (13.2) допол-

нительной фазой (d

ω/dk

)

t/2), должно выполняться неравенство

[(d

ω/dk

)(k

t/2)]  1, которое можно переписать в виде

|(π/v

гр

)(dv

гр

/dλ)

∆|  1 .

Здесь введено расстояние ∆ = v

гр

t, на которое сместилась "амплитуда"за

время t, и использовано равенство k = 2π/λ, где λ — длина волны. Рас-

стояние ∆ — это тот характерный масштаб, на котором справедливо наше

рассмотрение; он тем больше, чем меньше (dv

гр

/dλ)

. Итак, групповая

скорость есть характеристика движения волнового пакета в диспергиру-

ющей среде, если пакет еще сохраняет свою форму и размеры, т. е. на

расстояниях порядка ∆. В некотором смысле пакет в этом случае подо-

бен частице в классической механике, а групповая скорость всего пакета

подобна скорости частицы.

Рассмотрим еще один способ введения понятия групповой скорости,

для чего проанализируем распространение сигнала с дискретным спек-

тром частот (рис. 13.1,а)

u = Re

i(ω

t−k

+ u

i(ω

t−k

+ u

i(ω

t−k

+ . . .

Представим такую суперпозицию монохроматических волн с ч астотами

, ω

. . . в виде

u = Re

F e

i(ω

t−k

, (13.4)

где

F = u

+ u

i[(ω

−ω

)t−(k

−k

)x]

+ u

i[(ω

−ω

)t−(k

−k

)x]

+ . . . . (13.5)

Функция F (x, t) называется комплексной огибающей высокочастотного

сигнала в пространстве и во времени [2]. Смысл этого названия легко

Ответ звучит в первых строках предисловия ко второму изданию книги.

“Мы предвидели притягательность этой книги, но все же не ожидали столь проника-

ющего ее воздействия на людей разных жизненных устоев. Вероятно, все мы тянемся

сопоставлять с вои свойства и судьбы с какими - либо “образцами” — предпочтительно

“типично необычными”. И это обогащает наши жизни новыми смыслами . . . ”

316

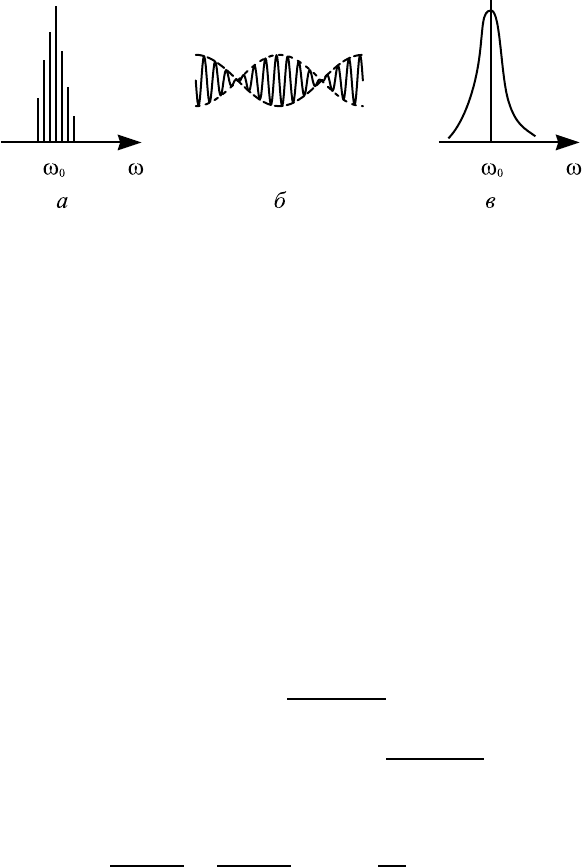
Рис. 13.1. Узкий дискретный спектр — все составляющие

близки к ω

(а); пакеты волн, ограниченные огибающей

модуля ции (2), которая переносит в отличие от высокоча-

стотного заполнения (1) всю информацию о сигнале (б) и

пример непрерывного спектра сигнала (в).

понять, если ввести F = A exp(iϕ). Тогда из (13.4) имеем квазигармони-

ческую волну u = A cos(ω

t − k

x + ϕ) (A —огибающая, (ω

t − k

x) —

высокочастотная фаза, ϕ — медленно изменяющаяся фаза). Если спектр

сигнала узкий (все спектральные составляющие сосредоточены около ω

то все разности типа ω

−ω

и k

−k

(n = 1 , 2 , . . . ) малы. Следователь-

но, в (13.4) функция F изменяется медленно со сравнению с exp[i(ω

t −

− k

x)]. Экспоненциальный множитель соответствует распространению

монохроматической волны с частотой ω

, которая называется несущей.

Перепишем формулу (13.5) в виде

F = u

+ u

exp



−i(k

− k

)



x −

(ω

− ω

− k



+ u

exp



−i(k

− k

)



x −

(ω

− ω

− k



+ . . . (13.6)

Для узкого спектра можно положить

− ω

− k

− ω

− k

= . . . =

= v

гр

(равенства выполняются тем точнее, чем уже спектр), и, следовательно,

F = u

+ u

exp[−i(k

− k

)(x − v

гр

t)] +

exp[−i(k

− k

)(x − v

гр

t)] + . . . = F (x −v

гр

t) . (13.7)

Сказанное выше позволяет определить групповую скорость как скорость

распространения огибающей сигнала (рис. 13.1,б). Если в дисперсионном

317

уравнении связь между ω и k линейная и однородная, то dω/dk = ω/k =

= v

и волновой пакет распространяется так же, как отдельная монохро-

матическая волна, — это отличительный признак среды без дисперсии.

Для сигнала с непрерывным спектром, занимающим узкий интервал

около некоторой фиксированной частоты ω = ω

(рис. 13.1,в), соотноше-

ние (13.7) остается в силе [2]. Конечно, и при таком подходе понятие

групповой скорости по-прежнему справедливо, пока пакет не исказился,

т. е. для сравнительно малых промежутков времени и для сигналов с

узким спектральным диапазоном.

Введем понятие групповой скорости теперь из более о бщих сообра-

жений для волны, которая квазигармонически плавно модулирована и по

амплитуде, и по частоте, т. е. имеет вид u(x, t) exp[iΨ(x, t)], где Ψ —

быстро осциллирующая фаза (помимо узкого пакета можно рассмотреть

широкий k-паке т, для которого изменения k имеют порядок самого k).

Мгновенные частоты и волновое число опреде ляются производными ф а-

зы по формулам

ω(x, t) =

∂Ψ

∂t

, k(x, t) = −

∂Ψ

∂x

(13.8)

и, очевидно, удовлетворяют уравнению

∂k

∂t

∂ω

∂x

= 0 . (13.9)

Если разложить Ψ в ряд около какой-либо точки (x

, t

), то ω и

k совпадут с лока льными частотой и волновым числом в традиционном

определении, когда характерный масштаб изменений ω и k велик по срав-

нению с 1/ω и 1/k. Предположим, что на пространственных интервалах,

много больших периода модуляции, но меньших характерного масштаба

ее изменений, локальная частота близка к частоте синусоидальной волны

с данным “локальным” значением k. Тогда ω и k связаны дисперсионным

уравнением ω = ω(k). Используя его в (13.9), получаем

∂k

∂t

∂ω

∂k

∂x

= 0 , или

∂k

∂t

+ v

гр

(k)

∂k

∂x

= 0 , (13.10)

где v

гр

(k) = ∂ω/∂k. Таким образом, можно дать еще одно важное для

понимания кинематики волнового движения определение: групповая ско-

рость v

гр

(k) есть скорость распространения возмущений волнового чис-

ла k. Уравнение (13.1) для k является гиперболическим нелинейным урав-

нением даже тогда, когда исходная задача линейная. Из этого уравнения

следует постоянство k вдоль кривых — характеристик на плоскости (x, t),

318

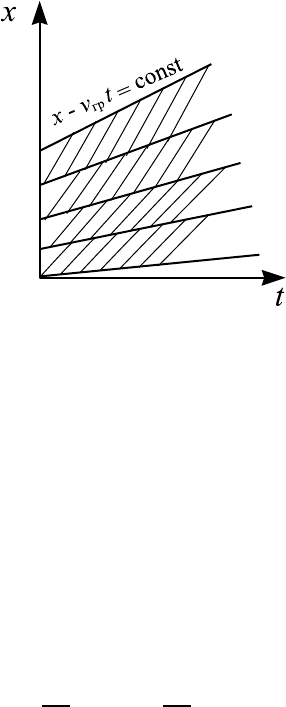
Рис. 13.2. Поведение группы волн на плоскости xt; вдоль

жирных прямых x − v

гр

t = const (λ = 2π/k = const); тра-

ектория гребней волн, возникающих из “ничего” и исчеза-

ющих на фронте, показаны тонкими линиями [3].

для которых dx/dt = v

гр

откуда, в свою очередь, вытекает, что и v

гр

= const, т. е. характеристики — это прямые, определяемые уравнением

x − v

гр

t = const (13.11)

(рис. 13.2).

Ясно, что вместо (13.10) можно пользоваться уравнением

∂ω

∂t

+ v

гр

(ω)

∂ω

∂x

= 0 , (13.12)

которое также нелинейно; о дисперсии, следовательно, можно говорить

как о "частотной нелинейности". Левая часть (13.12) есть dω/dt, взятая

вдоль линии dx/dt = v

гр

на плоскости (x , t), т. е. уравнение (13.12) озна-

чает, что вдоль указанной линии ω = const. Но тогда и v

гр

(ω) = const

вдоль характеристик t − x/v

гр

(ω) = ξ(ω), где ξ = const для данного ω.

Зависимость ξ(ω) определяется модуляцией частоты при x = 0; таким

образом, общее решение уравнения (13.12) имеет вид

ω = Ω[t − x/v

гр

(ω)] , (13.13)

где Ω — произвольная функция, обратная ξ(Ω). Решение (13.13) подробно

обсуждается в связи с теорией простых волн, поведение которых опре-

деляется тем, что каждая точка профиля простой волны д вижется со

319

Рис. 13.3. Распространение частотно-модул ированной вол-

ны. Схема сжатия и последующего расплывания пакета (а)

и соответствующая пространственно временная диаграмма

(б).

скоростью v(ω) — постоянной, но разной для разных ω. Поэтому мож-

но представить волну как совокупность независимых групп, движущихся

каждая со своей скоростью.

Очевидно, что в зависимости от модуляции частоты эти группы мо-

гут и расходиться, и сближаться, обгоняя друг друга и вновь расходясь.

Если построить характеристики на плоскости (x , t), то можно получить,

например, фокус — точку, в которой сходятся две ил и три группы, потом

эти группы опять разбегаются (рис. 13.3). При этом проявляется неод-

нозначность в решении (в потоке невзаимодействующих частиц). Здесь

очевидна аналогия и с поведением лучей в обычной геометрической опти-

ке (см гл. 17). В [4], например, показано, что эта аналогия не случайна,

и для диспергирующей среды естественно говорить о приближении про-

странственно - временной геометрической оптики.

Если заменить ω через v

k и использовать k = 2π/λ, то из определе-

ния v

гр

= ∂ω/∂k приходим к формуле Рэлея.

гр

= v

− λ

dλ

. (13.14)

Из соотношения (13.14) видно, что групповая скорость может быть как по-

ложительной и нулевой, так и отрицательной, как больше фазовой, так и

меньше. Простой способ определения v

гр

по кривой v

= v

(λ) был пред-

ложен еще Эренфестом. Этот способ легко понять из рис 13.4. Примерами

реальных волн, у которых v

гр

и v

противоположны по направлению, слу-

жат обратные электромагнитные волны или обратные пространственные

гармоники электромагнитной волны, которые распространяются в замед-

ляющих системах, используемых в СВЧ усилителях и генераторах типа

ламп с обратной волной (ЛОВ).

320

Рис. 13.4. К графическому определению v

гр

: а — v

гр

> 0;

б — v

гр

> 0 для λ = λ

и v

гр

< 0 для λ = λ

. Отрезок,

отсекаемый на оси ординат касательной к кривой v

(λ),

проведенной, например, в точке λ = λ

этой кривой, равен

−λ(∂v

/∂λ)

В лекциях [1], анализируя рисунки, подобные рис. 13.4, Л.И. Ман-

дельштам приводит следующие красивые и понятные образы — примеры.

“ . . . если кривая v

(λ) достаточно круто поднимается, т о групповая

скорость может обращаться в нуль, и сделаться отрицательной . . . При

отрицательной групповой скорости медленно меняющаяся амплитуда дви-

жется в сторону, противоположную направлению распространения волн,

составляющих группу.

Как представить себе это наглядно? Флеминг приводит следующий

пример: по плывущей барже вереницей бегут мальчики, спрыгивают с

носа в воду и взбираются затем на корму. Если мальчики будут бежать в

сторону, противоположную движению баржи, т о мы и получим картину

отрицательной групповой скорости (скорость баржи). Примером нулевой

групповой скорости может служить экскалатор: ступени (играющие роль

волн) движутся, а группа в целом, т.е. весь экскалатор стоит на месте”.

Мы не касались вопроса о скорости распространения короткого им-

пульса в диспергирующей среде. Изложение состояния можно найти, на-

пример, в обзоре [9]. Подчеркнем лишь, что для коро ткого импульса и

импульса с широким частотным спектром понятие групповой скорости

становится неопределенным: форма импульса сильно искажается по мере

его распространения.

Наконец, введем понятие скорости распространения энергии в среде :

V =

Средняя плотность потока энергии

Средняя плотность энергии

Как показано М.А. Леонтовичем, в том случае, когда в среде отсутствует