Ткаченко В.Н. Электрохимическая защита трубопроводных сетей
Подождите немного. Документ загружается.

111
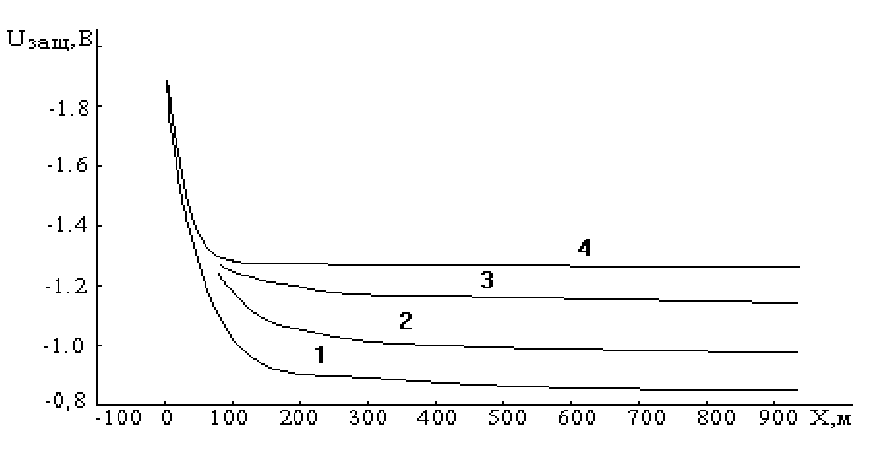
Рис.5.6. Распределение защитного потенциала вдоль трубопровода
при различных поляризационных характеристиках. Номера у кривых
соответствуют данным в колонках Р
1
...Р
4
табл.5.5.
5.6.2. Последействие катодной поляризации
Поскольку по мере накопления катодных осадков и увеличения поля-
ризационного сопротивления поляризационный потенциал U
пол
во вре-
мени медленно возрастает, достигая своего предела через сотни часов, то
снижение поляризационного потенциала - при выключении тока поляри-
зации - не может быть мгновенным и также может длиться много часов.
Именно этот эффект последействия используют при измерении поляри-
зационной составляющей защитного потенциала
Δ
U
пол
, о чем сказано
выше.
Но известны успешные примеры использования эффекта последей-
ствия не только при измерениях потенциала, но и непосредственно для
увеличения эффективности катодной защиты. Действительно, если ме-
таллическое сооружение какое-то время после отключения тока поляри-
зации “помнит” свой защитный потенциал, то было бы выгодно приме-
112
нять катодную защиту в прерывистом режиме, чередуя включение ка-
тодной защиты с ее выключением.
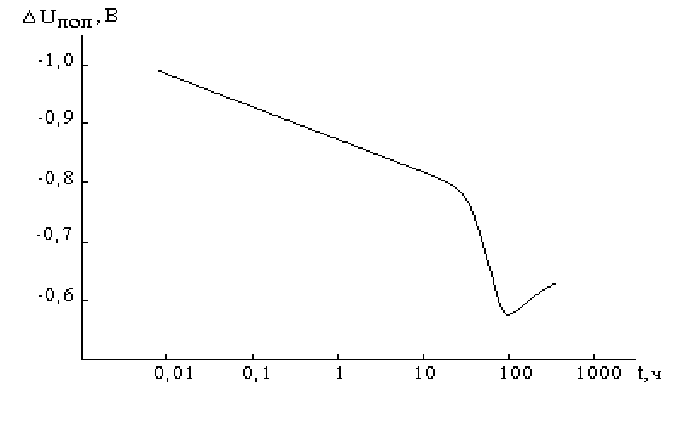
Рис.5.7. Изменение потенциала стали после отключения ка-
тодного тока при продолжительности поляризации 500 ч и
плотности тока 200 мА/м
2
.
На рис.5.7 показана характерная кривая снижения электродного по-
тенциала стали после отключения катодного тока [1].
Судя по характеру кривой, катодную защиту - благодаря эффекту по-
следействия - можно было бы безболезненно отключить на 10 и более ча-
сов, после чего включить ее снова и, вероятно, на такой же срок.
Возврат металла к своему стационарному состоянию продолжается
очень долго и может превышать сотни часов.
Эффект последействия ярко проявляется в жидких средах, т.е. в мор-
ской и речной воде, и используется при защите таких сооружений как
корпуса судов. Но, к сожалению, этот эффект незначителен для подзем-
ных трубопроводов. Как отмечено в практике, при отключении катодной
защиты на трубопроводе вместо эффекта последействия могут возник-
нуть коррозионные макропары.
Действительно, вследствие того, что процесс располяризации или
“разряда” замедлен, область трубопровода вблизи анодного заземлителя,
как более электроотрицательная часть трубопровода, будет какое-то вре-
мя работать анодом.
113
Такая гальваническая макропара может функционировать несколько
часов, принося ощутимый и порой неожиданный ущерб. Не редки случаи,
когда отмечалась язвенная коррозия на трубопроводах, казалось бы за-
щищенных надежно. Причина этому - периодические перерывы в элек-
троснабжении катодных станций.
114
Глава 6. Решение сетевой задачи электрохимической
защиты
6.1. Исходная система уравнений
6.1.1. Сетевая задача электрохимической защиты
Под сетевой задачей будем понимать задачу расчета распределения
тока и потенциала в трубопроводной сети произвольной конфигурации в
поле внешних (блуждающих и защитных) и собственных (гальваниче-
ских) токов.
Предлагаемый ниже метод решения сетевой задачи пригоден также
для расчета распределения тока и потенциала в рельсовой сети электро-
транспорта, в металлических оболочках кабельных линий, вдоль стерж-
ней сложных контуров заземления, в арматурной сетке железобетонной
конструкции, по обсадной колонне скважины и на других подобных ме-
таллических сооружениях.
Перечисленные задачи образуют новую, ранее не рассмотренную в
теории группу задач для системы электрических проводников с утечкой,
отличительная особенность которой:
- произвольная конфигурация сети проводников;
- электрическая и гальваническая неоднородность участков;
- взаимовлияние полей токов проводников в земле.
В зависимости от постановки сетевой задачи искомыми при решении
могут быть:
1) потенциал (потенциал трубопровода и потенциал земли, разность
потенциалов сооружение-земля, градиент потенциала при заданных то-
ках источников и известном сопротивлении цепей);
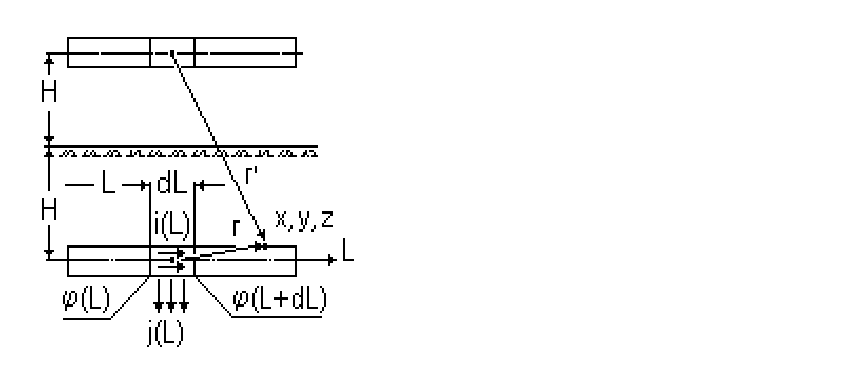
115
2) ток (ток источников, вызывающих заданный потенциал при за-
данном сопротивлении цепей, количество источников и их оптимальное
размещение в трубопроводной сети);
3) сопротивление (удельное сопротивление изоляции, поляризацион-
ное сопротивление, сопротивление дренажной перемычки при заданном
токе и потенциале).
Решения всех трех задач в конечном счете построены на одном фун-
даменте - законе Ома для электрического проводника с утечкой конечной
длины.
6.1.2. Основные уравнения и формулы
Пусть участок подземного трубопровода отсечен от сети и находится
в поле каких-либо внешних или собственных токов. Направим вдоль оси
трубопровода криволинейную координатную ось 0L и рассмотрим вблизи
точки L элементарный участок длиной
Δ
L (рис.6.1).
Рис.6.1.Расчетная схема для
вывода основных уравнений
для тока и потенциала трубо-
провода, где r′ - расстояние от
элементарного участка зер-
кального отображения трубо-
провода до исследуемой точки
у поверхности реального тру-
бопровода
.
Если ϕ
т
( L ) и ϕ
т
( L+
Δ
L) - потенциалы трубопровода на границах
элементарного участка, то по закону Ома для продольного тока будем
иметь
i(L) = ( ϕ
т
(L+
Δ
L)
−
ϕ
т
(L) ) / (R
пр
Δ
L) ,
116
где i(L) - среднее значение продольного тока трубопровода на элемен-
тарном участке
Δ
L; R
пр
- удельное продольное сопротивление трубопро-
вода, Ом/м.
В дифференциальной форме это уравнение имеет вид
i(L) =
−
1 / R
пр
.
dϕ
т
(L) / dL, (6.1)
где знак “−“ утверждает, что принятому направлению тока ( i > 0 ) соот-
ветствует противоположное направление градиента потенциала (d
ϕ
т
< 0).
Но ток на элементарном участке dL не постоянен. Изменение про-
дольного тока di(L) здесь определяет ток утечки трубопровода, т.е.
j(L) =
−
di(L) / dL , (6.2)
где j(L) - линейная плотность тока утечки трубопровода, А/м.
При этом принято, что ток утечки положителен, если он направле-
нии из трубы в землю, и отрицателен, если он натекает из земли на тру-
бопровод. Тогда в соответствии с принятым направлением тока при j > 0
должно быть di < 0, т.е. уменьшение продольного тока в положительном
направлении координатной оси, что и отмечено знаком “−“.
Формулы (6.1) и (6.2) приводят к одному из основных уравнений,
связывающих две неизвестные j и ϕ
т
j(L) = 1/ R
пр
d
2
ϕ
т
(L) / dL
2
. (6.3)
Другое уравнение для тех же неизвестных имеет вид
R
из
j(L) = ϕ
т
(L)
−
ϕ
зем
(L)
−
ϕ
ст
(L), (6.4)
где R
из
- удельное сопротивление изоляции трубопровода, Ом
.
м; ϕ
зем
- по-
тенциал земли у стенки трубопровода; ϕ
ст
- стационарный потенциал ме-
талла трубы относительно выбранного электрода сравнения.
Рассмотрим составляющие уравнения (6.4) подробнее.
Левую часть уравнения можно интерпретировать как напряжение на
изоляции трубопровода, т.е.

117
Δ
U = R
из
j (6.5)
или как смещение потенциала на поверхности трубы, вызванное токами
утечки трубопровода.
Правая часть уравнения (6.4) есть выражение этого же напряжения
Δ
U, но представленного как разность потенциалов трубы (ϕ
т
) и бли-
жайшей точки земли (
ϕ
зем
) с учетом электрохимической неэквипотенци-
альности металла трубы (ϕ
ст
).
Стационарный потенциал
Условимся различать стационарный потенциал металла ϕ
ст
и стацио-
нарный потенциал трубопровода U
ст
. Оба они прежде всего предполага-
ют, что при их измерении отсутствуют внешние токи. Но если U
ст
есть
обычным способом измеряемая разность потенциалов труба-земля, то ϕ
ст
есть разность потенциалов между обособленным “куском” трубы и зем-
лей, т.е. ϕ
ст
- электрохимический потенциал некоего обособленного ме-
таллического образца-электрода из материала трубопровода в данных
грунтовых условиях, измеренный относительно определенного электрода
сравнения. Часто ϕ
ст
называют потенциалом коррозии.
При решении задач с коррозионными гальванопарами следует поль-
зоваться понятием ϕ
ст
, а при решении только задач электрохимической
защиты можно полагать, что ϕ
ст
= U
ст
.
Потенциал земли
В правую часть уравнения (6.4) входит еще одна компонента - потен-
циал земли ϕ
зем.
. Его следует представить двумя составляющими
ϕ
зем
= ϕ
з.т
+
ϕ
з
,
(6.6)
где ϕ
з.т
- потенциал земли поля токов данного трубопровода; ϕ
з
- потенци-
ал земли, вызываемый токами внешних источников ( рельсовыми линия-
ми электротранспорта, анодными заземлителями установок ЭХЗ и т.д.).
Расчет потенциала земли (ϕ
з
)
базируется на известных законах, кото-
рые отображены в нижепредставленых расчетных формулах.
118
а) Потенциал земли в поле точечного источника тока
Потенциал в поле точечного источника тока (в идеальном случае - это
уединенный сферический заземлитель, подключенный к “+” источника
тока), находящегося в безграничной проводящей среде, вычисляется по
формуле
ϕ
з
= Iρ / (4πr) , (6.7)
где ϕ
з
- потенциал поля тока в исследуемой точке земли; I - ток точечного
источника; r - расстояние от источника до исследуемой точки земли;
ρ - удельное электрическое сопротивление земли.
Для источника, находящегося в земле на конечной глубине, формула
имеет вид
ϕ
з
= Iρ / (4π) (1 / r + 1 / r’) , (6.8)
где r’ - расстояние от зеркального (относительно дневной поверхности)
отображения источника до исследуемой точки.
В частном случае, когда точечный источник находится на поверхно-
сти земли (r = r’), имеем
ϕ
з
= Iρ / (2πr) . (6.9)
Реальный заземлитель может быть заменен точечным заземлителем
без заметной ошибки для исследуемой точки земли, если для радиальной
координаты этой точки справедливо r > 2 L
а
, где L
а
- максимальный раз-
мер заземлителя.
б) Потенциал земли в поле протяженного заземлителя
Если размеры заземлителя велики относительно расстояния до иссле-
дуемой точки, то его делят на отрезки, каждый из которых затем заме-
няют точечным источником тока. Тогда, если I - общий ток заземлителя,
L
а
- его протяженность, то j = I / L
а
- линейная плотность тока заземлите-
ля. Представляя линейный источник совокупностью точечных интенсив-
ностью jdL и допуская j = const, получим
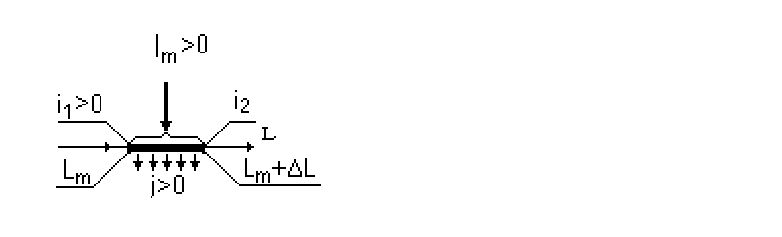
119
ϕρπ
з
0
L
(4 ) (1 / + 1 / ) ,=
′
∫
jr
/
rdL
ξ
()
4 jGxyzd
L
(6.10)
где r - расстояние от текущей точки на заземлителе до фиксированной
точки в земле; r’ - то же для зеркального отражения электрода (см.
рис.6.1).
в) Потенциал земли в поле трубопровода
Потенциал земли, вызванный токами утечки трубопровода, вычисля-
ется по формуле аналогичной (6.10), но с учетом того, что величина
плотности тока зависит от продольной координаты
ϕρπξξ
з .т
=
∫
/( ) ( ) ( , , , ) ;
(6.11)
G(
ξ
,x,y,z) = 1 / r (
ξ
,x,y,z) + 1 / r‘(
ξ
,x,y,z) ,
где r - расстояние между текущей точкой
ξ
на оси трубопровода и фикси-
рованной точкой x,y,z на его поверхности; r’ - то же самое, но от зеркаль-
ного отображения.
6.1.3. Граничные условия для участка сети
а) В точке подключения сосредоточенной токовой нагрузки
Рис.6.2. Расчетная схема
Пусть к точке L= L
m
обособленного участка сети приложена сосредо-
точенная токовая нагрузка I
m
, например, подключена катодная станция.
Рассредоточим нагрузку I
m
вдоль элементарного участка
Δ
L и в соответ-
120
ствии с принятыми на рис.6.2 направлениями токов, запишем первый за-
кон Кирхгофа для малого отрезка
Δ
L в окрестности точки L
m
:
i
1
− i
2
+ I
m
− j
Δ
L = 0 (6.12)
или
j = − ( i
2
− i
1
) /
Δ
L + I
m
/
Δ
L . (6.13)
Выполняя предельный переход, получим дифференциальное уравне-
ние для трубопровода с сосредоточенными нагрузками в точках m
j(L ) =
−
di(L) / dL + δ(L
m
,L) I
m
или
j(L) = (1 / R
пр
) d
2
ϕ
т
(L) / dL
2
+ δ(L
m
,L) I
m
(6.14)
где δ(L
m
,L)- дельта-функция Дирака, использующаяся как символ нали-
чия в точке L
m
сосредоточенного источника. Ее свойства в рассматривае-
мой ситуации:
δ(L
m
,L) = 0 при L
≠
L
m
;
δ(L
m
,L) I
m
= J
m
при L = L
m
,
где J
m
= I
m
/
Δ
L
m
- плотность тока внешней нагрузки в пределах элемен-
тарного участка
Δ
L
m
. В реальных условиях ток внешней нагрузки не мо-
жет быть приложен к физической точке и поэтому величина J
m
всегда ко-
нечна.
Наличие сосредоточенной нагрузки изменит вид дифференциального
уравнения (6.1), которое теперь следует различать для двух участков: до
точки подключения нагрузки и после нее:
⎧ −1 / R
пр
d
ϕ
т
(L) / dL при L
<
L
m
i(L) =
⎨
(6.15)
⎩ −1 / R
пр
d
ϕ
т
(L) / dL + I
m
при L
≥
L
m
