Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


§2,
Застосування операційного числення
451
\2х" - х + 9х - у* - у - 3у = 0,
4-57. і . , . ,
[2х + х +7х->' + у -5_у = 0,
х(0) = х'(0) = 1, Х0) = /(0) = 0.
Ї
х'
- у' - 2х + 2у =
1
- 2(,
х + 2у + х = 0,
х(0) = х'(0) = Я0) = 0.
х'
= -у-2,
4.59. • у'= -х-2,
/ = -х-у, х(0) = -1, Х0) = 0, г(0) = 1.
4.60.
4.61.
X =У + 2,
у'
= Зх + 2 ,
г' = 3х + у, х(0) = 0, у(0) = 2(0) = \.
х'
= 2х - у + 2,
у'
= Х + 2,
2 = -Зх + у-2г, х(0) = у(0) = \, г(0) = 0.

ГЛАВА
5. ТИПОВІ РОЗРАХУНКОВІ ЗАВДАННЯ
§1.
Індивідуальне завдання
1.
Диференціальні рівняння
Задача
1. [ гл. І, § 1,
приклади
З -14 ]
Розв'язати задані диференціальні рівняння першого порядку.
Варіанти завдань
1.
а)
(\+х
2
)сіу
+ х(\ +
у
2
)ах
= 0; б) / = ^ + зіп^;
в
) У+УЩх
=
созх
г)
сіу =
(у
2
е
х
-у)сіх;
д) (\0ху-&у
+ \)сіх + (5х
2
-8х +
3)ф-
= 0.
2.
а)
е
х+ь
сіу
= хах ;
в) у'-^
= х
2
;
х
д) Зх
2
е
у
ах
+
(х\"-1)0у
= 0.
3.
а) / =
(2х-1)сі§
у;
в)
(х
2
+
1)/
+ 4ху
= 3;
х
+ у
б)
/=
х-у
г)
ху'
+
у = у
2
\пх ;
б)
у - ху'
= —і--;
соз
г)
у'
+
у = хі[у ;
,2.2
2*
д)
Зх
+ —
соз
І
У У )
2х
2х
сіх
соз
—сіу
= 0 .
У
У
4.
В
)
Л^ах
+
-^-аУ
= 0;
б) (х-у)ах+(х+у)Оу
= 0;
г) /+2>>
=
.у
2
е*;
соз
х соз у
в) {\-х)(у'+у)
= е-
х
;
д) (Зх
2
+4\;
2
)Л:+(8х>' + Є'
>
')^
= 0.
5.а) (\+е
х
)уау-е>сІх=0;
б) (>>
2
-2ху)йх+х
2
й(у
= 0
в) ху'-2у
= 2х
4
; г) у-'= у
4
созх
+
.уІ§х
;
Д)
гх-і-^-"
1
х
,
<&-
2.У--
ф
= 0.
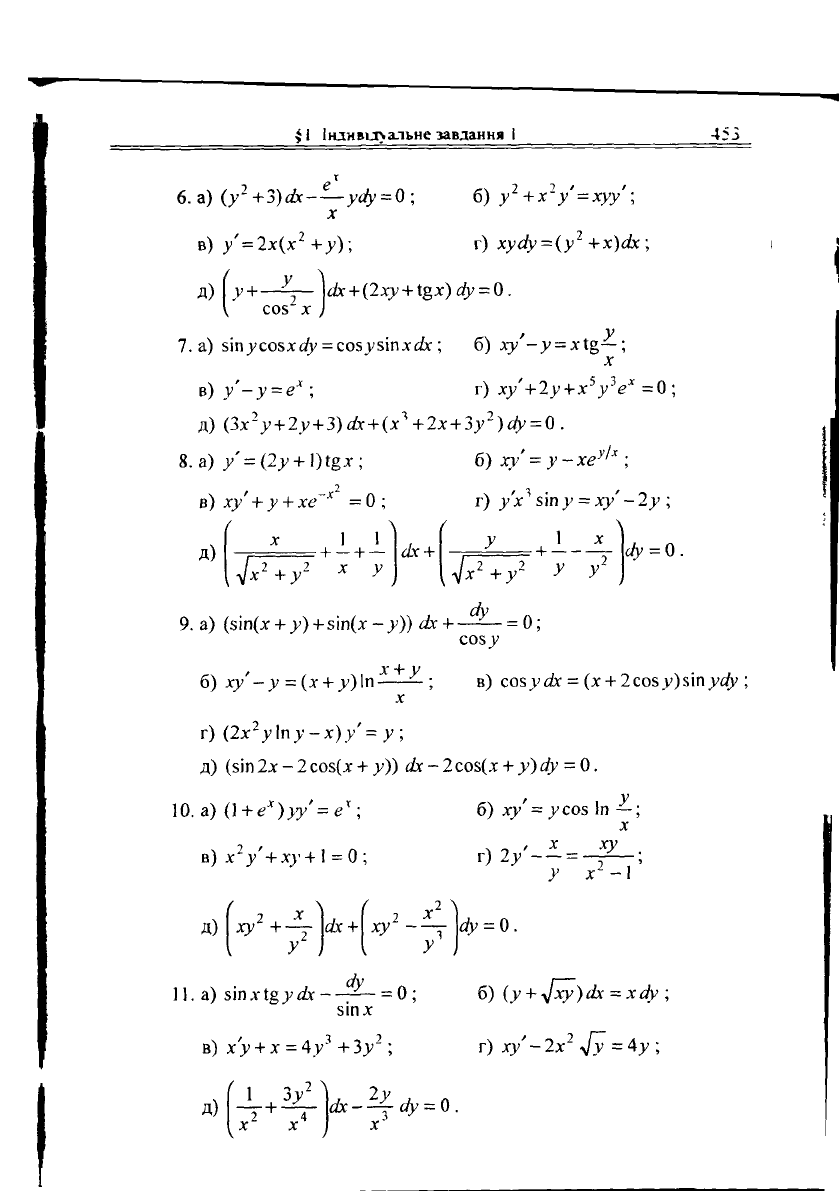
$1
1ндиаід>альне завдання
І
453
6. а) (у
2
+3)сіс ус/у = 0 ; б) у
2
+х
2
у' = хуу';
х
в) / = 2х(х
2
+у)\ г) хусіу = (у
2
+х)ах;
д) \у+
У
\ах + (2ху+Щх)ау = 0.
\ соз х )
7.
а) зіпусозхс/у ^озузіпхо^ ; б) ху -у = хі&—;
х
в)у'-у = е
х
; г) ху'+2у +
х
5
у
3
е
х
=0;
д) (Зх
2
у + 2і> + 3)ах + (х
3
+2х + 3.у
2
)а!у = 0.
8. а) / = (2 .у +1)Щх; б) ху' =
у-хе
у/х
;
в) ху' + у + хе
х
= 0;
Д)
х 1 1 .
г
+ — + — ах +
[УІХ
2
+У
2
Х
У) \^
2
+
у
2
У У
2
]
г)
у'х в'ту = ху'-2у;
У
1 х
:
+
ау = 0.
ау
9. а) (зіп(х + у) +
5Іп(х
- у)) сіх
н
= 0;
соз у
г х + у
б) ху -у = (х + у)\п —; в) соз>>ах = (х + 2со5>>)зіп.уй[у;
х
г) (2х
2
у\пу-х)у'= у;
д) (зіп 2х - 2 соз(х + у)) сіх - 2 соз(х + у) сіу = 0.
10.
а) (1 +і?
дг
)>у'= е
г
; б) ху' =
.у
соз Іп —;
в) х
2
у' + ху +
1
= 0 :
л т '
х
Х
У •
У X
і
Д)
2 X
XV
2
+-Т
У І
сіх
+
ху
2
-
і
т
|^ = о.
11.
а) зіпхі§уах= 0 ; б) (у + ^ху)ах = хау :
зіпх
в) х'у + х = 4 у
3
+ Зу
2
; г) ху' - 2х
2
>[у =4у ;
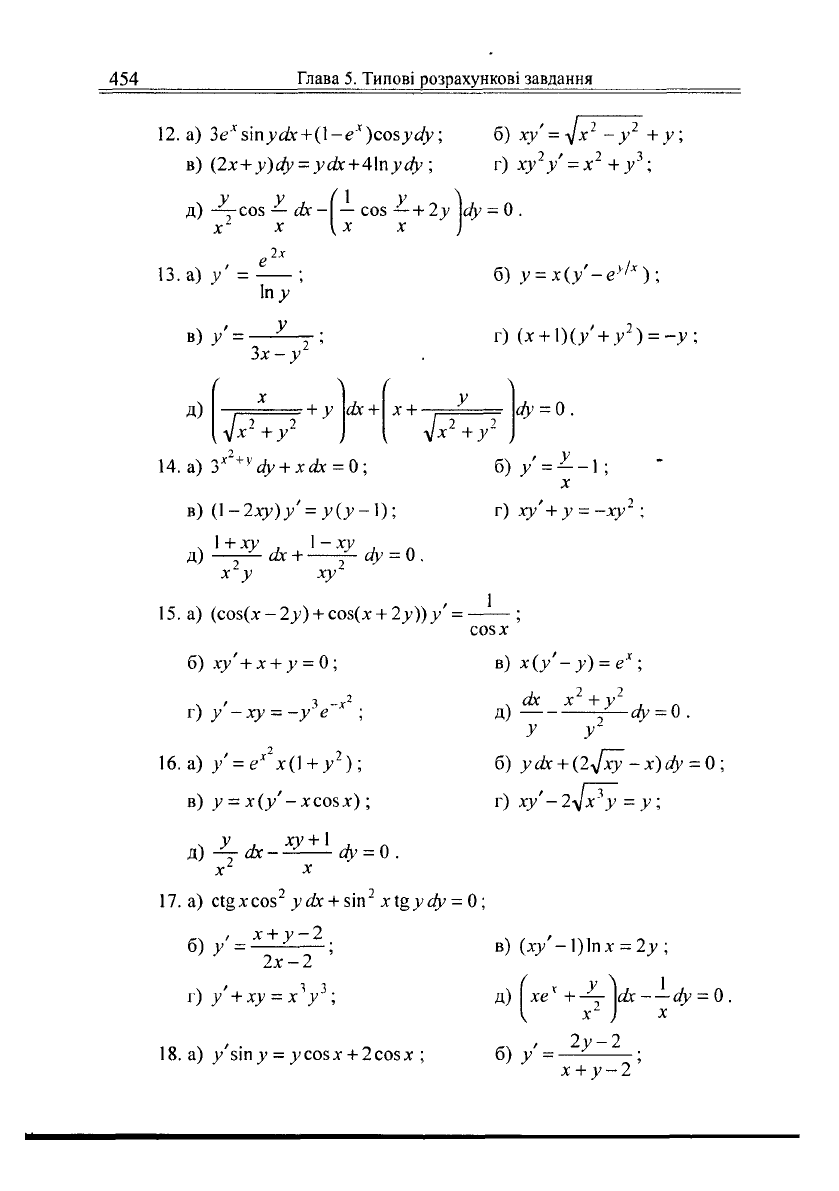
454
Глава 5. Типові розрахункові завдання
12.
а) Зе
х
$тусіх + (\-е
х
)со%усіу; б) ху' = ^х
2
- у
2
+у;
усіх + 4\пу<
П
У
-
— СОЗ —
\Х
X
в) {2х + у)
сіу
- усіх+ 4\п у Оу ; г) ху
2
у' = х
2
+ у
3
;
д)
-^г-СОЗ
—
ДХ
•
X
X
-
+ 2у
13.
а) / =
в) / =
•
1п
у
У
Зх-у
<
^ (
д)
•\]х
2
г
+
у
+
У
сіх
+
сіу = 0.
б) у =
х(у'-е
у/х
);
г) (х +
1)(/
+ .у
2
) = -у ;
д>>
= 0.
х +у~
14.
а) 3
х
+
у
д> + хдх = 0;
в) (]-2ху)у' =
у(у-\)\
д^Л
+
Ь^д^о.
х~
у-
ху
15.
а) (со$(х-2_у) +
со5(х
+ 2.у))>>':
б) ху'+ х + у = 0;
т) у - ху - -у е ;
16.
а) /^хО + у
2
);
в) у = х(у'- хсозх);
X
г) ху'+у = -ху
2
.
СОЗХ
в) х(у'-у) = е
х
;
сіх х
2
+у
2
Д)
у—
сіу = 0 .
У
У
б) усіх +
(2у[ху-х)Д>
= 0:
г) ху'-2у[х
3
у - у;
ЇЇ^сіх-
ху+
1
д>
= 0 .
х" *
17.
а) сі§хсоз
2
_удх + зіп
2
хЩусіу - 0;
,_
х + у-2_
б) /
2х-2
г) /
+
ху = хУ;
в) (х>>'-1)1пх - 2у;
>
» 1
Д)
хе" +
У_
.2
18.
а) у'зіпу - усовх + 2созх ;
б) /:
X
2у-2
сіх сіу = 0.
X
х+у-2'
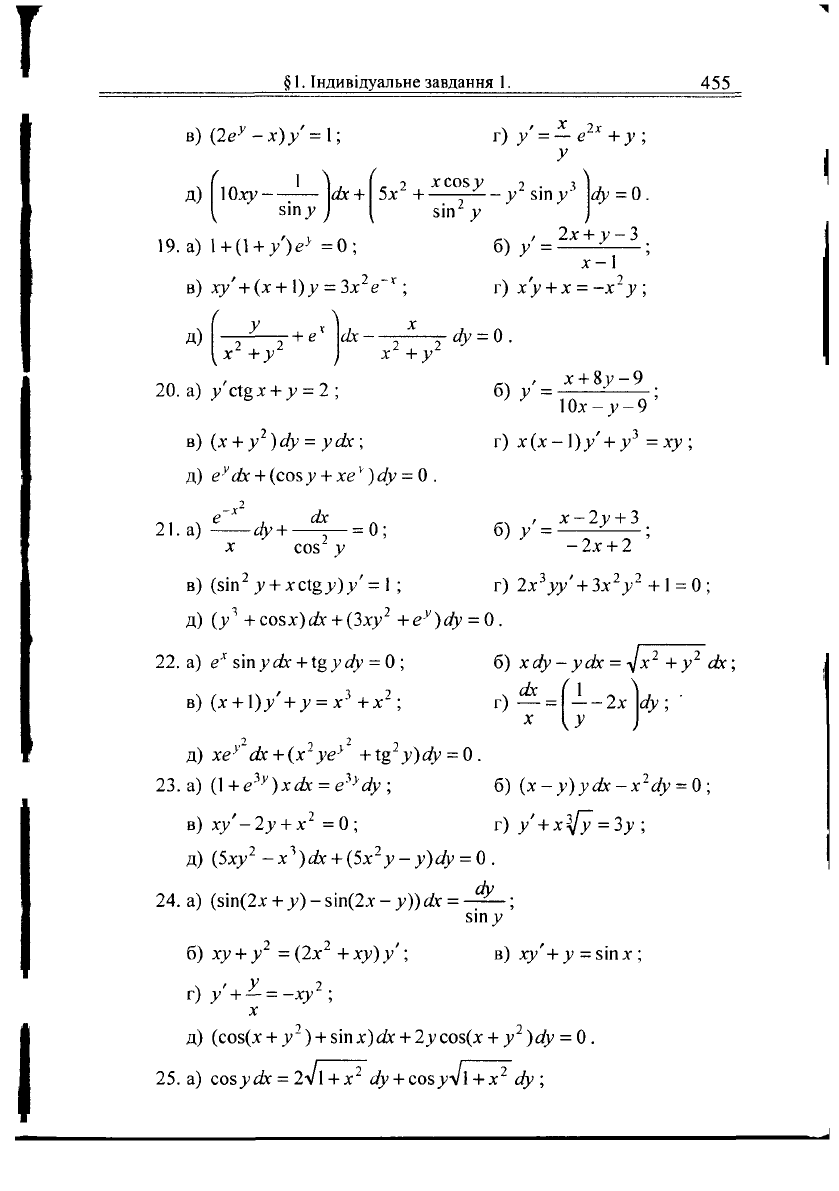
§
1,
Індивідуальне завдання 1.
455
в
д)
19.
а)
в)
а,
20.
^
в'
21.
а)
в'
X
22.
а
в^
д)
23.
а;
в}
д)
24.
а)
б)
г)
д)
25.
^
(2е
у
-х)у'=\;
\
'
х
2х
г) у =— є + у ;
У
,
2 ХСО&у
2
•
3
) ,
5х + т-^-у $ту ау=0.
зіп у
_2х + у-3
х-\
;
ху' + (х + 1)у = Зх
2
е~
х
; г) х'у + х = -х
2
у ;
Юху- —
сіх +
51ПІ>
)
1 + 0 + /)^ =0;
б) /
=
У
[*
2
+У
2
сіх-
2
2
X
+у
ау = 0.
х + &у-9
б) /
=
\0х-у-9
г) х(х-1)/ +у
3
=ху;
_
лг-2_у + 3 .
-2х + 2 '
г) 2х
і
уу' + 3х
2
у
2
+1 = 0;
/сі§х + у = 2 ;
(х + у
2
) сіу = усіх;
е
у
сіх+ (со$у + хе
]
')сіу = 0 .
е'
х
, сіх
п
,
сіу + — = 0; б) у
х соз у
(зіп
2
у + хс\%у)у' =
1
;
(у
3
+ созх)ах + (Зх>>
2
+е
у
)сіу = 0.
е
х
зіп у сіх +1§ у сіу = 0 ;
(х +
1)/
+у = X
І
+х
2
;
хе
у
сіх + (х уе
у
+І£-у)сіу = 0 .
(
\+е
3у
)хсіх =
е
3у
сіу
; б) (х-і')_у<ах-х
2
й(у = 0;
ху'-2у + х
2
= 0 ; г) у'+ хі[у =3у ;
(5ху
2
-х
3
)сіх + (5х
2
у-у)сіу = 0.
сіу
(зіп(2х + у)- зіп(2х - у)) сіх = ——;
зіпу
б) хсіу-усіх = -\х
2
+ У
2
сіх;
сіу, •
сіх (\ ^
X
--2х
ху + у
2
=(2х
2
+ху)у';
в) ху'+ у = зіп х ;
'
У 2
У +~ = -ху ;
X
(соз(х + _у") + зіпх)ах + 2усоз(х + у
2
) сіу = 0.
соз усіх =
2Л/І+Х
2
сіу +
со$у4\
+х
2
^/у ;
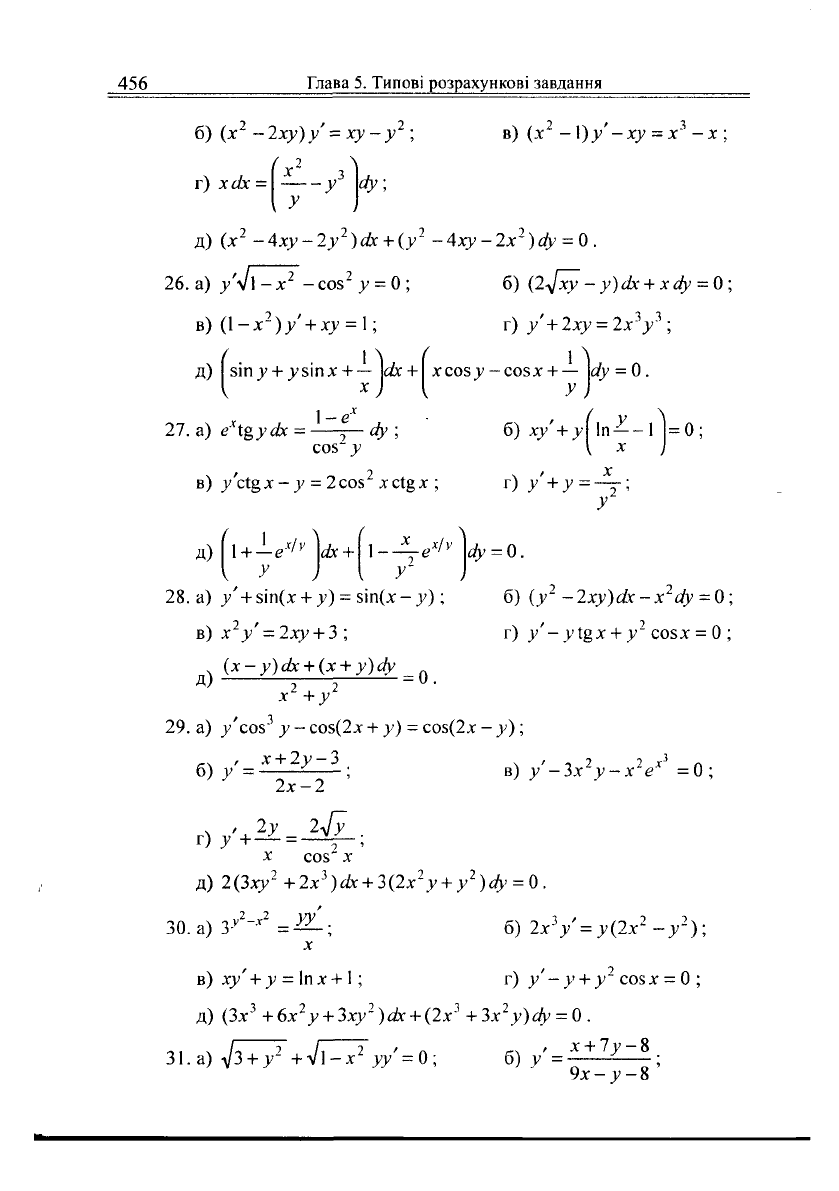
456
Глава 5. Типові розрахункові завдання
б) (х
2
-2ху)у' = ху - у
2
; в) (х
2
-1)у'-ху = х
3
-х ;
г) хах =
У
ау;
д) (х
2
-4ху-2>>
2
)ах + (.у
2
-4ху-2х
2
)ау = 0 .
26.
а)
у'4\-х
2
- соз
2
у = 0 ;
в) (1 -х
2
)
у'
+ ху = 1;
б) (2л[ху - у)ах + хау = 0 ;
г) у' + 2ху = 2х
3
у
3
;
Д)
ЗІП у + у8ІПХ + -
1 ї
ах + ХС05у-С05Х+- о> = 0.
27.
а) е
х
\%,уах- ^—оу ;
соз"
у
V
7
;
б) ху' + у| 1п^-1 |=0;
в) у'ст.§х- у = 2соз
2
хсІ§х ; г)у' +
у=——;
У
д) І \ + -е
х/у
\ах +
і \
Х
,,
Х
/У
оу = 0.
28.
а) у' + зіп(х + у) = зіп(х-у); б) (у
2
- 2ху)ах - х
2
ау = 0;
в) х
2
у'
—
2ху + 3 ;
(х-у)ох + (х + >')а> _
р
х
2
+ у
2
г) у - у (.§х + у" созх = 0 :
29.
а) у'соз' у - соз(2х + у) = соз(2х - у);
, х+2у-3,
6)У
=-2-х~Г>
г) / + ^
=
-Ь£;
* соз" х
д) 2(3ху
2
+2х
3
)ох + 3(2х
2
у + у
2
)ау = 0.
в) у'-3х
2
у-х
2
е* =0;
ЗО.
а) З
у
2
-"
2
=
УУ
X
б) 2х
3
у'= у(2х
2
- у
2
);
г) у - у + У соз х = 0 ;
в) ху' + у = 1пх +1;
д) (Зх
3
+ 6х
2
у + Зху
2
)ах + (2х
3
+ Зх
2
у)сіу = 0 .
31.а)
,/зТ7 +
ЛП^/ = 0; б) У=1
+
7У
~1;
9х - у - 8

§
1.
Індивідуальне завдання 1.
457
х
ХУ
,2
в) у' + 2ху = хе
х
; г) у' = Хл[у +
д) ху
2
ах + у(х
2
+у
2
)с1у = 0 .
Задача 2. [ гл. 1, § І, приклади 18-20]
Розв'язати задану геометричну задачу.
Варіанти завдань
У варіантах 1-3 знайти рівняння кривої, яка проходить через точку
А(х
0
,у
0
), якщо довжина відрізка півосі абсцис, що відтинається її дотич-
ною,
дорівнює квадрату абсциси точки дотику.
1 А
2.
Л(1; -2). 3. 3).
1.
А
; -1
2
У варіантах 4-6 знайти рівняння кривої, що проходить через точку
А(х
0
,у
0
), якщо відомо, що кутовий коефіцієнт дотичної в кожній її точці в
п разів більше кутового коефіцієнта прямої, яка з'єднує цю точку з почат-
ком координат.
4.
А(\; 4), п = 6.
5.
Л(3; -1), л = 8.
6. Л(-8; -2), л = 3 .
У варіантах 7-9 знайти лінію, яка проходить через точку А
0
(х
0
, у
0
)
і має таку властивість: в кожній точці А(х,у) нормальний вектор АВ з кін-
цевою точкою на осі Оу має довжину а і утворює гострий кут з додатним
напрямком осі Оу .
7.
А
0
(\5;
\),а = 25.
8. Л
0
(12; 2), а = 20.
9. А
0
(3; 5), а = 5.
У варіантах 10-12 знайти рівняння кривої, яка проходить через точку
А(х
0
,у
0
),
якщо її піддотична вдвічі більше абсциси точки дотику.
10.
А(\; 2). 11. А(-\; 3). 12. Л(4; -1).
У варіантах 13-15 знайти лінію, яка проходить через точку А(х
0
,у
0
),
якщо відрізок кожної її дотичної, що міститься між осями координат, ді-
литься в точці дотику в співвідношенні а:Ь (відраховуючи від осі Оу ).
13.
А{2; 2),а:Ь = \\\.
14.
Л(1; 2),а:Ь = 2:\.
15.
А(1; -\),а:Ь = \:3.

458
Глава 5. Типові розрахункові завдання
У варіантах 16
—
18 записати рівняння кривої, що проходить через
точку А(х
0
,у
0
) і має таку властивість: довжина перпендикуляра, який опу-
шений з початку координат на дотичну до кривої, дорівнює абсцисі точки
дотику.
16.
А(5; 3). 17. Л(-1;4). 18. Л(0; -5).
У варіантах 19-21 знайти рівняння кривої, яка проходить через по-
чаток координат, якщо середина відрізка її нормалі від довільної точки кри-
вої до осі Ох лежить на параболі ау
2
- 2рх .
19.
а = 2, р = 4. 20. а = 1, р =-. 21.а = 3, р = 2.
4
У варіантах 22 — 24 записати рівняння кривої, яка проходить через
точку А(х
0
,у
0
), якщо відомо, що відрізок, який відтинає дотична в довіль-
ній точці кривої на осі Оу , дорівнює півсумі координат точки дотику.
22.
Л(10;-1). 23. /4(12;-2). 24. Л(1;-9).
У варіантах 25 - 27 знайти лінію, яка проходить через точку
А
0
(х
0
,у
0
)
і мас таку властивість: в кожній її точці А(х,у) дотичний вектор
АВ з кінцевою точкою на осі Оу має проекцію на вісь Оу , що дорівнює а.
25.
Л
0
(1; 4), д = 2 .
26.
Л
0
(-1;
5), а = \ .
21.
Л
0
(1; 6), а = 3 .
У варіантах 28 - 29 знайти рівняння кривої, що проходить через точ-
ку А(х
0
,у
0
), якщо площа криволінійної трапеції, яка обмежена дугою цієї
кривої, в п разів більше довжини відповідної дуги.
28.
ДО; 2), п = 2.
29. А(0; -1), п = 4.
Уваріантах ЗО-31 знайти лінію, яка проходить через точку А(х
0
,у
0
)
і мас таку властивість: відрізок дотичної між точкою дотику і віссю ординат
має сталу довжину а .
30.
Л(2;0),а = 2.
31.
Л(-1;4), а = 3.
Задача 3. [ гл. 1, §2, приклади 3-9]
Розв'язати задані диференціальні рівняння, що допускають зниження
порядку.
У п.а) знайти загальний розв'язок.
У п.б) розв'язати задачу Коші.
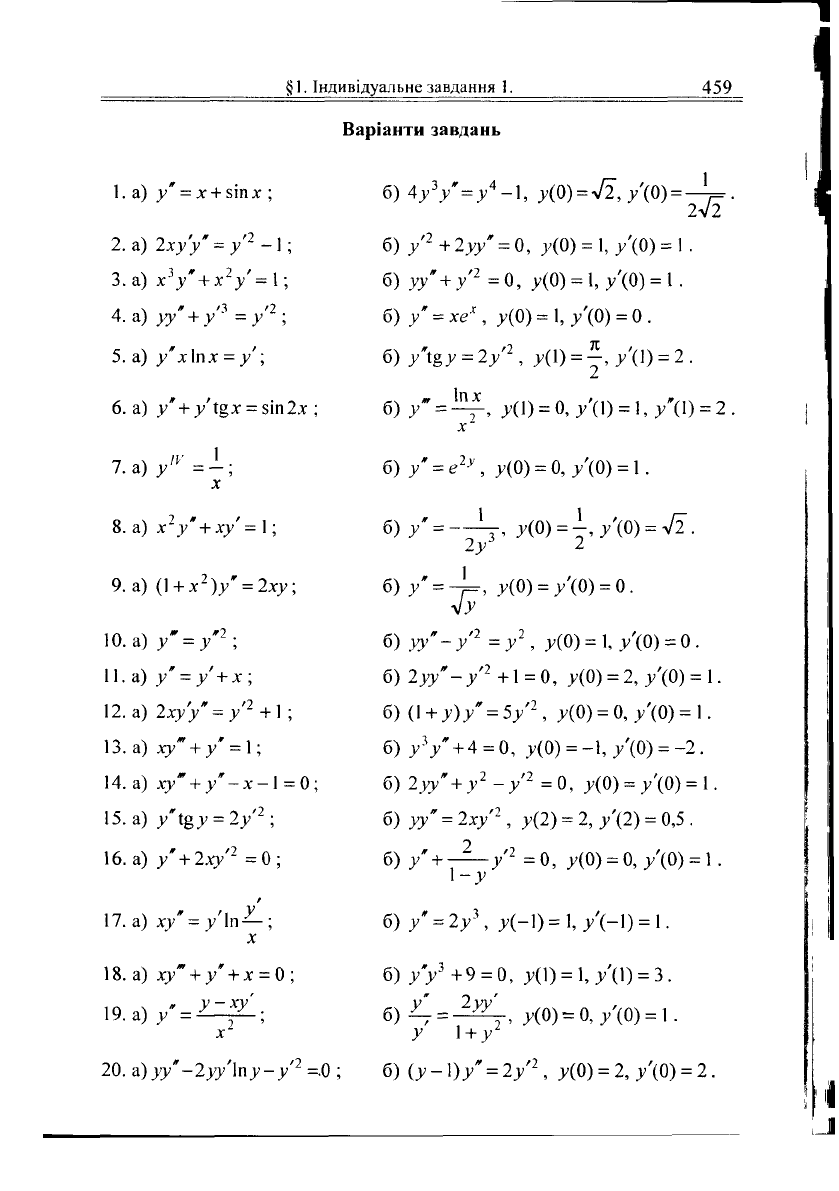
і;
1.
Індивідуальне завдання
1,
459
1.
а)
/
= х +
5Іпх;
б)
2.
а)
2ху'у"
= у'
1
-1;
б)
З.а)
3
• 2 ' і
17
+17 = 1;
б)
4.
а)
'
, '3 '2
>у
+у =у ;
б)
5.
а)
/хіпх
= у \
б)
6.
а)
у"'+
іЛ§х
=
зіп2х
;
б)
7.
а)
б)
х
8.
а)
2
* 'і
х
_у + ху = 1;
б)
9.
а)
(1+х
2
)/
= 2х.у;
б)
10.
а
11.
а
12.
а
13.
а
14.
а
15.
а
16.
а
17.
а
18.
а
19.
а
20.
а
Варіанти завдань
б)
4//=/-1,
Я0) =
л/2,/(0)=
'
2л/2
.»
, ..'2
X'
2у
3
'
2"
к
'
=
-7=' Я0) = /(0) = 0.
л/.У
/
= /
2
; б)
уу'-у'
2
=у
2
, Я0) = 1,/(0) = 0.
/
= /+*; б)
2уу"-у'
2
+\=0,
Д0) =
2,/(0)
= 1.
2х//
= у'
2
+1 ; б)
(1
+
у)
у"
= 5у'
2
, у(0) = 0, /(0) = 1.
х/
+ / = 1; б)// + 4 = 0, у(0) =
-1,/(0)
= -2.
х/
+
/-х-1=0;
б)
2уу"+у
2
-у'
2
=0, у(0) =
/(0)=1.
/1
8
у = 2/
2
; б) уу' =
2ху'
2
,
у(2) = 2, /(2) = 0,5 .
у"
+
2ху'
2
=0; б) / +
-?—/
2
=0, ДО) = 0, /(0) =
1
.
1-у
х/
= /1п^; б) / = 2/, Я-1) =
1,/(-1)=1.
х
х/
+ / + х = 0; б) //+9 = 0, у(1) = 1,/(1) = 3.
/
= ^;
б)4
=
^т,Я0)
=
0,/(0)
= 1.
х
у
1
+
Д
у/-2у/к7-/
2
=.0;
б) 7-1)/ = 2/
2
, у(0) = 2, /(0) = 2.

460
Глава 5, Типові розрахункові завдання
21.
а) /"сю 2х = 2/; б) у
3
у" = у
А
-16, у(0) = 2л/2, у'(0) = лІ2 .
22.
а)
ху"-у'-х5'т—
= 0; б) / = 505Їп
3
>'
сову,
у(]) = —, _у'(1) = 5.
х 2
23.
а)
у'-2у'сі§х=5Іп
3
х; б) у' = 32/ , у(4) = 1, /(4) = 4 .
24.
а) у~Щх = 2у"; б) / + 325Іпусо-г
3
у = 0, у(0) = 0, у'(0) = 4.
25. а) / + / = 5іпх; б) у\х
г
+1) = 2х/, _у(0) = 1, у'(0) = 3.
26.
а)
(\+е
х
)у'
+ у' = 0; б) (1 + у)/ = /
2
+у\ у(0) = 0, /(0) = 1.
27.
а) / + 4/ = соз2х; б)
уу"-у'
2
=
у
2
\пу,
у(0) = /(0) = 1.
28.
а)
х\пху"=
у"; б) / =
1
+ /
2
, у(0) = 1, /(0) = -1.
29.
а)(1+х
2
)/+2х/=х
3
; б)
уу"-2уу'\пу
= у'
2
, у(0) =
0,/(0)
=
1
.
ЗО.а) у"-Л— =
х
(
х
-\);
б) (2у + 3)/-2/
2
=0,Я0) =
0,/(0)
= 3.
х -1
31.
а)у
т
+у"і£х
= —1—; б) 4/
2
=
1
+ у'
2
, у(0) =
1,/(0)
= 0.
созх
Задача 4. [ гл /, $ 2, приклади 12-14]
Знайти загальний розв'язок однорідної о диференціального рівняння
зі сталими коефіцієнтами.
Варіанти завдань
І.а)/-2/+2у = 0; б) 4у"' + 3у" = 0 .
2.
а) / + б/+25у = 0; б) у" - у" - у'+ у = 0.
З.а) у' +
2у'+у
= 0; б) у" + 3/ + 2/ = 0 .
4.
а)/ + 4у' = 0; б) у"-\3у" + 12/ = 0 .
5.
а) 4у" + 4у'+ у = 0; б) у" - у" = 0 .
6. а) 9у"-6у' + у = 0; б)у" + у = 0.
7.
а) у'-4у' + 4у = 0; б) у'"-у" = 0.
8. а) у"-6у'+10у = 0; б) у'-Зу'+Зу'-у = 0.
9. а) у"-10у' + 25у = 0 ; б) у"-4у" + Зу' = 0.
10.
а) 4у" + 8у'-5у = 0 ; б) Зу" +/=0.
11.
а) /+9/ = 0; б) 9у~-6у"+у' = 0.
