Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Lagrangian Mechanics

∂∂

=⋅+⋅

∂∂

∑∑

kj ki ki



 αα.

Because



, while the matrix

⎡

⎤

∂∂

⎣

⎦

Xq is of rank s , it results that = 0

a ,

= 1,2,...,

, ⇔ == =, 1,2,..., , 1,2,...,

inkm0



α . Hence, if the conditions

= 0

a are fulfilled, then the constraints (18.2.9'') are scleronomic.

We can express the non-holonomic constraint relations with the aid of the virtual

generalized displacements too in one of the forms

δ= =0, 1,2,...,

aq k m,

(18.2.10)

∗

==0, 1,2,...,

aq k m .

(18.2.10')

By means of the possible generalized displacements, it results

Δ= =0, 1,2,...,

aq k m

(18.2.11)

∗

==0, 1,2,...,

aq k m



(18.2.11')

too. We can thus that, in case of catastatic constraints (holonomic or non-holonomic),

the set of virtual generalized displacements coincides with the set of possible

generalized displacements and the real generalized displacements belong to these sets.

We notice, from (18.2.10), that – in case of bilateral constraints – the virtual

generalized displacements are reversible; in case of non-strict unilateral constraints,

only some virtual generalized displacements are reversible (these which are equated to

zero in the constraint relations).

In case of a scalar function

( , ,..., ; )

qq qtϕ or of a vector function

( , ,..., ; )

qq qt, the operator of total differentiation with respect to time is of the

form

∂∂

tqt



(18.2.12)

This operator contains the operator of space differentiation

∂∂

qq and the operator

of time differentiation

∂∂t . Noting that

∂∂∂∂∂∂

=+ =+

∂∂∂∂∂∂∂∂∂∂

22 22

kkkk kk

q t qq qt tq qq tq



and assuming that the considered functions are of class

with respect to the

corresponding variables (in this case, according to Schwartz’s theorem, the mixed

derivatives are independent on the order of differentiation), we have the operator

relation

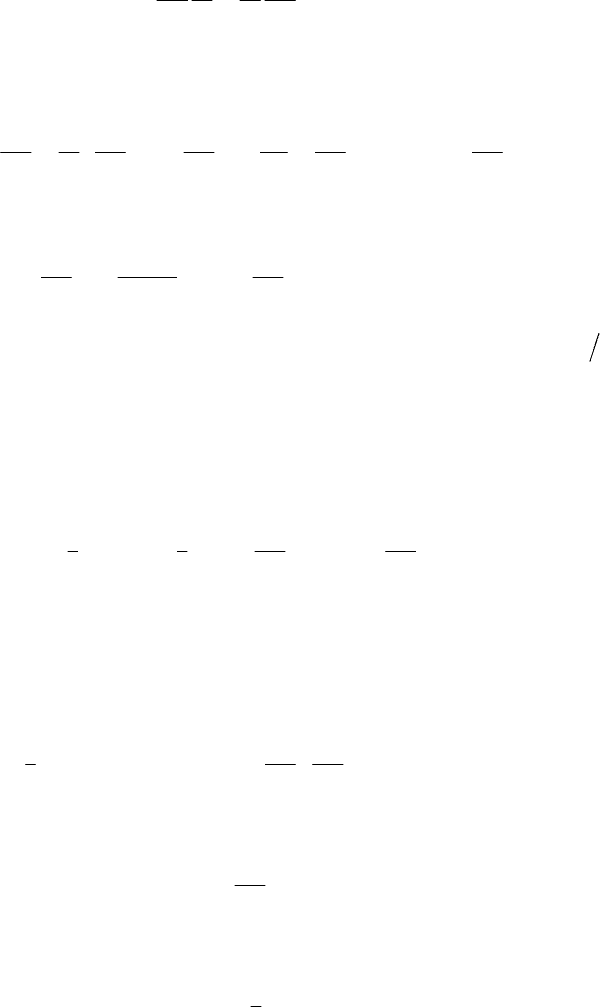
MECHANICAL SYSTEMS, CLASSICAL MODELS

∂∂

qt tq

(18.2.13)

Starting from (18.2.4') and taking into account (18.2.12), (18.2.13), we can calculate

the acceleration of the particle

P in the form

()

∂∂ ∂

∂

⎛⎞

== ++= +++

⎜⎟

∂∂ ∂ ∂

⎝⎠

vrrr r

avrr

dd d

iiii i

ijjiijji

jj j j

qq qq

ttq q tq q





 

wherefrom

∂∂ ∂

=+ + +=

∂∂∂ ∂

rr r

2 , 1,2,...,

ii i

ij j ji

jj j

qqqqin

qqq q





   

(18.2.14)

We have thus put in evidence the generalized accelerations

qqt ,

= 1,2,...,js.

18.2.1.3 Kinetic Energy. Work. Natural Systems

Starting from the expression (18.2.14') of the velocity of the particle

, we can

calculate the kinetic energy of the discrete mechanical system

S in the form

∂∂

⎛⎞⎛⎞

== +⋅+

⎜⎟⎜⎟

∂∂

⎝⎠⎝⎠

∑∑

vrr

ii i j i j i

Tm mq q



.

It results

=++

TT TT,

(18.2.15)

where

∂∂

===⋅=

∂∂

∑

, , , 1,2,...

jk k jk kj

Tgqqgg m jk s



(18.2.15')

is a quadratic form in the generalized velocities,

∂

== ⋅=

∂

∑

,,1,2,...

jj j i i

Tgqg m j s



(18.2.15'')

is a linear form in the generalized velocities, while

∑

000

Tgg m



(18.2.15''')

is a constant with respect to these velocities.

Lagrangian Mechanics

We notice that

≥

0T , being thus a non-negative quantity; the equality to zero takes

place in case of catastatic constraints (if the constraints are holonomic, then they are

scleronomic too). The linear form

T can have any sign; also this form vanishes in case

of catastatic constraints. Hence, in case of such constraints we have

∂

⎛⎞

== ≥

⎜⎟

∂

⎝⎠

∑

TT m q

 .

(18.2.16)

This quadratic form vanishes only if each bracket vanishes, hence for

∂

0, 1,2,...

qi n



We notice that the matrix ∂∂[]

Xq of the coefficients of this system of linear

equations is of rank

s ; it results ==0, 1,2,...,

qj s , the quadratic form

T being

positive definite. We remark, as well, that – in case of catastatic constraints – we have



too, the kinetic energy non-depending explicitly on time.

One can state that

≠=

⎡

⎤

⎣

⎦

0, det

gg g.

(18.2.17)

Indeed, otherwise, the system of linear equations

==0, 1,2,...,

jk k

gq j s , would

have non-trivial solutions; thus, a linear combination of these equations could lead to

jk k

Tgqq , without having all generalized velocities equal to zero. But the

quadratic form

T is positive definite, obtaining thus a contradiction. We mention also

that

T is a non-singular quadratic form (eventually, excepting the points (isolated) in

which the correspondence (18.2.1) (or (18.2.2)) is not one-to-one).

In general, the

+(1)2ss coefficients of the quadratic form

T are of the form

( , ,..., ; ),

jk jk

ggqqqt=

, 1,2,...,jk s= ; as well,

( , ,..., ; ),

ggqq qt=

1,2,...,js= . In case of catastatic constraints we have

( , ,..., ),

jk jk

ggqqq=

, 1,2,...,

ks= , ==

( , ,..., ), 1,2,...,

ggqq qj s.

The real elementary work of the given forces (external and internal) is given by

∂

=⋅=⋅

∂

∑∑

Fr F

dd d

ii i j

where we have taken into account (18.2.4); we can also write

∂

==⋅=

∂

∑

d d , , 1,2,...,

jj j i

WQqQ j s

(18.2.18)

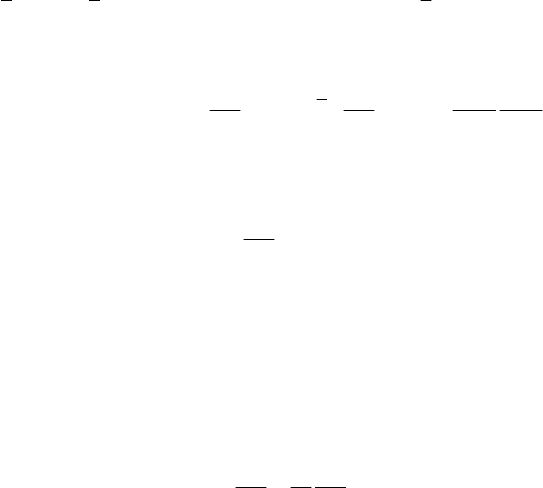
MECHANICAL SYSTEMS, CLASSICAL MODELS

By analogy,

Q are called generalized forces (by convention, we can assume that they

act upon the representative point

P ). The virtual work of these forces is expressed in

the form

δ=δ

WQq.

(18.2.19)

For the practical computation of the components (co-ordinates) of the generalized force,

we can fix all co-ordinates excepting one of them (let be

q , to which corresponds the

virtual displacement

q ); calculating δW in

E , one can obtain

Q , making then –

successively –

= 1,2,...,ks. We notice that a component

Q of the generalized force

has the dimension of a force only if the corresponding generalized co-ordinate

q has

the dimension of a length.

Supposing that the given forces

=F , 1,2,...,

in, derive from a simple quasi-potential

=rrrr

( ; ) ( , ,..., ; )

UtU t, then we can write =r

[(;);] (, ,..., ;)

UqttUqq qt,

obtaining thus a simple quasi-potential in generalized co-ordinates; indeed we can write

== ==

∂

∂∂

∂

=⋅=∇⋅=

∂∂ ∂

∂

∑∑ ∑∑

()

11 11

nn n

ii k

ji i

ii ik

qq q

wherefrom

∂

,1,2,...,

Qj s

(18.2.20)

the generalized forces being thus quasi-conservative. If

( , ,..., )

UUqq q is a

simple potential, then the corresponding generalized forces are conservative. But we

must notice that the existence of a quasi-potential for the given generalized forces does

not imply the existence of a quasi-potential for the given corresponding forces in the

space

∂∂

==− =

∂∂

[ ] , 1,2,...,

QU j s

qtq



(18.2.21)

then we say that the generalized forces are quasi-conservative, deriving from a

generalized quasi-potential

12 12

( , ,..., , , ,..., ; )

UUqq qqq qt  . We notice that the

generalized forces cannot depend on the generalized accelerations (because the given

forces cannot depend on the accelerations), so that the quasi-potential is of the form

UUq U ,

(18.2.22)

where

( , ,..., ; ), 0,1,2,...,

UUqq qtj s. Hence,

Lagrangian Mechanics

∂

⎛⎞

=− −+ =

⎜⎟

∂∂ ∂

⎝⎠

,1,2,...,

QqUjs

qq q



(18.2.21')

in case of quasi-conservative generalized forces; if the generalized forces are

conservative, corresponding to a generalized potential, where

( , ,..., )

UUqq q

= 0,1,2,...,

, then we have

= 0



By following gauge transformation →=+∂∂ =, 1,2,...,

kkk k

UUU qk sϕ ,

→=+

000

UUUϕ , where =

(,,...,;)

qq qtϕϕ is a function of class

C (to

have

∂∂ = ∂∂( )(d d ) (d d )( )

qt tq), hence by a transformation of the form

→=+ddUUU tϕ , we obtain the same generalized forces

Q . Hence, the genera-

lized quasi-potential from which derives a quasi-conservative generalized force is deter-

mined excepting the total derivative with respect to time of a function

ϕ of class

A field of quasi-conservative generalized forces is non-stationary, while a field of

conservative generalized forces is stationary.

The elementary work of conservative generalized forces is a total differential, being

of the form (18.1.22), in case of a simple potential, or of the form (18.1.22''), in case of

a generalized potential. If the generalized forces are quasi-conservative, deriving from a

simple quasi-potential, then the elementary work is of the form (18.1.23); if these

generalized forces derive from a generalized quasi-potential, then we get

()

∂

⎛⎞

=−− =− + = −

⎜⎟

∂

⎝⎠

00 0 0

dd d dd d d

jj jj j j

WUUtUq UUqUt Uq

  



(18.2.23)

We notice that the gauge transformation mentioned above for the generalized potential

does not affect this elementary work.

The mechanical systems which admit a simple or generalized potential (quasi-

potential) are called natural systems.

The generalized forces which do not derive from a simple quasi-potential can be

always expressed in the form

∂

=+ =

∂

, ( , ,..., ; )

QQUUqqqt

(18.2.24)

the elementary work being given by

()

=+ −dd d

WUQqUt



(18.2.24')

(,,..., )

UUqq q is a potential, hence if = 0U



, then the quantity =

QqP

represents the power of the non-potential generalized forces. By analogy with the

definitions given in

E and

E , the non-potential generalized forces

of zero

power (

= 0P ) are called gyroscopic generalized forces and depend, obviously, on the

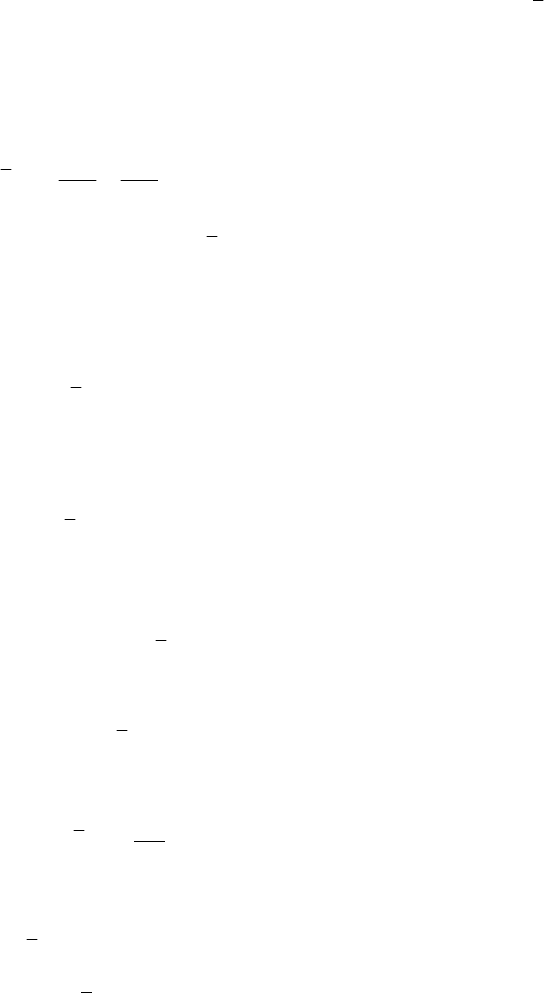
MECHANICAL SYSTEMS, CLASSICAL MODELS

distribution of the generalized velocities; in this case, the generalized forces

Q are

conservative. If the power of the non-potential generalized forces does not vanish, then

these forces are non-conservative. If

< 0P , then the corresponding generalized forces

are dissipative. The quasi-conservative forces (18.2.21') which derive from a

generalized quasi-potential are of the form (18.2.24), so that (we take

)

∂

⎛⎞

=− −=

⎜⎟

∂∂

⎝⎠

, 1,2,...,

QqUjs



(18.2.24'')

==0, 1,2,...,

Uj s



then it results = 0

Qq , the non-potential generalized forces

being thus gyroscopic. Hence, any generalized force which admits a generalized

potential is the sum of a generalized force which admits a simple potential and a

gyroscopic generalized force.

Let be, in general, a non-potential generalized force of the form

=− =,1,2,...,

jiji

Qqj sα  .

(18.2.25)

By a decomposition in symmetric and skew-symmetric parts of the tensor quantity

we observe that the non-potential generalized forces

=− =

()

,1,2,...,

Qqjsα  ,

(18.2.25')

where the quadratic form

()

Rqqα ,

(18.2.26)

called the Rayleigh dissipative function, is positive, are dissipative; indeed, we have

=− ≤

()

jj ij

Qq qqα.

We notice that

∂

=− =

∂

, 1,2,...,

Qjs

q

(18.2.26')

Analogously, the non-potential generalized forces

=− = =

[] []

, 1,2,...,

jii

ij ji

Qqqjsαα ,

(18.2.25'')

are gyroscopic, because

[]

jj ij

Qq qqα.

We observe that the notion of power of the non-potential generalized forces has a

signification larger than the classical one, coinciding with the latter one in case of a

potential (

= 0U



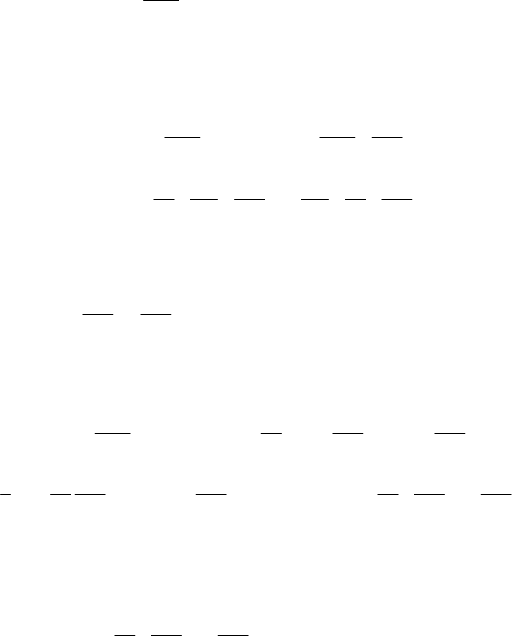
Lagrangian Mechanics

18.2.2 Lagrange’s Equations of Second Kind

The basic problem of motion of a discrete mechanical system S in the space

E is

reduced to the problem of motion of the corresponding representative point

P ,

subjected to the action of the generalized forces

=, 1,2,...,

Qj s, and to m

non-holonomic constraints (18.2.9) (or (18.2.9')) in the space

Λ (the representative

point

P is on a non-holonomic manifold with −sm dimensions, at the intersection of

m non-holonomic hypersurfaces). In what follows, we deduce Lagrange’s equations of

second kind in case of holonomic or non-holonomic constraints; a special attention will

be given to the case of quasi-conservative forces, by introducing Lagrange’s kinetic

potential.

18.2.2.1 Lagrange’s Equations in Case of Holonomic Constraints

Let be a discrete mechanical system S subjected to holonomic ideal constraints; the

motion of this mechanical system, hence the motion of the representative point

P in

the space

will be governed by the theorem of virtual work, written in the form

⋅δ =δ = ⋅δ

∑∑

rFr

ii ii

(18.2.27)

corresponding to the formulae (11.1.59), (11.1.63) and to the formula (18.1.52),

respectively. We calculate

∂

⋅δ = ⋅ δ

∂

∂∂

⎡⎛ ⎞ ⎛ ⎞⎤

=⋅−⋅δ

⎜⎟ ⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎝ ⎠⎦

∑∑

∑

rrr

rr r r

dd dd

iii

iii j

ii i i

mmq

ttq ttq

The formula (18.2.4') allows to write

∂∂

== =

∂∂

, 1,2,..., , 1,2,...,

injs



(18.2.28)

Using the operator relation (18.2.13) too, it results

() ()

∂∂

⎡⎛ ⎞ ⎤

⋅δ = ⋅ − ⋅ δ

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦

∂∂ ∂∂

⎡⎤⎡⎛⎞⎤

=−δ=−δ

⎜⎟

⎢⎥⎢⎥

∂∂ ∂∂

⎣⎦⎣⎝⎠⎦

∑∑

∑

rvv

1d d

2d d

iii

iiii i j

ii ii j j

jj jj

mm q

tq q

mmq q

tq q t q q





where we have introduced the kinetic energy

T . Taking into account also the formula

(18.2.19), we can write the equation (18.2.27) in the form

∂∂

⎡⎛ ⎞ ⎤

−−δ=

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦

tq q

(18.2.27')

MECHANICAL SYSTEMS, CLASSICAL MODELS

As a matter of fact, this represents the fourth form of the basic equation.

Because the constraints are holonomic, it results that the virtual generalized

displacements

q are independent; hence, we may write

∂∂

⎛⎞

−= =

⎜⎟

∂∂

⎝⎠

, 1,2,...,

Qj s

tq q

(18.2.29)

getting thus the equation of motion of the representative point

, that is Lagrange’s

equations of second kind (shortly, Lagrange’s equations), obtained be Lagrange in

1760. This system of differential equations of second order (the kinetic energy depends

on the generalized co-ordinates, the generalized velocities and time) allows to

determine the unknown functions,

( ), 1,2,..., , [ , ]

qqtj sttt== ∈.

The fundamental problem of mechanics remains, further, deterministic; starting from

the initial conditions (11.1.9), written for a discrete mechanical system, and taking into

account the relations (18.2.1) or (18.2.1') and (18.2.4'), we associate the initial

conditions of Cauchy type

() , ()

jj j

qt q qt q.

(18.2.30)

These conditions are univocally determinate (as we have seen in Sects. 18.2.1.1 and

18.2.1.2, in the general case). If

===

0, 0, 1,2,...,

qq j s , then we say that we

have to do with homogeneous initial conditions. Thus, the problem is entirely

formulated; the functions

()

qt must be of class

18.2.2.2 Case of Non-holonomic Constraints. Natural Systems. Kinetic Potential.

Conditions of Equilibrium

Let us suppose that the discrete mechanical system S , hence also the representative

point

P in the space

Λ , is subjected to <ms non-holonomic constraints, which are

expressed in the form (18.2.10), by means of the generalized displacements. In this case

the problem is reduced to the determination of the functions

==( ), 1,2,...,

qqtj s,

so that, besides Lagrange’s equations (18.2.29), the relations (18.2.27') be also satisfied,

for any virtual generalized displacements

q , which verify the constraint relations

(18.2.10); applying the method of Lagrange’s multipliers, used several times till now,

we can write

∂∂

⎡⎛ ⎞ ⎤

−−− δ=

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦

∑

kkj

Qaq

tq q



(18.2.31)

Assuming that the non-holonomic constraints are distinct, the matrix

[]

is of rank

m ; we can denote the generalized co-ordinates so that ≠=det[ ] 0, , 1,2,...,

ajk m,

which allows to determine univocally the multipliers

λ , by annulling the first m

Lagrangian Mechanics

square brackets. From the constraint relations we obtain the virtual generalized

displacements

δ=, 1,2,...,

ql m, as functions of the virtual generalized displacements

δδ δ

, ,...,

qq q , which can be considered to be independent; following the usual

reasoning, it follows that all square brackets vanish, so that we obtain Lagrange’s

equations in case of non-holonomic constraints (Lagrange’s equations with multipliers)

in the form

∂∂

⎛⎞

−=+ =

⎜⎟

∂∂

⎝⎠

, 1,2,...,

QRj s

tq q

(18.2.32)

where

∑

, 1,2,...,

kkj

Raj sλ ,

(18.2.33)

are the components of the constraint generalized force. To determine the

+sm un-

knowns (the functions

==( ), 1,2,...,

qqtj s, and the parameters

= 1,2,...,km) we have thus at our disposal s equations of Lagrange with multipliers

and

m constraint relations.

If the mechanical system

S has h holonomic constraints (18.2.3), which have not

been eliminated, then the constraint forces are

∂

∑∑

kkj l

λμ,

(18.2.33')

where

, 1,2,...,

lhμ = , are also Lagrange’s multipliers which must be determined,

taking into account supplementary constraint relations too.

In case of a natural system, the generalized forces derive from a simple or

generalized quasi-potential, being of the form (18.2.20) or of the form (18.2.21).

Introducing Lagrange’s kinetic potential (the Lagrangian, quantity of the nature of the

energy)

=+TUL ,

(18.2.34)

we can write the equations (18.2.32) in the form

∂∂

⎛⎞

−= =

⎜⎟

∂∂

⎝⎠

, 1,2,...,

Rj s

tq q



(18.2.35)

If we express the generalized forces in the form (18.2.24), the kinetic potential being,

further, given by (18.2.34), then the considered Lagrange equations become

∂∂

⎛⎞

−=+ =

⎜⎟

∂∂

⎝⎠

, 1,2,...,

QRj s

tq q

(18.2.36)

MECHANICAL SYSTEMS, CLASSICAL MODELS

putting in evidence the non-potential generalized forces.

If the constraints of the discrete mechanical system

S are holonomic, then these

equations become

∂∂

⎛⎞

−= =

⎜⎟

∂∂

⎝⎠

, 1,2,...,

Qj s

tq q

(18.2.37)

while in case of a natural system it results

∂∂

⎛⎞

−==

⎜⎟

∂∂

⎝⎠

0, 1,2,...,

tq q

(18.2.38)

Using the Euler–Lagrange operator, we can formally write

[

]

++= =0, 1,2,...,

TQR j s

(18.2.32')

as well as

[

]

+= =0, 1,2,...,

TQ j s,

(18.2.29')

[

]

+= =0, 1,2,...,

Rj sL ,

(18.2.35')

[

]

++= =0, 1,2,...,

QR j sL ,

(18.2.36')

[

]

+= =0, 1,2,...,

Qj sL ,

(18.2.37')

[

]

==0, 1,2,...,

jsL .

(18.2.38')

Thus, Lagrange’s equations take a simpler form, which is easier to handle in case of

natural systems; moreover, one obtains – in this case – interesting results concerning the

integration of the respective system of equations.

We notice that

=++

LLLL,

(18.2.34')

where we take into account (18.2.15), so that

==+− =+

0000

2211

,,TTUU TULL L ,

(18.2.34'')

in case of a generalized quasi-potential; if the quasi-potential is a simple one, then

. The mechanical systems which admit a kinetic potential are called mechanical

systems of first kind.

In general, we can consider a mechanical system the motion of which is specified by

a Lagrangian

11 12

( , ,..., , , ,..., ; )

qq qqq qt LL , even in the case in which the

system is non-natural, with the condition that the Hessian of this function with respect

to the generalized velocities be non-zero