Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Lagrangian Mechanics

()

=+ =

, 1,2,...,3

kk k k

MX Q R k n



(18.1.38'')

corresponding to the form given to this principle by Newton. The Cauchy–Lipschitz

theorem, stated in Sect. 11.1.1.5 (where we have used adequate notations for the

generalized force) ensures the existence and the uniqueness of the solution.

Introducing the generalized forces of inertia

=− =, 1,2,...,3

kkk

QMXk n



(18.1.39)

the law of motion becomes

++= =0, 1,2,..., 3

kkk

QQR k n,

(18.1.40)

and we can state.

Theorem 18.1.1 (d’Alembert). The motion of the representative point

subjected to

constraints in the space

takes place so that, at any moment, the point is in dynamic

equilibrium under the action of the given and constraint generalized force and of the

generalized force of inertia.

We introduce the lost generalized force of d’Alembert

=+=− =, 1,2,...,3

kkkk kk

QQQMXk n



(18.1.41)

In this case, the equations (18.1.40) become

+= =0, 1,2,..., 3

Rk n

(18.1.42)

and we can state

Theorem 18.1.1' (d’Alembert). The motion of the representative point P subjected to

constraints in the space

E takes place so that, at any moment, the constraint

generalized forces are equilibrated by the lost generalized forces of d’Alembert.

We notice that each of the Theorems 18.1.1 and 18.1.1' can be at the basis of the

Newtonian model, representing thus a differential principle of mechanics.

Formally, the equations (18.1.42), which represent the necessary and sufficient

conditions of dynamic equilibrium (characterizing, entirely, the motion of the

representative point

P subjected to constraints, hence of the dynamic discrete

mechanical system

S subjected to constraints), are not different from the relations

+= =0, 1,2,...,3

QR k n

(18.1.42')

which represent the necessary and sufficient conditions of static equilibrium of the very

same representative point

P (hence, of the same mechanical system S ). Hence, all

the considerations which can be made in case of problems of statics can be transposed

to similar problems with a dynamic character, replacing the given generalized force

MECHANICAL SYSTEMS, CLASSICAL MODELS

by the lost generalized force of d’Alembert

; as well, one observers that the results

concerning the problems of statics can be obtained by particularization, starting from

the general dynamic case.

If the momentum of the representative point

P is defined in the form

∑



(18.1.43)

then we can state a theorem of momentum

()

∑



(18.1.43')

As well, if the moment of momentum, with respect to the origin

O , of the

representative point

, is given by

−+ −+ −+

=∈

∑∑

3( 1) 3( 1) 3( 1)

1,, 1

Ojkl

ililil

ijkl

MXX



(18.1.44)

where we have introduced Ricci's symbol, then the theorem of moment of momentum is

written in the form

−+ −+ −+

⎡

⎤

=∈ +

⎣

⎦

∑∑

3( 1) 3( 1) 3( 1)

1,, 1

Ojkl

il il il

ijkl

XQ R



(18.1.44')

Starting from these two theorems, we obtain – easily – the corresponding

conservative theorems too, hence two first integrals of the considered system of

differential equations. Taking into account the above observations, the equations

()

−+ −+ −+

===

⎡⎤

+= ∈ + =

⎣⎦

∑∑∑

3( 1) 3( 1) 3( 1)

11,,1

0, 0

kk jkl

il il il

kijkl

QR X Q R

(18.1.45)

represent the necessary and sufficient conditions of rest of the representative point

with respect to a given frame of reference, in the case in which the discrete mechanical

systems

S is non-deformable.

The kinetic energy of the representative point

P is defined in the form

∑

TMX



(18.1.46)

and we can write

=+dd d

TWW,

(18.1.47)

where the elementary work is given by (18.1.15) and (18.1.15'); we state thus

Lagrangian Mechanics

Theorem 18.1.2 (theorem of kinetic energy). The motion of the representative point

subjected to constraints in the space

, takes place so that, at any moment, the

differential of the kinetic energy of thus point is equal to the elementary work of the

given and constraint generalized forces which act upon this point.

If we introduces also the powers of the given and constraint generalized forces in the

form

(18.1.46')

then the relation (18.2.47) becomes

TPP



(18.1.47')

We can state

Theorem 18.1.2' (theorem of kinetic energy; second form). The motion of the

representative point

P , subjected to constraints in the space

E , takes place so that,

at any moment, the derivative of the kinetic energy with respect to time of this point is

equal to the power of the given and constraint generalized forces.

In case of catastatic ideal constraints, the elementary work of the constraint

generalized forces vanishes (

=d0

W ; it will be shown in next section); hence

=dd.TW

(18.1.48)

If the given generalized forces derive from a simple or a generalized potential, then

=−ddWV, where =−VU in case of the simple potential and =−

VU in case of

the generalized potential. Introducing the mechanical energy

E , it results a mechanical

energy of the form

==+=,,constEhETVh .

(18.1.49)

We can state

Theorem 18.1.3 (conservation theorem of mechanical energy). The mechanical energy

of the representative point

P , subjected to catastatic ideal constraints in the space

E , is constant in time only and only if the given generalized forces derive from a

simple or generalized potential.

We notice that, in the manifold whit

3n dimensions, =Vh represents the level of

energy of the motion; because

> 0T , it results that the representative point P moves

in the domain

<Vh.

If we represent the arbitrary generalized forces in the form (18.1.25), then it results

()

⎛⎞

+= − = −

⎜⎟

⎝⎠

∑∑

ddd d

kk kk

TV Q X Ut QV U t



(18.1.50)

MECHANICAL SYSTEMS, CLASSICAL MODELS

where

=−VU corresponds to a simple quasi-potential; if =

( , ,..., )

UUXX X is

a simple potential, then we can write

()

∑

TV QV.

(18.1.50')

In the case of gyroscopic generalized forces we can write further a conservation

theorem of mechanical energy (of the form (18.1.49)), while if the forces are

dissipative, then the mechanical energy decreases.

18.1.2.2 Principle of Virtual Work. Lagrange’s Equations of the First Kind

We have seen that a discrete mechanical system S subjected to ideal constraints

verifies the relation (18.1.2); hence, a representative point

in the space

subjected to ideal constraints if the relation (considered by P. Appell as relation of

definition)

δ= δ=

∑

Rkk

WRX

(18.1.51)

is verified. Starting from d’Alembert’s principle (18.1.42), effecting a scalar product by

the virtual generalized displacements

X , summing for all indices and taking into

account the relation of definition (18.1.51) of the ideal constraints, we get the relation

()

δ= − δ=

∑∑

kk k kk k

XQMXX



(18.1.52)

which represents a necessary condition to describe the motion of the representative

point

. Assuming now that the condition (18.1.52) is fulfilled and that

holonomic

constraints of the form (18.1.11) and

m non-holonomic constraints of the form (18.1.7)

take place, we will use the method of Lagrange’s multipliers; we can thus write

== =

⎛⎞

∂

++δ=

⎜⎟

∂

⎝⎠

∑∑ ∑

11 1

kI jkk

kI j

λμ

where

, 1,2,...,

lpλ = , , 1,2,...,

jmμ = , are non-determinate scalars (Lagrange’s

multipliers) and where we took into account that one can invert the order of summation,

in a finite double sum. The

+pm constraints are linear and distinct, the matrix of the

coefficients

∂∂/

fX and

b being of rank +pm; we express thus the virtual

generalized displacements

δδ δ

, ,...,

XX X (we can always choose them so that

the determinant

+pm

of the respective coefficients in the constraints relations be

non-zero) by means of the other

−+3( )npm virtual generalized displacements,

where the latter ones can be considered as independent. We put the conditions that the

Lagrangian Mechanics

expressions in the brackets which multiply the first

+pm virtual generalized

displacements do vanish, determining thus, univocally,

+pmmultipliers

λ and

(these multipliers are given by a system of

+pm linear equations with +pm

unknowns, of determinant

≠ 0

The independent (and arbitrary) virtual generalized displacements

1pm

X ,

2pm

X , ..., δ

X can be all taken equal to zero, expecting only one, let be δ

X ; this

non-zero virtual generalized displacement being arbitrary, it results that the bracket by

which it is multiplied must vanish too. Making, successively,

=+ +1kpm ,

=+ +2kpm , ...,

, and taking into account the preceding considerations, it

results that all the brackets which multiply the virtual generalized displacements must

vanish. Finally, we can write

∂

++==

∂

∑∑

0, 1,2,...,3

kI jk

bk n

λμ

(18.1.53)

These equations are equivalent with the equations (18.1.42); in case of ideal

constraints, we can express the constraint generalized forces in the form

∂

=+=

∂

∑∑

, 1,2,...,3

kI jk

Rbkn

λμ ,

(18.1.54)

equivalent to (3.2.37). We can state (the relation (18.1.52) becomes a sufficient

condition too)

Theorem 18.1.4 (theorem of virtual work; d’Alembert-Lagrange). The motion of the

representative point

P , subjected to ideal constraints in the space

E , takes place so

that the virtual work of the lost generalized forces of d’Alembert, which act upon this

point, vanishes for all the systems of virtual generalized displacements of the respective

point.

Taking into account the equivalence between the relation (18.1.52), which represents

the form taken by Newton's equations, it results that the theorem of virtual work can be

considered as being a principle (the principle of virtual work or the principle of virtual

generalized displacements), because – starting from it – one can solve the fundamental

problems of dynamics in case of ideal constraints. The equation (18.1.52) is called also

the basic equation (the first form), while the equations (18.1.53) are known as

Lagrange’s equations of the first kind.

Introducing the virtual generalized velocities

∗

V , we can write the conditions

(18.1.52) in the form

∗

∑

(18.1.52')

too, the considered principle being thus called also the principle of virtual generalized

velocities.

MECHANICAL SYSTEMS, CLASSICAL MODELS

If some elements of the discrete mechanical system

S are rigid solids, then one

uses the formula (14.1.59) for the corresponding part of the virtual work.

In the static case, the principle of virtual work becomes

δ=

∑

QX ,

(18.1.52'')

being stated for the first time in 1717 by Jean I Bernoulli.

Let be a mechanical system

S of n particles

P , of weight g

m , = 1,2,...,in;

choosing a co-ordinate axis

Ox along the descendent vertical, we can write the virtual

work of these given forces in the form

()

⎛⎞

δ= δ=δ =δ = δ=

⎜⎟

⎝⎠

∑∑

gg gg

ii ii

Wmx mx M Mξξ

where

ξ is the applicate of the mass centre of the system S . We can thus state

Theorem 18.1.5 (E. Torricelli). A mechanical system subjected to ideal constraints and

to the action of its own weight is in equilibrium only and only for an extremum of the

applicate of its centre of mass.

Also this theorem can be considered to be a principle (Torricelli’s principle), which

may be applied for a certain sphere of problems (in case of a uniform gravitational

field). As we have seen in Sect. 4.1.1.7 (in case of a single particle), the position of

equilibrium is stable, labile or indifferent as the applicate of the mass centre has a

minimum, a maximum or is constant, respectively.

Using the expression (18.1.54) of the constraint generalized forces and the constraint

relations (18.1.6), (18.1.10), we can write the real elementary work (18.1.15') of the

constraint generalized forces, in case of ideal constraints, in the form

⎛⎞

=− +

⎜⎟

⎝⎠

∑∑

Rll

Wfbtλμ



(18.1.55)

In case of catastatic constraints (we have

= 0



= 1,2,...,lp

, and =

b ,

= 1,2,...,lm), the real elementary work of the constraint generalized forces vanishes;

indeed, in this case the real generalized displacements belong to the set of virtual

generalized displacements, the relation (18.1.51) implying

=d0

W . The conditions

in which take place the relations (18.1.48) and (18.1.49) are thus entirely justified.

Starting from the relations (18.1.6), we can write the constraint relations with the aid

of the possible generalized displacements

X , = 1,2,...,3kn, in the form

Δ+ = =

∑

0, 1,2,...,

jk k

bX b j m.

(18.1.56)

Introducing the possible generalized velocities

, 1,2,...,3

Vk n

Lagrangian Mechanics

we can write

+= =

∑

0, 1,2,...,

jk k

bV b j m,

(18.1.56')

too. Let be also other possible generalized velocities

+Δ

, for the same position

of the representative point

at the same moment t , so that

()

+Δ + = =

∑

0, 1,2,...,

jk k k

bV V b j m.

Subtracting the last two relations one from the other, it results

Δ= =

∑

0, 1,2,...,

jk k

bV j m

(18.1.56'')

Analogously, we can write

∂

Δ= =

∂

∑

0, 1,2,...,

Vl p

(18.1.56''')

Hence, these finite variations of the possible generalized velocities verify the relations

(18.1.7), (18.1.11) for virtual generalized velocities. One can thus write the basic

equation (18.1.52) in the second form

()

Δ= − Δ=

∑∑

kk k kk k

VQMXV



(18.1.57)

for a given position of the representative point

P , at a fixed moment t ; this form of the

equation plays an important rôle in case of the phenomenon of collision. If

V are

differential quantities, then these variations are virtual generalized velocities

(differences of possible generalized velocities) and we find again the form (18.1.52') of

the basic equation, as it has been shown by P. E. B. Jourdain, in 1908. The

corresponding principle is know also as Jourdain’s principle, being expressed in the

form

()

δ= − Δ=

∑∑

kk k kk k

XQMXX



(18.1.57')

By a total differentiation of the constraint relation (18.1.56') with respect to time, we

obtain the relations which must be verified by the possible generalized accelerations



= 1,2,...,3kn

, in the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

⎡⎤

++==

⎢⎥

⎣⎦

∑

0, 1,2,...

jk jk

jk k k

bA V j m

(18.1.58)

where

∂∂

∑

tXt

(18.1.59)

We consider also the possible generalized accelerations

+Δ

for the same

position and the same velocity of the representative point

P , at the same moment t ; as

above, we obtain the relations

Δ= =

∑

0, 1,2,...

jk k

bA j m.

(18.1.58')

Analogously, it results

∂

Δ= =

∂

∑

0, 1,2,...,

Al p

(18.1.58'')

We see that the finite variations of the possible generalized accelerations verify the

relations (18.1.7), (18.1.11), corresponding to the virtual generalized displacements. We

are thus led to the third form of the basic equation

()

Δ= − Δ=

∑∑

kk k kk k

AQMXA



(18.1.60)

for a given position and generalized velocity of the representative point

P , at a fixed

moment

t . If

are differential quantities, as Gauss and Gibbs have considered, we

can write this equation in the form

()

δ= − δ=

∑∑

kk k kk k

XQMXX

  

(18.1.60')

where these variations are virtual generalized accelerations (differences of possible

generalized accelerations) .

18.1.2.3 Gauss’s Principle. Hertz’s Principle

Let us suppose that a particle

P , of mass

m , of the mechanical system S

subjected to constraints is, at the moment

t , at the position

P of position vector r

velocity

and acceleration a

, = 1,2,...,in. If no force would act upon the particle

, then this one would effect the real displacement (Fig. 18.1)

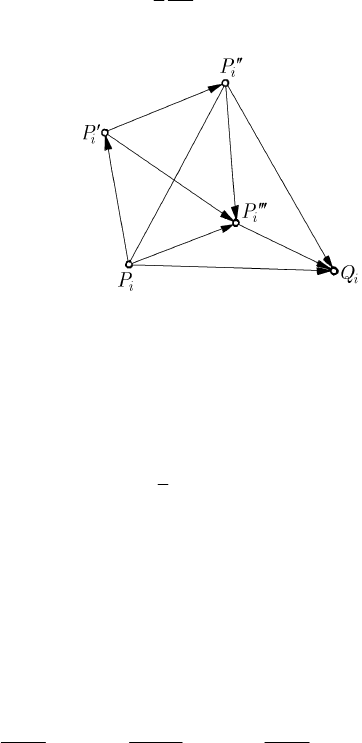
Lagrangian Mechanics

′

=Δ

ii i

PP t

JJJJG

(18.1.61)

during the time

t , while if upon this one would act upon only the given force F

, then

the particle would effect the real displacement

′′

JJJJG

, so that the derivation of the

particle

P in this motion would be given by the formula (5.1.21) in the form

()

′′

=Δ

PP t

JJJJG

(18.1.62)

Fig. 18.1 Gauss’s principle. Deviations

Finally, if the particle

P is acted upon both by the given and the constraint forces,

then it effects the real displacement

′′′

JJJJG

, in the time interval Δt ; the corresponding

deviation of the particle is

()

′′′

=Δ

ii i

PP t

JJJJG

(18.1.62')

collinear with the acceleration

. Let be also a possible displacement

JJJG

, different

from

′′′

JJJJG

, effected in the same interval of time Δt .

We notice that

′′ ′′′

JJJJJG

and

′′

JJJJG

represent the deviation of the particle

P from the

free motion, in the time interval

Δt to its real motion (the particle subjected to

constraints). Starting from the relation

′′ ′′ ′′′ ′′′

ii ii ii

PQ PP PQ

JJJJG JJJJJJG JJJJJG

, we can write

== = =

′′ ′′ ′′′ ′′′ ′′ ′′′ ′′′

=++⋅

∑∑ ∑ ∑

222

11 1 1

nn n n

ii i ii i ii i ii i i i

ii i i

mPQ mPP mPQ mPP P Q

JJJJJG JJJJJJG

We may also write

′′′ ′′′

=−

ii ii ii

PQ PQ PP

JJJJG JJJJJJG

JJJJG

, hence as a difference between a

possible and a real displacement (which is a possible displacement too); hence,

'''

JJJJG

MECHANICAL SYSTEMS, CLASSICAL MODELS

is a virtual displacement

δr

. On the other hand,

′′ ′′′ ′ ′′′ ′ ′′

=−

ii ii ii

PP PP PP

JJJJJG JJJJJJG JJJJJJG

; taking into

account (18.1.62), (18.1.62') and introducing the lost forces of d’Alembert of the form

(18.1.59), it results

()

== =

′′ ′′′ ′′′

⋅ =−Δ − ⋅δ =−Δ ⋅δ

∑∑ ∑

Far r

11 1

nn n

ii i i i i ii i i i

ii i

mPP PQ t m t

JJJJJG JJJJJG

Using the theorem of virtual work (in case of bilateral constraints) in the form

(11.1.63), we notice that this sum vanishes; if the constraints are unilateral, then the

relation (11.1.63'') takes place, the above sum being positive. As a conclusion, this sum

is non-negative in case of ideal constraints, so that

′′ ′′ ′′′

≥

∑∑

ii i ii i

mPQ mPP

JJJJG JJJJJJG

the equality taking place only if

′′′

≡

QP.

Gauss takes as measure of the deviation of the particle

P from its free motion, in

the real or in a possible motion, the constraint

()

′′ ′′′

or the constraint

()

′′′

respectively; in this case

≤= =

∑

ZZZ ZZ Z.

(18.1.63)

Hence, among all the possible motions of the discrete mechanical system

S , the

real motion is that for which the constraint

is minimal (any other possible constraint

Z is greater); but we notice that for all possible displacement must correspond the

same positions and the same velocities at the moment

, the accelerations being

different.

Taking into account the expression of the displacement

′′ ′′′

JJJJJG

, we can express the

constraint

Z in the form

()

==−

∑∑

11 11

iii

Φ ,

(18.1.64)