Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

Lagrangian Mechanics

while for the representative point

P we can write

()

==−

∑∑

11 11

kkk

ZQMX



(18.1.65)

From the condition of minimum of the constraint in the real motion it results

δ=0Z ; because only the accelerations vary, we get

()

===

δ= δ =− δ =− − δ =

∑∑∑

333

111

nnn

kk k k k kk k

kkk

ZXQMXX

ΦΦ Φ

  

(18.1.66)

equation which can be identified with the equation (18.1.60'). Starting from this

equation and from the relations (18.1.58'), (18.1.58''), written in the form

δ= =

∑

0, 1,2,...,

jk k

bX j m



(18.1.67)

∂

δ= =

∂

∑

0, 1,2,...,

Xl p



(18.1.67')

respectively, and introducing Lagrange’s multipliers – on the same way as in the

previous subsection – we find the equations (18.1.42). We can thus state

Theorem 18.1.6 (theorem of the least constraint; C. F. Gauss). The motion of the

representative point

, subjected to ideal constraints in the space

, takes place so

that the constraint

of this point has a minimum for virtual variations of the

generalized accelerations (the generalized co-ordinates and the generalized velocities

are considered constant).

We can also say that, in the same conditions concerning the position, the generalized

velocities and the generalized accelerations, the first variation of the constraint

the representative point must vanish (the constraint

is stationary along the trajectory

of the representative point

We have seen that the demonstration of this theorem implies the theorem of virtual

work, being thus equivalent to Newton’s principle. Also the theorem of the least

constraint, stated by Gauss in 1829, can be considered as a principle (the principle of

the least constraint), because – starting from it – one can find again Newton’s equations

in case of ideal constraints.

H. Hertz considers that the given generalized forces, which act upon the mechanical

system

S , can be replaced by given constraints between this system and neighbouring

systems which act upon it; thus, he studies only mechanical systems which are not acted

upon by given generalized forces (

= 0

). As well, to obtain a geometric

interpretation, he assumes that the generalized masses

are equal to unity (hence,

===

12 3

...

MM M

). Thus, it results

⎛⎞

⎜⎟

⎝⎠

∑∑



(18.1.68) .

MECHANICAL SYSTEMS, CLASSICAL MODELS

In case of a single particle, of co-ordinates

123

,,xxx, we have (we can assume, in

this case, that the mass

m is not equal to unity)

()

=++=a

222 2

123

Zxxx  

(18.1.69)

where

a is the acceleration in the considered motion; we obtain thus δ=δZaa. Using

Frenet’s frame of reference, we can write



;

this sum of squares is minimal if

= 0v



(which takes place because the given force is

equal to zero and one assumes that the constraints are catastatic, so that

=d0

W ,

while the constraint force has no component along the tangent to the trajectory), hence

if the motion is uniform and if the curvature

1/ρ is minimal. Hence, the trajectory of

the point must be of minimal curvature (as near as possible to a straight line).

In case of a discrete mechanical system

S , of representative point P , we can

express the kinetic energy in the form (with the above considerations)

()

⎛⎞

== ==

⎜⎟

⎝⎠

∑∑

11 1d1

22d2d2

TX s



where

=+++

222 2

12 3

d d d ... d

sXX X is the square of the arc element in the space

E . Because there are not generalized forces and assuming that to constraints are

catastatic (

=d0

W ), it results that = const.T As we can notice,

⎛⎞

===

⎜⎟

⎝⎠

∑∑

dd dd

,1, 0

dd d

kk kk

XX XX

ss s



so that

Xss





;

in the mentioned conditions, we have

==0sv





, hence the motion of the

representative point on its trajectory is uniform. We can thus replace the quantity

Z by

the quantity

()

== =

∑∑ ∑

11 1

nn n

ki i

(18.1.70)

where we define by

K the curvature of the path travelled through by the system (in a

certain sense, a measure of the curvatures of the paths of all the particles

which form

Lagrangian Mechanics

the system

S ); the minimum of the curvature K corresponds, obviously, to the

minimum of the constraint

Z . We can thus state

Theorem 18.1.7 (theorem of the least curvature; theorem of the most straight path;

H. Hetz). The motion of the discrete mechanical system

S , subjected to ideal

catastatic constraints, in the absence of the given generalized forces (in spontaneous

motion) and assuming a mass of equal generalized components, takes place, starting

from a given initial uniform motion, so that the curvature

K of the path travelled

through by the system be minimal, with respect to any other possible path (the path

travelled trough be the most straight possible one).

As in the preceding cases, we can consider this theorem as a principle (the principle

of least curvature or the principle of the most straight path). We mention that, because

of the conditions which are imposed, this principle is not so easy to apply; but the

connections to Lagrangian mechanics and to relativistic mechanics are interesting.

Starting from a constraint relation of the form

12 12

( , ,..., , , ,..., ; ) 0, 1,2,...,

XX X XX Xt j mϕ

 

which is not necessarily linear in the generalized velocities, and effecting a total

derivative with respect to time, we obtain

∂∂

⎛⎞

++==

⎜⎟

∂

⎝⎠

∑

0, 1,2,...,

XX j m

ϕϕ





Varying only the accelerations, we find the relations

∂

δ= =

∂

∑

0, 1,2,...,

Xj m





(18.1.71)

which are of the same form as the relations (18.1.67) (

=∂ ∂

bXϕ



We can thus state that Gauss’s principle can be applied even if the kinetic constraint

relations are not linear in the generalized velocities, having thus a larger sphere of

applicability than the principle of virtual work (for which the mentioned relations must

be linear in the generalized velocities).

We remark that Jourdain’s principle has a position somewhat intermediary between

the d’Alembert-Lagrange principle and Gauss's principle.

18.1.2.4 Applications

Let be a particle P subjected to move on a deformable surface of equation

123

(,, ;) 0fx x x t (we use the notations in the space

E ); the constraint relation can

be written in the form

δ=

fx . If we use the principle of virtual work in the form

δ=0

(18.1.72)

and if we eliminate, e.g., the virtual displacement

, then we get

MECHANICAL SYSTEMS, CLASSICAL MODELS

⎛⎞⎛⎞

−δ+−δ=

⎜⎟⎜⎟

⎝⎠⎝⎠

,1 ,2

131232

,3 ,3

ΦΦ ΦΦ

To satisfy this relation for any virtual displacement δ

x and δ

x , the two brackets

must vanish, hence

,1 ,2 ,3

123

fff

ΦΦΦ

(18.1.73)

This result corresponds to that obtained in Sect. 6.2.2.2 by the method of Lagrange’s

multipliers.

Fig. 18.2 Motion of a particle on a fixed or movable or deformable sphere

In particular, let be a particle

P in motion on a sphere S , fixed or movable and

deformable

′′

−=rr

()

l , of centre

′′

=rr()

t and radius = ()llt (Fig. 18.2).

Noting that

′′ ′′

−−=−rr rr

grad[( ) ] 2( )

l , Lagrange’s equation of the first kind

is of the form

()

′′′

=−rrr



, λ indeterminate scalar (we assume that the given

force is equal to zero); shifting the origin to the centre of the sphere, we can write the

equation of motion in the form

′

=−rrr

 

′′

=−rr r

, too, with the constraint

rl, putting thus in evidence the complementary force of transportation

′

−r



of the

movable frame of reference (in general, non-inertial). By a vector product by

r and by

a scalar product by



, respectively, we get

()

′′

×=× = − ⋅

rr r r r r r r

ddd

ttt

  

′



(hence, if the movable frame is inertial, the centre of the sphere having a

rectilinear and uniform motion), then we have

×=rr C



, =C const

JJJJG

, wherefrom

0⋅=Cr and

dd 2tllλ



; hence, the trajectory is a great circle of the deformable

sphere (the intersection of the plane

0⋅=Cr with the sphere). In particular, if the

radius

l of the sphere is constant, then the trajectory is a geodesic of it.

Let now be a particle

P which moves on a deformable curve of equations

123

(,, ;) 0

fxxxt , = 1,2k (in the space

E ); the constraint relations can be written

Lagrangian Mechanics

in the form

δ=

fx ,

= 1, 2k

. Associating the condition (18.1.72) and eliminating

the virtual displacements, we obtain

133

1,1 1,2 1,3

2,1 2,2 2,3

0fff

fff

ΦΦΦ

(18.1.74)

relation which – together with the constraint relations – allows to determine the motion

of the particle (see Sect. 6.2.2.1 too, where Lagrange’s multipliers are used).

Fig. 18.3 Motion of a particle on a movable circle of variable radius

Let us study, in particular, the motion of a particle

P on a circle C , movable and of

variable radius, represented by the intersection of the above considered sphere

S with

the plane

′′

⋅− =

rr()0

α , = ()tαα, which passes through

′

and is normal to α

(Fig. 18.3). As in the preceding case, in the absence of the given force, we can write the

equation of motion in the form

′

=+ −

rr r

λλ

 

α ,

,λλ indeterminate scalars,

′′

=−

rr r

, with the constraint relations =

rl, =0⋅ rα . By a vector product by

r and successive scalar products by r



and α , respectively, we get

()

′

×= ×+

rr r r



α ,

′

=−⋅+⋅

rrrrr

λλ



α ,

⋅= −⋅

 

ααα.

= const

JJJJG

α (hence, if the circle C is in a plane of fixed direction), then we have

⋅=r 0



α , ⋅=r 0



α too (according to the constraint relations). Thus, it results

′

=⋅



α ,

hence the component

λ α normal to the plane ⋅=r 0α , of the constraint force (the

component contained in the plane is

λ ). If

′



(the movable frame of reference

MECHANICAL SYSTEMS, CLASSICAL MODELS

is inertial), then the constraint force is contained in the plane of the circle, which has a

fixed orientation.

Let be two particles

P and

P of masses

m and

m and position vectors r

and

, upon which act the given forces F

and F

, respectively; we assume a constraint

relation at distance of the form

−=rr

()l , = ()llt, which can be written as

−⋅δ−−⋅δ=rr r rr r

12 1 12 2

() () 0. The principle of virtual work is written in the

form

⋅δ + ⋅δ =rr

11 22

0ΦΦ , being thus led to Lagrange’s equations of the first kind

() ()

+−= −−=rr rr

112 212

,λλ00ΦΦ.

(18.1.75)

We obtain thus

0ΦΦ . Assuming that =+FgF

1112

m , =+FgF

2221

m ,

=gg()t , where F

and F

are internal forces ( +=FF

12 21

0 ), it results

+=+rr g

11 22 1 2

()mm mm

 

, wherefrom

()

+=+ ++

∫∫

rr CC

11 22 1 2 1 2

d()d

mm mm g t

τττ

with

=CC

,const

JJJJG

; hence, the centre of mass C has a motion of acceleration g()t ,

being situated on the segment of a line

PP , so that

===

12 12

ml ml

CP CP l P P

mm mm

The particles

P and

P will be at any moment on two concentric spheres of radii

CP and

CP , respectively (hence, remains to be studied the problem of motion of a

particle on a given sphere). In the particular case of two heavy particles, the mass centre

C will describe a parabola situated in a vertical plane and having a vertical axis; the

particles will be in a plane of fixed orientation, their motion with respect to the centre

C taking place after the law of areas.

The analytic methods of computation have been developed, especially, in case of

discrete mechanical systems; however, they can be applied successfully also to

problems concerning continuous mechanical systems. We consider thus a perfectly

flexible, inextensible and non-torsionable thread, of given length

l , fixed at the points

P and

P , acted upon by forces p()s on unit length. The principle of virtual work is

written in the form

()

⋅δ = = −

∫

rpa

d0,

s μΦΦ,

(18.1.76)

where

()sμ is the linear density, while a()s is the acceleration of an arbitrary point

P . The relation = r

d(d)s leads to δ=⋅δrr

d(d)d (d)ss ; because the thread is

inextensible, we have

δ=(d ) 0s , so that the constraint relation (which takes place for

all the elements of arc) is written in the form

Lagrangian Mechanics

()

⋅δ =

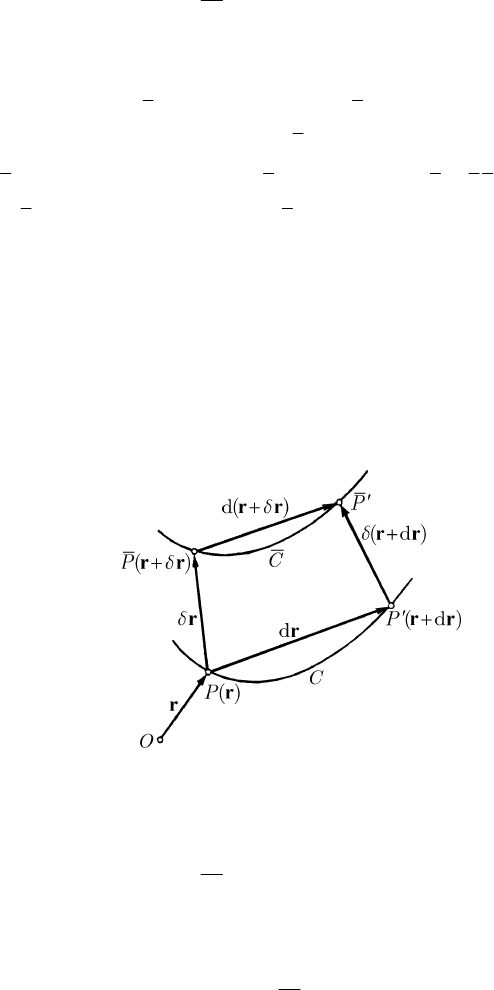
Starting from the points

of the curve

and considering a given system of virtual

displacements (at any point

P corresponds a virtual displacement δr at the moment

t ), we obtain the points

, which form the curve

. If r()P and

′

rr(d)P are two

neighbouring points on the curve

C and +δrr()P is a corresponding point on the

curve

C , one can reach the point

′

on the path

′

+PP PP

JJG JJJJG

or on the path

′′′

+PP P P

JJJG

(Fig. 18.4); hence, the point

′

can be specified by

+δ+ +δ=+ +δ+rr rrrr rrd( ) d ( d ) ,

wherefrom

δ=δrrd( ) (d ) , so that the two operators are linked by the relation

δ=δdd.

(18.1.77)

Obviously, the considerations made above involve, at the most, holonomic

constraints; the relation of permutation (18.1.77) takes place just in such a case.

Fig. 18.4 Displacements of a particle laying on a curve

The constraint relation becomes

()

⋅δ=

so that Lagrange’s equation of the first kind will be

()

⎡⎤

⋅δ + ⋅ δ =

⎢⎥

⎣⎦

∫

dd0

λΦ .

Integrating by parts

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

⋅δ= ⋅δ − δ⋅

∫∫

rr r

01 01

dd d

PP PP

ss s

λλ

and noting that

δr vanishes at the fixed points

P and

P , it results

()

⎡⎤

+⋅δ=

⎢⎥

⎣⎦

∫

dd 0

Φ .

Because this relation must take place for any virtual displacement

δr , we obtain

−=

λ 0Φ ;

introducing the tension in the thread

==−

λ ,

we can write

0Φ ,

(18.1.78)

finding thus again the equation (12.2.10) of motion of the thread.

We present now some simple applications too, eventually with a practical character.

Fig. 18.5 Motion of a coach on a railway in a curved line

Let use consider a railway which, on a certain length, follows a curve of curvature

radius

ρ . D’Alembert’s principle, written for the mass centre C of a coach, in the

normal plane to the curve (Fig. 18.5), leads to

++ =GNF 0

, where G is the

weight of the coach,

N is the normal reaction of the ground, while

is the

transportation force of a non-inertial frame of reference (the centrifugal force), of

magnitude

Lagrangian Mechanics

To can verify the equation of dynamic equilibrium, one must give to the ground an

inclination of angle

α , so that −=sin 0

NFα , −=cos 0NGα , whence

tan

;

the exterior rail must be superelevate to a height

=≅sin tanhl lαα

(

is the

clearance of the railway), so that

≅

gρ

(18.1.79)

at an arbitrary point of the curve.

Fig. 18.6 Belidor’s crane bridge

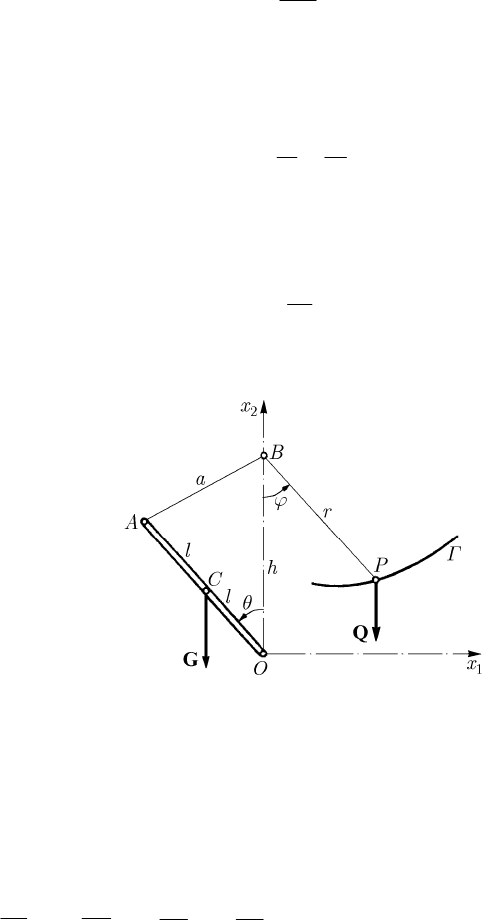
Let be now a rigid bar

OA of weight G , which is rotating in a vertical plane, about

a fixed point

. A perfectly flexible, inextensible and non-torsionable thread, which

passes over a fixed pulley

B , situated on the vertical line of O , connects the point A

to a point

P , where is suspended a weight Q . One must find the locus of the point P

(a curve

), so that the bar AO be in indifferent equilibrium (Fig. 18.6). The bar AO

models Belidor’s crane bridge. We denote

====> = =2, , , , 0, ,OA l AB a BP r OB h h BOA OBPθϕ;

we choose

-axis, the

-axis being horizontal, so that =

cos

xlθ ,

=−

cos

xhrϕ . The constraint relations are +=ar L, = ()rrϕ , where L is the

length of the thread. The mechanical system has only one degree of freedom and its

MECHANICAL SYSTEMS, CLASSICAL MODELS

position can be specified by the angle

ϕ . The principle of virtual work is written in the

form

−δ − δ =

Gx Qx . We have

δ+δ=0ar ,

′

δ= δ()rrϕϕ

, =+−

222

44cosalhlhθ ,

hence

δ= δ2sinaa lh θθ; in this case

′

δ=− δ=−δ=δ= δ

sin ( )

222

aaa

xl a rr

hhh

θθ ϕ ϕ.

On the other hand,

[

]

′

δ=− δ+ δ= − δ

cos sin ( )sin ( )cos

xrrrrϕϕϕϕϕϕϕϕ

We obtain thus the condition of equilibrium

[]

′′

−+ − =() ()cos ()sin 0

rQr r

ϕϕϕϕϕ,

which determines the corresponding angles

ϕ . We get thus the differential equation

{

}

−

′

−+=

[()]

cos ( ) ( )sin 0

GL r

QrQr

ϕϕ ϕϕ

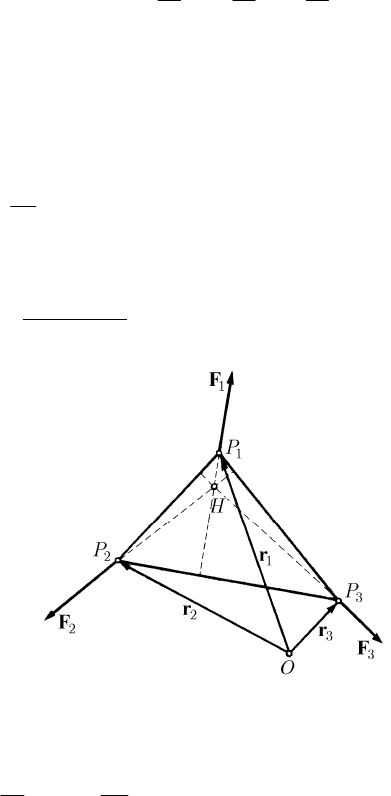
Fig. 18.7 Equilibrium of three particles acted upon by three forces in a particular case

By integration, we obtain

−+ =

() () ()cos const.

GPL

rrQr

ϕϕϕϕ

Hence, the equation of the curve

r is of the form