Тен В.А., Абайылданова К.Ж. Подземная гидромеханика
Подождите немного. Документ загружается.

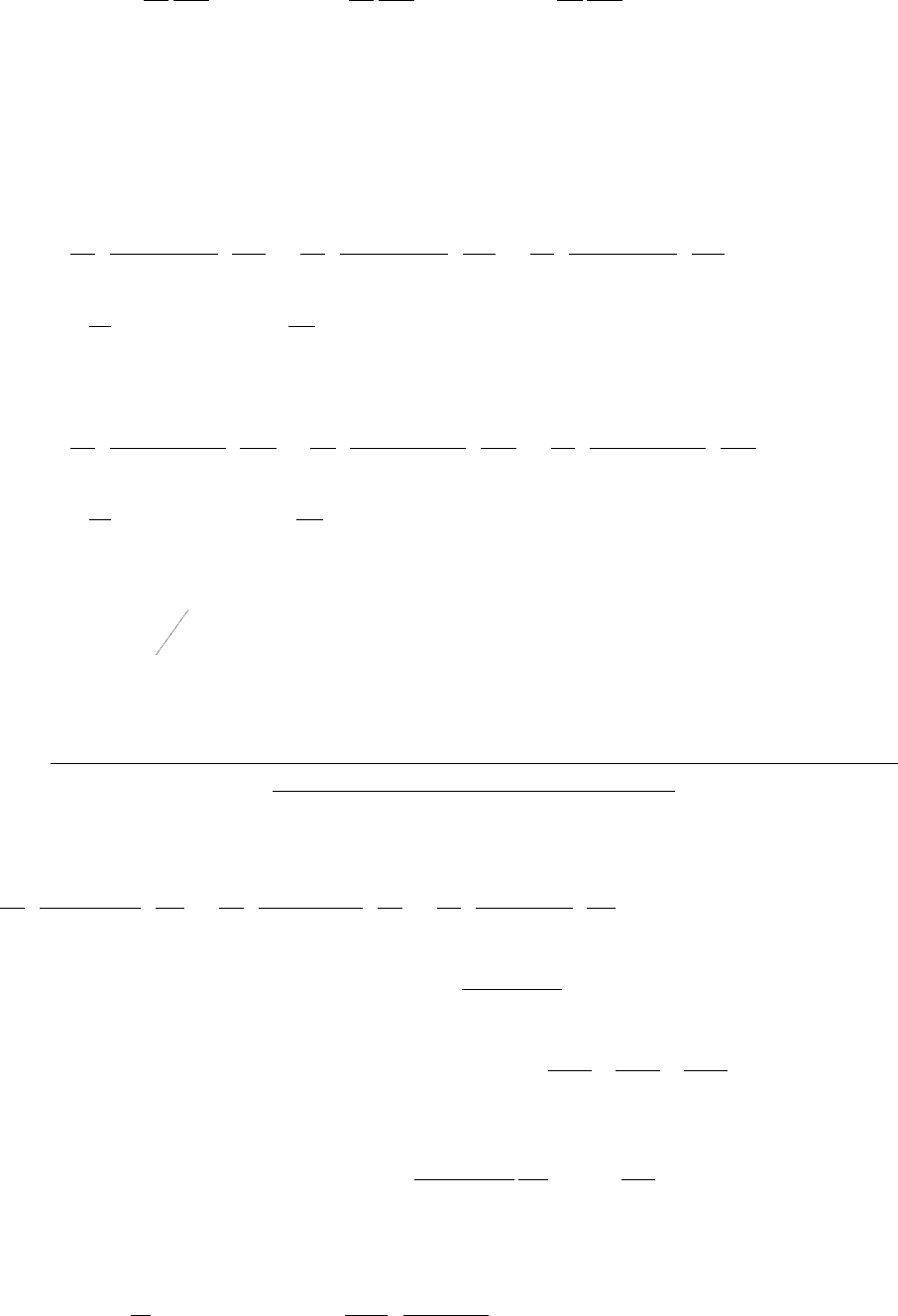
,
22
2
x
Pk
x
∂
∂
−=
µ
ϑ
,
22
2
y
Pk
y
∂
∂
−=
µ
ϑ
,
22
2
z
Pk
z
∂
∂
−=
µ
ϑ
(10)
К
уравнениям
(7)-(10)
должны
быть
добавлены
зависимости
плотности
ρ
,
пористости
1
m и
2
m
,
проницаемостей
1
k и
2
k
от
давлений
1
P
и
2
P
.
Подставив
(9)-(10)
и
(5)
для
упругой
жидкости
или
(6)
для
газа
в
(7)
и
(8),
получим
систему
уравнений
неустановившейся
фильтрации
жидкости
или
газа
в
трещиновато
-
пористой
среде
(
ТПС
)
в
виде
:
(
)
(
)
(
)
(
)
(
)
(
)
( ) ( )
[ ]
( ) ( )
[ ]
,
12111
111111111111
PfPfPmP
t
z
PPkP
zy
PPkP
yx
PPkP
x
−−
∂
∂
=
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
µ
ρ
αρ
µ
ρ
µ
ρ
µ
ρ
o
o
(11)
(
)
(
)
(
)
(
)
(
)
(
)
( ) ( )
[ ]
( ) ( )
[ ]
,
12222
222222222222
PfPfPmP
t
z
PPkP
zy
PPkP
yx
PPkP
x
−−
∂
∂
=
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
µ
ρ
αρ
µ
ρ
µ
ρ
µ
ρ
o
o
(12)
где
f(P)=P -
для
упругой
жидкости
;
( )
o
P
P
Pf
2
)(
2
=
-
для
идеального
газа
.
Уравнения
(11)
и
(12)
решаются
при
соответствующих
начальном
и
граничном
условиях
.
Установившаяся одномерная фильтрация жидкости и газа в трещиноватом (Т) и
трещиновато-пористом пласте (ТПП)
Рассмотрим
чисто
трещиноватый
пласт
(
ТП
),
в
которых
проницаемость
изменяется
по
(2)-(4).
В
этом
случае
уравнение
(11)
принимает
вид
:
(
)
=
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
z
PPkP
zy
PkP
yx
P
PkP
x
µ
ρ
µ
ρ
µ
ρ
)()(
)()()(
11
0
(13)
Введем
функцию
Лейбензона
(
)
(
)
cdP
PkP
+∫=Φ
µ
ρ
1
(14)
С
учетом
(14)
уравнение
(13)
принимает
вид
:
=
∂
Φ∂
+
∂
Φ∂
+
∂
Φ∂
2
2
2
2
2
2
zyx
0
(15)
По
аналогии
с
установившейся
фильтрацией
жидкости
в
недеформируемой
среде
массовый
дебит
равен
:
(
)
(
)
F
dS
d
F
dS
dP
PkP
QQ
ж
⋅
Φ
−=⋅−=⋅=
µ
ρ
ρ
1
(16)
Рассмотрим
фильтрацию
несжимаемой
жидкости
(
)
const=
ρ
.
Тогда
с
учетом
(3)
( )
(
)
c
e
k
dek
PP
cP
PP
+⋅=⋅∫=Φ
−−
+
−−
αµ
ρ
µ
ρ
α
α
o
o
o
o
1
1
(17)
Значение
функции
Л
.
С
.
Лейбензона
на
границах
:
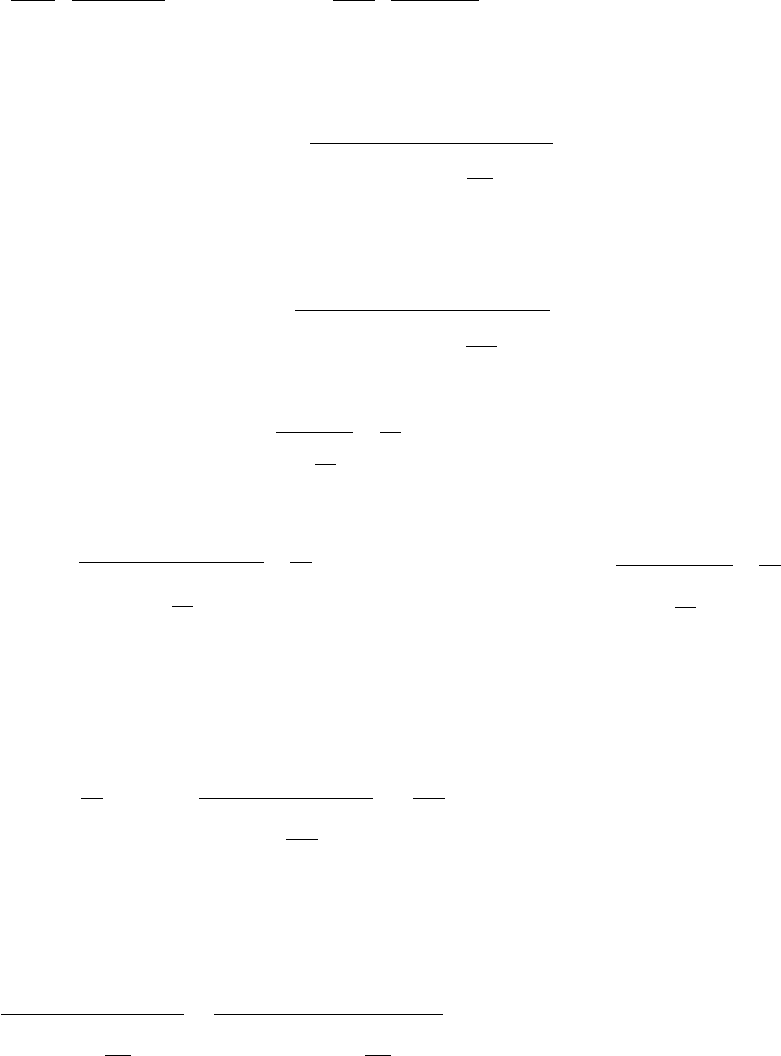
(
)
,
1
с
e
k
к
PP
к
+⋅=Φ
−−
αµ
ρ
α
o
o
(
)
c
e
k
c
PP
с
+⋅=Φ
−−
αµ
ρ
α
o
o
1
(18)
Если
принять
к
PP =
o
,
то
(
)
[
]
,
ln
12
1
c
к
РР
ж
r
r
ekh
Q
ск
⋅⋅
−
=
−−
αµ
ρπ
α
o
(19)
а
объемный
дебит
(
)
[
]
c
к
РР
r
r
ek
Q
с
ln
12
1
⋅⋅
−
=
−−
αµ
π
α
o
o
(20)
Подставляя
в
формулу
c
к
c
к
ск
к
r
r
r
r
РР
РР
ln
ln
−
−=
значения
,,,
ск
ΦΦΦ
получим
( ) ( )
(
)
(
)
r
r
r
r
ee
ee
к
c
к
PPPP
PPPP
cк
r
ln
ln
−−−−
−−−−
−
−=
oo
oo
αα
αα
,
если
к
PP =
o
,
( )
(
)
r
r
r
r
e
e
к
c
к
РР
РР
ск
к
ln
ln
1
1
−−
−−
−
−=
α
α
откуда
распределение
давления
( )
−
−+=
−−
r
r
r
r
e
PP
к
c
к
РР
к
ск
ln
ln
1
1ln
2
1
α
, (21)
В
ТПП
дебит
скважины
складывается
из
дебита
жидкости
притекающей
из
трещин
и
поступающей
из
пористых
блоков
:
(
)
(
)
[
]
c
к
РР
c
к
ск
r
r
ehk
r
r
РРhk
Q
ск
ln
12
ln
2
1
2
⋅⋅
−
+
−
=
−−
αµ
π
µ
π
α
o
(22)
Для
установившейся
фильтрации
идеального
газа
в
чисто
ТП
зависимость
проницаемости
от
давления
можно
принять
линейной
по
формуле
(4).
В
этом
случае
функция
Лейбензона
принимает
вид
:

(
)
(
)
(
)
[
]
( )
[ ]
( )
,
32
1
1
1
32
1
2
1
11
с
РР
Р
k
Р
cdPPPdPP
k
Р
cdP
РРk
Р
Р
cdP
PkP
к
ат
ат
к
ат
ат
к
ат
ат
+
+−=
=+∫+∫−=
=+
−−
⋅∫=+∫=Φ
αα
µ
ρ
αα
µ
ρ
µ
α
ρ
µ
ρ
o
o
o
(23)
Объемный
дебит
,
приведенный
к
атмосферному
давлению
−
⋅⋅+−=
ск
с
к
c
к
ат
ат
РР
Р
Р
r
r
Р
hk
Q
2
1
3
2
3
1
ln
α
α
µ
π
o
(24)
