Тен В.А., Абайылданова К.Ж. Подземная гидромеханика
Подождите немного. Документ загружается.

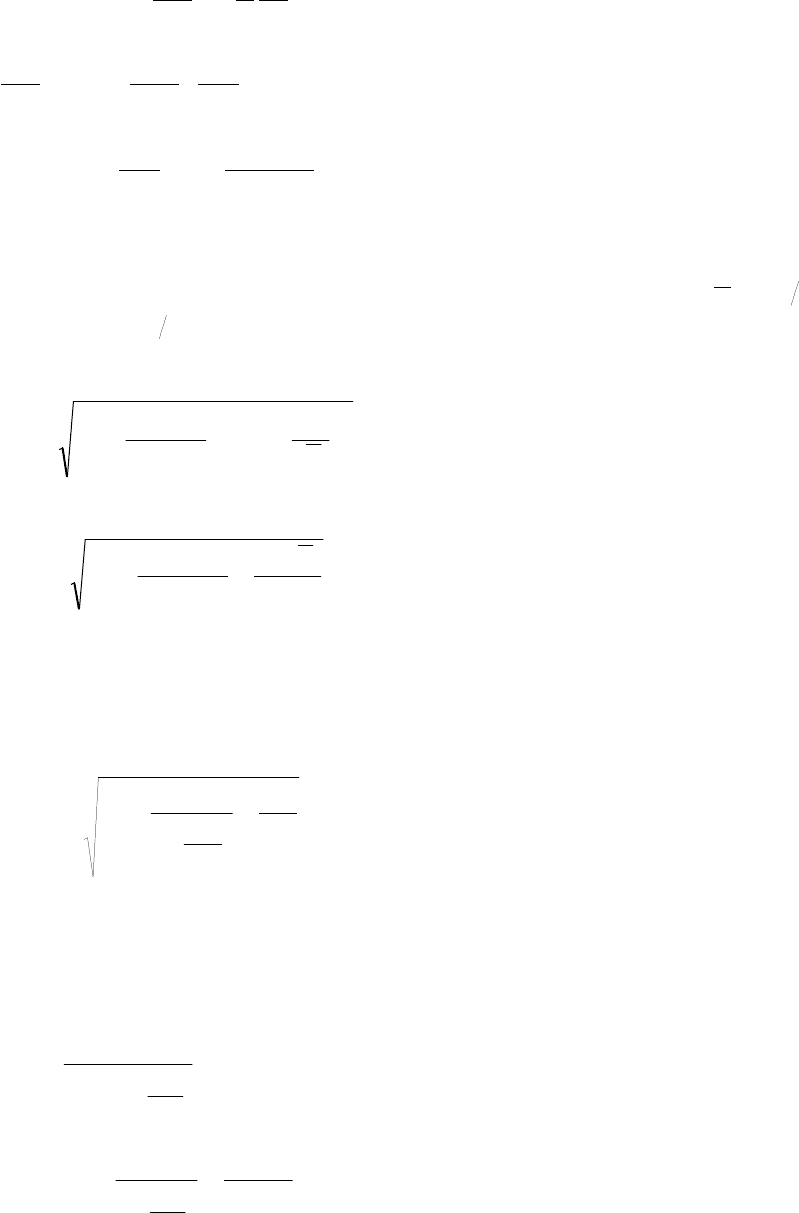
к
РР =
при
>
∞
→
t
r
,
0 (3)
Введем
условие
на
забое
скважины
- Q
ат
= const
массовый
дебит
.
Q
,2 rh
r
Pk
Р
Р
F
ат
ат
т
π
µ
ρ
ϑρ
⋅
∂
∂
⋅⋅=⋅⋅=
.
2
r
P
r
P
kh
Q
Q
ат
ат
ат
т
∂
∂
==
µ
π
ρ
Откуда
kh
РQ
r
P
r
атат
r
π
µ
=
∂
∂
=
0
2
(4)
Проводя
аналогию
между
неустановившейся
фильтрацией
упругой
жидкости
и
идеального
газа
делаем
вывод
,
что
все
соотношения
для
идеального
газа
давление
входит
в
квадрате
,
коэффициент
пьезопроводности
для
жидкости
æ
заменяется
на
mkPæ
к
µ
=
для
газа
,
коэффициент
(
)
(
)
./2 kh
Рна
QkhQ
атат
ππµ
−
В
остальном
все
соотношения
аналогичны
.
Тогда
решение
уравнения
(2)
при
условии
(3)
и
(4)
имеет
вид
( )
.
æ4
2
,
2
2
−−−
t
r
E
kh
РQ
PtrP
i
аат
к
π
µ
(5)
Изменим
давление
на
забое
скважины
(
при
r= r
c
)
( )
2
2
æ25,2
ln
2
c
атат
кc
r
t
kh
РQ
PtP
π
µ
−= (6)
Лекция № 24. Решение задачи о притоке газа к скважине методом ПССС.
В
любой
момент
времени
возмущенной
областью
является
круговая
область
радиусом
r(t)
внутри
которой
давление
распределяется
по
стационарному
закону
:
( )
,
)(
ln
)(
ln
,
22
2
r
tr
r
tr
РР
РtrP
c
ск
к
−
−=
(
)
.trrr
c
≤≤ (1)
Вне возмущенной области
к
РР = при r>r(t). (2)
В возмущенной области принимается
constQ
ат
= при
c
rr = (3)
(
)
( )
c
ат
ск
ат
r
tr
Р
РРkh
Q
ln
22
µ
π
−
= (4)
Из (10.18)
( )
kh
РQ
r
tr
РР
ат
c
ск
π
µ
=
−
ln
22
(5)
Подставив (5) в (1), получим
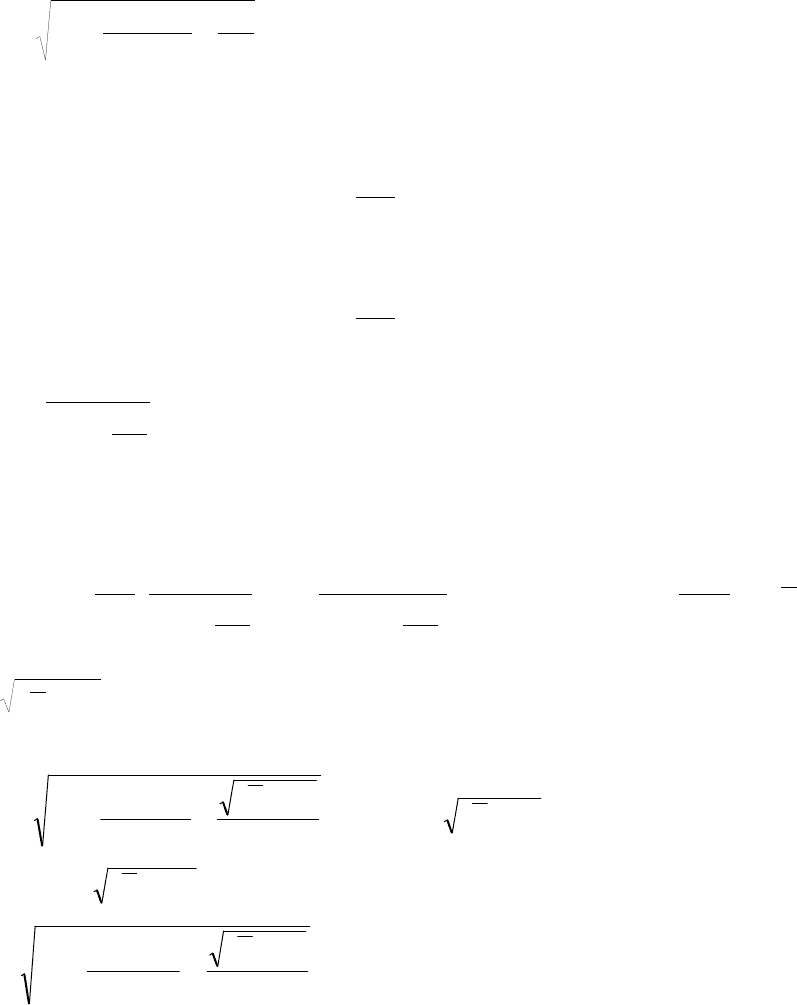
(
)
r
tr
kh
РQ
РtrP
атат
к
ln),(
2
π
µ
−= (6)
Для нахождения r(t) составим уравнение материального баланса.
Начальный запас газа (при
к
PP = ) в зоне радиуса r(t)
( )
[
]
( )
[
]
к
ат
ат
cкc
Р
P
hmrtrhmrtrМ
ρ
πρπ
2222
−=−=
o
(7)
Текущий запас газа
( )
[
]
( )
[
]
Р
Р
hmrtrhmrtrМ
ат
ат
cct
~
22222
ρ
πρπ
−=−= (8)
где
( )
c
к
ск
к
r
tr
Р
РР
РР
ln4
~
22
−
−= (9)
т.к. отбор газа происходит с постоянным дебитом, то ,tQMM
ататt
ρ
=−
o
или с учетом
(10.21), (10,22) и (10.23) находим:
( )
[ ]
( )
(
)
( )
,
lnln4
(
22)22
22
t
r
tr
Р
РРkh
r
tr
Р
РР
Р
hmrtr
c
ат
ск
ат
c
к
ск
ат
ат
c
⋅
−
=
−
⋅−
µ
π
ρ
ρ
π
откуда
( )
tæt
m
kР
rtr
к
c
4
4
22
==−
µ
или
(
)
2
4
c
rtætr += (10)
Подставляя
(10)
в
(6)
получим
( )
,
æ4
ln,
2
2
r
rt
kh
РQ
РtrP
c
атат
к
+
−=
π
µ
,æ4
2
cc
rtrr +≤≤
,
к
РР
=
,æ4
2
c
rtr +>
(11)
( )
c
c
атат
к
c
r
rt
kh
РQ
РtP
2
2
æ4
ln
+
−=
π
µ
(12)
Лекция № 25. Приближенное решение задач об отборе газа из замкнутого пласта.
Пусть
в
центре
замкнутой
круговой
залежи
радиуса
к
r
находится
скважина
радиуса
c
r .
Начальное
пластовое
давление
равно
н
P .
Рассматриваются
два
случая
:
а
)
отбор
производится
с
постоянным
дебитом
ат
Q ;
б
)
забойное
давление
сохраняется
постоянным
.
Обе
задачи
решаются
методом
ПССС
,
т
.
е
.
с
использованием
законов
стационарной
фильтрации
газа
и
уравнения
истощения
залежи
.
Это
последнее
уравнение
–
уравнение
материального
баланса
–
заключается
в
том
,
что
количество
газа
,
извлеченного
из
пласта
за
некоторый
промежуток
времени
,
равно
уменьшению
запасов
газа
в
пласте
,
так
кА
пласт
ограничен
,
то
запасы
ограничены
и
не
пополняются
извне
.
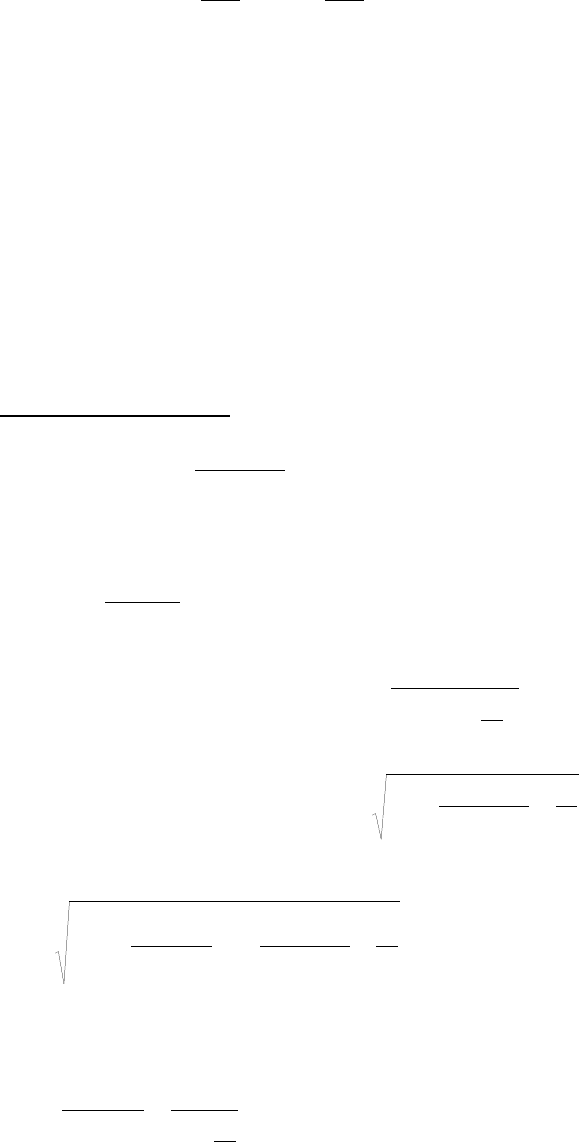
Если
ρ
~
-
плотность
идеального
газа
,
соответствующая
средневзвешенному
давлению
в
пласте
P
~
,
а
пор
V -
объем
порового
пространства
пласта
,
принимаемый
постоянным
,
то
уменьшение
запасов
газа
за
бесконечно
малый
промежуток
времени
запишется
в
виде
:
,
~
22
ρ
ρρ
αρ
dV
Р
Р
Р
VdV
пор
ат
ат
ат
ат
порпор
−=
⋅−=−
(1)
отобранная
масса
газа
за
тот
же
промежуток
времени
(
)
(
)
dttQdttQ
атат
m
ρ
−= (2)
Приравнивая
(1)
и
(2),
получим
дифференциальное
уравнение
истощения
газовой
залежи
:
(
)
dttQPdV
ататпор
=−
2
ρ
(3)
Для
установившейся
плоскорадиальной
фильтрации
газа
P
~
очень
мало
отличается
от
давления
на
границе
замкнутого
пласта
к
Р
.
Поэтому
принимая
к
PP =
,
получим
(
)
dttQ
Р
d
Р
V
ататкпор
=− (4)
Рассмотрим
случай
а
)
когда
constQ
ат
= .
При
этом
dt
V
Q
Р
dP
пор
атат
к
⋅
−= (5)
Интегрируя
(5),
учитывая
,
что
н
РР
=
при
t=0,
получаем
t
V
Q
Р
РР
пор
атат
нк
⋅−= (6)
Из
формулы
дебита
скважины
(
)
c
к
ат
ск
ат
r
r
Р
РР
kh
Q
ln
22
µ
π
−
= (7)
можно
выразить
забойное
давление
:
.ln
2
c
к
атат
к
c
r
r
kh
РQ
PP
π
µ
−=
(8)
С
учетом
(6)
находим
c
к
атат
пор
атат
нс
r
r
kh
РQ
V
tQР
РР ln
2
π
µ
−
−= (9)
В
случае
б
) constP
c
=
для
определения
зависимости
к
Р
от
t
подставим
(7)
в
(4)
и
разделим
переменные
:
dt
r
r
kh
РР
dP
V
c
к
ск
к
пор
ln
22
µ
π
=
−
− (10)
Интегрируя
(10)
от
0
до
t
и
от
н
Р
до
к
Р
,
получим

( )
( )( )
( )( )
сксн
сксн
c
c
к
cк
РРРР
РРРР
kP
r
r
rrm
t
−+
+−
−
= ln
2
ln
22
µ
(11)
Лекции № 26, 27. Взаимное вытеснение жидкостей
Задачи
о
движении
границы
раздела
дух
жидкостей
в
пористой
среде
представляют
большой
теоретический
и
практический
интерес
.
При
разработке
нефтяных
месторождений
в
условиях
водонапорного
режима
наблюдается
стягивание
контура
нефтеносности
(
КН
)
под
напором
краевой
воды
.
1.
Кинематические
условия
на
подвижной
границе
раздела
при
взаимном
вытеснении
жидкостей
.
B
A
Основная
трудность
точного
решения
задачи
о
движении
границы
раздела
двух
жидкостей
в
пористой
среде
заключается
в
том
,
что
линии
тока
на
границе
раздела
жидкостей
преломляются
.
Пусть
кривая
I-I (
рис
. 1)
является
границей
раздела
двух
жидкостей
с
вязкостями
1
µ
и
2
µ
,
и
пусть
,
например
,
2
µ
>
1
µ
(
нефть
вытесняется
водой
).
Рссмотрим
произвольную
точку
М
границы
I-I
и
проведем
через
нее
касательную
τ
r
и
нормаль
n
r
к
грнице
раздела
жидкостей
I-
I.
Найдем
проекции
скоростей
фильтрации
воды
и
нефти
,
находящихся
в
данный
момент
в
точке
М
,
еа
касательную
τ
r
и
нормаль
n
r
считая
проницаемость
пористой
среды
k
постоянной
по
обе
стороны
границы
раздела
.
Согласно
условию
неразрывности
потока
массы
элементарные
расходы
обеих
несжимаемых
жидкостей
через
элемент
границы
раздела
,
включающий
точку
М
,
должны
быть
равны
между
собой
.
Отсюда
следует
,
что
нормальные
составляющие
скоростей
фильтрации
обеих
жидкостей
будут
равны
,
т
.
е
.
nn 21
ϑϑ
= .
Давление
в
пласте
в
точке
М
также
должно
быть
одинаково
для
обеих
жидкостей
,
так
как
при
малых
скоростях
(
ниже
звуковых
)
разрыва
давления
в
сплошном
потоке
быть
не
может
.
Касательные
составляющие
скоростей
фильтрации
обеих
жидкостей
будут
определяться
по
закону
Дарси
:
;
1
1
τµ
ϑ
τ
∂
∂
−=
Pk
(1)
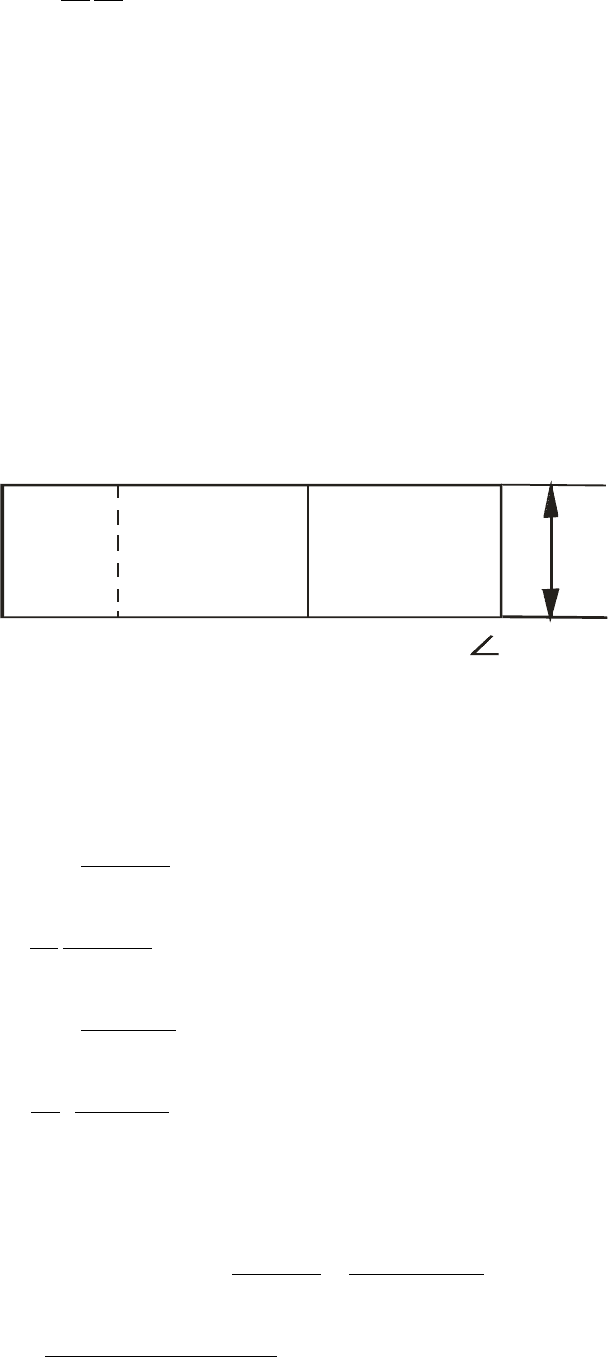
;
2
2
τµ
ϑ
τ
∂
∂
−=
Pk
(2)
Так
как
2
µ
>
1
µ
,
то
из
(1)
и
(2)
получаем
,
что
ττ
ωω
21
> .
Отсюда
следует
,
что
результирующий
вектор
скорости
фильтрации
(
)
,
1111 n
ϑϑϑϑ
τ
r
r
r
r
+=
касательный
к
линии
тока
АМ
,
будет
больше
вектора
(
)
n2222
ϑϑϑϑ
τ
r
r
r
r
+= ,
касательного
к
линии
тока
нефти
МВ
.
Следовательно
,
линии
тока
АМ
и
МВ
,
проходяшие
через
точку
М
,
будут
иметь
излом
в
точке
М
.
Учет
этого
преломления
линий
тока
на
границе
раздела
жидкостей
и
составляет
главную
трудность
в
точном
решении
задачи
продвижения
границы
раздела
.
Лини
тока
не
будут
преломляться
только
в
двух
случаях
–
при
прямолинейно
-
паралельном
и
плоскорадиальном
движениях
границы
раздела
,
когда
.0
21
==
ττ
ϑϑ
Эти
задачи
прежде
всего
и
будут
рассмотрены
в
данной
главе
.
При
этом
жидкости
(
нефть
и
вода
)
считаются
несжимаемыми
,
взаимно
нерастворимыми
и
химически
не
реагирующими
одна
с
другой
и
с
пористой
средой
.
Вытеснение
нефти
водой
предполагается
происходящим
полностью
–
так
называемое
поршневое
вытеснение
.
2.
Прямолинейно
-
параллельное
вытеснение
нефти
водой
(
рис
. 2)
X
O
O
P(t)
X t)в(
B
P
K
K
к
РР =
при
x=0;
г
РР =
при
x=L;
−
o
x
начальное
положение
ВНК
.
(
)
−tx
в
текущее
положение
.
Примем
,
вн
ρρ
=
т
.
е
.
граница
нефть
-
вода
–
вертикальная
.
Распределение
давления
и
скорость
фильтрации
в
водоносной
и
нефтеносной
областях
:
(
)
( )
,x
tx
tРР
РР
в
к
кв
⋅
−
−=
0
(
)
,txx
в
≤≤ (3)
(
)
( )
,
tx
tРР
k
в
к
в
в
−
=
µ
ϑ
(4)
(
)
( )
[ ]
,хL
tхL
РtР
РР
к
вк
г
гн
−
−
−
+=
(
)
,
кв
Lxtх ≤≤ (5)
(
)
( )
.
tхL
РtР
k
вк
г
н
н
−
−
⋅=
µ
ϑ
(6)
Из
условия
,
что
нв
ϑϑ
=
имеем
(
)
( )
(
)
( )( )
,
tхL
РtР
tх
tРР
вкн
г
вв
к
−
−
=
−
µµ
откуда
( )
(
)
( )
вввкн
ввгвкнк
ххL
хРхLР
tP
µµ
µµ
+−
+−
=
(7)
Подставляя
(7)
в
(3)-(6),
получим
(
)
( )
,х
хLх
РР
РР
вкнвв
гкв
кв
⋅
−+
−
−=
µµ
µ
(8)
(
)
( )
( )
,хL
хLх
РР
РР
к
вкнвв
гкн
гн
−
−+
−
+=
µµ
µ
(9)
(
)
( )
вкнвв
гк
нв
хLх
РРk
−+
−
==
µµ
ϑϑ
, (10)
Далее
(
)
( )
вкнвв
гк
хLх
РРBkh
BhQ
−+
−
=⋅=
µµ
ϑ
, (11)
Закон
движения
границы
раздела
определяется
из
выражения
,
dt
dx
m
W
в
==
ϑ
откуда
( )
( )
[ ]
ввкнвв
гк
в
dxхLх
РРk
m
dx
m
dt −+
−
==
µµ
ϑ
(12)
интегрируя
(12)
в
пределах
от
0
до
t
и
от
o
x
до
в
x ,
получим
( )
( )( )
−
−−+
−
−
=
22
2222
o
o
o
хх
ххL
хх
РРk
m
t
в
нвкн
в
в
гк
µµµ
( )
( ) ( )
−+−
−
−
−
=
o
o
ххL
хх
РРk
m
t
вкнвн
в
гк
µµµ
2
22
(13)
Время
полного
вытеснения
нефти
водой
определяется
из
(13)
при
,
кв
Lх =
т
.
е
.
( )
(
)
( )
[
]
2
22
2
oo
хLхL
РРk
m
T
кнкв
гк
−+−
−
=
µµ
(14)
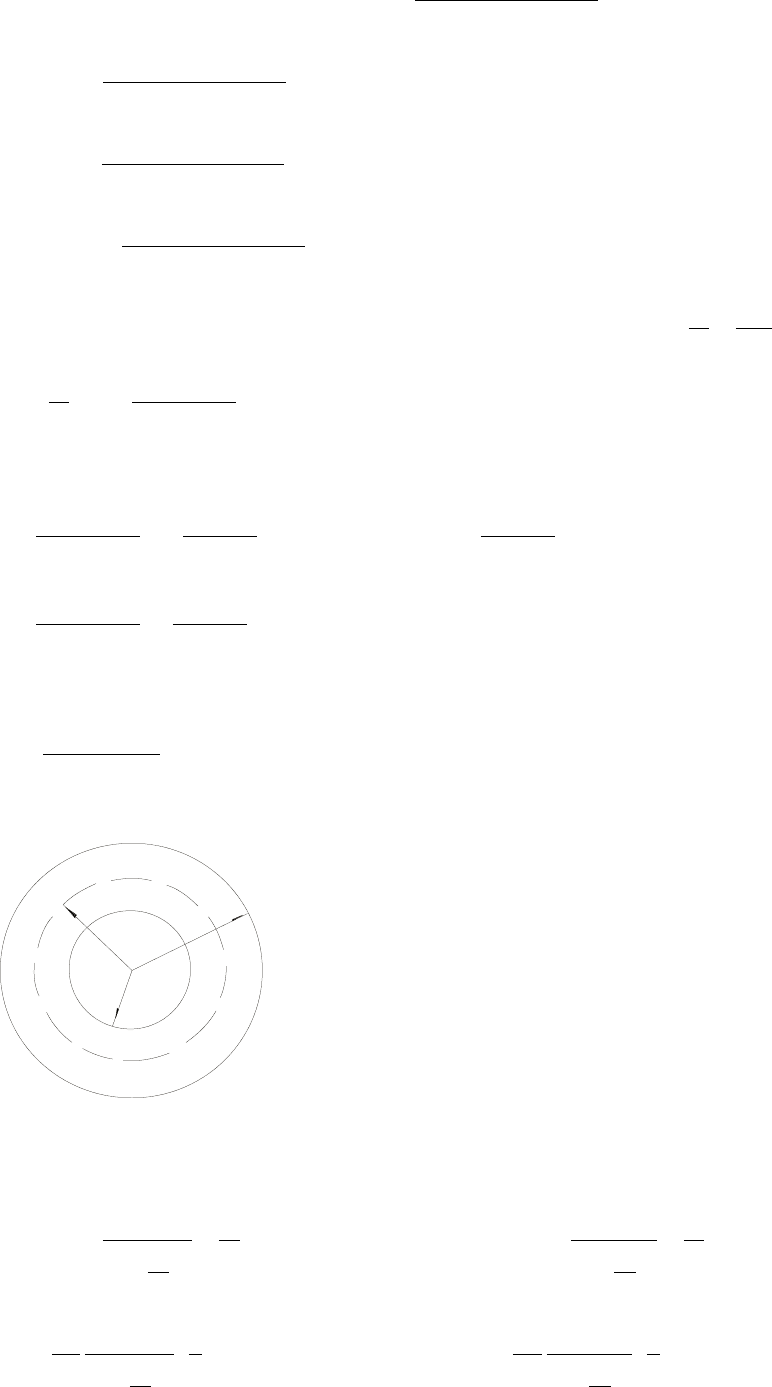
2.
Плоскорадиальное
вытеснение
нефти
водой
(
рис
. 3)
−
o
r
радиус
начального
положения
ВНК
;
−
н
r
радиус
текущего
положения
ВНК
;
−
к
r
радиус
КП
; −
c
r
радиус
скважины
.
(
)
,ln
ln
r
r
r
r
tРР
РР
к
н
к
к
кв
−
−= (15)
(
)
,ln
ln
c
c
н
c
сн
r
r
r
r
PtР
РР
−
+= (16)
(
)
,
1
ln
r
r
r
tРР
k
н
к
к
в
в
⋅
−
=
µ
ϑ
(17)
(
)
.
1
ln
r
r
r
PtР
k
с
н
c
н
н
⋅
−
=
µ
ϑ
(18)
При
н
rr = ,
нв
ϑϑ
=
т
.
е
.
(
)
(
)
c
н
н
c
н
к
в
к
r
r
PtР
r
r
tРР
lnln
µµ
−
=
−
откуда
( )
н
к
в
с
н
н
н
к
вс
с
н
нк
r
r
r
r
r
r
Р
r
r
Р
tP
lnln
lnln
µµ
µµ
+
+
= (19)
Подставляя
(19)
в
(15)-(18),
получим
:
(
)
,ln
lnln
r
r
r
r
r
r
РР
РР
к
с
н
н
н
к
в
скв
кв
µµ
µ
+
−
−= (20)
(
)
,ln
lnln
c
c
н
н
н
к
в
скн
сн
r
r
r
r
r
r
РР
РР
µµ
µ
+
−
+= (21)
(
)
,
1
lnln
r
r
r
r
r
РРk
c
н
н
н
к
в
ск
⋅
+
−
=
µµ
ϑ
(22)
(
)
.
lnln
2
c
н
н
н
к
в
ск
r
r
r
r
РРkh
Q
µµ
π
+
−
= (23)
Закон
движения
границы
раздела
жидкостей
:
dt
dr
m
W
н
−==
ϑ
или
( )
нн
c
н
н
н
к
в
ск
drr
r
r
r
r
РPk
m
dt
+
−
−= lnln
µµ
(24)
интегрируя
(24)
в
пределах
от
0
до
t
и
от
r
до
н
r ,
получим
:
( )
( )
−
−
−
−+
−
−
=
222222
2
lnlnlnln
2
н
вн
н
к
н
к
d
c
н
н
c
н
ск
rr
r
r
r
r
r
r
r
r
r
r
r
r
РРk
m
t
o
o
o
o
o
µµ
µµ
(25)
Время
полного
вытеснения
нефти
водой
Т
определяется
из
(25)
при
.
cн
rr =
Принебрегая
2
c
r
по
сравнению
с
2
o
r ,
получим
:
( )
++
−⋅
−
=
rr
r
r
rr
r
r
РРk
m
T
к
в
c
н
ск
1
ln
1
ln
2
22
o
o
o
o
µµ
(26)
Лекция № 28. Двухфазное течение несмешивающихся жидкостей.
Теория Баклея-Леверетта
Добыча
нефти
в
большинстве
случаев
происходит
при
замещении
ее
в
поровом
пространстве
продуктивного
пласта
водой
или
газом
.
Взаимодействие
пластовых
флюидов
между
собой
и
с
пористой
неоднородной
структурой
обуславливает
капиллярные
явления
,
неполное
и
неравномерное
вытеснение
,
образование
в
пласте
зон
совместного
течения
флюидов
.
Как
только
начинается
движение
контура
нефтеносности
(
КН
),
в
пласте
возникает
область
между
первоначальным
положением
КН
и
его
положением
в
данный
момент
времени
,
в
которой
,
кроме
вторгшейся
воды
,
содержится
еще
остаточная
нефть
.
При
движении
смеси
двух
фаз
возникает
капиллярный
эффект
.
Для
одной
и
той
же
точки
фильтрующей
среды
давления
воды
не
равны
друг
другу
.
Разность
их
есть
капиллярное
давление
.
В
практических
расчетах
для
однородного
пласта
капиллярное
давление
можно
не
учитывать
,
так
как
можно
считать
,
что
капиллярный
эффект
учитывается
кривыми
фазовых
проницаемостей
.
Суммарная
скорость
фильтрации
смеси
ϑ
записывается
так
:
dP
kk
r
н
н
в
в
∫
+
∂
∂
=
µµ
ϑ
(1)
Пусть
движение
прямолинейно
-
параллельное
,
а
жидкость
несжимаема
.
Подставим
(1)
в
уравнение
неразрывности
:
=
+
∂
∂
∂
∂
∫
dP
kk
xx
н
н
в
в
µµ
0 (2)
где
х
заменяет
основную
координату
r.
Из
(2)
следует
,
что
суммарная
скорость
фильтрации
неизменна
вдоль
оси
ОХ
const
x
Р
kk
н
н
в
в
=
∂
∂
+−=
µµ
ϑ
(3)
Найдя
из
(3)
значение
,xP ∂∂
подставим
его
в
выражение
скорости
фильтрации
для
воды
в
ϑ
:
( )
,sf
kk
k
х
Р
k
н
н
в
в
вв
в
в
в
⋅=
+
=
∂
∂
−=
ϑ
µµ
µ
ϑ
µ
ϑ
(4)
где
( )
−
+
=
н
н
в
в
вв
kk
k
sf
µµ
µ
функция
С
.
Ф
.
Баклея
и
М
.
С
.
Леверетта
;
s –
водонасыщенность
.
Составим
уравнение
неразрывности
для
воды
:
.
t
s
m
x
в
∂
∂
−=
∂
∂
ϑ
(5)
Дифференцируя
(4)
по
х
и
подставляя
результат
в
(5),
получим
:
(
)
=
∂
∂
+
∂
∂
⋅
∂
∂
⋅
t
s
m
x
s
s
sf
ϑ
0 (6)
Вычислим
полную
производную
от
S
по
времени
:
.
t
s
t
x
x
s
dt
ds
∂
∂
+
∂
∂
⋅
∂
∂
= (7)

из
(7)
найдем
t
s
∂
∂
и
подставим
его
в
(6).
Для
плоскости
,
в
которой
насыщенность
S
сохраняет
постоянное
значение
,
=dtds
0;
следовательно
,
из
(6)
и
(7)
получим
уравнение
:
(
)
ds
sdf
m
dt
dx
⋅=
ϑ
(8)
Уравнение
(8)
называется
уравнением
Баклея
-
Леверетта
,
которое
позволяет
определить
скорость
распределения
заданной
насыщенности
S.
Проинтегрировав
(8)
по
t,
найдем
(
)
ds
sdf
m
t
xx ⋅
⋅
=−
ϑ
o
(9)
где
х
и
o
x
-
координаты
рассматриваемой
плоскости
в
моменты
времени
t
и
0;
−
t
ϑ
полный
объем
жидкости
,
отнесенный
к
единице
площади
поперечного
сечения
,
вторгшейся
в
данную
область
за
время
t.
Лекция № 29, 30. Особенности фильтрации в трещиноватых и трещиновато-пористых
пластах
Рассматривается
две
модели
пород
:
чисто
трещиноватые
и
трещиновато
-
пористые
.
В
трещиноватых
породах
блоки
породы
,
расположены
между
трещинами
,
практически
непроницаемы
;
движение
жидкости
и
газа
происходит
только
по
трещинам
.
К
таким
породам
относятся
сланцы
,
доломиты
,
мергели
и
некоторые
известняки
.
Трещиновато
-
пористая
среда
представляет
собой
совокупность
пористых
блоков
,
отделенной
друг
от
друга
развитой
системой
трещин
.
При
этом
поперечные
размеры
трещин
значительно
превосходят
характерные
размеры
пор
,
так
что
проницаемость
систем
трещин
1
k
значительно
больше
проницаемости
системы
пор
в
блоке
2
k
.
В
то
же
время
трещины
занимают
гораздо
меньший
объем
,
чем
поры
,
так
что
коэффициент
трещиноватости
1
m
-
отношение
объема
,
занятого
трещинами
,
к
общему
объему
породы
–
существенно
меньше
пористости
отдельных
блоков
2
m
.
Трещиновато
-
пористые
коллекторы
–
это
,
в
основном
известняки
,
иногда
песчаники
,
алевролиты
,
доломиты
.
Важным
параметром
трещиноватой
среды
является
густота
трещин
-
отношение
числа
трещин
секущих
нормаль
,
к
длине
нормали
,
приведенной
к
поверхности
,
образующей
трещины
:
hnГ =
.
Если
трещиноватый
пласт
моделируется
одной
сеткой
горизонтальных
трещин
,
причем
все
трещины
одинаково
раскрыты
и
равно
отстоят
друг
о
друга
,
то
густота
их
–
число
трещин
,
приходящееся
на
еденицу
толщины
пласта
(
)
hnГ =
.
Тогда
коэффициент
трещиноватости
δ
δ
⋅== Г
ach
nac
m
1
,
где
δ
-
раскрытие
трещины
.
Если
в
пласте
имеются
две
взаимноперпендикулярные
системы
трещин
с
одинаковой
густотой
и
раскрытием
,
то
δ
Гm 2
1
=
,
если
системы
три
,
то
δ
Гm 3
1
=
.
В
общем
случае
:
δθ
Гm =
1
(1)
где
θ
-
безразмерный
коэффициент
,
зависящий
от
геометрии
систем
трещин
в
породе
.
Проницаемость
трещиноватой
породы
k,
определяется
по
зависимости
:

(
)
[
]
3
11
1 РРkk
т
−−=
o
o
β
, (2)
где
12
3
1 o
o
δθ
Гk = ,
т
β
-
параметр
трещиноватой
среды
,
зависящий
от
упругих
свойств
и
геометрии
трещин
.
Экспериментально
хорошо
подтверждается
экспоненциальная
зависимость
проницаемости
от
давления
:
(
)
PP
ekk
−−
=
o
o
α
11
, (3)
а
при
малых
изменениях
давления
:
(
)
[
]
PPkk −−=
o
o
α
1
11
,
где
т
βα
3= (4)
Используя
обычную
теорию
фильтрации
упругой
жидкости
,
определим
коэффициент
пьезопроводности
трещиноватой
среды
(
)
[
]
,/æ
111 сж
mk
ββµ
+=
который
может
оказаться
слишком
большим
,
т
.
к
.
1
k
велик
,
а
1
m
-
мал
.
Это
значит
,
что
перераспределение
давления
в
трещинах
будет
происходить
с
большей
скоростью
.
Из
-
за
малой
проницаемости
блоков
2
k
,
жидкость
из
них
выходит
медленно
и
давление
в
блоках
длительное
время
сохраняет
свое
начальное
давление
.
Тем
самым
между
жидкостью
,
находящейся
в
блоках
,
и
жидкостью
ее
окружающей
создается
разность
давлений
,
в
результате
чего
происходит
переток
части
жидкости
из
блоков
в
трещины
и
происходит
постепенное
выравнивание
давлений
.
Переток
определяется
по
формуле
:
( )
12
PPq −=
µ
ρ
α
o
o
, (5)
где
2
2
l
k
α
α
=
o
,
o
α
-
безразмерный
коэффициент
,
зависящий
от
геометрических
характеристик
пласта
; l –
средний
размер
блоков
.
Для
идеального
газа
(
)
,
2
2
1
2
2
o
o
o
P
PP
q
µ
ρ
α
−
= (6)
где
o
P
-
давление
,
соответствующее
плотности
o
ρ
.
Дифференциальные уравнения движения жидкости и газа в трещиноватых трещиновато-
пористых средах. (Т и ТПС)
При
составлении
дифференциальных
уравнений
записываются
два
уравнения
неразрывности
–
одно
для
фильтрации
в
трещинах
(
среда
1),
другое
для
фильтрации
в
пористых
блоках
(
среда
2)
с
учетом
перетоков
(q):
Для
фильтрации
в
трещинах
:
(
)
(
)
(
)
(
)
1
11
1
1
q
t
m
zyx
z
y
x
−
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
−
ρρϑ
ρϑ
ρϑ
(7)
где
−
ρ
плотность
жидкости
или
газа
при
давлении
1
P
.
Для
пористых
блоков
:
(
)
(
)
(
)
(
)
,
2
q
t
m
zyx
zz
zy
zx
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
−
ρρϑ
ρϑ
ρϑ
(8)
где
−
ρ
плотность
жидкости
или
газа
при
давлении
2
P
.
Для
чисто
трещиноватых
пластов
q=0
и
остается
только
уравнение
(7).
Дифференциальные
уравнения
движения
в
системе
трещин
и
пористых
блоках
соответственно
имеют
вид
:
,
11
1
x
Pk
x
∂
∂
−=
µ
ϑ
,
11
1
y
Pk
y
∂
∂
−=
µ
ϑ
,
11
1
z
Pk
z
∂
∂
−=
µ
ϑ
(9)
