?tekauer Pavol, Lieber Rochelle. Handbook of Word-Formation

Подождите немного. Документ загружается.

300

PETER A

KEMA

AD NEELEMAN

structure). The only potential competitor left

for (21b) then is (24b). According to

resnan, this structure does not actually have the right semantics to be in

etition with

ren’t I working

as the scope of negation is limited to the VP in

(24b), while the interpretation we are interested in involves sentential negation.

(24) a. *Am not I working

b. Am I not workin

The situation a

ain lends itself well to an OT-anal

sis, b

usin

two Parse-t

traint

in a

iti

n t

amn’t

(which might follow from some more

eneral phonological constraint, a

issue we will ignore here)

The analysis is in the

ame spirit as Bresnan’s, although different in execution.

Following Bresnan, we assume that there

s a constraint according to which the

emantic scope of negation must be mirror

d by overt syntax (say NegScope). For

onstituent negation, this means that the

egator should appear ad

oined to the

onstituent in question; for sentential ne

ation, this constraint demands that the

ator must appear as hi

h in the clause as possible (the more structure dominates

the sentential ne

ator, the more this constraint is violated). In ne

ated declaratives,

andidates with affixal negation (such as

aren’t working) are as good on this

traint a

not

is adjoined to VP (such as

I’m not workin

)

, as

n both cases the amount of structure dominating the negator is the same (the

pro

ections of Infl and higher). In nega

ed interrogatives, candidates with affixal

egation score better on NegScope than candidates with

howeve

Thi

because full ne

ation must be stranded under verb movement to C

(

not

does not

form a constituent with the verb, but is ad

oined to VP), while affixal ne

ation is

taken alon

, thereb

endin

up bein

dominated b

less structure than its

not

rival in

thi

se.

r r

ant

traint i

familiar fr

sec

n 2

it i

eco

traint that

uires

hi-features in the input to be properly realized. As will be clear, sentences

ith

am not

are a better spell out of ‘first-person negative

’

than

ces w

ith

ore general

en’t

The data from (standard) English descri

bed

bove

fall

t fr

m th

eco

traint

ankin

*Amn’t >> Ne

Scope >> ParsePhi, as the followin

tables demonstrate:

<declarative> *Amn’t NegScope ParsePhi

I [amn’t] working *!

)

am [not workin

]

I [aren’t] working

ORD

FORMATION IN OPTIMALITY THEORY

301

<interro

ative> *Amn’t Ne

Scope ParsePhi

[

Amn’t] I working *!

Am I [not working] *

)

[aren’t] I workin

that

Am I not working

is not ungrammatical. Although it cannot express

entential ne

ation, it is the optimal candidate for constituent ne

ation of

orkin

3.2 Competition between modul

es that does not involve the Elsewhere Principle

n the previous subsection we discussed how Elsewhere-style competition can

apply across components. In the current

ubsection we will discuss the possibility

that morphology and syntax compete in the generation of structure, even if the

Elsewhere Principle does not apply. In particular we will make a case for the ide

that when a s

ntactic phrase and a morpholo

ical construct can express the same

nput equall

well, the s

ntactic option blocks the morpholo

ical one, at least in

es like En

lish

onsider the way in which the semantic relation between a predicate and its

direct argument can be realized structu

ally. One obvious possibility is to combine

them syntactically, giving rise in the case of a verb to a standard transitive verb

phrase. A perhaps less obvious, but logically equally available, option is to form a

oot compound. After all, the semantic relation between the two members of a root

ompound is not inherentl

restricted, and could therefore subsume the predicate-

ument relation. It is, therefore, surprisin

that this t

pe of root compound is

stematicall

absent. The VP in (25a) does not alternate with the N-V compound in

(

25b

(

)

a. to [

drive

[

trucks

]]

b. *to

[

truck

]

The pattern is more general: root compounds in general cannot have a

trans

arent semantics. Thus, the structure of

renominal modification in Dutch

(

26a

)

does not alternate with the A-N com

ound in

(

26b

)

(

)

a. [

[

blauwe] ogen

]

blue-

eyes

[

oge

]

This cannot be due to a lack of N-V compounding in English or A-N

ompounding in Dutch. Both are in fact fairly productive. (27) and (28) give lists of

examples that can easil

be extended.

An extended version of the argument can be found in Ackema & Neeleman (2004).

2 PETER A

KEMA

D NEELEMAN

These examples show that the semantics of root compounds varies wildl

, but in

o case does the com

ound have a tra

arent com

ositional semantics.

nterestin

, ar

ument-predicate relati

nshi

s and trans

arent modifier-head

elationshi

can

sometimes hold between parts of words. In particular, synthetic

ounds can ex

ress such relationshi

s as a matter of course

(

)

[

truck

] er

]

[

] i

]

lue e

e ed

This state of affairs can explained in terms of competition between s

ntax and

orphology on the following assumption:

(30) Syntactic merger of (a projection of)

and (a projection of)

orphological merger if the semantic relation between

ide

nti

al in th

wo c

ses.

(

30) immediatel

explains wh

morpholo

ical mer

er of a verb and its direct

ect is blocked: a s

ntactic competitor is alwa

s available. The same holds of

tructures of prenominal modification.

t the same time, the synthetic compound in (31a) is allowed to coexist with its

yntactic counterpart in (31b). The point is that in (31b)

uck

merges with a

projection of -

while in (31a) it merges with a projection of

ive

. As a result

one

annot say that (pro

ections of) the same categories merge in the two cases in (31).

Hence, given (30), competition does not obtain.

(

)

[

truck

] er

]

The argument given in this section relies on the str

ture of synthetic compounds being as indicated in

(

29). For argumentation that the alternative right-b

anching structure cannot express the meaning of a

ynthetic compound, see Ackema & Neeleman (2004).

(27) to breast-feed to hand-make to bab

-sit

to pla

-act to air-condition to bar-tend

to window-shop to c-command to pressure-clean

to base-generate to c

omsky-adjoin to pan-fry

to head-adjoin to head-govern to carbon-date

(28) zoet-hout speciaal-zaak

weet-wood special

hop

‘liquorice’ ‘specialist shop’

art-

boe

in-

black-book

rown-

ish

‘blackbook’ ‘

oise’

ORD

FORMATION IN OPTIMALITY THEORY

303

[

]

(

)

[

trucks

]]

his result crucially relies on -

being a projecting affix, that is, an affix that is

the head of the morpholo

ical complex it derives. Of course, we can also combine

ive

with an affix and pro

ect

ive

rather than the affix.

n such a case s

nthetic

ompoundin

is predicted to be impossible, since

uck

now again merges with a

projection of

ive

just as in the syntactic competito

. Therefore,

(

32a

)

blocks

(

32b

)

(

)

a. John [

[

]

[

trucks

]]

b. *John

[

truck

]

he nontransparent root compounds in (27) and (28) are grammatical, as they do

ot have a s

ntactic counterpart in which the same pro

ections mer

e either. To

ive

an exam

le, to pan-

does not mean the same thin

as to

pans

but rather the

ame thin

as to

in a pan. But in the latter case

mer

es with a pro

ection o

the

osition

and not with a projection of the noun

an. This syntactic phrase is

therefore not in com

etition with to pan-fr

he kind of competition characterized by (30) can trivially be modelled in OT.

he account would be based on two constraints, namely more specific instantiations

f the more general *Struc (see section 2.3): *MorphStruc and *SynStruc, which

ilitate a

ainst morpholo

ical and s

ntactic structure, respectivel

. In En

lish the

former must outrank the latter. It is, at this

oint, an o

uestion whether these

onstraints are rerankable. Possibl

, r

kin

nStruc above *MorphStruc

ives

ise to polysynthetic languages.

. COMPETITION BETWEEN DIFFERENT MORPHEME ORDERS

he examples of purely morphological co

petition discussed in section 2 all

nvolve candidates that differ in the morphemes they use to spell out a

orphosyntactic input. In this section w

consider cases of competition in which

andidates differ not in the morphemes they contain, but rather in the order in which

these mor

hemes show u

s a point of departure we ma

take a constraint that disfavors ‘crossin

orrespondences’ between morphos

ntactic and morphophonolo

ical structures (see

Marantz 1984 and Sproat 1985). In derivational morphology, for example, there

usually is a one-to-one, left

to-right mapping of morpho

yntactic positions to the

phonemes that realize them. Thus, an input like (33a) (with the semantics

‘something that is like a mini computer’) is realized as in (33b), not as in (33c). An

nput like (34a) (with the semantics of ‘something small that is like a computer’) is

ealized as

(

34c

)

, rather than

(

34b

)

(

)

a. [

[

MINI

TER

]]

b. /

seudo/ /mini/ /com

uter

c. */mini/ /

seudo/ /com

uter

304

PETER A

KEMA

AD NEELEMAN

(

)

a. [

MINI

[

PSE

DO COMP

TER

]]

b. */

seudo/ /mini/ /com

uter/

c. /mini/ /

seudo/ /com

uter

he constraint regulating this mirroring effect (compare Baker 1985) can be

formulated as in (35) (adapted from Sproat 1985: 82). (As in (33) and (34),

orphos

ntactic positions are repre

ented in capitals, while correspondin

orphophonolo

ical units appear in lower case and between slashes.) Note that

ith

t Linear Corres

ondence

random affix orderin

would be the norm.

(

)

Linear Corres

ondenc

If X is structurally external to Y,

X is phonologically realized as /x/, and

Y is phonologically realized as /y/

then /x/ is linearly external to /y/.

4.1 Conflicts between Linear Corr

pondence and templatic requirements

he constraint in (35) may seem trivial. But it turns out that there can be

onflicting constraints on affix ordering that lead to a non-transparent ordering of

orphemes. An instance of this is discussed by Hyman (2003). It concerns the

rdering of certain postverbal affixes in Bantu languages, namely those affixes that

express operations that change argument structure. Consider combinations of

ausative and applicative morpholo

(the applicative marks an operation b

which

nstruments and the like are

romoted

o direct ar

ument). Presumabl

, the

orphos

ntactic structures of a causative applicative and an applicative causative

are distinct

with the causative affix c-

ommanding the applicative affix in the

former, while being c-commanded by the applicative affix in the latter. Linear

orrespondence requires that these structural relations are reflected by morpheme

rder in the morphophonology:

(

)

a. [[V

APPLICATIV

]

SATIV

]

b. [[/v/-/applicative/]-/causative/]

(

)

a. [[V

ATI

]

PPLI

ATI

]

b. [[/v/-/causative/]-/a

licative/]

here are various languages that are well behaved in this respect, so that the

applicative and causative markers used to express sentences like ‘he made the

hildren cry with a stick’ (with

stick

being promoted to direct argument by

applicative) and ‘he made the children stir with a spoon’ (with

poon being

promoted to direct ar

ument b

applicative), respectivel

, show up in different

rders, as in the former applicative has applied to an instrument of causation (i.e.

licative a

lies after causativization

)

, while in the latter it has a

lied to an

stir

(i.e. applicative applies before causativization). Surprisingly,

ORD

FORMATION IN OPTIMALITY THEORY

305

owever, one can also find languages that use the same morpheme order to express

the structures in (36a) and (36b). Consider the following data from Chichewa (see

Hyman 2003; for general discussion of Ch

chewa morpheme order, see Hyman &

Mchombo 1992

)

(

38) a. Alen

é a-ku-líl

-il

a m

aná n

dodo

hunte

PRO

-cry

CAUSE

APPL

child sticks

‘The hunters are making the child cry with sticks’

b. Alenjé a-ku-tákás-it

-il

a mkází mthík

hunte

sti

APPL

woman spoon

‘The hunters are making the woman stir with a spoon’

oth the a

licativized causative in

(

38a

)

and the causativized a

licative in

(

38b

)

have the same order of the

íts

(

causative

)

and

íl

(applicative) affixes.

ccordin

to Linear Correspondence, the order should be reversed in (38b).

pparently, there is a constraint that overrules Linear Correspondence in this

example. Hyman argues that all Bantu languages want their postverbal derivational

orphemes to occur in a specific order, expressed by the following template:

(

)

an-Bantu Templat

(

CARP

)

Causative-A

licati

e-Reci

rocal-Passive

is ranked above Linear Corres

ondence, a violation of the mirro

rinci

le can result:

[[V

APPLICATIV

]

SATIV

]

> CARP Linear Correspondence

[[/v/-/a

licative/]-/causative/] *!

)

[[/v/-/causative/]-/a

licative/] *

Reranking the two constraints leads to instances where the tem

rifi

ced

n order to express the scopal relation between the morphemes overtly:

[[V

APPLI

ATI

]

ATI

]

> Linear Corres

ondence CARP

)

[[/v/-/a

licative/]-/causative/

]

[[/v/-/causative/]-/applicative/] *!

here is, indeed, language variation in Bantu concerning the extent to which the

template is adhered to. This is not a matter of either followin

the template

ompletel

, or compl

with Linear Correspondence completel

. Within a sin

e, the choice made can differ for an

ndividual

air of derivational affixes.

For example, whereas the order of a

pplicative and causative morphemes in

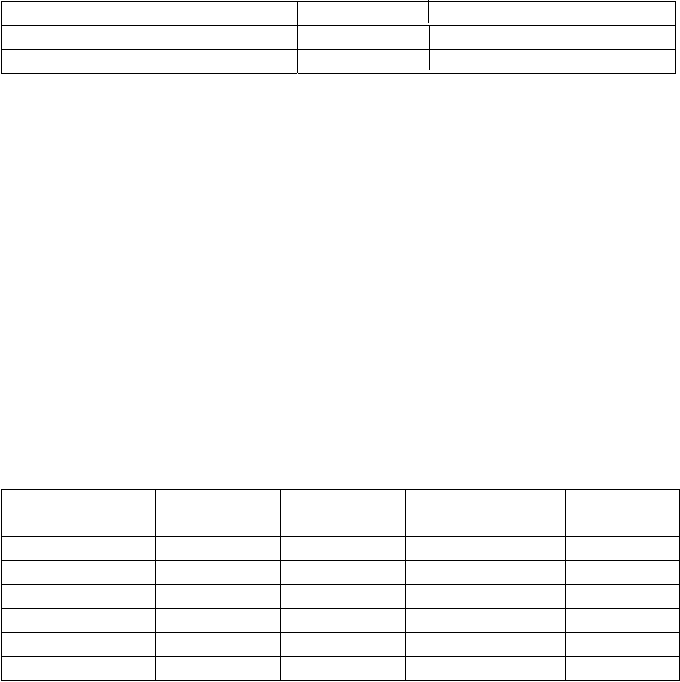
306

PETER A

KEMA

D NEELEMAN

hichewa adheres to the

ARP tem

late, the order between a

licative and

assive

orphemes is determined by Linear Correspondence, with the consequence that in

an a

licativized

assive, the

ostverbal

ARP template is violated. This type of

ariation requires that either the templat

or Linear Correspondence is split into a

family of constraints mentioning pairs of

morphemes. Hyman chooses to split his

ersion of Linear Correspondence in this fashion, since in his view violations of the

late are the exce

tion, rather

han the rule

(

but see below

)

n OT-t

pe anal

sis alon

these lines makes two predictions. The first is that,

althou

h violations of Linear Correspondence are possible, the

are not random:

hey must be forced by the template. This implies that if a particular morpheme

rder is favoured by both constraints,

he o

osite order should never be found in

any language (it is harmonically bounded). The following tableau shows this for

applicativized causatives:

[[V

ATI

]

PPLI

ATI

]

> CARP Linear Corres

ondence

[[/v/-/a

licative/]-/causative/] *! *

)

[[/v/-/causative/]-/applicative/]

yman shows that morpheme order variation that would go against both the

late and Linear Corres

ondence is indeed absent.

The second

rediction is a little more involved. If eithe

r Lin

orres

ondence is to be s

lit into constrai

ts mentioning pairs of morphemes, the

following situation can arise. Suppose that there is a template that favours a

heme order /a/-/b/-/c/, and that is s

it int

thr

ee co

traints P

(

recede

)

[/a/-/b/],

P[/a/-/c/] and P[/b/-/c/], plus a general Linear Correspondence principle. This set-up

an have the surprising result that two

orphemes that are

ot ad

acent in the

emplate can occur in one order when separated by a third morpheme, but in the

alternate order when ad

acent

Thi

ows

m th

eco

raint rankin

P[/a/-/b/] >

P[/b/-/c/] > Linear Correspondence > P[/a/-/c/]. Consider an input with A takin

scope over C and B takin

scope over A. As the followin

tableau shows, the

phonological output will be the one that comp

etely complies with th

/b/

/c/

late:

< … C

]

> P

[

/a/-/b/

]

[

/b/-/c/

]

Linear

orrespondence

[

/a/-/c/

]

)

/b/

/c/

/b/

/c/

/b/

/c/

* *

/c/

/b/

/c/

/b/

* * *

Table

ORD

FORMATION IN OPTIMALITY THEORY

onsider next what happens if B is omitted from the input:

< … C

]

> P

[

/a/-/b/

]

[

/b/-/c/

]

Linea

orres

ondence

[

/a/-/c/

]

/c/

)

/c/

omparin

Table 7 with Table 8, we see that the order of /a/ and /c/ has switched

n the two cases. This kind of ‘morpheme metathesis’ does indeed occur in

es with a (partiall

) templatic morpholo

(see Spencer 1991: 210ff).

It is further

redicted that mor

heme metathesis will never affect mor

hemes

hat are adjacent in the overa

l tem

late. This is becaus

for such mor

heme

airs

he mutual ranking between the precedence c

nstraint mentioning them and Linea

orrespondence will determine their ord

in every context, as precedence

onstraints mentioning only one of these

orphemes and another morpheme cannot

nterfere in this case. To the best of our knowledge, there are indeed no languages in

which, sa

, /a/-/b/-/c/ coexi

ts w

ith

/c/

/b/ o

/b/

4.2 Conflicts between Linear C

respondence and other correspondence

const

aints

As we have seen, Linear Correspondence favors a particular orderin

phonolo

ical affixes (or /affix/es). Another, potentiall

conflictin

, mappin

principle states which host an /affix/ can attach to. So far, we have implicitly

assumed that any host with which the /affix/ can form a phonological word will do.

In reality, however, an /affix/ usually

ombines with the phonological correspondent

f the head of the category that the morphosyntactic affix (call it

AFFI

)

combines

with. This condition, formulated in (40), is equivalent to Sadock’s (1991) Strong

Constructional Inte

rit

(

)

Input Correspondenc

AFFIX

selects (a category headed by) X,

AFFIX

is phonologically realized as /affix/, and

A comparable phenomenon can be found in En

lish s

ntax. Bobal

ik (2000) shows

hat there are triples

f adverbs occurring in a fixed order that can be broken when only the highest and lowest adverb

app

ar.

Notice that this anal

sis assum

that the template, rather than Linear Correspondence, is broken up

nto smaller constraints. It is

ossible to achi

e the same result by splitting Linear Correspondence,

but this is somewhat more involved (as it requires

he assumption that the order encountered when all

affixes are present is in fact not the one that is completely in compliance with the template). In

principle, the choice between the two approaches is empirically testable, name

y by considering which

of the orders (the one with all affixes present or

the one with an affix absent) satisfies Linear

orrespondence. We cannot go into this here.

308

PETER A

KEMA

D NEELEMAN

X is phonologically realized as /x/,

affix

tak

es /

f th

FFI

selects a simplex category X, the effect of Input Correspondence is

rivial: /x/ and the /affix/ form a phonological word. In case the

FFI

a m

omplex structure, (40) demands that the corresponding /affix/ forms a phonological

ord with the phonolo

ical realization of the head of that structure, rather than

thin

else. In other words, Input Correspondence favors a mappin

of the left-

branchin

morphos

ntactic structure in (41a) onto the ri

ht-branchin

orphophonological structure in (41b).

(

)

a. [[

Y X

]

AFFIX

]

b. [[/y/ [/x/ /affix/]]

Mappings of the type in (41) provide an alternative to what Hoeksema (1984)

haracterizes as ‘head operations’, morphos

ntactic operations which affect the

properties of a complex cate

(apparentl

) appl

to its head.

The effects of Input Correspondence become particularl

clear when we conside

ases in which it conflicts with Linear Correspondence. An example is provided by

structures in which a com

lex left-headed category is selected by an

AFFIX

that i

spelled out by a /suffix/ (see (42a)). For such structures, Linear Correspondence

ould favor mapping to (42b), whereas Input Correspondence would favor mapping

(

42b’

)

(

)

a. [[

X Y

]

AFFI

]

b. [/x/ [/

/ /affix/]]

b’. [[/x/ /affix/] /y/]

This means that in general morphosyntactic representations like (13a) cannot be

apped onto a morphophonological form without violating at least one mapping

principle. Consider, from this perspec

ive

the case of left-headed Italian

ompounds. Some examples are given below:

These compounds resist further word forma

tion with most, if not all, derivational

suffixes. Althou

can be derived b

aio

and -

ista

(

see

(

)

, the forms

n (45) and (46) are all un

rammatical (Vieri Samek-Lodovici, personal

ommunication

)

(

43) a. carta regalo

paper gif

‘wrapping paper for presents’

b. c

arta

paper carbon

‘carbon

er’

ORD

FORMATION IN OPTIMALITY THEORY

309

(

)

a. cart-iere

‘paper seller’

b. c

art-ai

‘paper worker’

c. c

art-i

‘paper specialist’

(

45) a. *carta regal-iere

a’. *cart-iere regalo

b. *carta regal-aio

b’. *cart-aio regalo

c. ??carta regal-ista

c’. *cart-ista re

alo

(

)

a. ??carta carbon-iere

a’

art-i

arta

n-ai

’

art-ai

c. ?c

arta

n-i

’

art-i

n OT anal

sis of such ‘absolute un

maticalit

’ ma

rel

on the inclusion of

the null parse in the candidate set (see section 2.2), in con

unction with two

onstraints, one requiring the realization of morphemes, the other militating against

artial realization of words. We will not demonstrate this here.

nterestingly, languages can specify that the realization of particular suffixes is

favoured to such an extent that even left-headed compounds derived by them are

allowed to surface. In the case of Italian

s is true of the plural (and perhaps also

the diminutive). A morphosyntactic structure [[

N X

]

RAL

]

is mapped onto a

orphophonolo

ical representation at the cost of violatin

some mappin

principle.

here is a clear

reference to sacrifice

inear Corres

ondence, rather than In

orrespondence, su

estin

a rankin

Parse[PL

RAL

]

>> In

ut Corres

ondence >>

Linear Corres

ondence:

(

47) a. cart-e regalo

paper

PL gif

‘pieces of paper for wrapping presents’

a’. *carta regal-i

paper

t-PL

b. c

art-

bon

‘carbon

ers’

’

arta

n-i

paper carbon