Taylor M.E. Partial Differential Equations III: Nonlinear Equations

Подождите немного. Документ загружается.

338 15. Nonlinear Parabolic Equations

are bounded on R

(and X.0/ D 0). It also applies to BC.R

; R

/.NowifL

is not elliptic, we have no extension of the regularity result in Proposition 1.2.

By a different technique we can show that under certain circumstances, if f be-

longs to a space like H

k;p

; R

/, then a solution u.t/ persists as a solution in



Œ0; T ; H

k;p



as long as it persists as a solution in C



Œ0; T ; C



.To

get this, we reexamine the iterative formula used to solve (4.8), namely

(4.15) u

j C1

.t/ D e

f C

.ts/L



.s/



ds:

As long as (4.9) holds for the Banach space V ,wehave

(4.16)

j C1

.t/k

ke

f k

C C

K.ts/

kX.u

.s//k

 A.t/ C Cte

sup

0st

kX.u

.s//k

and

(4.17) ku

j C1

.t/  u

.t/k

 Cte

sup

0st

kX.u

.s// X.u

j 1

.s//k

Now, as shown in Chap. 13,  3, for such spaces as V D H

k;p

/,thereare

Moser estimates, of the form

(4.18) kuvk

 C kuk

kvk

C C kuk

kvk

and

(4.19) kF.u/k

 C



kuk



1 Ckuk



;C./D sup

jxj;jjk

./

.x/j:

In particular, kX.u/k

satisﬁes an estimate of the form (4.19). Also, we can write

X.u/  X.v/ D Y.u;v/.u  v/; Y.u;v/D



u C .1  /v



d

and obtain the estimate

(4.20)

kX.u/  X.v/k

 C



kuk

Ckvk



ku vk

C C



kuk

Ckvk



kuk

Ckvk



ku vk

From (4.16) we deduce

(4.21) ku

j C1

.t/k

 A.t/ C te

sup

0st



.s/k



1 Cku

.s/k



4. Reaction-diffusion equations 339

If fu

.t/ W j 2 Z

g is bounded in L

.M / for 0  t  T , this takes the form

(4.22) ku

j C1

.t/k

 B

C Bt sup

0st

.s/k

;

for 0  t  T . Also, in such a case, (4.17)and(4.20) yield

(4.23)

j C1

.t/  u

.t/k

 Bt sup

0st

.s/  u

j 1

.s/k

C Bt sup

0st



.s/k

Cku

j 1

.s/k



.s/  u

j 1

.s/k

Now, in (4.22)and(4.23), B may depend on the choice of the space V , but it does

not depend on the V -norm of any u

.s/, only on the L

-norm.

Let us assume that u

.t/ D e

f satisﬁes ku

.t/k

 B

,for0  t 

T; B

 B. This is the B

used in (4.22). Assume T

 1=4B; T

 1=16BB

and T

 T .Thenku

.t/k

 2B

for 0  t  T

,forallj 2 Z

,so

W j 2 Z

g is bounded in C



Œ0; T

; V



. In such a case, (4.23) yields, for

0  t  T

(4.24)

j C1

.t/  u

.t/k



sup

0st

.s/ u

j 1

.s/k

sup

0st

.s/ u

j 1

.s/k

;

so fu

W j 2 Z

g is in fact Cauchy in C



Œ0; T

; V



, having therefore a limit

u 2 C.Œ0;T

; V / satisfying (4.8). The size of the interval Œ0; T

 on which this

argument works depends on the choice of V and the size of ku.0/k

,butnot on

the size of ku.0/k

. We can iterate this argument on intervals of length T

as long

as ku.t/k

is bounded, thus establishing the following.

Proposition 4.2. Suppose V is a Banach space of functions such that (4.9)–(4.10)

and the Moser estimates (4.18)–(4.19) hold. Let f 2 V \ L

.M /, and suppose

(4.8) has a solution u 2 L



Œ0; T /  M



. Then, in fact, u 2 C



Œ0; T /; V



.If

V D H

k;p

.M /, with k  2, we thus have

(4.25) u 2 C



Œ0; T /; H

k;p

.M /



\ C



Œ0; T /; H

k2;p

.M /



;

solving (4.1).

Global existence results can be established for (4.1)whenf takes values in a

bounded subset of R

shown to be invariant under the nonlinear solution operator

to (4.1). An example of this is the following:

Proposition 4.3. In (4.1), assume Lu D Du, where D is a diagonal `  `

matrix with diagonal entries d

 0 and  acts on u componentwise, as the

340 15. Nonlinear Parabolic Equations

Laplace operator on a Riemannian manifold M . Assume M is compact and f 2

k;p

.M; R

/; k > 2 Cn=p. Or assume M D R

, with its Euclidean metric and

f 2 BC

; R

/. Consider a rectangle R  R

,oftheform

(4.26) R Dfy 2 R

W a

 y

 b

Suppose that, for each y 2 @R,

(4.27) X.y/  N<0;

where N is any outer normal to R.Iff takes values in the interior

R of R,then

the solution to (4.1) exists and takes values in

R for all t  0.

Proof. First suppose M is compact. If there is an exit from

R, we can pick .t

such that

(4.28) u

/ D a

or b

;

for some j D 1;:::;`,andu.t; x/ 2

R for all t<t

;x2 M .Pickb

,for

example. Then

(4.29) @

/  0:

Now '.x/ D u

;x/must have a maximum at x D x

,so

(4.30) @

/ D d

u

C X

.u/  X

.u/:

However, (4.27) implies X



u.t



<0,so(4.29)and(4.30) contradict each

other.

In case M D R

, the existence of such .t

/ 2 R

 R

is problematic,

though we can ﬁnd such .t

/ 2 R



,sinceu has a unique continuous

extension to R



and

is compact. We still have @

u.t

/  0,andu

is continuous on R



, but it is not obvious in this case that u.t

/  0,

unless x

lies in R

, not at inﬁnity. Thus we argue as follows.

Let

/ denote ff 2 BC

/ W D

f D 0 at 1; for j˛jD2g.This

Banach space is also one for which Propositions 4.1 and 4.2 work. Furthermore,

the argument above regarding u.t

/ does work if we replace f 2 BC

; R

by f



; R

/. Additionally, we can take a sequence of such f



so that



! f in BC.R

; R

/, and obtain solutions u



such that u



.t; x/ ! u.t; x/

uniformly on Œ0; T  R

for any T<1. We can replace R by a slightly smaller

rectangle R

,forwhich(4.27) holds, and arrange that each f



takes values in

Then u.t; x/ always takes values in R



R. This completes the proof in the case

M D R

4. Reaction-diffusion equations 341

As an example of Proposition 4.3, we consider the Fitzhugh–Nagumo system

(4.2), in which the vector ﬁeld X on R

(4.31) X.v; w/ D



f.v/ w; ".v  w/



;f.v/D v.1  v/.v  a/:

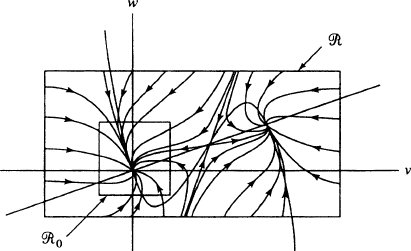
In Fig. 4.1 we illustrate an invariant rectangle R that arises from the choices

(4.32)  D 20; a D 0:4; " D 0:01:

This invariant region contains three critical points of X, two sinks and a saddle.

For this construction to work, we need the following:

The top edge of R lies above the line w D v=;

while the bottom edge of R lies below this line;

the left edge of R lies to the left of the curve w D f.v/;

while the right edge of R lies to the right of this curve.

The two curves mentioned here are the “isoclines,” deﬁning where X

D 0 and

D 0, respectively. The condition just stated implies that X points down on

the top edge of R, up on the bottom edge, to the right on the left edge, and to

the left on the right edge. In Fig. 4.1 we also depict a smaller invariant rectangle

, which contains only one critical point of X, the sink at .0; 0/. Figure 4.2 is

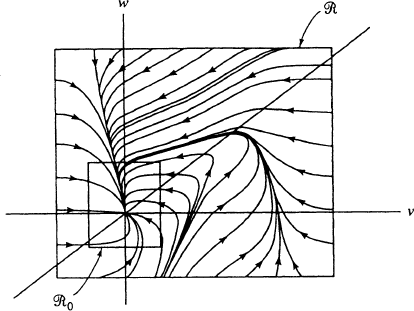
a similar illustration, with  changed from 20 to 10; in this case X has only one

critical point.

The vector ﬁeld (4.31) does not actually satisfy the hypothesis (4.11), since the

coefﬁcients blow up at inﬁnity. But one can alter X outside R to produce a vector

ﬁeld

X to which Propositions 4.1 and 4.2 apply. As long as the initial function

u.0/ D f takes values inside R, one has a solution to (4.2).

While Proposition 4.3 is an elementary consequence of the maximum princi-

ple, this result can also be seen to follow quite transparently from a “nonlinear

FIGURE 4.1 Invariant Rectangles for Fitzhugh-Nagumo System

342 15. Nonlinear Parabolic Equations

FIGURE 4.2 Invariant Rectangles with Different Parameters

Trotter product formula,” namely a solution to (4.1) satisﬁes

(4.33) u.t/ D lim

n!1



.t=n/L

t=n



.f /;

where if F

is the ﬂow on R

generated by X,then

(4.34) F

f.x/ D F



f.x/



We will prove this in the next section. See Proposition 5.4 for a precise

statement. We mention that if f 2 BC

; R

/,then(4.33)convergesin



Œ0; T ; BC

; R



. We can use this result to prove the following, which is

somewhat stronger than Proposition 4.3.

Proposition 4.4. Assume X 2 C

/ and u.0/ D f 2 BC

; R

/, and let

L be a second-order differential operator with constant coefﬁcients, such that e

is a contraction on BC

; R

/,for t  0. Assume there is a family fK

W 0 

s<1g of compact subsets of R

such that each K

has the invariance property

(4.4). Furthermore, assume that

(4.35) F

/  K

sCt

;s;t2 R

If u.0/ D f takes values in K

,then(4.1) has a solution for all t 2 R

, and

u.t; x/ 2 K

Proof. This is a simple consequence of the product formula (4.33).

In cases where L is diagonal and fK

g is a certain shrinking family of rectan-

gles, this result was proved in [RaSm], by different means. An example to which

their result applies arises when K

is the rectangle R

in Fig. 4.1.ThenK

a family of rectangles shrinking to the origin as s !1, and one gets decay

of any solution to (4.2) whose initial function u.0/ D f takes values in such a

4. Reaction-diffusion equations 343

rectangle K

. Of course, if there were no diffusion (i.e., D D 0 in (4.2)), one

would get such decay whenever u.0/ D f took values in the region of R

for

which the origin is an attractor. One then has the question of whether a sufﬁcient

degree of diffusion could change the situation. We will return to this point shortly.

For the system (4.2), there are families of rectangles K

such that K

contains

an arbitrarily large disk centered at the origin, which contract to K

D R, satis-

fying (4.35). Hence any solution to (4.2) with initial data in BC

.R; R

/ exists for

all t  0, and, for t large, u.t/ takes values in R. However, in the cases illustrated

in both Figs. 4.1 and 4.2, there is not a family of rectangles having the property

(4.35)takingR to R

, and in fact not all solutions to (4.2) with initial data in

.R; R

/ will decay to a constant function.

One class of nondecaying solutions to reaction-diffusion equations of particu-

lar interest is the class of “traveling wave solutions,” which, in case M D R and

L has constant coefﬁcients, are sought in the form

(4.36) u.t; x/ D '.x ct/:

Suppose L D D@

,whereD is a diagonal matrix, with entries d

 0.Then'.s/

must satisfy the second-order `  ` system of ODEs:

(4.37) D'

C c'

C X.'/ D 0:

Using D '

, we convert this to a ﬁrst-order .2`/  .2`/ system

(4.38) '

D ;D

Dc  X.'/:

If some d

D 0, it is best not to use

Let us ﬁrst take a closer look at the scalar case, which we write as

(4.39)

D D

C g.v/:

Then a traveling wave v.t; x/ D '.x  ct/ arises when '.s/ satisﬁes the single

ODE

(4.40) D'

C c'

C g.'/ D 0:

With D '

,wehavethe2  2 system

(4.41) '

D ;

Dc  g.'/;

taking D D 1 without essential loss of generality. This is amenable to a simple

phase-plane analysis.

The vector ﬁeld Y D Y

whose orbits are speciﬁed by (4.41) has critical points

at D 0; g.'/ D 0. For a general smooth g in (4.39)–(4.41), if ' D ˛ is a zero

344 15. Nonlinear Parabolic Equations

of g,andifg

.˛/ D , then the linearized ODE about the critical point .˛; 0/

of Y is

(4.42)

D Au;AD



 c



Note that

(4.43) Tr A Dc; det A D :

This establishes the following:

Lemma 4.5. If g.˛/ D 0, the critical point .˛; 0/ of the vector ﬁeld Y deﬁned by

(4.41)is

a saddle if g

.˛/ < 0;

asinkifg

.˛/ > 0 and c>0;

a source if g

.˛/ > 0 and c<0:

Of course, when c D 0,(4.41) is in Hamiltonian form, with energy function

(4.44) E.'; / D

C G.'/; G.'/ D

g.'/ d':

In that case, the integral curves of Y are the level curves of E.'; /, and a non-

degenerate critical point for Y is either a saddle or a center. For c D 0; v.t; x/ D

'.x/ is a stationary solution to the PDE (4.39). If c ¤ 0, we can switch signs of

s if necessary and assume c>0.Then(4.40) models motion on a line, in a force

ﬁeld, with damping, due to friction proportional to the velocity. On any orbit of

(4.41)wehave

(4.45)

Dc .s/

 0:

This implies that Y cannot have a nontrivial periodic orbit if c>0.

Let us consider a case where g has three distinct zeros, ˛

;˛

, as depicted

in Fig. 4.3. In this case, Y has saddles at .˛

;0/and .˛

;0/,andasinkat.˛

;0/.

Now the three points .˛

;0/ are also critical points of the function E.'; /,de-

ﬁned by (4.44), and, depending on whether the critical values at .˛

;0/and .˛

;0/

are equal or not, the level curves of E.'; / (orbits of the c D 0 case of (4.41))

are as depicted in Fig. 4.4.Whenwetakesmallc>0, the orbits of Y in the

cases (a) and (b), respectively, are perturbed to those depicted in Fig. 4.5. In case

(a), both saddles are connected to the sink, while in case (b) just one saddle is

connected to the sink.

In case (b), if we let c increase, eventually the phase plane has the same be-

havior as (a). There will consequently be a particular value c D c

where an orbit

connects the saddle .˛



;0/ to the saddle .˛



;0/,where˛



is the zero of g for

4. Reaction-diffusion equations 345

FIGURE 4.3 Function with Three Zeros

FIGURE 4.4 Vector Fields with Centers

FIGURE 4.5 Vector Fields with Spiral Sinks

which G.'/ D

g.'/ d' has the largest value. An orbit connecting two differ-

ent saddles is called a “heteroclinic orbit.” (Note that in case (b), at c D 0 there

is an orbit connecting the other saddle .˛



;0/ to itself; such an orbit is called a

“homoclinic orbit.”) In an obvious sense, ˛



is the endpoint (either ˛

or ˛

)ofthe

“smaller” of the two “humps” of D g.'/ in Fig. 4.3, the size being measured

by the area enclosed by the curve and the horizontal axis.

Such an orbit of Y connecting .˛



;0/ to .˛



;0/ then gives rise to a traveling

wave solution u.t; x/ D '.x  c

t/, which, for each t  0, tends to ˛



as x !

1 and to ˛



as x !C1.If˛



is the remaining zero of g.v/, then for each

c>0, there is a traveling wave u.t; x/ D e'.x  ct/, which tends to ˛



x !1and to ˛



as x !C1;andifc>c

, there is a traveling wave

u.t; x/ D '.x  ct/, which tends to ˛



as x !1and to ˛



as x !C1.

346 15. Nonlinear Parabolic Equations

Such traveling waves yield a transport of quantities much faster than straight

diffusion processes, described by @u=@t D Du. Yet this speed is due not to any

convective term in (4.1), but rather to the coupling with the nonlinear term X.u/.

Such behavior, according to Murray [Mur], was “a major factor in starting the

whole mathematical ﬁeld of reaction-diffusion theory.”

Note that in the limiting case of (4.2)where" D 0; w D w

is independent of

t, and we get a scalar equation of the form (4.39), with g.v/ D f.v/ w

,ifw

is also independent of x. Another widely studied example of (4.39)is

(4.46) g.v/ D v.1  v/:

In this case the vector ﬁeld Y has two critical points: a saddle and a sink. This case

of (4.39) is called the Kolmogorov–Petrovskii–Piskunovequation. It is also called

the Fisher equation, when studied as a model for the spread of an advanlabeleous

gene in a population; see [Mur].

If (4.1)isa2 2 system with L D D, then one gets a vector ﬁeld on R

from

(4.38), provided D is positive-deﬁnite. If d

>0but d

D 0, then, as noted above,

one omits

and obtains a 3 3 system. For example, for the Fitzhugh–Nagumo

system (4.2), one obtains traveling waves u D .v; w/ D .'

/, provided'

and

satisfy the system

(4.47)

;

D



C f.'

/  '



;

D



 '



This has the form

(4.48) 

D Z

./;

for  D .'

;

/,whereZ

is a vector ﬁeld on R

Various techniques have been brought to bear to analyze orbits of such a vec-

tor ﬁeld. An important role has been played by C. Conley’s theory of “isolating

blocks”; see [Car, Con, Smo]. It has been shown that, for small positive ",there

exist c such that Z

has a periodic orbit, yielding periodic traveling waves for

(4.2). Also, for certain c D c."/, Z

has been shown to have a homoclinic orbit,

with .0;0;0/as limit point. Such homoclinic orbits have been found numerically,

with the aid of computer graphics, in [Rab]. The traveling wave arising from such

a homoclinic orbit is called a pulse. (It follows from (4.45) that such a pulse cannot

arise for scalar equations of the form (4.39)ifD>0:) There is a phenomeno-

logical interpretation when (4.2) is taken as a model of activity along the axon of

a nerve. As seen above, a sufﬁciently small initial condition



.x/; w

.x/



pro-

duces a solution decaying to .0; 0/ at t !1. This traveling wave then arises from

a sufﬁciently large initial condition. One says a “threshold behavior” is involved.

4. Reaction-diffusion equations 347

For a variant of the Fitzhugh–Nagumo system proposed by H. McKean, [Wan]

has established the existence of “multiple impulse” traveling wave solutions.

An interesting question is the following: For given initial data, when can you

say that the solution u.t/ behaves for large t like a traveling wave? For the

Kolmogorov–Petrovskii–Piskunov equation, work has been done on this question

in [KPP]and[McK]. For other work, see [AW1, AW2, Bram, Fi].

If M D R

;n > 1,andL D D, one can seek a solution to (4.1) in the form

of a traveling plane wave, u.t; x/ D '.x ! ct/,where! 2 R

is a unit vector.

Again '.s/ satisﬁes the ODE (4.37). In addition to plane waves, other interest-

ing sorts arise in the multidimensional case, including “spiral waves” and “scroll

waves.” We won’t go into these here; see [Grin] for an introductory account.

Let us return to the evolution of small initial data f . Recall the argument that,

for sup jf.x/jsufﬁciently small, a solution to the Fitzhugh–Nagumo system (4.2)

decays uniformly to 0. For that argument, we used more than the fact that .0; 0/

is a sink for the vector ﬁeld X in that case; we also used a family of contract-

ing rectangles. It turns out that, for a general reaction-diffusion equation (4.1)for

which X has a sink at p 2 R

, specifying that f.x/ be uniformly close to p does

not necessarily lead to a solution u.t/ tending to p as t !1. One can have the

phenomenon of “diffusion-driven instability,” or a “Turing instability,” which we

now describe. For simplicity, let us assume L D D with D D diag.d

;:::;d

where  is the Laplace operator (acting componentwise) on an `-tuple of func-

tions on a compact manifold M .

We ﬁrst give examples of this instability when X is a linear vector ﬁeld,

X.u/ D M u,sothatLu C X.u/ D .L C M/u is a linear operator. If ff

is an orthonormal basis of L

.M / consisting of eigenfunctions of , satisfying

f

D˛

,thenLu C M u satisﬁes

(4.49) .L C M /.yf

/ D



˛

Dy C My



;y2 R

Now, under the hypothesis that 0 2 R

is a sink for X, we have that both of the

`  ` matrices ˛

D and M have all their eigenvalues in the left half-plane. All

there remains to the construction is the realization that if two matrices have this

property but do not commute, then their sum need not have this property. Consider

the following 2 2 case:

(4.50) D D





;MD



b  1a

b a



Assume 0<b<1C a

;a>0. Thus Tr M D b  .1 C a

/<0, while det

M D a

>0,soM has spectrum in the left half-plane. As before, assume d>0.

With  D ˛

, consider

(4.51) N D M  D D



b  1  a

b a

 d

