Szilas A.P. Production and transport of oil and gas, Gathering and Transportation
Подождите немного. Документ загружается.

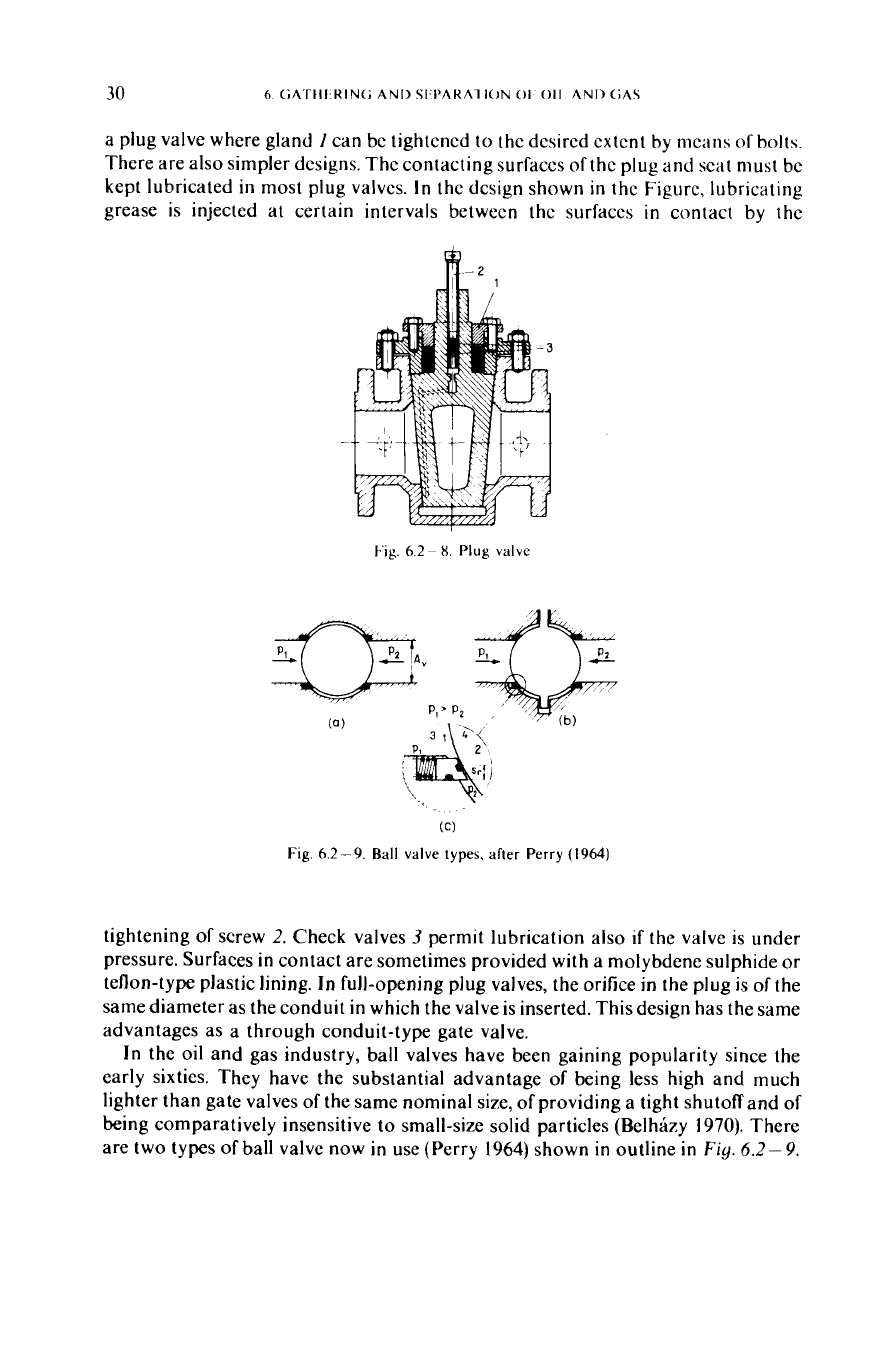
a plug valve where gland
I
can be tightened to the desired extent by means
of
bolts.
There are also simpler designs. The contacting surfaces
of
thc plug and scat must be
kept lubricated
in
most plug valves.
In
the design shown
in
the Figure, lubricating
grease is injected at certain intervals between the surfaces
in
contact by the
Fig.
6.2
~
8.
Plug
valve
(C)
Flg
6 2
-
9
Ball
valve
types,
after
Perry
(1964)
tightening
of
screw
2.
Check valves
3
permit lubrication also
if
the valve is under
pressure. Surfaces in contact are sometimes provided with a molybdene sulphide
or
teflon-type plastic lining.
In
full-opening plug valves, the orifice in the plug
is
of
the
same diameter
as
the conduit in which the valve is inserted. This design has the same
advantages as
a
through conduit-type gate valve.
In the oil and gas industry, ball valves have been gaining popularity since the
early sixties. They have the substantial advantage
of
being less high and much
lighter than gate valves of the same nominal size,
of
providing a tight shutoff and of
being comparatively insensitive to small-size solid particles (Belhhzy 1970). There
are two types
of
ball valve now in
use
(Perry
1964)
shown
in
outline
in
Fig.
6.2
-
9.
6
2 VALVLS.
PRESSURE
RLGIJL.ATORS
31
Solution (a) is provided with a floating ball, which means that the ball may be moved
axially by the pressure differential and may be pressed against the valve seat on the
low-pressure side. This latter seat is usually made of some sort of plastic, e.g. teflon.
The resultant force pressing the ball against the seat is
F=(p,
-p2)A,,,
that is,
it
equals the differential
in
pressure forces acting upon a valve cross-section equal to
the pipe cross-section
A,.
.
If
F
is great, then the pressure on the plastic seal ring is
liable to exceed the permissible maximum.
It
is
in
such cases that solution (b)
will
help.
An
upper and a lower pin integral with the ball will prevent pipe-axial
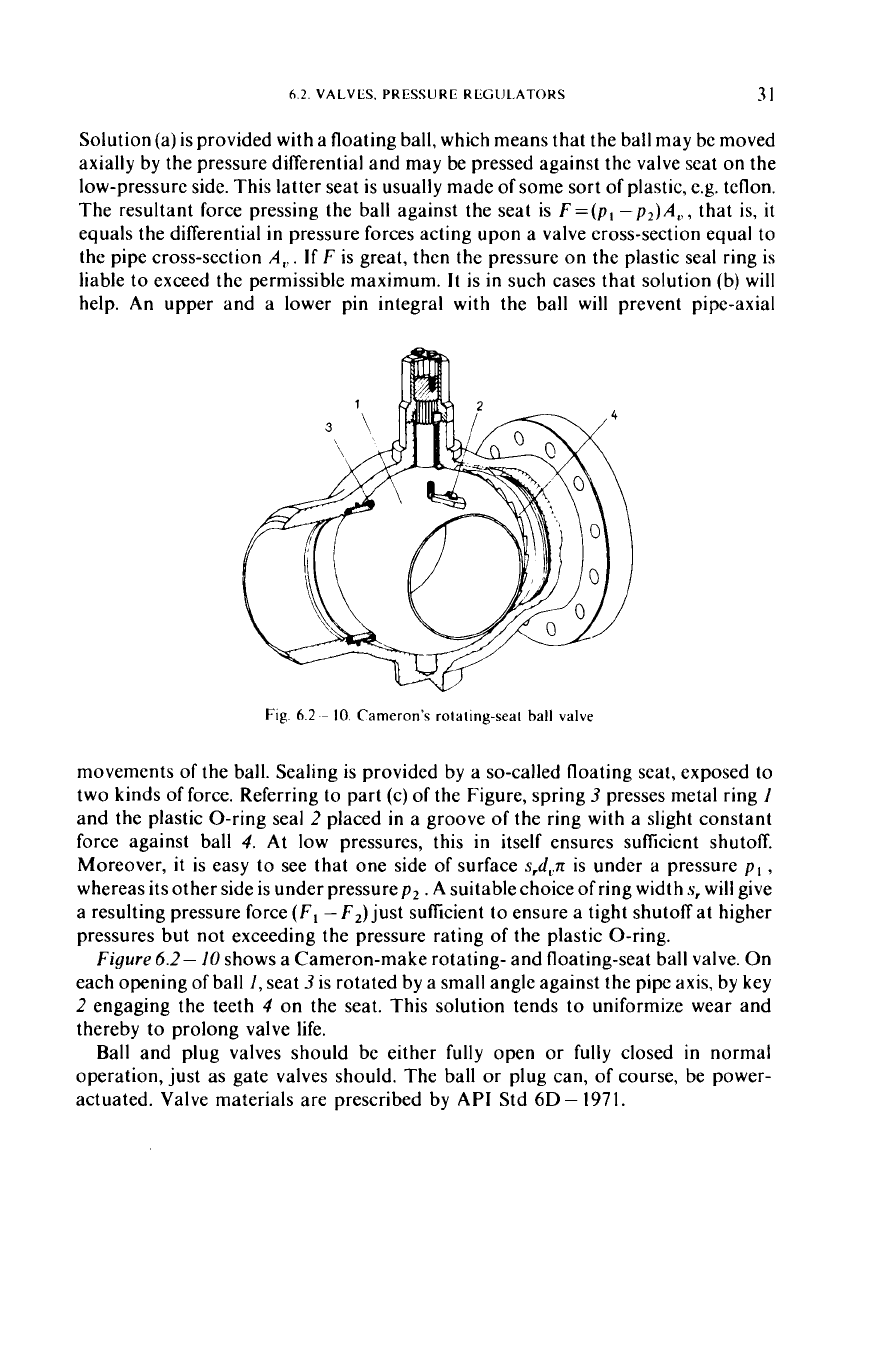
Fig.
6.2
~
10.
Cameron’s
rotalingseal
ball
valve
movements of the ball. Sealing is provided by a so-called floating seat, exposed to
two kinds of force. Referring to part
(c)
of the Figure, spring
3
presses metal ring
1
and the plastic O-ring seal
2
placed in a groove of the ring with a slight constant
force against ball
4.
At
low pressures, this
in
itself ensures sufficient shutoff.
Moreover,
it
is easy to see that one side of surface
S,~,TC
is under a pressure
p,
,
whereas its other side is under pressure
p,
.
A
suitable choice of ring width
s,
will give
a resulting pressure force
(F,
-
F,)
just sufficient to ensure a tight shutoff at higher
pressures but not exceeding the pressure rating of the plastic O-ring.
Figure
6.2-
10
shows a Cameron-make rotating- and floating-seat ball valve. On
each opening of ball
I,
seat
3
is rotated by a small angle against the pipe axis, by key
2
engaging the teeth
4
on the seat. This solution tends to uniformize wear and
thereby to prolong valve life.
Ball and plug valves should be either
fully
open or
fully
closed
in
normal
operation, just as gate valves should. The ball or plug can, of course, be power-
actuated. Valve materials are prescribed by API Std
6D-
1971.
(c)
Globe
valves
The wide range of globe valve types has its main
use
in
regulating liquid and pas
flow rates.
A
common trait of these valves is that the plane of the valve seat is either
parallel
to
the vector of inflow into the valve body.
or
the two include an angle of
90
at most. The element
of
obstruction, the so-called inner valve. is moved
perpendicularly to the valve-seat plane by means of a valve stem.
In
the
fully
open
position, the stem is raised at least as high as to allow a cylindrica! gas passage area
equal to the cross-sectional area of the pipe connected
to
the valve.
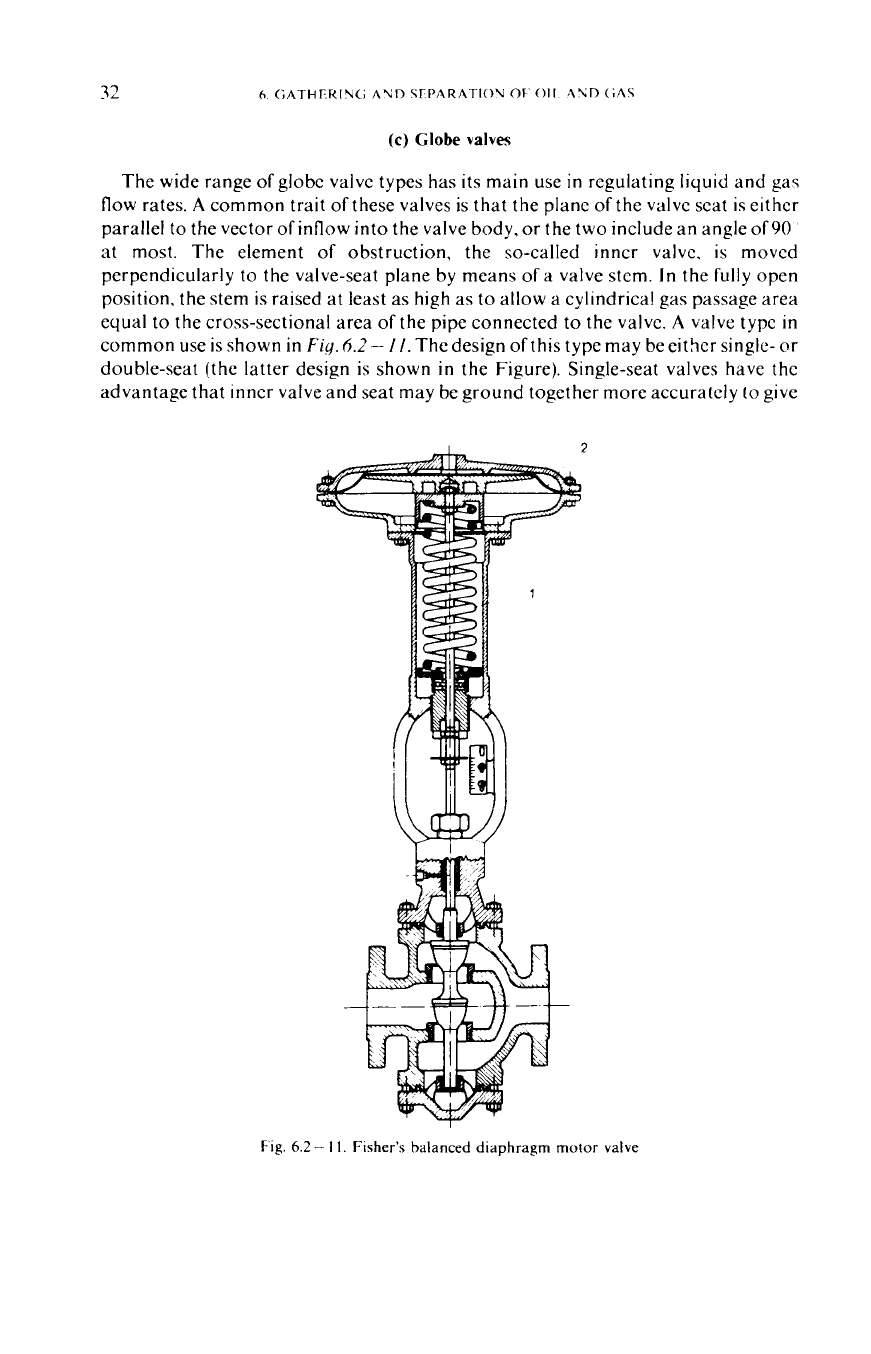
A
valve type
in
common use is shown
in
Fig.
6.2
-
I
I.
The design of this type may be either single- or
double-seat (the latter design is shown in the Figure). Single-seat valves have
the
advantage that inncr valve and seat may
be
ground together more accuratcly to give
2
Fig.
6.2
-
1
1.
Fisher's balanced diaphragm motor valve

6
2.
VALVES.
PRESSURE
REGULATORS
33
a tighter shutoff.
A
high-quality valve should not, when shut off, pass more than
001
percent of its maximum (full-open) throughput. Double-seat valves tend to provide
much lower-grade shutoff. The permissible maximum leakage is
50
times the above
value, that is,
0.5
percent (Sanders 1969). The pressure force acting upon the inner
valve
of
a double-seat valve is almost fully balanced; the forces acting from below
and from above upon the double inner-valve body are almost equal. The force
required to operate the valve is thus comparatively slight. The inner valve
in
a
single-seat design valve is, on the other hand, exposed to a substantial pressure
differential when closed, and the force required to open
it
is therefore quite great.
,
P
(a
1
(b)
(c
1
Fig
6.2
-
12.
Inner-valve designs
According to its design and opening characteristic, the inner valve may be quick-
opening, linear
or
equal-percentage. Part (a) of
Fig.
6.2
-
I2
shows a so-called quick-
opening disc valve.
It
is
used when the aim is
to
either shut off the fluid stream
entirely
or
let
it
pass at
full
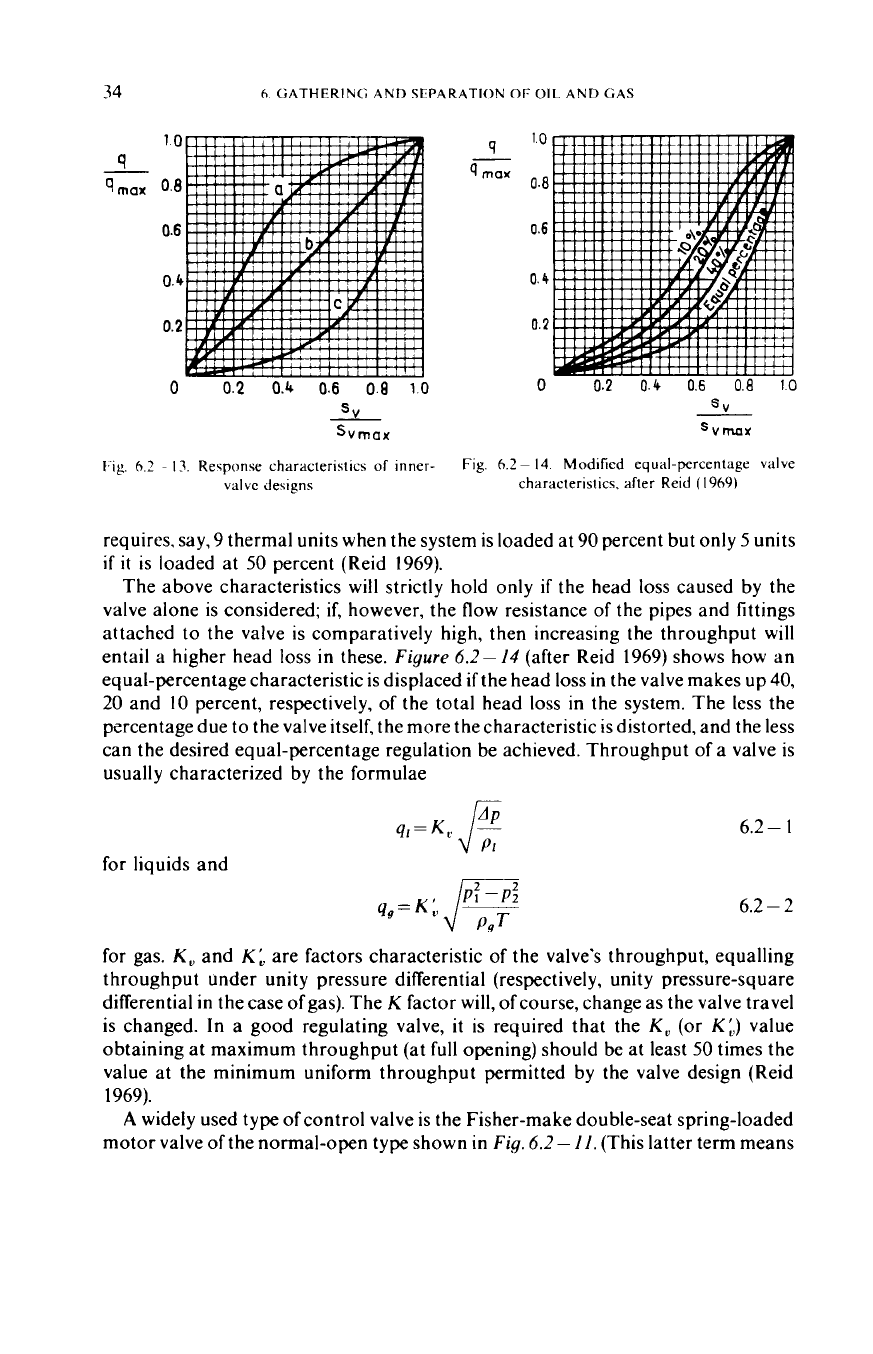
capacity (‘snap action’). The characteristic ofsuch a valve
is graph (a) in
Fig.
6.2-
13.
The graph is a plot of actual throughput related to
maximal throughput
v.
actual valve travel related to total valve travel. Graph (a)
shows that, in a quick-opening valve, throughput attains
0.8
times the
full
value at a
relative valve travel of
0.5.
The inner-valve design shown in part (b) of
Fig.
4.2-
I2
provides the linear characteristic of graph (b) in
Fig.
6.2
-
IS.
In such a valve, a given
throughput invariably entails a given increment in throughput. This type
of
regulation is required e.g. in fluid-level control where, in an upright cylindrical tank,
a given difference in fluid level invariably corresponds to a given difference
in
fluid
content. The inner-valve design shown in part (c) of
Fig.
6.2-
I2
gives rise to a so-
called equal-percentage characteristic (part c, in
Fig.
6.2-
IS).
In a valve of this
design, a given valve travel will invariably change the throughput in a given
proportion. Let e.g.
4/4max
=0.09, in which case the diagram shows
s,/smax
to equal
0.40.
If
this latter is increased by
020
to 0.60, then
4/4,,x
becomes
0.2,
that is, about
2.2
times the preceding value.
A
further increase in relative valve travel by
02
(that is,
to
0.8)
results in a relative throughput of 0.45, which is again round
2.2
times the
foregoing value. This is the type of regulation required e.g. in controlling the
temperature of a system. To bring about a unit change of temperature in the system
34
6
GATHERING
AND
SEPARATION
OF
OIL
AND
GAS
4
max
SV
Svrnax
Fig.
6.2
~
I?.
Response characteristics
of
inner-
valve designs
q
max
-
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
I
o
SV
Svmx
Fig.
6.2
~
14
Modified equal-percentage valve
characteristics. after Reid
(1969)
requires, say, 9 thermal units when the system is loaded at
90
percent but only
5
units
if
it
is
loaded at
50
percent (Reid 1969).
The above characteristics will strictly hold only
if
the head
loss
caused by the
valve alone is considered;
if,
however, the flow resistance of the pipes and fittings
attached to the valve is comparatively high, then increasing the throughput
will
entail a higher head
loss
in
these.
Figure
6.2-
I4
(after Reid 1969) shows how an
equal-percentage characteristic is displaced
if
the head
loss
in
the valve makes up
40,
20 and
10
percent, respectively, of the total head
loss
in the system. The
less
the
percentage due to the valve itself, the more the characteristic is distorted, and the less
can the desired equal-percentage regulation be achieved. Throughput
of
a valve is
usually characterized by the formulae
41=
K,
for liquids and
6.2-
1
6.2
-
2
for
gas.
K,
and
KL,
are factors characteristic of the valve's throughput, equalling
throughput under unity pressure differential (respectively, unity pressure-square
differential in the case
of
gas). The
K
factor will, of course, change as the valve travel
is changed. In a good regulating valve,
it
is required that the
K,
(or
Ki,)
value
obtaining at maximum throughput (at full opening) should be at least
50
times the
value
at
the minimum uniform throughput permitted by the valve design (Reid
1969).
A
widely used type of control valve is the Fisher-make double-seat spring-loaded
motor valve of the normal-open type shown in
Fig.
6.2
-
I
I.
(This latter term means

-.
1
I
2’
13
--
2
I
43
Fig.
6.2
~
17.
Needle valve
that the valve is kept open by spring
1
when no actuating gas pressure acts upon
diaphragm
2.)
The valve is two-way two-position, because
it
has two apertures (one
inlet and one outlet), and the inner valve may occupy two extreme positions (one
open and one closed).
Other diaphragm-type motor valves include the three-way two-position motor
valve shown as
Fig.
6.2-
15.
At
zero actuating-gas pressure, the fluid entering the
valve through inlet
I
emerges through outlet
2.
If
gas pressure is applied, then the
upper inner valve will close and the lower one
will
open, diverting fluid flow to outlet
3.
Figure
6.2- 16
shows a three-way three-position motor valve. The diaphragm
may be displaced by actuating-gas pressure acting from either above or below.
At
36
6.
GATHERING
AND
SEPARATION
OIOIL
AND
GAS
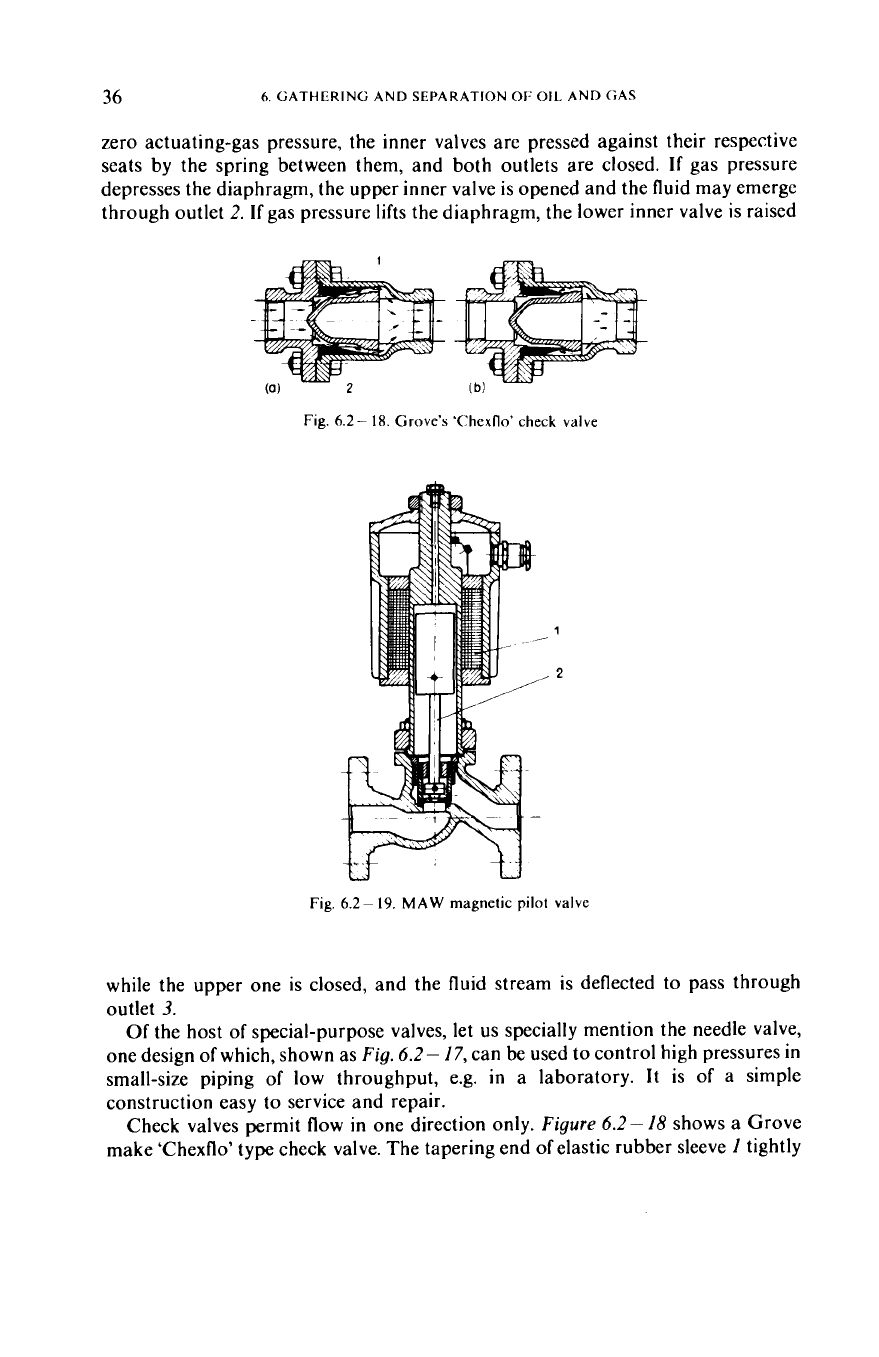
zero actuating-gas pressure, the inner valves are pressed against their respective
seats by the spring between them, and both outlets are closed.
If
gas pressure
depresses the diaphragm, the upper inner valve is opened and the fluid may emerge
through outlet 2.
If
gas pressure lifts the diaphragm, the lower inner valve is raised
Fig.
6.2
-
18.
Grove’s
‘Chexflo’
check
valve
Fig.
6.2-
19.
MAW
magnetic
pilot
1
2
valve
while the upper one is closed, and the fluid stream is deflected
to
pass through
outlet
3.
Of
the host
of
special-purpose valves, let
us
specially mention the needle valve,
one design of which, shown as
Fig.
6.2-
f7,
can be used to control high pressures in
small-size piping
of
low throughput, e.g.
in
a laboratory. It is
of
a simple
construction easy to service and repair.
Check valves permit flow
in
one direction only.
Figure
6.2-
18
shows a Grove
make ‘Chexflo’
type
check valve. The tapering end of elastic rubber sleeve
f
tightly

Design features
Seal
of
closing
element
metallic
elastic
mixed
6
2.
VALVES.
PRESSURE
REGULATORS
e
Table
6.2
-
I.
Advantages
of
various valve designs
(personal communication by
.I.
Bognir)
X X
X
X
X
X
Applicability
-1
J
73
-
-5
- ..
:-
-c
'-1
c7
X
X
X
X
embraces the cylindrical part of central core
2
if
there is no flow
in
the direction
shown in part (a) of the Figure. Even a slight pressure differential from left to right
will, however,
lift
the sleeve from the core and press
it
against the valve barrel. The
valve is thus opened.
A
pressure differential in the opposite sense will prevent flow
by pressing the sleeve even more firmly against the core.
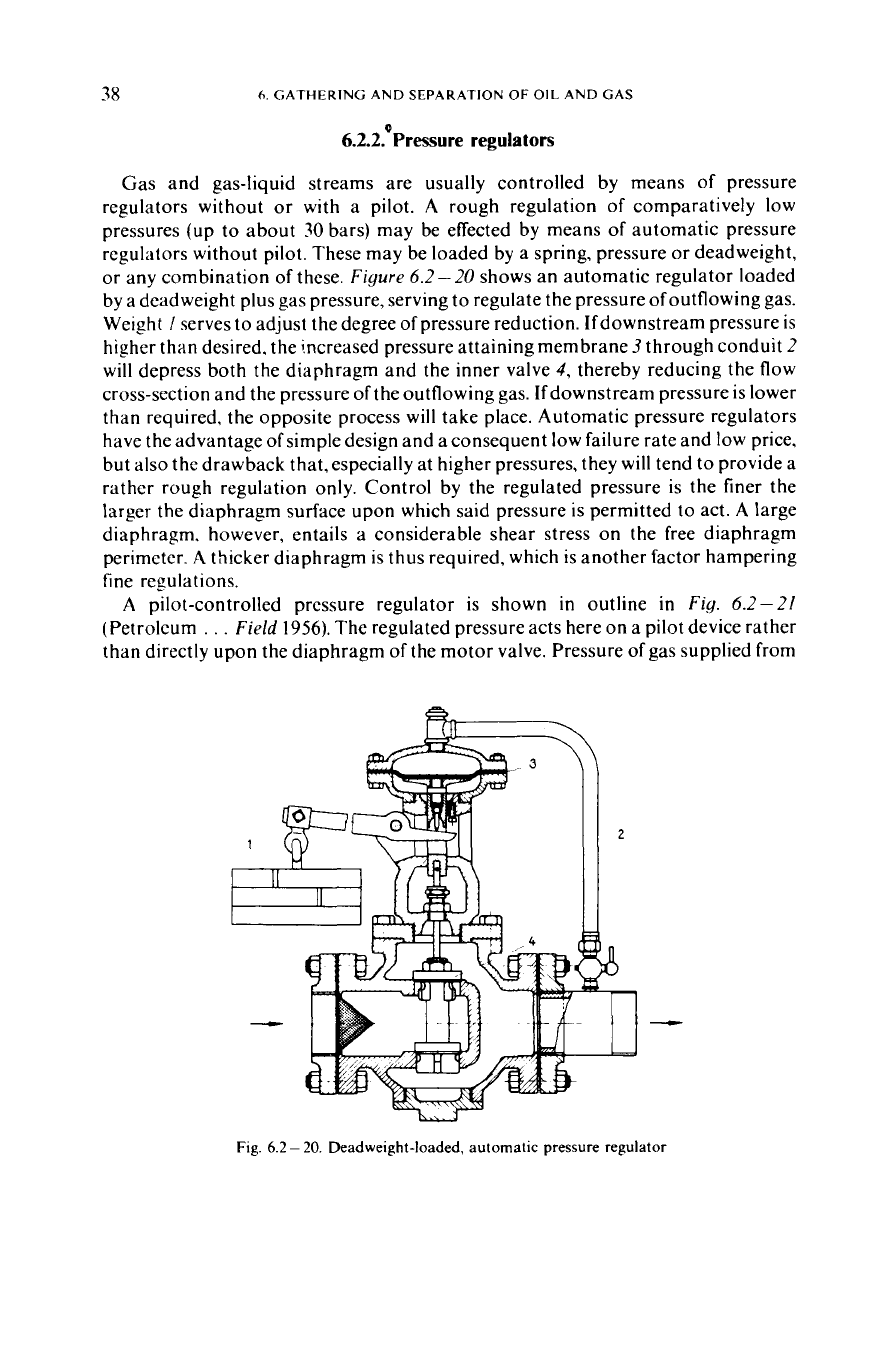
Actuating gas for diaphragm-controlled motor valves is often controlled
in
its
turn by a pilot valve.
Figure
6.2-
19
shows an electromagnetic pilot valve as an
example. Current fed into solenoid
I
will raise soft-iron core
2
and the inner valve
attached to it.
Valve choice is governed by a large number of factors, some of which have been
discussed above.
Table
6.2-
I
is intended to facilitate the choice of the most suitable
design.
38
6.
GATHERING AND SEPARATION
OF
OIL
AND GAS
0
6.2.2.
Pressure regulators
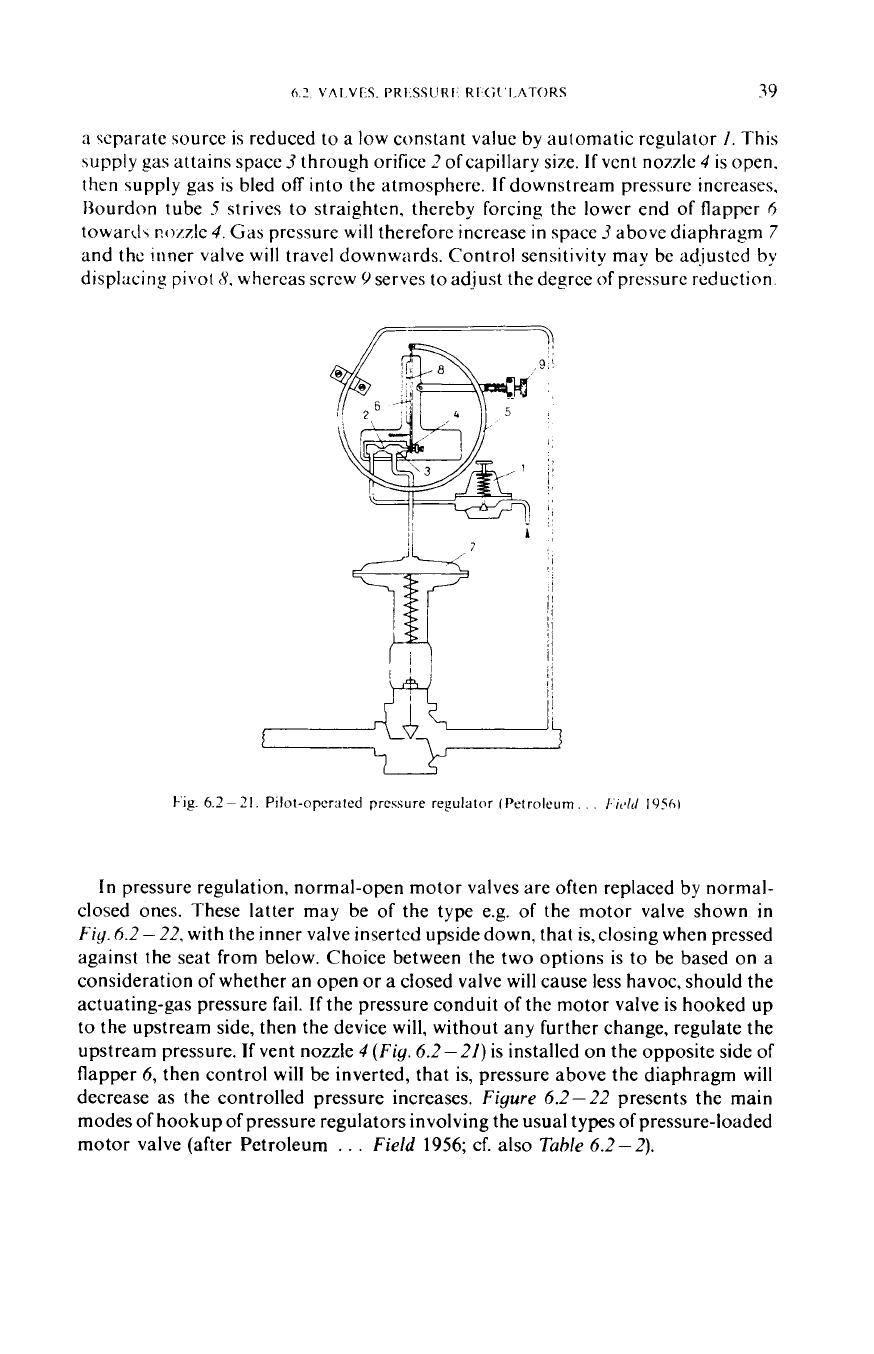
Gas and gas-liquid streams are usually controlled by means of pressure
regulators without or with a pilot.
A
rough regulation of comparatively low
pressures (up to about
30
bars) may be effected by means of automatic pressure
regulators without pilot. These may be loaded by a spring, pressure or deadweight,
or
any combination of these.
Figure
6.2-20
shows an automatic regulator loaded
by a deadweight plus gas pressure, serving to regulate the pressure ofoutflowing gas.
Weight
I
serves to adjust the degree of pressure reduction. Ifdownstream pressure is
higher than desired, the increased pressure attaining membrane
3
through conduit
2
will
depress both the diaphragm and the inner valve
4,
thereby reducing the flow
cross-section and the pressure of the outflowing gas.
If
downstream pressure is lower
than required, the opposite process will take place. Automatic pressure regulators
have the advantage of simple design and
a
consequent low failure rate and low price,
but also the drawback that,especially at higher pressures, they will tend
to
provide a
rather rough regulation only. Control by the regulated pressure is the finer the
larger
the diaphragm surface upon which said pressure is permitted to act.
A
large
diaphragm. however, entails a considerable shear stress on the free diaphragm
perimeter.
A
thicker diaphragm is thus required, which is another factor hampering
fine regulations.
A
pilot-controlled pressure regulator is shown in outline in
Fig.
6.2-21
(Petroleum . .
.
Field
1956).
The regulated pressure acts here on a pilot device rather
than directly upon the diaphragm of the motor valve. Pressure of gas supplied from
Fig.
6.2
-
20.
Deadweight-loaded, automatic pressure regulator
a
separate source is reduced to a low constant value by automatic regulator
1.
This
supply gas attains space
3
through orifice
2
of capillary size.
If
vent nozzle
4
is open.
then supply gas is bled
off
into the atmosphere.
If
downstream pressure increases.
burdon tube
5
strives
to
straighten, thereby forcing the lower end of flapper
6
toward\ ~ozzle
4.
Gas pressure
will
therefore increase
in
space
3
above diaphragm
7
and the inner valve
will
travel downwards. Control sensitivity may be adjusted
by
displacing
pivot
8.
whereas screw
Y
serves to adjust the degree of pressure reduction
I
Fig.
6.2
~
2
2
I.
Pilot-operated presure regulator (Petroleum
pressure regulation. normal-open motor valves are often replaced by Drmal-
closed ones. These latter may be of the type e.g. of the motor valve shown
in
Fig.
6.2
-
22,
with the inner valve inserted upside down, that is, closing when pressed
against the seat from below. Choice between the two options is to be based on a
consideration of whether an open or a closed valve will cause less havoc, should the
actuating-gas pressure fail.
If
the pressure conduit of the motor valve is hooked up
to the upstream side, then the device will, without any further change, regulate the
upstream pressure.
If
vent nozzle
4
(Fig.
6.2- 21)
is installed on the opposite side of
flapper
6,
then control will be inverted, that is, pressure above the diaphragm will
decrease as the controlled pressure increases.
Figure
6.2-22
presents the main
modes of hookup of pressure regulators involving the usual types of pressure-loaded
motor valve (after Petroleum
.
. .
Field
1956; cf. also
Tuble
6.2-2).
