Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students
Подождите немного. Документ загружается.


8.2 Spherical harmonics 275
R
R
0
Figure 8.8 Deformed planet.
Observe that, to first order in η, this deformation does not alter the volume of the body.
Assuming that the planet has a uniform density ρ
0
, compute the external gravitational
potential of the planet.
The gravitational potential obeys Poisson’s equation
∇
2
φ = 4πGρ(x), (8.46)
where G is Newton’s gravitational constant. We expand φ as a power series in η
φ(r, θ) = φ
0
(r, θ) + ηφ
1
(r, θ) + ... (8.47)
We also decompose the gravitating mass into a uniform undeformed sphere, which gives
the external potential
φ
0,ext
(r, θ) =−
4
3
πR
3
0
ρ
0
G
r
, r > R
0
, (8.48)
and a thin spherical shell of areal mass-density
σ(θ) = ρ
0
ηP
2
(cos θ). (8.49)
The thin shell gives rise to the potential
φ
1,int
(r, θ) = Ar
2
P
2
(cos θ), r < R
0
, (8.50)
and
φ
1,ext
(r, θ) = B
1
r
3
P
2
(cos θ), r > R
0
. (8.51)
276 8 Special functions
At the shell we must have φ
1,int
= φ
1,ext
and
∂φ
1,ext
∂r
−
∂φ
1,int
∂r
= 4πGσ(θ). (8.52)
Thus A = BR
−5
0
, and
B =−
4
5
πGηρ
0
R
4
0
. (8.53)
Putting this together, we have
φ(r, θ) =−
4
3
πGρ
0
R
3
0
1
r
−
4
5
πGηρ
0
R
4
0
P
2
(cos θ)
r
3
+ O(η
2
), r > R
0
. (8.54)
8.2.3 General spherical harmonics
When we do not have axisymmetry, we need the full set of spherical harmonics. These
involve solutions of
d
dx
(1 − x
2
)
d
dx
+ l(l + 1) −
m
2
1 − x
2
= 0, (8.55)
which is the associated Legendre equation. This looks like another complicated equation
with singular endpoints, but its bounded solutions can be obtained by differentiating
Legendre polynomials. On substituting y = (1 −x
2
)
m/2
z(x) into (8.55), and comparing
the resulting equation for z(x) with the m-th derivative of Legendre’s equation, we
find that
P
m
l
(x)
def
= (−1)
m
(1 − x
2
)
m/2
d
m
dx
m
P
l
(x) (8.56)
is a solution of (8.55) that remains finite (m = 0) or goes to zero (m > 0) at the endpoints
x =±1. Since P
l
(x) is a polynomial of degree l, we must have P
m
l
(x) = 0ifm > l. For
each l, the allowed values of m in this formula are therefore 0, 1, ..., l. Our definition
(8.56)oftheP
m
l
(x) can be extended to negative integer m by interpreting d
−|m|
/dx
−|m|
as an instruction to integrate the Legendre polynomial m times, instead of differentiating
it, but the resulting P
−|m|
l
(x) are proportional to P
m
l
(x), so nothing new is gained by this
conceit.
The spherical harmonics are the normalized product of these associated Legendre
functions with the corresponding e
imφ
:
Y
m
l
(θ, φ) ∝ P
|m|
l
(cos θ)e
imφ
, −l ≤ m ≤ l. (8.57)
The first few are
l = 0
Y
0
0
=
1
√
4π
(8.58)

8.2 Spherical harmonics 277
l = 1
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
Y
1
1
=−
3
8π
sin θ e
iφ
,
Y
0
1
=
3
4π
cos θ,
Y
−1
1
=
3
8π
sin θ e
−iφ
,
(8.59)
l = 2
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
Y
2
2
=
1
4
15
2π
sin
2
θ e
2iφ
,
Y
1
2
=−
15
8π
sin θ cos θ e
iφ
,
Y
0
2
=
5
4π
3
2
cos
2
θ −
1
2
,
Y
−1
2
=
15
8π
sin θ cos θ e
−iφ
,
Y
−2
2
=
1
4
15
2π
sin
2
θ e
−2iφ
.
(8.60)
The spherical harmonics compose an orthonormal
2π
0
dφ
π
0
sin θdθ
Y
m
l
(θ, φ)
∗
Y
m
l
(θ, φ) = δ
ll
δ
mm
, (8.61)
and complete
∞
l=0
l
m=−l
[Y
m
l
(θ
, φ
)]
∗
Y
m
l
(θ, φ) = δ(φ − φ
)δ(cos θ
− cos θ) (8.62)
set of functions on the unit sphere. In terms of them, the general solution to ∇
2
ϕ = 0is
ϕ(r, θ , φ) =
∞
l=0
l
m=−l
A
lm
r
l
+ B
lm
r
−l−1
Y
m
l
(θ, φ). (8.63)
This is definitely a formula to remember.
For m = 0, the spherical harmonics are independent of the azimuthal angle φ, and so
must be proportional to the Legendre polynomials. The exact relation is
Y
0
l
(θ, φ) =
<
2l + 1
4π
P
l
(cos θ). (8.64)
If we use a unit vector n to denote a point on the unit sphere, we have the symmetry
properties
[Y
m
l
(n)]
∗
= (−1)
m
Y
−m
l
(n), Y
m
l
(−n) = (−1)
l
Y
m
l
(n). (8.65)
These identities are useful when we wish to know how quantum mechanical wavefunc-
tions transform under time reversal or parity.

278 8 Special functions
There is an addition theorem
P
l
(cos γ) =
4π
2l + 1
l
m=−l
[Y
m
l
(θ
, φ
)]
∗
Y
m
l
(θ, φ), (8.66)
where γ is the angle between the directions (θ, φ) and (θ
, φ
), and is found from
cos γ = cos θ cos θ
+ sin θ sin θ
cos(φ − φ
). (8.67)
The addition theorem is established by first showing that the right-hand side is rotation-
ally invariant, and then setting the direction (θ
, φ
) to point along the z-axis. Addition
theorems of this sort are useful because they allow one to replace a simple function of
an entangled variable by a sum of functions of unentangled variables. For example, the
point-charge potential can be disentangled as
1
|r − r
|
=
∞
l=0
l
m=−l
4π
2l + 1
r
l
<
r
l+1
>
[Y
m
l
(θ
, φ
)]
∗
Y
m
l
(θ, φ), (8.68)
where r
<
is the smaller of |r| or |r
|, and r
>
is the greater and (θ, φ), (θ
, φ
) specify the
direction of r, r
, respectively. This expansion is derived by combining the generating
function for the Legendre polynomials with the addition formula. It is useful for defining
and evaluating multipole expansions.
Exercise 8.2: Show that
Y
1
1
Y
0
1
Y
−1
1
⎫
⎬
⎭
∝
⎧
⎨
⎩
x + iy,
z,
x − iy
Y
2
2
Y
1
2
Y
0
2
Y
−1
2
Y
−2
2
⎫
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎭
∝
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
(x + iy)
2
,
(x + iy)z,
x
2
+ y
2
− 2z
2
,
(x − iy)z,
(x − iy)
2
,
where x
2
+y
2
+z
2
= 1 are the usual cartesian coordinates, restricted to the unit sphere.
8.3 Bessel functions
In cylindrical polar coordinates, Laplace’s equation is
0 =∇
2
ϕ =
1
r
∂
∂r
r
∂ϕ
∂r
+
1
r
2
∂
2
ϕ
∂θ
2
+
∂
2
ϕ
∂z
2
. (8.69)
8.3 Bessel functions 279
If we set ϕ = R(r)e
imφ
e
±kx
we find that R(r) obeys
d
2
R
dr
2
+
1
r
dR
dr
+
k
2
−
m
2
r
2
R = 0. (8.70)
Now
d
2
y
dx
2
+
1
x
dy
dx
+
1 −
ν
2
x
2
y = 0 (8.71)
is Bessel’s equation and its solutions are Bessel functions of order ν. The solutions for R
will therefore be Bessel functions of order m, but with x replaced by kr.
8.3.1 Cylindrical Bessel functions
We now set about solving Bessel’s equation,
d
2
y
dx
2
+
1
x
dy
dx
+
1 −
ν
2
x
2
y (x) = 0. (8.72)
This has a regular singular point at the origin, and an irregular singular point at infinity.
We seek a series solution of the form
y = x
λ
(1 + a
1
x + a
2
x
2
+···), (8.73)
and find from the indicial equation that λ =±ν. Setting λ = ν and inserting the series
into the equation, we find, with a conventional choice for normalization, that
y = J
ν
(x)
def
=
x
2
ν
∞
n=0
(−1)
n
n!(n + ν)!
x
2
2n
. (8.74)
Here (n+ν)!≡(n+ν +1). The functions J
ν
(x) are called cylindrical Bessel functions.
If ν is an integer we find that J
−n
(x) = (−1)
n
J
n
(x), so we have only found one of the
two independent solutions. It is therefore traditional to define the Neumann function
N
ν
(x) =
J
ν
(x) cos νπ − J
−ν
(x)
sin νπ
, (8.75)
as this remains an independent second solution even as ν becomes integral. At short
distance, and for ν not an integer
J
ν
(x) =
x
2
ν
1
(ν + 1)
+···,
N
ν
(x) =
1
π
x
2
−ν
(ν) +··· (8.76)
280 8 Special functions
When ν tends to zero, we have
J
0
(x) = 1 −
1
4
x
2
+···
N
0
(x) =
2
π
(ln x/2 + γ)+···, (8.77)
where γ = 0.57721 ...denotes the Euler–Mascheroni constant. For fixed ν, and x ν,
we have the asymptotic expansions
J
ν
(x) ∼
<
2
πx
cos
x −
1
2
νπ −
1
4
π
1 + O
1
x
, (8.78)
N
ν
(x) ∼
<
2
πx
sin
x −
1
2
νπ −
1
4
π
1 + O
1
x
. (8.79)
It is therefore natural to define the Hankel functions
H
(1)
ν
(x) = J
ν
(x) + iN
ν
(x) ∼
<
2
πx
e
i(x−νπ/2−π/4)
, (8.80)
H
(2)
ν
(x) = J
ν
(x) − iN
ν
(x) ∼
<
2
πx
e
−i(x−νπ/2−π/4)
. (8.81)
We will derive these asymptotic forms in Chapter 19.
Generating function
The two-dimensional wave equation
∇
2
−
1
c
2
∂
2
∂t
2
(r, θ , t) = 0 (8.82)
has solutions
= e
iωt
e
inθ
J
n
(kr), (8.83)
where k =|ω|/c. Equivalently, the two-dimensional Helmholtz equation
(∇
2
+ k
2
) = 0, (8.84)
has solutions e
inθ
J
n
(kr). It also has solutions with J
n
(kr) replaced by N
n
(kr), but these
are not finite at the origin. Since the e
inθ
J
n
(kr) are the only solutions that are finite at
the origin, any other finite solution should be expandable in terms of them. In particular,
we should be able to expand a plane-wave solution:
e
iky
= e
ikr sin θ
=
n
a
n
e
inθ
J
n
(kr). (8.85)

8.3 Bessel functions 281
As we will see in a moment, the a
n
’s are all unity, so in fact
e
ikr sin θ
=
∞
n=−∞
e
inθ
J
n
(kr). (8.86)
This generating function is the historical origin of the Bessel functions. They were
introduced by the astronomer Wilhelm Bessel as a method of expressing the eccentric
anomaly of a planetary position as a Fourier sine series in the mean anomaly – a modern
version of Hipparchus’ epicycles.
From the generating function we see that
J
n
(x) =
1
2π
2π
0
e
−inθ+ix sin θ
dθ . (8.87)
Whenever you come across a formula like this, involving the Fourier integral of the
exponential of a trigonometric function, you are probably dealing with a Bessel function.
The generating function can also be written as
e
x
2
t−
1
t
=
∞
n=−∞
t
n
J
n
(x). (8.88)
Expanding the left-hand side and using the binomial theorem, we find
LHS =
∞
m=0
x
2
m
1
m!
%
r+s=m
(r + s)!
r!s!
(−1)
s
t
r
t
−s
&
,
=
∞
r=0
∞
s=0
(−1)
s
x
2
r+s
t
r−s
r!s!
,
=
∞
n=−∞
t
n
∞
s=0
(−1)
s
s!(s + n)!
x
2
2s+n
. (8.89)
We recognize that the sum in the braces is the series expansion defining J
n
(x). This
therefore proves the generating function formula.
Bessel identities
There are many identities and integrals involving Bessel functions. The standard refer-
ence is the monumental Treatise on the Theory of Bessel Functions by G. N. Watson.
Here are just a few formulæ for your delectation:
(i) Starting from the generating function
exp
1
2
x
t −
1
t
=
∞
n=−∞
J
n
(x)t
n
, (8.90)
282 8 Special functions
we can, with a few lines of work, establish the recurrence relations
2J
n
(x) = J
n−1
(x) − J
n+1
(x), (8.91)
2n
x
J
n
(x) = J
n−1
(x) + J
n+1
(x), (8.92)
together with
J
0
(x) =−J
1
(x), (8.93)
J
n
(x + y) =
∞
r=−∞
J
r
(x)J
n−r
(y ). (8.94)
(ii) From the series expansion for J
n
(x) we find
d
dx
x
n
J
n
(x)
= x
n
J
n−1
(x). (8.95)
(iii) By similar methods, we find
1
x
d
dx
m
x
−n
J
n
(x)
= (−1)
m
x
−n−m
J
n+m
(x). (8.96)
(iv) Again from the series expansion, we find
∞
0
J
0
(ax)e
−px
dx =
1
a
2
+ p
2
. (8.97)
Semiclassical picture
The Schrödinger equation
−
2
2m
∇
2
ψ = Eψ (8.98)
can be separated in cylindrical polar coordinates, and has eigenfunctions
ψ
k,l
(r, θ) = J
l
(kr)e
ilθ
. (8.99)
The eigenvalues are E =
2
k
2
/2m. The quantity L = l is the angular momentum of the
Schrödinger particle about the origin. If we impose rigid-wall boundary conditions that
ψ
k,l
(r, θ) vanish on the circle r = R, then the allowed k form a discrete set k
l,n
, where
J
l
(k
l,n
R) = 0. To find the energy eigenvalues we therefore need to know the location
of the zeros of J
l
(x). There is no closed form equation for these numbers, but they are
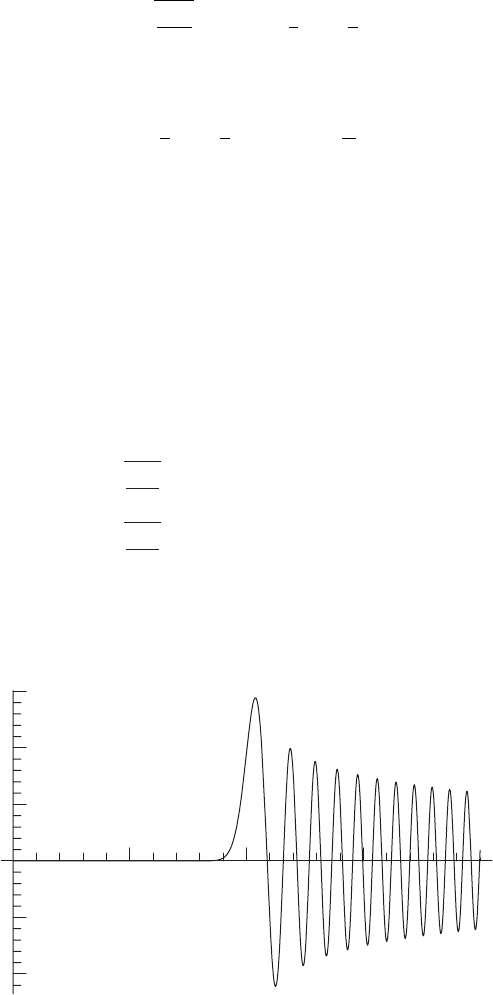
8.3 Bessel functions 283
tabulated. The zeros for kR l are also approximated by the zeros of the asymptotic
expression
J
l
(kR) ∼
<
2
πkR
cos
kR −
1
2
lπ −
1
4
π
, (8.100)
which are located at
k
l,n
R =
1
2
lπ +
1
4
π + (2n + 1)
π
2
. (8.101)
If we let R →∞, then the spectrum becomes continuous and we are describing uncon-
fined scattering states. Since the particles are free, their classical motion is in a straight
line at constant velocity. A classical particle making a closest approach at a distance r
min
has angular momentum L = pr
min
. Since p = k is the particle’s linear momentum,
we have l = kr
min
. Because the classical particle is never closer than r
min
, the quantum
mechanical wavefunction representing such a particle will become evanescent (i.e. tend
rapidly to zero) as soon as r is smaller than r
min
. We therefore expect that J
l
(kr) ≈ 0if
kr < l. This effect is dramatically illustrated by the Mathematica
TM
plot in Figure 8.9.
Improved asymptotic expressions, which give a better estimate of the J
l
(kr) zeros,
are the approximations
J
l
(kr) ≈
<
2
πkx
cos(kx − lθ − π/4), r r
min
,
N
l
(kr) ≈
<
2
πkx
sin(kx − lθ − π/4), r r
min
. (8.102)
Here θ = cos
−1
(r
min
/r) and x = r sin θ are functions of r. They have a geometric origin
in the right-angled triangle in Figure 8.10. The parameter x has the physical interpretation
50 100 150 200
0.1
0.05
0.05
0.1
0.15
Figure 8.9 J
100
(x).
284 8 Special functions
r
min
r
x
kr
min
l
O
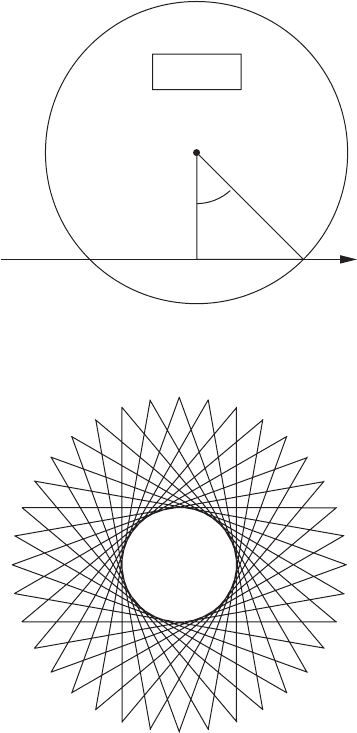
Figure 8.10 The geometric origin of x(r) and θ(r) in (8.102).
Figure 8.11 A collection of trajectories, each missing the origin by r
min
, leaves a “hole”.
of being the distance, measured from the point of closest approach to the origin, along
the straight-line classical trajectory. The approximation is quite accurate once r exceeds
r
min
by more than a few percent.
The asymptotic r
−1/2
fall-off of the Bessel function is also understandable in the
semiclassical picture.
By the uncertainty principle, a particle with definite angular momentum must have
completely uncertain angular position. The wavefunction J
l
(kr)e
ilθ
therefore represents
a coherent superposition of beams of particles approaching from all directions, but all
missing the origin by the same distance (see Figures 8.11 and 8.12). The density of
classical particle trajectories is infinite at r = r
min
, forming a caustic. By “conservation
of lines”, the particle density falls off as 1/r as we move outwards. The particle density
