Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students
Подождите немного. Документ загружается.

7.2 Making waves 245
from Rayleigh’s equation (7.51). Multiplying by ψ
∗
and integrating gives
0 =
y
0
0
dy
ψ
∗
d
2
dy
2
− k
2
ψ + k
∂
2
U
∂y
2
1
(ω − Uk)
|ψ|
2
. (7.58)
An integration by parts then gives
ψ
∗
dψ
dy
y
0
0
=
y
0
0
dy
!
!
!
!
dψ
dy
!
!
!
!
+ k
2
|ψ|
2
+
∂
2
U
∂y
2
1
(U − ω/k)
|ψ|
2
. (7.59)
The lower limit makes no contribution, since ψ
∗
is zero there. On using (7.52) and taking
the imaginary part, we find
Im
ψ
∗
dψ
dy
y
0
= sgn
γ
k
π
∂
2
U
∂y
2
y
c
!
!
!
!
∂U
∂y
!
!
!
!
−1
y
c
|ψ(y
c
)|, (7.60)
or
Im
1
ψ
dψ
dy
y
0
= sgn
γ
k
π
∂
2
U
∂y
2
y
c
!
!
!
!
∂U
∂y
!
!
!
!
−1
y
c
|ψ(y
c
)|
2
|ψ(y
0
)|
2
. (7.61)
This equation is most useful if the interaction with the flow does not substantially perturb
ψ(y) away from the still-water result ψ(y) = sinh(|k|y), and assuming this is so provides
a reasonable first approximation.
If we insert (7.61) into (7.56), where we approximate,
g
k
2
ω
2
≈ g
k
2
ω
2
R
− 2ig
k
2
ω
3
R
γ ,
we find
γ =
ω
3
R
2gk
2
Im
1
ψ
dψ
dy
y
0
= sgn
γ
k
π
ω
3
R
2gk
2
∂
2
U
∂y
2
y
c
!
!
!
!
∂U
∂y
!
!
!
!
−1
y
c
|ψ(y
c
)|
2
|ψ(y
0
)|
2
. (7.62)
We see that either sign of γ is allowed by our analysis. Thus the resonant interaction
between the shear flow and wave appears to lead to either exponential growth or damping
of the wave. This is inevitable because our inviscid fluid contains no mechanism for
dissipation, and its motion is necessarily time-reversal invariant. Nonetheless, as in our
discussion of “friction without friction” in Section 5.2.2, only one sign of γ is actually
observed. This sign is determined by the initial conditions, but a rigorous explanation

246 7 The mathematics of real waves
of how this works mathematically is not easy, and is the subject of many papers. These
show that the correct sign is given by
γ =−π
ω
3
R
2gk
2
∂
2
U
∂y
2
y
c
!
!
!
!
∂U
∂y
!
!
!
!
−1
y
c
|ψ(y
c
)|
2
|ψ(y
0
)|
2
. (7.63)
Since our velocity profile has ∂
2
U /∂y
2
< 0, this means that the waves grow in amplitude.
We can also establish the correct sign for γ by computing the change of momentum
in the background flow due to the wave.
4
The crucial element is whether, in the neigh-
bourhood of the critical depth, more fluid is overtaking the wave than lagging behind it.
This is exactly what the quantity ∂
2
U /∂y
2
measures.
7.3 Nonlinear waves
Nonlinear effects become important when some dimensionless measure of the amplitude
of the disturbance, say P/P for a sound wave, or h/λ for a water wave, is no
longer 1.
7.3.1 Sound in air
The simplest nonlinear wave system is one-dimensional sound propagation in a gas. This
problem was studied by Riemann.
The one-dimensional motion of a fluid is determined by the mass conservation
equation
∂
t
ρ + ∂
x
(ρv) = 0, (7.64)
and Euler’s equation of motion
ρ(∂
t
v +v∂
x
v) =−∂
x
P. (7.65)
In a fluid with equation of state P = P(ρ), the speed of sound, c, is given by
c
2
=
dP
dρ
. (7.66)
It will in general depend on P, the speed of propagation being usually higher when the
pressure is higher.
Riemann was able to simplify these equations by defining a new thermodynamic
variable π(P) as
π =
P
P
0
1
ρc
dP, (7.67)
4
G. E. Vekstein, Amer. J. Phys., 66 (1998) 886.

7.3 Nonlinear waves 247
where P
0
is the equilibrium pressure of the undisturbed air. The quantity π obeys
dπ
dP
=
1
ρc
. (7.68)
In terms of π, Euler’s equation divided by ρ becomes
∂
t
v +v∂
x
v +c∂
x
π = 0, (7.69)
whilst the equation of mass conservation divided by ρ/c becomes
∂
t
π + v∂
x
π + c∂
x
v = 0. (7.70)
Adding and subtracting, we get Riemann’s equations
∂
t
(v +π) + (v + c)∂
x
(v +π) = 0,
∂
t
(v −π) + (v − c)∂
x
(v −π) = 0. (7.71)
These assert that the Riemann invariants v ± π are constant along the characteristic
curves
dx
dt
= v ±c. (7.72)
This tells us that signals travel at the speed v ± c. In other words, they travel, with
respect to the fluid, at the local speed of sound c. Using the Riemann equations, we can
propagate initial data v(x, t = 0), π(x, t = 0) into the future by using the method of
characteristics.
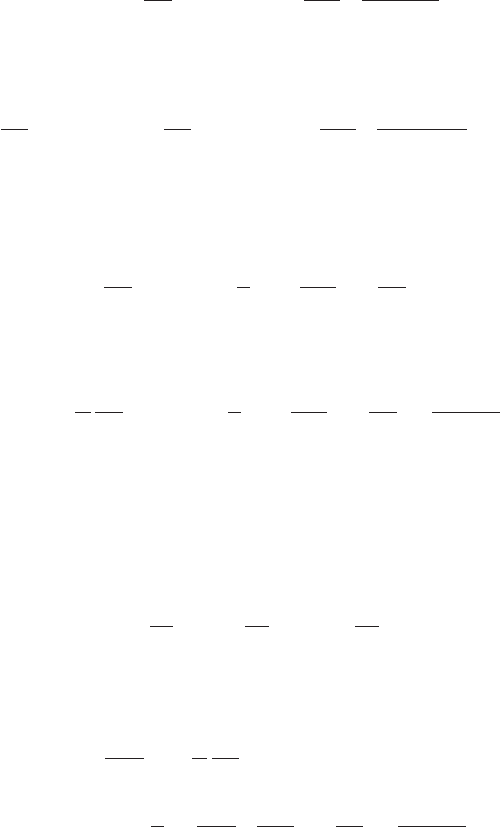
In Figure 7.9 the value of v + π is constant along the characteristic curve C
A
+
, which
is the solution of
dx
dt
= v +c (7.73)
C
A
t
x
AB
P
C
B
Figure 7.9 Nonlinear characteristic curves.

248 7 The mathematics of real waves
passing through A. The value of v − π is constant along C
B
−
, which is the solution of
dx
dt
= v −c (7.74)
passing through B. Thus the values of π and v at the point P can be found if we know
the initial values of v + π at the point A and v − π at the point B. Having found v
and π at P we can invert π(P) to find the pressure P, and hence c, and so continue the
characteristics into the future, as indicated by the dotted lines. We need, of course, to
know v and c at every point along the characteristics C
A
+
and C
B
−
in order to construct
them, and this requires us to treat every point as a “P”. The values of the dynamical
quantities at P therefore depend on the initial data at all points lying between A and B.
This is the domain of dependence of P.
A sound wave caused by a localized excess of pressure will eventually break up
into two distinct pulses, one going forwards and one going backwards. Once these
pulses are sufficiently separated that they no longer interact with one another they are
simple waves. Consider a forward-going pulse propagating into undisturbed air. The
backward characteristics are coming from the undisturbed region where both π and v
are zero. Clearly π − v is zero everywhere on these characteristics, and so π = v.
Now π + v = 2v = 2π is constant on the forward characteristics, and so π and v are
individually constant along them. Since π is constant, so is c. With v also being constant,
this means that c + v is constant. In other words, for a simple wave, the characteristics
are straight lines.
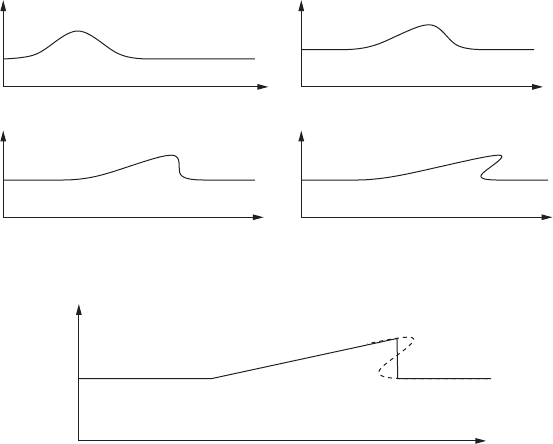
This simple-wave simplification contains within it the seeds of its own destruction.
Suppose we have a positive pressure pulse in a fluid whose speed of sound increases
with the pressure. Figure 7.10 shows how, with this assumption, the straight-line char-
acteristics travel faster in the high-pressure region, and eventually catch up with and
intersect the slower-moving characteristics. When this happens the dynamical variables
will become multivalued. How do we deal with this?
P
x
t
?
Figure 7.10 Simple wave characteristics.
7.3 Nonlinear waves 249
uu
uu
(a) (b)
(d)(c)
?
Figure 7.11 A breaking nonlinear wave.
u
(d)
Figure 7.12 Formation of a shock.
7.3.2 Shocks
Let us untangle the multivaluedness by drawing another set of pictures. Suppose u obeys
the nonlinear “half” wave equation
(∂
t
+ u∂
x
)u = 0. (7.75)
The velocity of propagation of the wave is therefore u itself, so the parts of the wave
with large u will overtake those with smaller u, and the wave will “break”, as shown in
Figure 7.11.
Physics does not permit such multivalued solutions, and what usually happens is that
the assumptions underlying the model which gave rise to the nonlinear equation will no
longer be valid. New terms should be included in the equation which prevent the solution
becoming multivalued, and instead a steep “shock” will form (Figure 7.12).
Examples of an equation with such additional terms are Burgers’ equation
(∂
t
+ u∂
x
)u = ν∂
2
xx
u, (7.76)
and the Korteweg–de Vries (KdV) equation (4.11), which, by a suitable rescaling of x
and t, we can write as
(∂
t
+ u∂
x
)u = δ∂
3
xxx
u. (7.77)
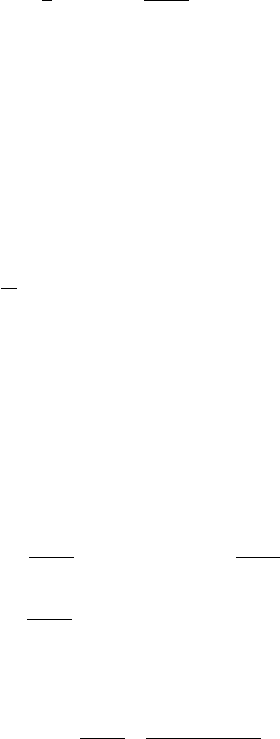
250 7 The mathematics of real waves
Burgers’ equation, for example, can be thought of as including the effects of thermal
conductivity, which was not included in the derivation of Riemann’s equations. In both
these modified equations, the right-hand side is negligible when u is varying slowly, but it
completely changes the character of the solution when the waves steepen and try to break.
Although these extra terms are essential for the stabilization of the shock, once we
know that such a discontinuous solution has formed, we can find many of its properties
– for example the propagation velocity – from general principles, without needing their
detailed form. All we need is to know what conservation laws are applicable.
Multiplying (∂
t
+ u∂
x
)u = 0byu
n−1
, we deduce that
∂
t
1
n
u
n
+ ∂
x
1
n + 1
u
n+1
= 0, (7.78)
and this implies that
Q
n
=
∞
−∞
u
n
dx (7.79)
is time independent. There are infinitely many of these conservation laws, one for each n.
Suppose that the n-th conservation law continues to hold even in the presence of the
shock, and that the discontinuity is at X (t). Then
d
dt
X (t)
−∞
u
n
dx +
∞
X (t)
u
n
dx
= 0. (7.80)
This is equal to
u
n
−
(X )
˙
X − u
n
+
(X )
˙
X +
X (t)
−∞
∂
t
u
n
dx +
∞
X (t)
∂
t
u
n
dx = 0, (7.81)
where u
n
−
(X ) ≡ u
n
(X −) and u
n
+
(X ) ≡ u
n
(X +). Now, using (∂
t
+u∂
x
)u = 0inthe
regions away from the shock, where it is reliable, we can write this as
(u
n
+
− u
n
−
)
˙
X =−
n
n + 1
X (t)
−∞
∂
x
u
n+1
dx −
n
n + 1
∞
X (t)
∂
x
u
n+1
dx
=
n
n + 1
(u
n+1
+
− u
n+1
−
). (7.82)
The velocity at which the shock moves is therefore
˙
X =
n
n + 1
(u
n+1
+
− u
n+1
−
)
(u
n
+
− u
n
−
)
. (7.83)
Since the shock can only move at one velocity, only one of the infinitely many
conservation laws can continue to hold in the modified theory!

7.3 Nonlinear waves 251
Example: Burgers’ equation. From
(∂
t
+ u∂
x
)u = ν∂
2
xx
u, (7.84)
we deduce that
∂
t
u + ∂
x
1
2
u
2
− ν∂
x
u
= 0, (7.85)
so that Q
1
=
udx is conserved, but further investigation shows that no other
conservation law survives. The shock speed is therefore
˙
X =
1
2
(u
2
+
− u
2
−
)
(u
+
− u
−
)
=
1
2
(u
+
+ u
−
). (7.86)
Example: KdV equation. From
(∂
t
+ u∂
x
)u = δ∂
3
xxx
u, (7.87)
we deduce that
∂
t
u + ∂
x
1
2
u
2
− δ∂
2
xx
u
= 0,
∂
t
1
2
u
2
+ ∂
x
1
3
u
3
− δu∂
2
xx
u +
1
2
δ(∂
x
u)
2
= 0
.
.
.
where the dots refer to an infinite sequence of (not exactly obvious) conservation laws.
Since more than one conservation law survives, the KdV equation cannot have shock-like
solutions. Instead, the steepening wave breaks up into a sequence of solitons.
Example: Hydraulic jump, or bore.
A stationary hydraulic jump is a place in a stream where the fluid abruptly increases in
depth from h
1
to h
2
, and simultaneously slows down from supercritical (faster than wave
speed) flow to subcritical (slower than wave speed) flow (Figure 7.13). Such jumps are
v
1
v
2
h
1
h
2
Figure 7.13 A hydraulic jump.
252 7 The mathematics of real waves
commonly seen near weirs, and white-water rapids.
5
A circular hydraulic jump is easily
created in your kitchen sink. The moving equivalent is the tidal bore.
The equations governing uniform (meaning that v is independent of the depth) flow
in channels are mass conservation
∂
t
h + ∂
x
{
hv
}
= 0, (7.88)
and Euler’s equation
∂
t
v +v∂
x
v =−∂
x
{gh}. (7.89)
We could manipulate these into the Riemann form, and work from there, but it is more
direct to combine them to derive the momentum conservation law
∂
t
{hv}+∂
x
hv
2
+
1
2
gh
2
= 0. (7.90)
From Euler’s equation, assuming steady flow, ˙v = 0, we can also deduce Bernoulli’s
equation
1
2
v
2
+ gh = const, (7.91)
which is an energy conservation law. At the jump, mass and momentum must be
conserved:
h
1
v
1
= h
2
v
2
,
h
1
v
2
1
+
1
2
gh
2
1
= h
2
v
2
2
+
1
2
gh
2
2
, (7.92)
and v
2
may be eliminated to find
v
2
1
=
1
2
g
h
2
h
1
(h
1
+ h
2
). (7.93)
A change of frame reveals that v
1
is the speed at which a wall of water of height h =
(h
2
− h
1
) would propagate into stationary water of depth h
1
.
Bernoulli’s equation is inconsistent with the two equations we have used, and so
1
2
v
2
1
+ gh
1
=
1
2
v
2
2
+ gh
2
. (7.94)
This means that energy is being dissipated: for strong jumps, the fluid downstream
is turbulent. For weaker jumps, the energy is radiated away in a train of waves – the
so-called “undular bore”.
5
The breaking crest of Frost’s “white wave” is probably as much an example of a hydraulic jump as of a
smooth downstream wake.

7.3 Nonlinear waves 253
Example: Shock wave in air. At a shock wave in air we have conservation of mass
ρ
1
v
1
= ρ
2
v
2
, (7.95)
and momentum
ρ
1
v
2
1
+ P
1
= ρ
2
v
2
2
+ P
2
. (7.96)
In this case, however, Bernoulli’s equation does hold,
6
so we also have
1
2
v
2
1
+ h
1
=
1
2
v
2
2
+ h
2
. (7.97)
Here, h is the specific enthalpy (U + PV per unit mass). Entropy, though, is not con-
served, so we cannot use PV
γ
= const. across the shock. From mass and momentum
conservation alone we find
v
2
1
=
ρ
2
ρ
1
P
2
− P
1
ρ
2
− ρ
1
. (7.98)
For an ideal gas with c
p
/c
v
= γ , we can use energy conservation to eliminate the
densities, and find
v
1
= c
0
1 +
γ + 1
2γ
P
2
− P
1
P
1
. (7.99)
Here, c
0
is the speed of sound in the undisturbed gas.
7.3.3 Weak solutions
We want to make mathematically precise the sense in which a function u with a
discontinuity can be a solution to the differential equation
∂
t
1
n
u
n
+ ∂
x
1
n + 1
u
n+1
= 0, (7.100)
even though the equation is surely meaningless if the functions to which the derivatives
are being applied are not in fact differentiable.
6
Recall that enthalpy is conserved in a throttling process even in the presence of dissipation. Bernoulli’s
equation for a gas is the generalization of this thermodynamic result to include the kinetic energy of the gas.
The difference between the shock wave in air, where Bernoulli holds, and the hydraulic jump, where it does
not, is that the enthalpy of the gas keeps track of the lost mechanical energy, which has been absorbed by
the internal degrees of freedom. The Bernoulli equation for channel flow keeps track only of the mechanical
energy of the mean flow.

254 7 The mathematics of real waves
We could play around with distributions like the Heaviside step function or the Dirac
delta, but this is unsafe for nonlinear equations, because the product of two distributions
is generally not meaningful. What we do is introduce a new concept. We say that u is a
weak solution to (7.100)if
R
2
dx dt
u
n
∂
t
ϕ +
n
n + 1
u
n+1
∂
x
ϕ
= 0, (7.101)
for all test functions ϕ in some suitable space T . This equation has formally been
obtained from (7.100) by multiplying it by ϕ(x, t), integrating over all space-time, and
then integrating by parts to move the derivatives off u, and onto the smooth function ϕ.
If u is assumed smooth then all these manipulations are legitimate and the new equation
(7.101) contains no new information. A conventional solution to (7.100) is therefore also
a weak solution. The new formulation (7.101), however, admits solutions in which u has
shocks.
Let us see what is required of a weak solution if we assume that u is everywhere
smooth except for a single jump from u
−
(t) to u
+
(t) at the point X (t). Let D
±
be the
regions to the left and right of the jump, as shown in Figure 7.14. Then the weak-solution
condition (7.101) becomes
0 =
D
−
dx dt
u
n
∂
t
ϕ +
n
n + 1
u
n+1
∂
x
ϕ
+
D
+
dx dt
u
n
∂
t
ϕ +
n
n + 1
u
n+1
∂
x
ϕ
.
(7.102)
Let
n =
1
1 +|
˙
X |
2
,
−
˙
X
1 +|
˙
X |
2
(7.103)
x
t
X(t)
D
D
n
Figure 7.14 The geometry of the domains to the right and left of a jump.
