Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

8.3 Bessel functions 295

The first few are

(x) =

sin x,

(x) =

sin x −

cos x,

(x) =



−



sin x −

cos x,

(x) =−

cos x,

(x) =−

cos x −

sin x,

(x) =−



−



cos x −

sin x.

Despite the appearance of negative powers of x, the j

(x) are all finite at x = 0. The

(x) all diverge to −∞ as x → 0. In general

(x) = f

(x) sin x + g

(x) cos(x), (8.163)

(x) =−f

(x) cos(x) + g

(x) sin x, (8.164)

where f

(x) and g

(x) are polynomials in 1/x.

We also define the spherical Hankel functions by

(1)

(x) = j

(x) + in

(x), (8.165)

(2)

(x) = j

(x) − in

(x). (8.166)

These behave like

(1)

(x) ∼

i(x−[l+1]π/2)

, (8.167)

(2)

(x) ∼

−i(x−[l+1]π/2)

, (8.168)

at large x.

The solution to the wave equation regular at the origin is therefore a sum of terms

such as

k,l,m

(r, θ , φ, t) = j

(kr)Y

(θ, φ)e

−iωt

, (8.169)

296 8 Special functions

Figure 8.14 Fission core.

where ω =±ck, with k > 0. For example, the plane wave e

ikz

has expansion

ikz

= e

ikr cos θ

∞



l=0

(2l + 1)i

(kr)P

(cos θ), (8.170)

or equivalently, using (8.66),

ik·r

= 4π

∞



l=0



m=−l

(kr)

(

∗

(ˆr) (8.171)

where

k, ˆr are unit vectors in the direction of k and r, respectively, and are used as a

shorthand notation to indicate the angles that should be inserted into the spherical har-

monics. This angular-momentum-adapted expansion of a plane wave provides a useful

tool in scattering theory.

Exercise 8.4: Peierls’problem. Critical mass. The core of a nuclear device consists of a

sphere of fissile

235

U of radius R. It is surrounded by a thick shell of non-fissile material

which acts as a neutron reflector, or tamper (Figure 8.14).

In the core, the fast neutron density n(r, t) obeys

∂n

∂t

= ν n + D

∇

n. (8.172)

Here the term with ν accounts for the production of additional neutrons due to induced

fission. The term with D

describes the diffusion of the fast neutrons. In the tamper the

neutron flux obeys

∂n

∂t

= D

∇

n. (8.173)

Both the neutron density n and flux j ≡ D

F,T

∇n, are continuous across the interface

between the two materials. Find an equation determining the critical radius R

above

which the neutron density grows exponentially. Show that the critical radius for an

assembly with a tamper consisting of

238

U(D

= D

) is one-half of that for a core

surrounded only by air (D

=∞), and so the use of a thick

238

U tamper reduces the

critical mass by a factor of eight.

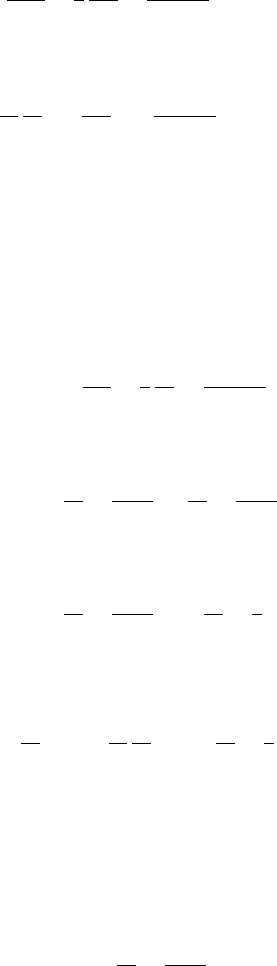
8.3 Bessel functions 297

Factorization and recurrence

The equation obeyed by the spherical Bessel function is

−

dχ

l(l + 1)

= k

, (8.174)

or, in Sturm–Liouville form,

−



dχ



l(l + 1)

= k

. (8.175)

The corresponding differential operator is formally self-adjoint with respect to the inner

product

f , g=



∞

∗

g)x

dx. (8.176)

Now, the operator

=−

−

l(l + 1)

(8.177)

factorizes as



−

l − 1



l + 1



, (8.178)

or as



l + 2



−



. (8.179)

Since, with respect to the w = x

inner product, we have





†

=−

−

, (8.180)

we can write

= A

†

= A

l+1

†

l+1

, (8.181)

where



l + 1



. (8.182)

298 8 Special functions

From this we can deduce

∝ j

l−1

, (8.183)

†

l+1

∝ j

l+1

. (8.184)

The constants of proportionality are in each case unity. The same recurrence formulæ

hold for the spherical Neumann functions n

8.4 Singular endpoints

In this section we will exploit our knowledge of the Laplace eigenfunctions in spherical

and plane polar coordinates to illustrate Weyl’s theory of self-adjoint boundary condi-

tions at singular endpoints. We also connect Weyl’s theory with concepts from scattering

theory.

8.4.1 Weyl’s theorem

Consider the Sturm–Liouville eigenvalue problem

Ly ≡−

[p(r)y



]



+ q(r)y = λy (8.185)

on the interval [0, R]. Here p(r), q(r) and w(r) are all supposed real, so the equation is

formally self-adjoint with respect to the inner product

u, v



∗

v dr. (8.186)

If r = 0 is a singular point of (8.185), then we will be unable to impose boundary

conditions of our accustomed form

ay (0) + by



(0) = 0 (8.187)

because one or both of the linearly independent solutions y

(r) and y

(r) will diverge as

r → 0. The range of possibilities was ennumerated by Weyl:

Theorem: (Hermann Weyl, 1910): Suppose that r = 0 is a singular point and r = Ra

regular point of the differential equation (8.185). Then

I. Either:

(a) Limit-circle case: There exists a λ

such that both of the linearly independent

solutions to (8.185) have a w norm that is convergent in the vicinity of r = 0.In

this case both solutions have convergent w norm for all values of λ.

(b) Limit-point case: No more than one solution has convergent w norm for any λ.

8.4 Singular endpoints 299

II. In either case, whenever Im λ = 0, there is at least one finite-norm solution. When

λ lies on the real axis there may or may not exist a finite norm solution.

We will not attempt to prove Weyl’s theorem. The proof is not difficult and may be

found in many standard texts.

It is just a little more technical than the level of this book.

We will instead illustrate it with enough examples to make the result plausible, and its

practical consequences clear.

When we come to construct the resolvent R

(r, r



) obeying

(L − λI )R

(r, r



) = δ(r − r



) (8.188)

by writing it as a product of y

and y

we are obliged to choose a normalizable function

for y

, the solution obeying the boundary condition at r = 0. We must do this so that

the range of R

will be in L

[0, R]. In the limit-point case, and when Im λ = 0, there

is only one choice for y

. There is therefore a unique resolvent, a unique self-adjoint

operator L−λI of which R

is the inverse, and hence L is a uniquely specified differential

operator.

In the limit-circle case there is more than one choice for y

and hence more than

one way of making L into a self-adjoint operator. To what boundary conditions do these

choices correspond?

Suppose that the two normalizable solutions for λ = λ

are y

(r) and y

(r). The

essence of Weyl’s theorem is that once we are sufficiently close to r = 0 the exact value

of λ is unimportant and all solutions behave as a linear combination of these two. We

can therefore impose as a boundary condition that the allowed solutions be proportional

to a specified real linear combination

y (r) ∝ ay

(r) + by

(r), r → 0. (8.189)

This is a natural generalization of the regular case where we have a solution y

(r) with

boundary conditions y

(0) = 1, y



(0) = 0, so y

(r) ∼ 1, and a solution y

(r) with

(0) = 0, y



(0) = 1, so y

(r) ∼ r. The regular self-adjoint boundary condition

ay (0) + by



(0) = 0 (8.190)

with real a, b then forces y(r) to be

y (r) ∝ by

(r) − ay

(r) ∼ b 1 − ar, r → 0. (8.191)

Example: Consider the radial part of the Laplace eigenvalue problem in two dimensions.

Lψ ≡−



dψ



ψ = k

ψ. (8.192)

For example: Ivar Stackgold Boundary Value Problems of Mathematical Physics, Volume I (SIAM 2000).

When λ is on the real axis then there may be no normalizable solution, and R

cannot exist. This will occur

only when λ is in the continuous spectrum of the operator L, and is not a problem as the same operator L is

obtained for any λ.

300 8 Special functions

The differential operator L is formally self-adjoint with respect to the inner product

ψ, χ=



∗

χ rdr. (8.193)

When k

= 0, the m

= 0 equation has solutions ψ = r

±m

, and, of the normalization

integrals



rdr,



−m

rdr, (8.194)

only the first, containing the positive power of r, is convergent. For m = 0weare

therefore in Weyl’s limit-point case. For m

= 0, however, the k

= 0 solutions are

(r) = 1 and ψ

(r) = ln r. Both normalization integrals



rdr,



|ln r|

rdr (8.195)

converge and we are in the limit-circle case at r = 0. When k

> 0 these solutions

become

(kr) = 1 −

(kr)

+···

(kr) =





[ln(kr/2) + γ ]+··· (8.196)

Both remain normalizable, in conformity with Weyl’s theorem. The self-adjoint bound-

ary conditions at r → 0 are therefore that near r = 0 the allowed functions become

proportional to

1 + α ln r (8.197)

with α some specified real constant.

Example: Consider the radial equation that arises when we separate the Laplace

eigenvalue problem in spherical polar coordinates.

−



dψ



l(l + 1)

ψ = k

ψ. (8.198)

When k = 0 this has solutions ψ = r

, r

−l−1

. For non-zero l only the first of the

normalization integrals



dr,



−2l−2

dr, (8.199)

8.4 Singular endpoints 301

is finite. Thus, for l = 0, we are again in the limit-point case, and the boundary condition

at the origin is uniquely determined by the requirement that the solution be normalizable.

When l = 0, however, the two k

= 0 solutions are ψ

(r) = 1 and ψ

(r) = 1/r.

Both integrals



dr,



−2

dr (8.200)

converge, so we are again in the limit-circle case. For positive k

, these solutions

evolve into

1,k

(r) = j

(kr) =

sin kr

, ψ

2,k

(r) =−kn

(kr) =

cos kr

. (8.201)

Near r = 0, we have ψ

1,k

∼ 1 and ψ

2,k

∼ 1/r, exactly the same behaviour as the k

= 0

solutions.

We obtain a self-adjoint operator if we choose a constant a

and demand that all

functions in the domain be proportional to

ψ(r) ∼ 1 −

(8.202)

as we approach r = 0. If we write the solution with this boundary condition as

(r) =

sin(kr +η)

= cos η



sin(kr)

+ tan η

cos(kr)



∼ k cos η



1 +

tan η



, (8.203)

we can read off the phase shift η as

tan η(k) =−ka

. (8.204)

These boundary conditions arise in quantum mechanics when we study the scattering of

particles whose de Broglie wavelength is much larger than the range of the scattering

potential. The incident wave is unable to resolve any of the internal structure of the

potential and perceives its effect only as a singular boundary condition at the origin. In

this context the constant a

is called the scattering length. This physical model explains

why only the l = 0 partial waves have a choice of boundary condition: classical particles

with angular momentum l = 0 would miss the origin by a distance r

min

= l/k and never

see the potential.

The quantum picture also helps explain the physical origin of the distinction between

the limit-point and limit-circle cases. A point potential can have a bound state that

extends far beyond the short range of the potential. If the corresponding eigenfunction

is normalizable, the bound particle has a significant amplitude to be found at non-

zero r, and this amplitude must be included in the completeness relation and in the

302 8 Special functions

eigenfunction expansion of the Green function. When the state is not normalizable,

however, the particle spends all its time very close to the potential, and its eigenfunction

makes zero contribution to the Green function and completeness sum at any non-zero

r. Any admixture of this non-normalizable state allowed by the boundary conditions

can therefore be ignored, and, as far as the external world is concerned, all boundary

conditions look alike. The next few exercises will illustrate this.

Exercise 8.5: The two-dimensional “delta function” potential. Consider the quantum

mechanical problem in R



−∇

+ V (|r|)

ψ = Eψ

with V an attractive circular square well:

V (r) =



−λ/πa

, r < a

0, r > a.

The factor of πa

has been inserted to make this a regulated version of V (r) =−λδ

(r).

Let µ =



λ/πa

(i) By matching the functions

ψ(r) ∝



(

µr

)

, r < a

(κr), r > a,

at r = a, show that as a becomes small, we can scale λ towards zero in such a way

that the well becomes infinitely deep yet there remains a single bound state with

finite binding energy

≡ κ

−2γ

−4π/λ

It is only after scaling λ in this way that we have a well-defined quantum mechanical

problem with a “point” potential.

(ii) Show that in the scaling limit, the associated wavefunction obeys the singular-

endpoint boundary condition

ψ(r) → 1 + α ln r, r → 0

where

α =

γ + ln κ/2

Observe that by varying κ

between 0 and ∞ we can make α be any real number.

So the entire range of possible self-adjoint boundary conditions may be obtained

by specifying the binding energy of an attractive potential.

8.4 Singular endpoints 303

(iii) Assume that we have fixed the boundary conditions by specifying κ, and consider

the scattering of unbound particles off the short-range potential. It is natural to

define the phase shift η(k) so that

(r) = cos ηJ

(kr) − sin ηN

(kr)

∼

πkr

cos(kr − π/4 +η), r →∞.

Show that

cot η =





ln k/κ.

Exercise 8.6: The three-dimensional “delta function” potential. Repeat the calculation

of the previous exercise for the case of a three-dimensional delta function potential

V (r) =



−λ/(4πa

/3), r < a

0, r > a.

(i) Show that as we take a → 0, the delta function strength λ can be adjusted so that

the scattering length becomes



4πa

−



−1

and remains finite.

(ii) Show that when this a

is positive, the attractive potential supports a single bound

state with external wavefunction

ψ(r) ∝

−κr

where κ = a

−1

Exercise 8.7: The pseudo-potential. Consider a particle of mass µ confined in a large

sphere of radius R. At the centre of the sphere is a singular potential whose effects can

be parametrized by its scattering length a

and the resultant phase shift

η(k) ≈ tan η(k) =−a

In the absence of the potential, the normalized l = 0 wavefunctions would be

(r) =

2πR

sin k

where k

= nπ/R.

304 8 Special functions

(i) Show that the presence of the singular potential perturbs the ψ

eigenstate so that

its energy E

changes by an amount

E



2µ

(ii) Show this energy shift can be written as if it were the result of applying first-order

perturbation theory

E

≈n|V

|n≡



r|ψ

(r)

to an artificial pseudo-potential

(r) =

2πa



(r).

Although the energy shift is small when R is large, it is not a first-order perturbation

effect and the pseudo-potential is a convenient fiction which serves to parametrize the

effect of the true potential. Even the sign of the pseudo-potential may differ from that

of the actual short-distance potential. For our attractive “delta function”, for example,

the pseudo-potential changes from being attractive to being repulsive as the bound state

is peeled off the bottom of the unbound continuum. The change of sign occurs not by

passing through zero, but by it passing through infinity. It is difficult to manipulate a

single potential so as to see this dramatic effect, but when the particles have spin, and a

spin-dependent interaction potential, it is possible to use a magnetic field to arrange for

a bound state of one spin configuration to pass through the zero of energy of the other.

The resulting Feshbach resonance has the same effect on the scattering length as the

conceptually simpler shape resonance obtained by tuning the single potential.

The pseudo-potential formula is commonly used to describe the pairwise interaction of

a dilute gas of particles of mass m, where it reads

(r) =

4πa



(r). (8.205)

The internal energy-density of the gas due to the two-body interaction then becomes

u(ρ) =

4πa



where ρ is the particle-number density.

The factor-of-two difference between the formula in the exercise and (8.205) arises

because the µ in the exercise must be understood as the reduced mass µ = m

/(m+m) =

m/2 of the pair of interacting particles.