Stewart J. College Algebra: Concepts and Contexts
Подождите немного. Документ загружается.

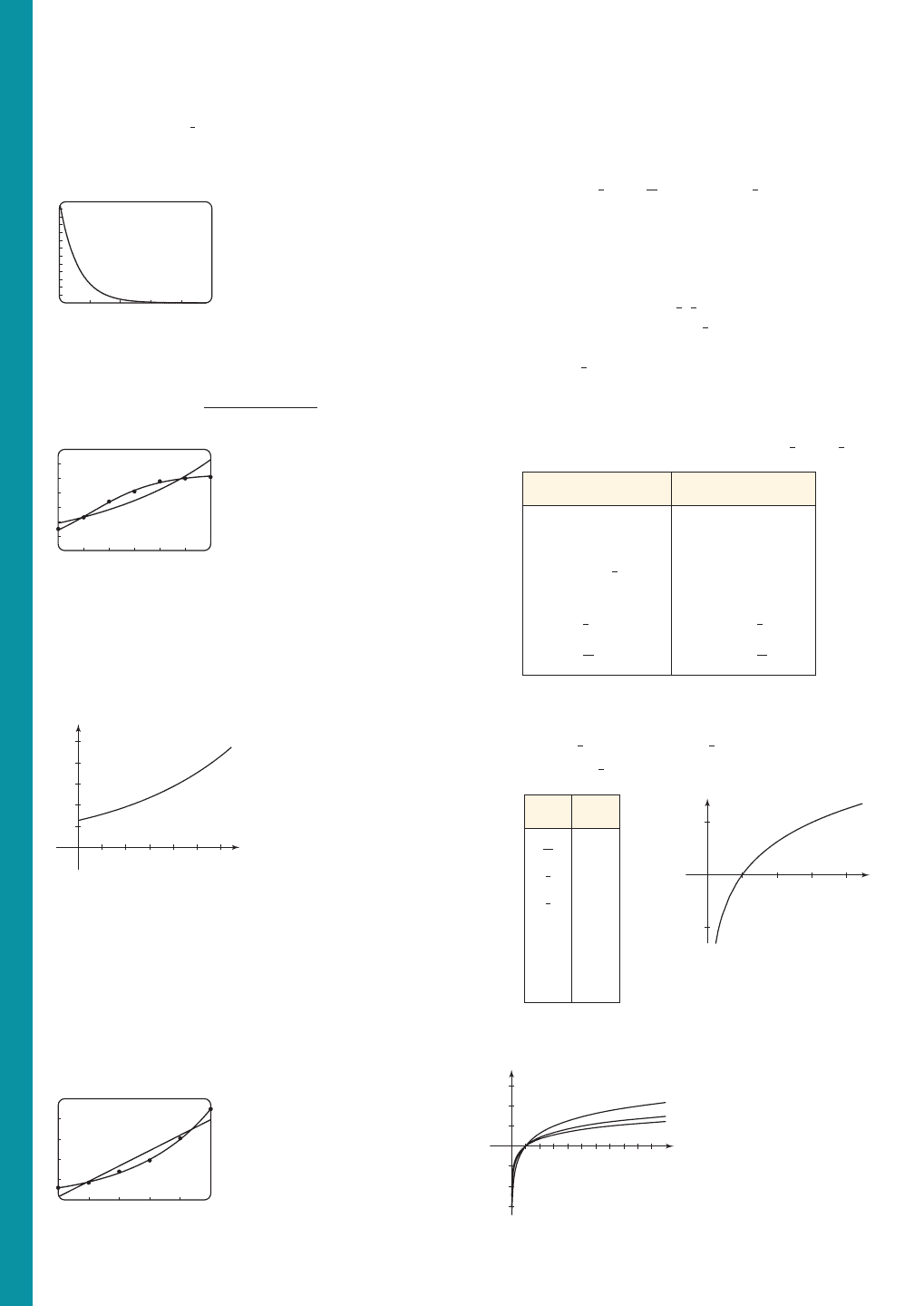
x
f 1x 2
1
27
- 3
1
9
- 2
1
3
- 1
1 0
3 1
9 2
27 3
Logarithmic form Exponential form
log
8
8 = 1
8
1
= 8
log
8
64 = 2
8
2
= 64
log
8
4 =
2
3
8
2>3
= 4
log
8
512 = 3
8
3
= 512
log
8
A
1
8
B=-1 8
-1
=
1
8
log
8
A
1
64
B=-2 8
-2
=
1
64
A24 Answers to Selected Exercises and Chapter Tests
27. (a) (b)
(c)
(d)
1.4 * 10
-6
mg
A1t 2= 65010.435 2
t
A1x 2= 650A
1
2
B
x
650
10
0
29. Plan A: $8454.54, Plan B: $8353.55; Plan A is better.
70
g
f
6
0
(c) The exponential model predicts 8.2 billion turtles in
100 years, while the logistic model predicts 51 turtles. The
logistic model seems more reasonable.
Chapter 3 Test
■
page 311
1. (a) 640 (b) 1.5; 50% (c) 7290
(d)
31. (a) Logistic
(b) Exponential model: f 1t2= 19.0311.2200612
t
(e) 17.086; 2. (a) $2024.11 after
4 months, $2073.20 after 1 year, $2227.74 after 3 years.
(b) No 3. (a) Average rate of change: 2; percentage rate of
change: 800% (b) Average rate of change: 18; percentage rate
of change: 800% 4. (a) A logistic growth model (b) 125
(c) 457 (d) No, the carrying capacity is 500. 5. Graph A:
graph of h; graph B: graph of g; graph C: graph of f ; graph D:
graph of k 6. (a) (i)
(ii)
(b) (c) The exponential model
fits the data better. The
mass in week 6 is predicted
to be 13.6 kg.
g1x2= 1.182673911.502042
x
f 1x 2= 0.30952 + 1.52286x
P1t 2= 640117.086 2
t
10
5
g
f
0
0
500
1000
1500
2000
2500
1.00.5 2.01.5 3.0
2.5
y
x
Chapter 4
Algebra Checkpoint 4.1
■
page 330
1. (a) 64 (b) (c) (d) 2 (e) 2. (a) (b)
(c) (d) (e) 3. (a) (b) (c)
(d) (e) 4. (a) (b) (c) (d)
(e)
4.1 Exercises
■
page 331
1. x; 3, 2, 1, 0, , , , , 2. (a)
(b) 3. 9; 1, 0, , 2, 4. (a) II (b) I
5. (a) True (b) True (c) False 7. (a) 4 (b)
(c) (d) 9. (a) 2.121 (b) 3.699 (c) 0.151
(d) 11. (a) (b) 2.238 13. (a) 0.602
(b) 3.736 15. (a) 1 (b) 0 (c) 2 17. (a) 2 (b)
(c) 1 19. (a) 4 (b) 3 (c) 2 21. (a) 37 (b) 8 (c) 5
23. (a) 5 (b) 17 (c) 0 25. (a) 3 (b) (c)
27.
1
4
1
2
- 1
- 3.921- 0.523
1
3
- 2
- 1
1
2
- 15
2
= 25
log
5
125 = 3
3
4
1
2
- 3- 2- 1
9
-1>2
9
1>2
9
-1
9
3
9
2
2
-1>3
2
-4
2
-1
2
6
2
4
10
-1>2
10
-2
10
-1
10
4
10
2
1
3
1
25
1
5
41.
29. (a) (b) 31. (a)
(b) 33. (a) (b)
35. (a) (b) 37. (a) 32
(b) 4 39. (a) (b) 16
1
2
log
2
A
1
8
B=-3log
8
A
1
8
B=-1
log
10
0.0001 =-4log
3
27 = 39
1>2
= 3
8
1>3
= 25
0
= 15
3
= 125
1
0
1
y
x
43. III 45. IV 47. 49.
51.
a = 3a = 5
1
a=
3
a=
5
a=
7
0
1
y
x
Logistic model: g1t 2=
52.86
1 + 2.68e
-0.76425t
The graphs all intersect at the point .11, 02
Answers to Section 4.4 A25
4.2 Exercises
■
page 339
1. sum; 2, 3 2. difference; 2, 3 3. times; 4. 10;
Change of Base; 5. (a) III
(b) I (c) II 6. Change of Base; 13 7. (a) False
(b) True (c) True (d) False (e) False (f) False
(g) False (h) True 8. They are the same. 9. (a) 2
(b) 5 (c) 11. (a) (b)
13. (a) (b)
15. (a) (b)
17. (a) (b)
19. (a) (b)
21. (a) (b)
23. (a) (b)
25. 5 27. 15 29. 3 31. 2 33. (a) 2.321928
(b) 0.430676 35. (a) 0.493008 (b) 3.503061
37. (a) (b)
log
x
4
1x - 12
2
2
3
x
2
+ 1
log
4
B
y + 1
y - 1
log
3
a
12x - 12
4
x + 1
blog
2
1A
3
1B + 12
2
2
log
6
y
4
2z
4
log
2
AB
C
2
2 log
5
x - log
5
y - 3 log
5
z10 log x + 10 log y
3 log r + 4 log s -
1
4
log t2 log
2
s +
1
2
log
2
t
-
1
2
log zlog
2
A + 2 log
2
B
log
3
x - 3 log
3
y1 + log
2
x- 3
log
7
12 =
log
10
12
log
10
7
L 1.277
10
#
2
1.5
_1.0
10
0
1.0
_0.8
10
0
39. 41.
The graphs all intersect at The graph of
. is the graph of
shifted upward by log c units.
f 1x 2= log x11, 02
G1x 2= log1cx 2
3.2
_2.2
10
a=2
a=4
a=6
0
5
_2
10
c=4
c=3
c=2
c=1
0
4.3 Exercises
■
page 347
1. logarithm; 3, 2. lower 3. higher
4. 1000 5. 990; 2
7. 9.
- 2
40123
log of weight (in oz)
Smallest primate Monkey Gorilla
2010 12 14 16 18
log of number of:
Stars in
Andromeda
galaxy
Cells in
human
body
Atoms in
drop of
water
11. (a) 2.30 (b) 3.49 13. (a)
(b) 15. (a) 91 dB (b) 99 dB
17. (a) California red: ; Italian white:
(b) California red 19. (a) 6.7; yes1.58 * 10
-3
M
1.58 * 10
-4
M
3.16 * 10
-7
M
2.51 * 10
-3
M
(b) Lower 21. (a) 105 dB (b) 85 dB 23. 8.2
25. 2 times more intense 27. (a)
29. For , ; for ,
4.4 Exercises
■
page 358
1. (a) natural, 2.71828 (b) e; 1 2. principal, interest rate,
time in years, account value; $112.75 3. ln a, 0.405
4. 5. The one that doubles every 10 minutes
6. Both grow at the same rate. 8. (a) (b)
(c) (d) 9. (a) 8.155 (b) 4.055
(c) 0.135 (d) 19.778
11.
A1t 2= e
t
A1t 2= 2
t
A1t 2= 2
t
A1t 2= t
f 1t 2= Ce
rt
ID = 4.32W = 10 mmID = 5.32W = 5 mm
M = 2.5 log B
0
- 2.5 log B
y
0x
1
fg
4
13. (a) 4 (b) (c) 0.693 (d) 4.669
15. 17.
- 1
1
0
2
y
x
4
_2
10
a=2
a=e
a=4
0
19. I 21. III 23. (a) Growth (b) 0.50 25. (a) Decay
(b)
27. (a) 29. (a)
(b) (b)
f 1x 2= 1000e
-0.36x
f 1x 2= 1000e
0.024x
- 0.30
0
1000
2000
3000
4000
5000
20 40 60
y
x
0
200
600
400
1000
800
1200
13254
y
x
31. (a) ; 0.693 (b) ;
33. 100; 0.693 35. (a)
(b) (c) The graphs are the same.
37. (a) (b)
(c) The graphs are the same. 39. (a)
(b) (c) The graphs are the same.
41. (a) (b)
(c) The graphs are the same. 43. (a) $35,264.97
(b) $35,369.45 (c) $35,440.63 (d) $35,476.69
45. (a) 0.10 (b) $18,135.93 (c) $18,024.78
47. (a) 500 bacteria (b) Increasing; 45% (c) 1928
g1t 2= 3000e
-0.1386t
f 1t 2= 300010.87062
t
g1t 2= 3000e
0.1022t
f 1t 2= 300011.10762
t
g1t2= 200e
-0.056t
f 1t 2= 20010.9462
t
g1t2= 200e
0.033t
f 1t 2= 20011.0342
t
- 0.693
g1x 2= 2500e
-0.693x
f 1t 2= 2500e
0.693t
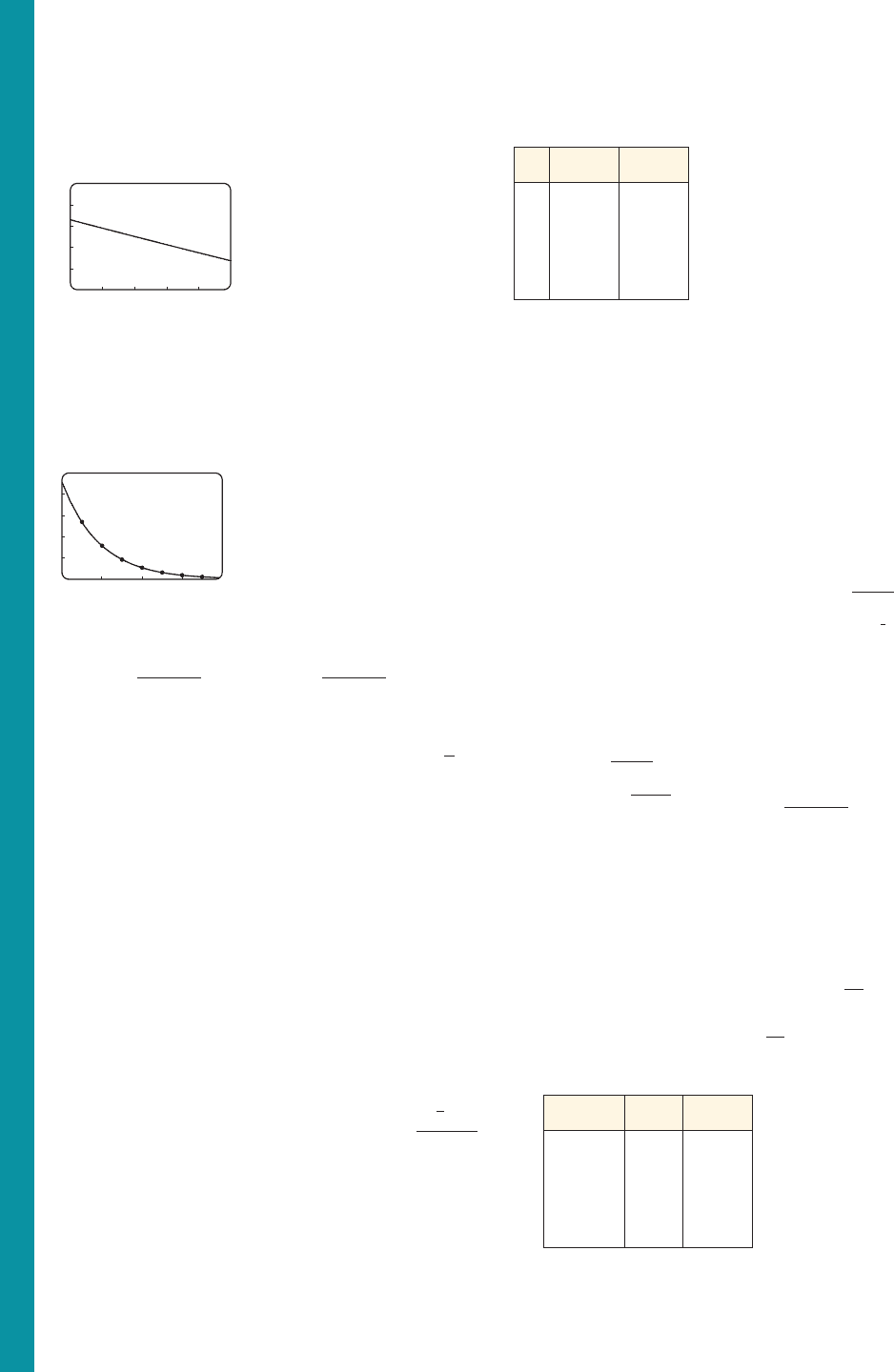
x
g1x 2 f 1g1x 22
12,000 400 7,600
24,000 800 15,200
36,000 1200 22,800
50,000 1667 31,673
100,000 3333 63,327
A26 Answers to Selected Exercises and Chapter Tests
49. (a) ; decreasing (b)
(c)
f 1t 2= 383,000e
-0.0052t
- 0.52%
400,000
350,000
1000
51. (a) ; (b) ;
(c) The graphs are the same. 53. (a) ;
(b) ;
(c) 462.9 million; yes 55. (a)
(b) (c) (d) 22.8 lm
(e)
k = 0.1062I1x2= 22.759e
-0.1062x
I1x 2= 22.75910.8992 2
x
g1t 2= 22.5e
0.3024t
r = 0.3024f 1t2= 22.511.35312
t
a = 1.3531
g1t 2= 20e
1.386t
r = 1.386f 1t2= 2014 2
t
a = 4
25
40
0
4.5 Exercises
■
page 373
1. (a) (b) (c) 3.2189
2. (a) (b) (c) 3
3. Base 2 5. 1.398 7. 9. 0.178 11. 0.092
13. 1.363 15. 2.771 17. 6.213 19. 0.805 21.
23. 0.562 25. 27. 1024 29. 10,000 31.
33. 1004 35. 24.5 37. 4 39. 5 41. 2.21 43.
45. 0, 1.14 47. 0.36 49. (a)
(b) $6561.75 (c) 6.4 yr 51. (a) 11.6 yr (b) 14.1 yr
53. (a) (b) (c) 1823 (d) 11.18 h
(e) 0.58 h 55. (a) (b)
(c) 24.2 yr (d) 2011 57. (a)
(b) 1.16 h 59. (a) (b)
(c) 0.92 h (55 min) 61. (a)
(b) (c) 3.94 g (d) 467 yr
63. 80,089 yr 65. 3029 yr 67. (a) 1938 yr
4.6 Exercises
■
page 386
1. 12 2. Multiply by 2, then add 1; add 1, then multiply by 2.
, , ,
3. different; Horizontal Line 4. (a) one-to-one;
(b) 5. Take the third root, subtract 5, then
divide by 3. (a) (b)
6. 7. Linear; linear 8. (a) False (b) True
9. (a) 5 (b) 2 11. (a) 5 (b) 2
ln x
f
-1
1x 2=
1
3
x - 5
3
f 1x 2= 13x + 52
3
g
-1
1x 2= x - 2
g
N1x 2= 21x + 1 2M1x 2= 2x + 1g1x 2= 2xf 1x2= x + 1
m1t 2= 2210.99957 2
t
a = 0.99957
62.8°CT = 20 + 80e
-1.4988t
T = 65 + 147e
-2.895t
f 1t 2= 70.711.0292
t
a = 1.029
f 1t 2= 15e
1.2t
r = 1.2
A1t 2= 600011.01125 2
4t
- 0.57
1
32
- 9.113
- 0.585
- 1.159
1 =
31x - 22
x
log a
31x - 22
x
b= 0
x = ln 25e
x
= 25
x
f 1g1x22 g1f 1x 22
1 2 3
2 4 3
3 2 5
4 5 5
5 2 1
13.
15. (a) M(x): Multiply by 3, then add 2. N(x): Add 2, then
multiply by 3. (b) ;
(c) ; 17. (a) M(x): Subtract 1, square,
then multiply by 2; N(x): Square, multiply by 2, then subtract 1.
(b) ; (c) ;
19. (a) M(x): Add 3, then raise e to that result;
N(x): Raise e to the input, then add 3. (b) ;
(c) ;
21. (a) M(x): Take the natural log, multiply by 3, then add 5;
N(x): Multiply by 3, add 5, then take the natural log.
(b) ;
(c) is not defined. 23. (a) Add 6, M132= 8.296; N1- 22
N1x 2= ln13x + 5 2M1x2= 3 ln x + 5
N1- 22= 3.135M
13 2= 403.43N1x2= e
x
+ 3
M1x 2= e
x + 3
N1- 22= 7
M132= 8N1x 2= 2x
2
- 1M1x2= 21x - 12
2
N1- 22= 0M132= 11
N1x 2= 31x + 2 2M1x 2= 3x + 2
then divide by 3. (b) ;
25. (a) Multiply by 2, then subtract 4. (b) ;
27. (a) No inverse (b)
29. 2 31. 3 33. (a) 12 (b) 2 (c) 4 (d) 5
35. (a) 6 (b) 4 (c) 0 45. One-to-one
47. Not one-to-one 49. One-to-one 51. One-to-one
53. Not one-to-one 55. Not one-to-one
57. 59.
61. 63.
65. 67.
69. 71. Not one-to-one 73. One-to-one
75. Not one-to-one 77. (a) (b) ;
(c) ; ;
gives the lower price. 79. (a)
(b) (c) ; gives the
number of pounds of emitted when x miles are driven.
(d)
CO
2
f 1g1x22f 1g1x22= 19 a
x
30
bf 1x 2= 19x
g1x 2=
x
30
g1f 1x22
g1f 1x22= 0.8x - 50f 1g1x 22= 0.81x - 502
g1x 2= x - 50f 1x2= 0.8x
f
-1
1x 2= e
x
+ 3
f
-1
1x 2= 2 ln xf
-1
1x 2= 2
x
- 1
f
-1
1x 2=
21x + 12
1 - x
f
-1
1x 2= 2
3
x + 4
f
-1
1x 2= 2xf
-1
1x 2=
x - 7
4
f 1x 2=-2x
2
+ 3f
-1
1x 2= 2x - 4
f 1x 2=
1
2
1x + 42
f
-1
1x 2=
x + 6
3
f 1x 2= 3x - 6
Answers to Section 5.1 A27
81. (a) (b)
(c) (d) ;
the sticker price when x is the purchase price (e) $16,294; the
sticker price of a car with a purchase price of $13,000
83. (a) ; the number of years
since 1990 as a function of the population (b) 1998
85. (a) ; x represents volume, and
represents time. (b) 24.5; the tank has 15 gallons left after
24.5 minutes
Chapter 4 Review Exercises
■
page 395
1. (a) 2 (b) (c) 3 (d)
3.
- 3- 3
F
-1
F
-1
1x 2= 40 - 41x
f
-1
1x 2= 32.761ln x - 6.7412
H
-1
1x 2=
x
0.85
+ 1000H1x 2= 0.851x - 1000 2
g1x 2= x - 1000f 1x2= 0.85x
1
0
1
y
x
5. (a) 1.8394 (b) 9.9658 (c) 1.9731 (d) 2.5177
7. (a) (b) (c)
9. (a) (b)
11. (a) (b)
13.
ln
x + 1
y
2
log
2
1X
3
Y2
log 5 + log x - 2 log ylog
2
3 + log
2
a + log
2
b
e
4
= y2
3
= x5
2
= 25
15. ; this is less than 7.
17.
pH = 1.14
1
0
1
y
x
y
0x
5
1
19. 21. 23. 1f 1t 2= 1500e
1.0986t
f 1t 2= 2400e
1.0986t
25. 3.3922 27. 29. 31. (a) ;
(b) 10;
33. (a) ; (b) 128; 5832
35. 37. 39. One-to-onef
-1
1x 2= ln
x
8
f
-1
1x 2=
x + 7
3
g1f 1x 22= 8x
6
f 1g1x22= 2x
6
- 29g1f1x 22= 6x - 11
f 1g1x22= 6x - 2
48
31
1
9
Chapter 4 Test
■
page 400
1. (a) (b) (c) 100
2. (a)
3
2
- 2
3. (a) (b)
4. (a) 6.4 (b) 5. (a) $2543.95 (b) $2540.10;
investment (a) is better. 6. (a) ;
(b) 299 s 7. (a) 0.56 (b) 4 8. (a)
(b) ; the number of books as a function of the
shipping fee (c) 11 books 9. (a) ;
(b) is not defined;
Chapter 5
5.1 Exercises
■
page 422
1. (a) up (b) left 2. (a) down (b) right 3. (a) x-axis
(b) y-axis 4. (a) II (b) IV (c) I (d) III 5. Shift to the
right 4 units, then upward 5 units. 6. Reflect in the x-axis and
in the y-axis, then shift upward 6 units.
7. (a) (b)
g1f 1022= 1.9956
f 1g1022g1f 1x22= log110
x + 2
- 12
f 1g1x22= 1001x - 12
S
-1
1x 2= x - 1.95
S1x 2= 1.95 + x
- 0.0231A1t2= Ce
-0.0231t
5.01 * 10
-5
ln
5x
2
x
3
+ 7
log 5 + 4 log x - log16x - 112
x 0.1 0.5 1 3 5
f 1x 2 - 2.10
- 0.63
0 1 1.47
(b)
1
0
1
y
x
41. (a) (b) (c) No;
after 17.8 hours (d) ; (e) 42.5 mg
(f) (g) No 43. (a) 6.4; yes
(b) 45. (a) 4.25% (b) $283,996.22
(c) $283,248.88 47. (a) 6 yr (b) ; 0.1155
(c) 2016 (d) 2,386,872 lb; logistic 49. (a) ;
(b) represents taking the $2 discount
first, then the 5% discount; represents taking the 5%
discount first, then the $2 discount. (c) ;
(d) $36.10; $36.00; yesg1f 1x22= 0.95x - 2
f 1g1x22= 0.951x - 22
g1f 1x 22
f 1g1x22g1x2= x - 2
f 1x 2= 0.95x
W1t 2= 23e
0.1155t
1.26 * 10
-6
M
S1t 2= 122.6e
-0.0263t
- 0.0263N1t 2= 80e
-0.0263t
N1t 2= 8010.974 2
t
M1x 2= 8010.9 2
x
y
0x
1
2
y
0x
1
4
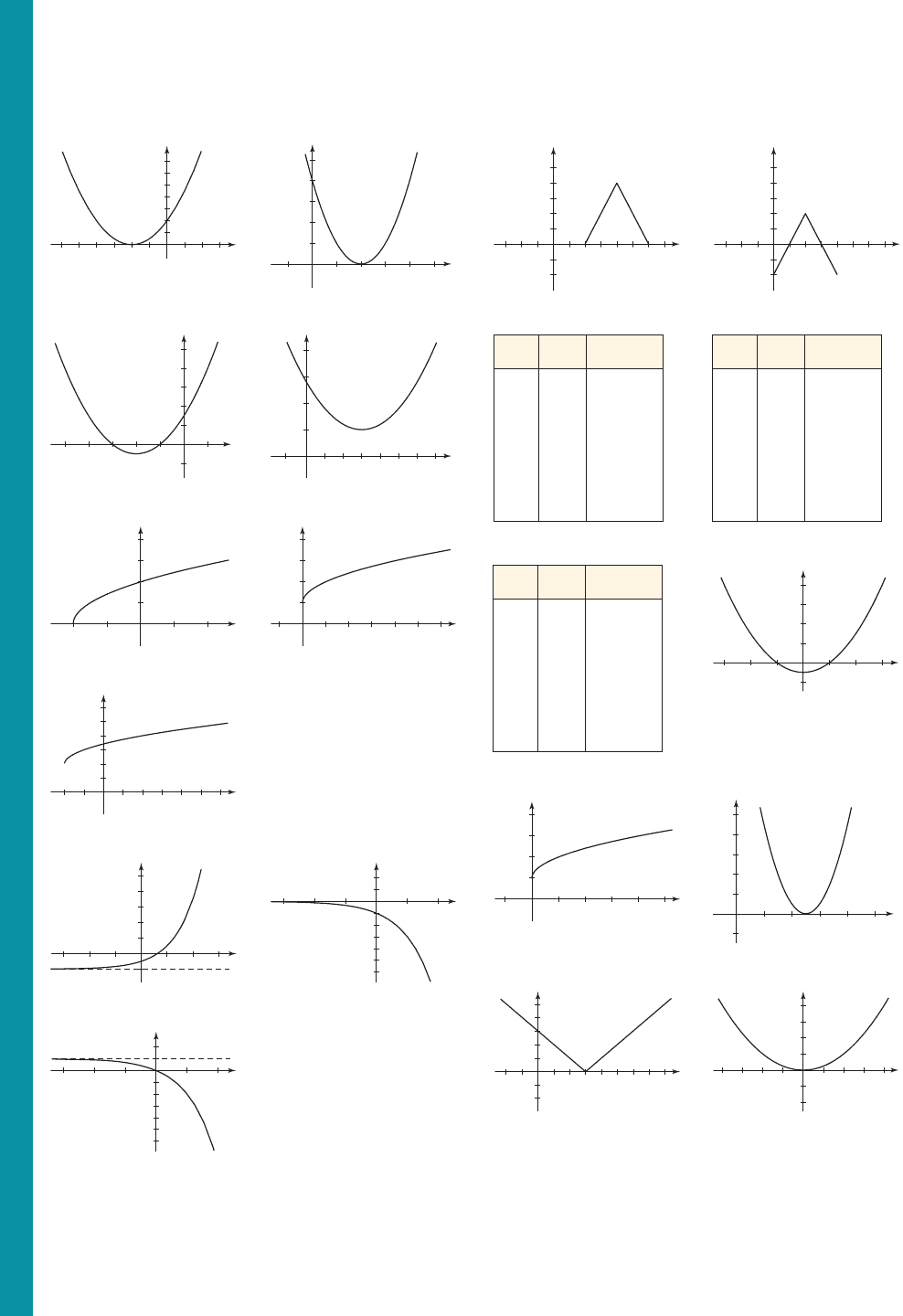
A28 Answers to Selected Exercises and Chapter Tests
17. (a) (b)9. (a) (b)
y
x
1
4
0
0
4
2
y
x
11. (a) (b)
0
2
1
y
x
0
5
1
y
x
13. (a) (b)
y
0x
2
1
y
0x
1
1
y
0x
1
1
15. (a) (b)
y
0x
1
2
y
x
1
2
y
x
1
2
0
x
y
1
1
0
x
y
1
1
0
19. 21.
x
f 1x 2 f 1x 2ⴙ 1
- 3
20 21
- 2
27 28
- 1
53 54
0 42 43
1 39 40
2 70 71
3 21 22
x
f 1x 2 f 1x ⴙ 2 2
- 6
105 99
- 4
99 82
- 2
82 53
0 53 20
2 20 6
4 6 2
6 2 —
x
f 1x 2 f 1ⴚ x 2
- 6
105 2
- 4
99 6
- 2
82 20
0 53 53
2 20 82
4 6 99
6 2 105
23. 25.
(c)
y
x
1
2
27. 29.
y
0x
1
1
31. 33.
0
2
2
y
x
y
0x
1
1
y
0x
1
1
(c)
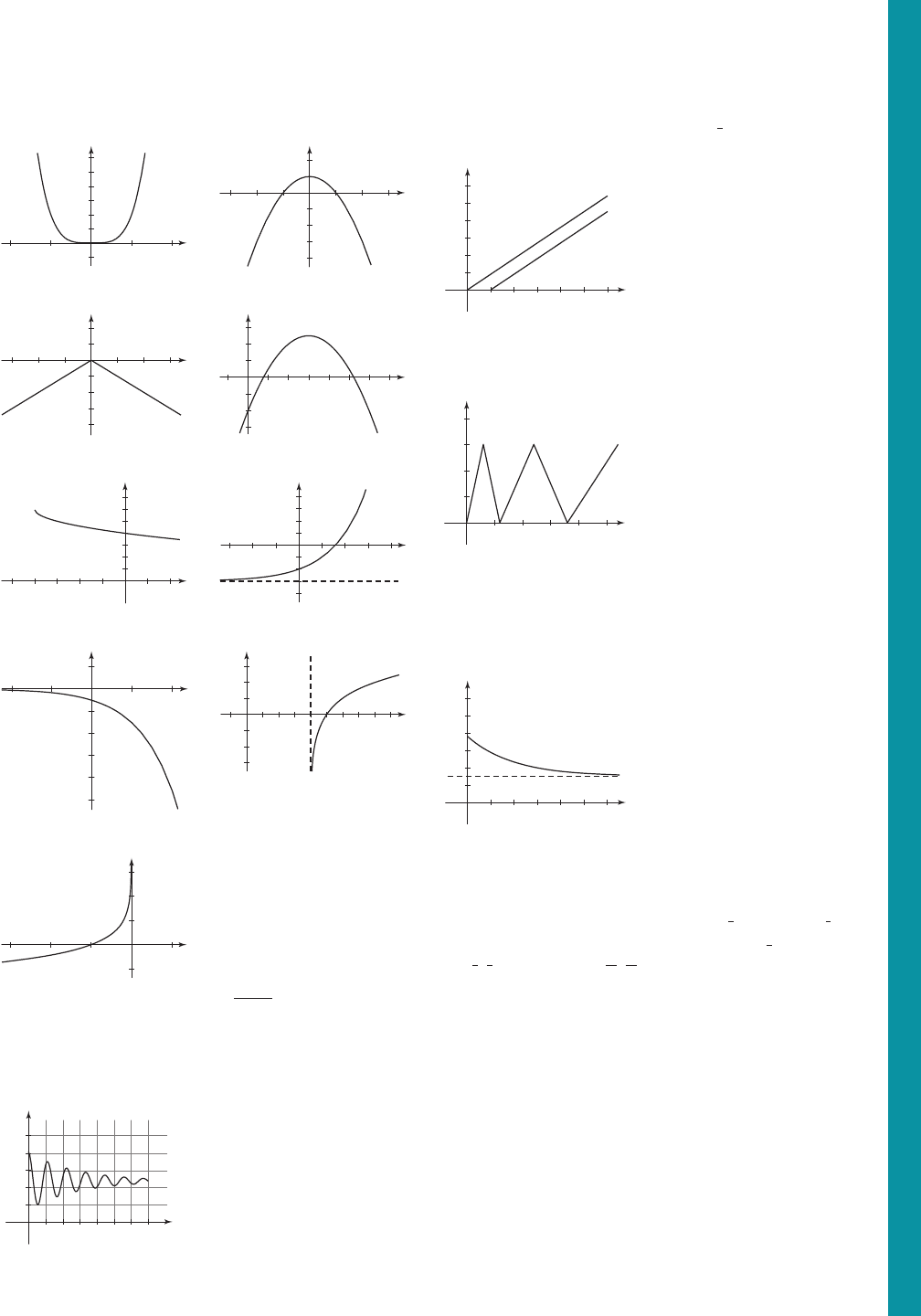
Answers to Section 5.2 A29
47. 49.
35. 37.
39. 41.
43. 45.
y
0x
1
1
y
0x
1
2
51.
y
x
1
1
y
x
1
0
2
y
x
1
1
0
y
0x
2
1
x
y
1
2
y
x
1
1
y
0x
1
2
53. 55.
57. 59.
61. 63. 65. (a)
Luisa
drops to 200 ft, bounces up and down a bit, then settles at 350 ft.
(b) (c) H1t2= h1t 2- 100
g1x 2=-2
x
- 1g1x2= 1x - 22
2
f 1x 2= 2
x
- 2f 1x 2= 0 x - 3 0+ 1
f 1x 2= 1x + 2
f 1x 2= x
2
+ 3
t (s)
y
(ft)
500
4
0
67. (a) (b)
(c)
Shift the graph of d to the
right 0.5 unit to get the
graph of D.
D1t 2= 90At -
1
2
Bd1t 2= 90t
0
50
100
150
200
250
300
0.5 1.0 1.5 2.0 2.5 3.0
y
t
D
d
69. (a) She swam two and a half laps, slowing down with each
successive lap; 1.67 m/s
(b)
This graph is a vertical
stretching of the original
function by a factor of 1.2.
0
20
40
60
80
25020015050 100
y
t
(c) 2 m/s
71. (a) (b) The graph of is a vertical
stretching of the graph of f by a factor of 5;
73. (a) Stretch vertically by a factor of 115, then shift upward
75 units.
(b)
g1t 2= 5011.05 2
t
gf 1t2= 1011.05 2
t
0
250
300
150
50
200
100
605040302010
y
t
Algebra Checkpoint 5.2
■
page 435
1. (a) (b) (c)
(d) 2. (a) Yes (b) No (c) Yes (d) No
3. (a) (b) (c) (d)
4. (a) 25; 5 (b) 100; 10 (c) 27; 3 (d) 25; 5. (a) 9; 9
(b) ; (c) 4; 8 (d) ;
5.2 Exercises
■
page 435
1. square 2. (a) h, k (b) upward (c) downward
3. upward; 3, 5 4. downward; , 5 5. (a)
(b) 8 6. (a) (b) mn (c) 15
7. (a) Yes (b) No (c) No 9.
11. 13.
15.
17. (a) (b) (3, 4)
19. (a) (b)
21. 23. f 1x2= 21x + 52
2
- 49f 1x 2= 1x + 12
2
- 6
11, - 32f 1x 2= 21x - 12
2
- 3
f 1x 2=-1x - 32
2
+ 4
f 1x 2= 100x
2
+ 120x + 43
f 1x 2= x
2
- 2x + 6f 1x 2= 4x
2
- 25
f 1x 2= 8x
2
+ 10x - 3
x
2
- 1m + n2x + mn
x
2
- 6x + 8- 3
1
12
1
36
1
4
1
4
5
2
As +
5
2
B
2
Aw -
1
2
B
2
1t - 82
2
1x + 72
2
36 - 9√
2
6r
2
- 13r + 62t
2
- 3t - 5x
2
- x - 6
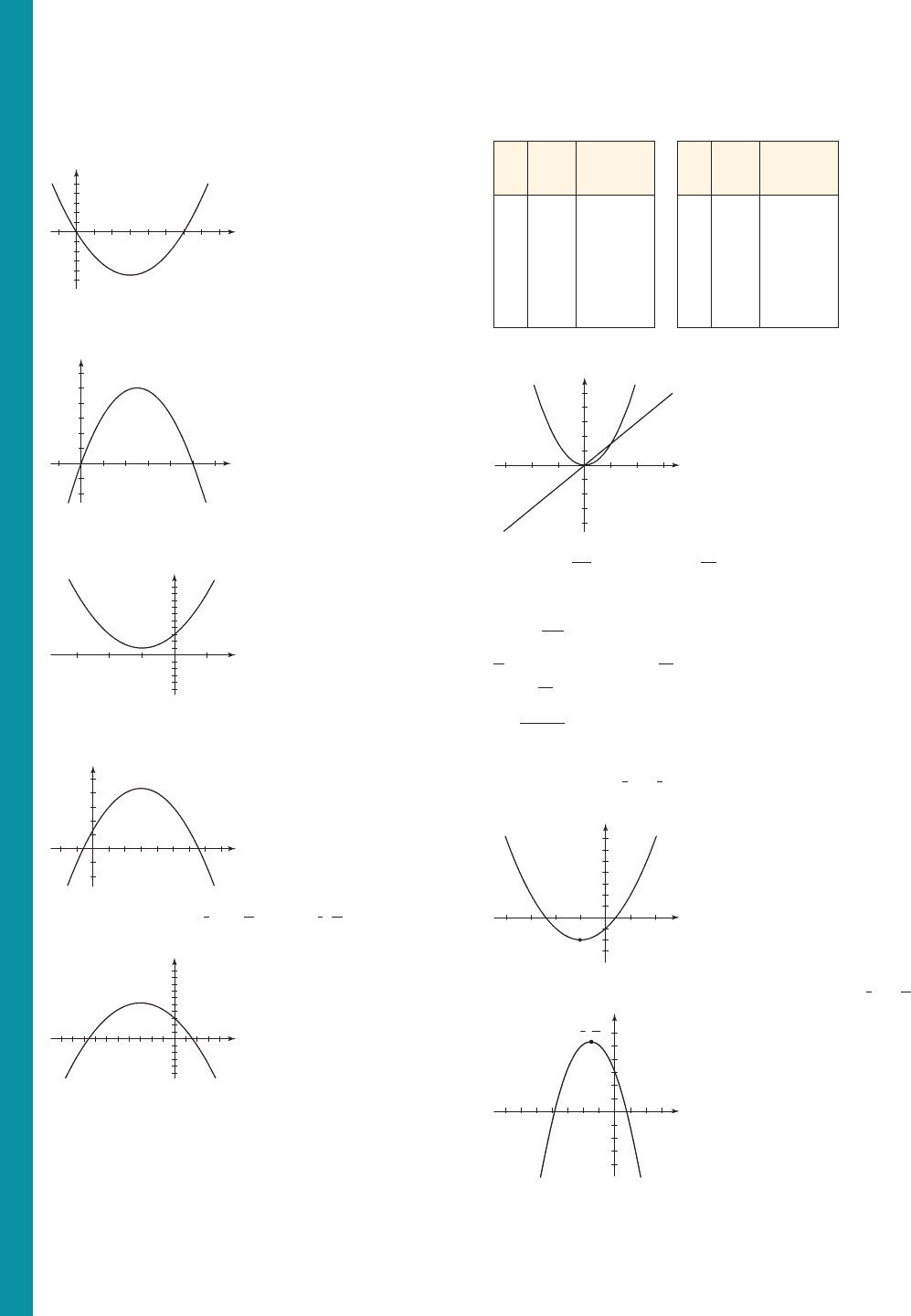
A30 Answers to Selected Exercises and Chapter Tests
25. (a) (b)
(c)
13, - 92f 1x2= 1x - 32
2
- 9
29. (a) (b)
(c)
1- 1, 12f 1x 2= 21x + 12
2
+ 1
35. 37.
39. 41. f 1x2=-1x + 22
2
+ 5f 1x 2= 1x - 12
2
+ 2
f 1x 2=-31x - 32
2
+ 4f 1x2=-51x + 22
2
- 3
y
x
1
6
27. (a) (b) (5, 25)
(c)
f 1x 2=-1x - 52
2
+ 25
0
5
2
y
x
y
x
1
0
5
31. (a) (b) (3, 13)
(c)
f 1x 2=-1x - 32
2
+ 13
y
x
1
0
3
33. (a) (b)
(c)
A-
3
2
,
21
4
Bf 1x 2=-Ax +
3
2
B
2
+
21
4
y
x
2
0
5
x
f 1x 2
Rate of
change
0 0 —
1 3 3
2 6 3
3 9 3
4 12 3
5 15 3
x
g 1x 2
Rate of
change
0 0 —
1 3 3
2 12 9
3 27 15
4 48 21
5 75 27
(b)
y
0x
f
g
1
2
45. 47.
5.3 Exercises
■
page 444
1. (a) (b) minimum (c) maximum 2. (a) minimum;
, (b) maximum; , 23 3. (a) (b) up
(c) 4. (a) (b) up
(c) (d) 1 5. (a) Minimum; 3 (b) 2
m + n
2
x
2
- 1m + n2x + mn- A
- 6
2
B= 3
x
2
- 6x + 8
12
- 4
- 13
12
4
- b
2a
f 1x 2=
1
600
x
2
f 1x 2=
1
100
x
2
y
x
1
1
0
(_1, _2)
y
x
3
3
()
_,
3
2
21
4
0
17. (a) (b) Maximum: f A-
3
2
B=
21
4
43. (a)
7. (a) Maximum; 5 (b) 4 9. Maximum:
11. Minimum: 13. Minimum:
15. (a) (b) Minimum: f 1- 12=-2
h 1- 22=-8f A-
1
2
B=
3
4
f 13 2= 10
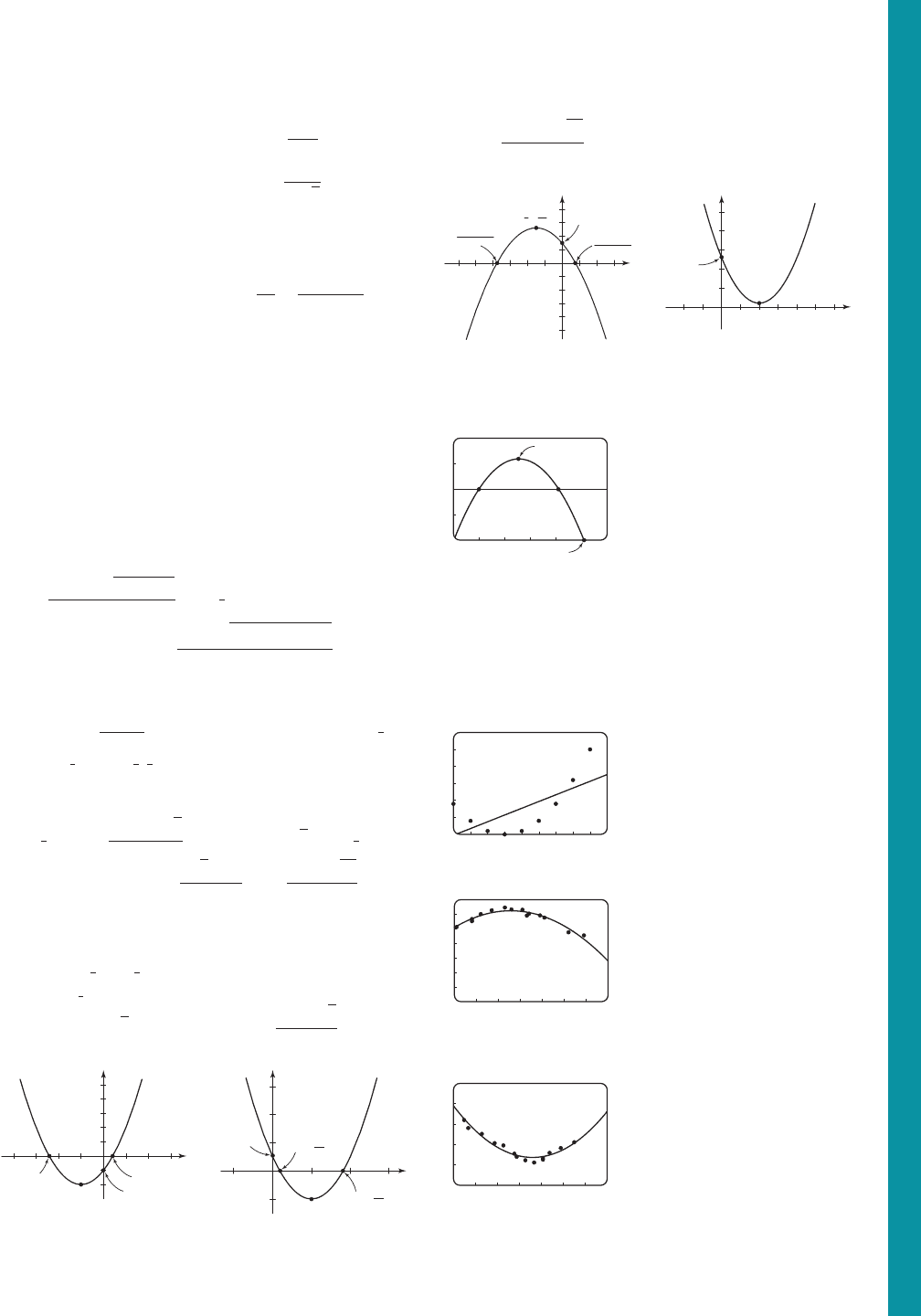
Answers to Section 5.5 A31
19. (a) (b) Minimum value:
21. (a) 1.18 (b) Maximum value:
23. 7.34 m; 1.22 s 25. 22,500; 50
27. (a) (b) ;
600 ft by 1200 ft 29. (a)
(b) 300 ft by 300 ft 31. (a)
(b) 5 cm 33. (a)
(b) $9.50
Algebra Checkpoint 5.4
■
page 456
1. (a) (b) (c)
(d) 2. (a)
(b) (c)
(d) 3. (a)
(b) (c) (d)
4. (a) (b)
(c) (d)
5.4 Exercises
■
page 456
1. (a) (b) , , ; 4 or
2. (a) 5, 1; 5 or (b) ; 5 or
3. (a) 2 (b) 1 (c) 0 4. (a) 1 and 5 (b) positive
(c) 1 and 5 5. (a) upward (b) 2, 4 (c) 3 6. (a) upward
(b) m, n (c) (d) 4 7. 4, 3 9. 3, 4 11. , 2
13. , 15. , 17. (a) 3, 5
(b) 19. (a) , 1
(b) 21. , 5 23. 2, 5- 3f 1x 2=-3x
2
- 9x + 12
- 4f 1x 2= x
2
- 8x + 15
1
2
-
4
3
-
1
2
- 3
-
1
3
m + n
2
- 1
4 ; 216 - 41121- 52
2112
- 1
- 2- 4- 1
1
2
- b ; 2b
2
- 4ac
2a
12u - 3213u + 1 212s - 321s + 12
1t - 421t + 3 21x + 221x + 32
1u + 72
2
13r - 42
2
1t - 62
2
1x + 42
2
321w - 22- 74321w - 22+ 74
1u + 721u - 5 241t + 221t - 22
1x + 621x - 6 213r + 42312r + 32- 54
1x + 12321x + 12+ 142t12t - 3 2x1x + 1 2
R1x 2= 110 - x2127,000 +
3000x2
A1x 2=
x
2
16
+
110 - x 2
2
16
A1x 2= x1600 - x 2
720,000 ft
2
A1x 2= x12400 - 2x 2
f a- a
- 1
222
bb = 1.17677
f a-
1.79
2
b=-4.011025- 4.01
y
x
1
0
_1+Ϸ2
_1-Ϸ2
_1
(_1, _2)
1
x
y
1
4
1
0
1-
Ϸ
(1, _2)
6
3
1+
Ϸ
6
3
57. (a) 59. (a) None
(b) (b)
- 3 ; 221
2
x
y
2
3
2
_3+
_
œ∑∑
,
()
21
2
21
4
3
2
_3-
œ∑∑
21
2
61. (a) 0.53 s and 1.92 s (b) No (c) 2.45 s
63. (a) After 0.99 s and 4.1 s (b) After 2.55 s (c) After 5.1 s
(d)
x
1
(2, 1)
13
5
0
y
40
6
y=20
Highest point
Hits
g
round
0
65. (a) (b) 90 ft by 130 ft
67. (a)
(b) $19.00 (c) $6.87 or $12.13
5.5 Exercises
■
page 464
1. scatter plot 2. quadratic 3.
4. y =-0.33 + 2x
y = x
2
- 6x + 9
R1x 2= 110 - x2127,000 + 3000x2
A1x 2= x1x + 40 2
30
9
0
120
50
7
0
(b) (c) 77.9
7. (a)
y =-1.7529x
2
+ 8.983x + 100.89
5. (a)
(b) (c) 56.4y = 1.9575x
2
- 14.082x + 59.011
70
20
7
0
25. , 1 27. 29. 31.
33. No real solution 35. 37.
39. , 0.259 41. No real solution 43. (a) 32; 2
(b) 2 45. (a) 0; 1 (b) 1 47. (a) ; 0
(b) None 49. (a) (b) Positive (c)
(d) 51. (a) 3 (b) Zero (c) 3
(d) f 1x2=
1
3
x
2
- 2x + 3
f 1x 2=-
1
2
x
2
-
1
2
x + 1
- 2, 1- 2, 1
- 64
- 0.248
8 ; 214
10
25
; 1
2
3
4
- 6 ; 327
- 3 ; 25
2
-
3
2
53. (a) 55. (a)
(b) (b)
3 ; 26
3
- 1 ; 22

10
_2
4
0
41. (a) The y-intercept (b) The x- and y-coordinates of the
vertex (c) The x-intercepts (d) Factored form;
(e) Standard form;
(f) General form;
(g) Maximum: ; minimum: ; minimum:
f 1- 12=-22
f 14 2=-6f A
7
2
B=-
9
2
f 1x 2= 3x
2
+ 6x - 19f 1x 2=
3
8
1x - 42
2
- 6
f 1x 2=-21x - 221x - 52
A32 Answers to Selected Exercises and Chapter Tests
9. (a)
6000
0
40
10
15
4
0
(b) (c) 5114 kg/acre
11. (a)
y =-12.627x
2
+ 651.55x - 3283.2
(b)
(c) 0.33 s and 2.91 s (d) 14.08 ft
y =-4.875x
2
+ 15.797x + 1.2845
Chapter 5 Review Exercises
■
page 468
1. 3.
y
x
g
f
2
0
1
5. 7.
9.
y
x
g
f
2
0
1
y
x
g
f
1
0
2
y
x
1
0
2
0
1
1
y
x
11. (a) (b)
(c)
, 2;
13. (a) (b)
(c) (d) 10
1- 3, - 92f 1x2= 1x + 3 2
2
- 9
- 8- 4
f 1x 2= 1x + 12
2
- 9f 1x2= x
2
+ 2x - 8
y
x
1
2
15. (a) (b) (2, 9)
(c) (d) 0
f 1x 2=-1x - 22
2
+ 9
17. (a) (b)
(c) (d) 1
A1, -
7
2
Bf 1x 2=
1
2
Ax - 1B
2
-
7
2
y
x
1
0
2
19. 21.
23. Minimum: 25. Maximum:
27. Maximum: 29. , 0 31. ,
33. (a) 25; two (b) , 1 35. (a) 0; one (b)
37. (a) ; none (b) No real solution
39. (a)
(b)
y = 2.4765x
2
- 8.827x + 9.7847
- 16
1
2
- 4
1
2
- 3- 7f A
3
2
B=
45
4
f A-
3
2
B=
7
4
f 1- 22=-11
y = 2x
2
- 8x + 5y =-
3
4
1x + 22
2
+ 6
y
x
1
0
1
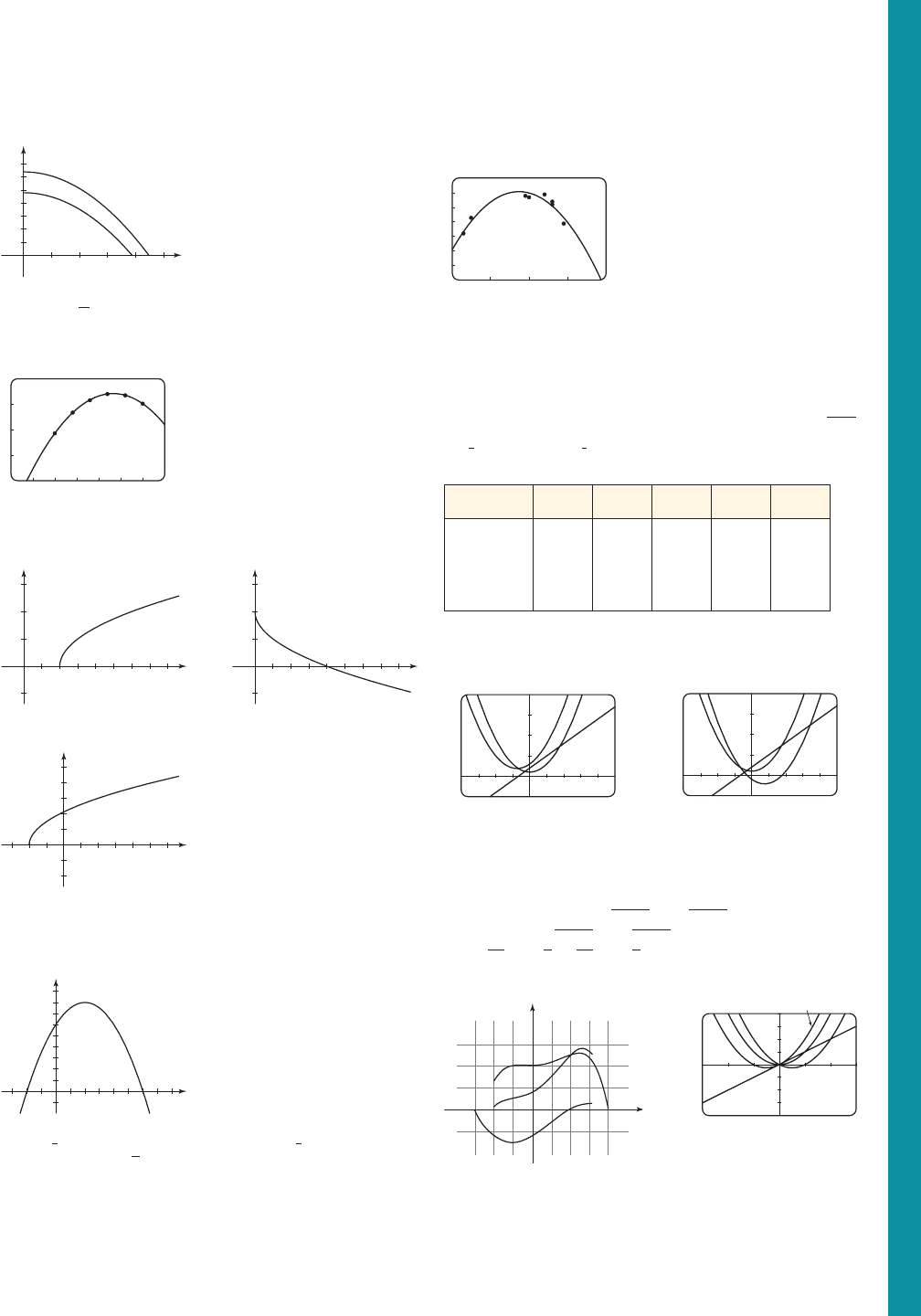
Answers to Section 6.1 A33
45. 47. (a) (b) 8 in. by 11 in.
49. (a)
(b) (c) 4.65 g
f 1x 2=-1.1021x
2
+ 10.249x - 1.7219
A1x 2= x1x + 3 2f 1x 2=
3
32
x
2
0
50
100
150
200
250
300
350
12345
y
x
h
1
h
2
25
5
7
0
y
0x
1
1
43. (a) (b) is a shift of
upward 80 units.
h
1
h
2
Chapter 5 Test
■
page 472
1. (a) (b)
(c)
2. (a)
(b) (2, 16) (c) , 6
(d) (e) Maximum: 16
- 2
f 1x 2=-1x - 22
2
+ 16
3. 4. (a) 49; two; ,
(b) 8; two; (c) ; none- 73 ; 22
1
3
- 2y =
1
2
1x - 42
2
- 6
y
0x
1
1
y
0x
1
2
y
0x
1
2
7
4
0
5. (a)
(b)
y =-1.3254x
2
+ 4.598x + 2.0934
Chapter 6
6.1 Exercises
■
page 489
1. (a) , ; 12, (b) , ;
18, 2. 8, , 15, 3. True 4. False
5.
3
5
- 2
1
2
f 1x 2
g1x 2
f 1x 2
#
g1x 2- 2f 1x 2- g1x 2f 1x 2+ g1x 2
20
_5
f+g
5
_4
f
g
20
_5
f-g
5
_4
f
g
t 0 1 2 3 4
f 1t 2
30 24 22 17 13
g1t 2
294 312 331 352 370
1f + g21t 2
324 336 353 369 383
1f - g21t 2 - 264
- 288 - 309 - 335 - 357
7. 3 9. 11. 0 13. (a)
(b) 1f - g21x2= 2x
2
- 3x - 1
1f + g21x 2= 2x
2
+ 3x + 3- 4
15. (a) , ;
, (b) ; 3
17. (a) , ;
, (b) ; 20
19. (a) , ;
,
(b) ;
21. 23.
110
- 16110 + 16
3- 3, q 21f - g21x2= 17 + x - 13 + x
3- 3, q 21f + g21x2= 17 + x + 13 + x
- 321- q, q 21f - g21x2= 8x
2
- 5x - 2
1- q, q 21f + g21x2=-6x
2
- 5x + 2
- 11- q, q 21f - g21x 2= x
2
- x + 3
1- q, q 21f + g21x 2= x
2
+ x - 3
y
x
0
g
f+g
f
4
_4
f
g
3
_3
f-gf+g
6. (a) 2500 ft (b) 1000 ft
