Stewart J. College Algebra: Concepts and Contexts
Подождите немного. Документ загружается.

T14 ALGEBRA TOOLKIT A
■
Working with Numbers
49–52
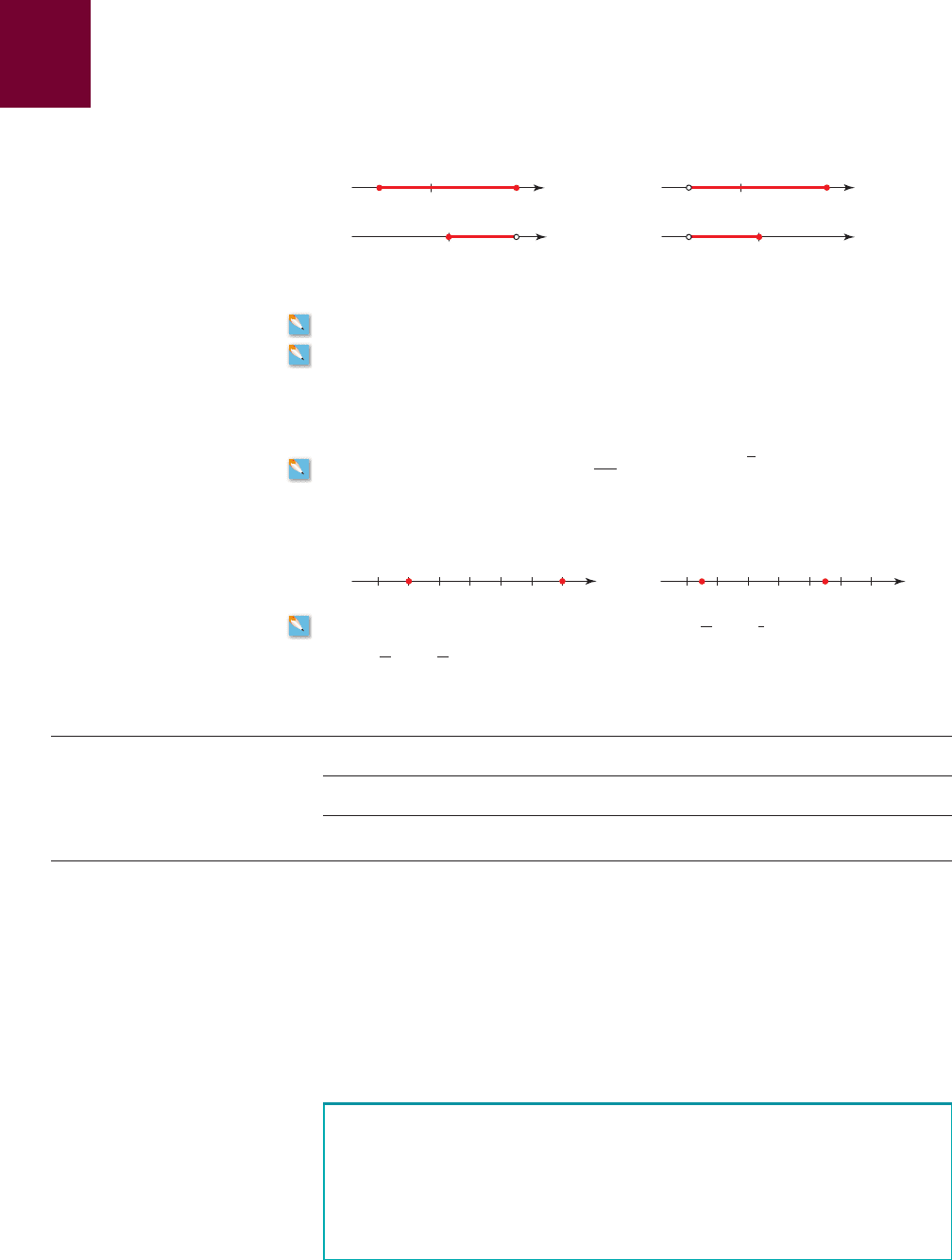
■ The graph of an interval is given. Express the interval (a) in set-builder notation
and (b) in interval notation.
49. 50.
51. 52.
53–58
■ Graph the set.
53. 54.
55. 56.
57. 58.
59–60
■ Evaluate each expression.
59. (a) (b) (c) (d)
60. (a) (b) (c) (d)
61–64
■ Find the distance between the given numbers.
61. 62.
63. (a) 2 and 17 (b) (c)
64. (a) (b) (c) - 2.6 and - 1.8- 38 and - 57
7
15
and -
1
21
11
8
and -
3
8
- 3 and 21
0
10 - p 00 1- 22
#
6 00 - 5 00 100 0
0
25 - 5 02
- 6
24
20 - 12 00 9 0
1- q, 6 2傽 12, 1021- q, - 42´ 14, q 2
3- 4, 62´ 30, 823- 4, 64傽 30, 82
1- 2, 02傽 1- 1, 121- 2, 02´ 1- 1, 12
5− 3 0
5_3 0
20
_2 0
321_3 _2 _1 0 321_3 _2 _1 0
2
A.3 Integer Exponents
2
■ Integer Exponents
A product of identical numbers is usually written in exponential notation. For example,
4 factors
We say that 9 is the base and 4 is the exponent. In general, we have the following
definition.
Exponential Notation
9
4
= 9 * 9 * 9 * 9
■
Integer Exponents
■
Rules for Working with Exponents
If a is any real number and n is a positive integer, then the nth power of a is
n factors
The number a is called the base and n is called the exponent.
a
n
= a * a *
p
* a
u
u

A.3
■
Integer Exponents T15
Let’s calculate some numbers written in exponential notation.
example
1
Using Exponential Notation
u
t
t
t
t
r
If a is any nonzero real number and n is a positive integer, then
a
0
= 1anda
-n
=
1
a
n
Let’s calculate some numbers with zero or negative exponents.
Evaluate each expression.
(a)
(b) (c) (d)
Solution
Using the definition of exponential notation, we can write out each number as follows.
(a)
(b)
(c)
(d)
■ NOW TRY EXERCISES 7 AND 9 ■
In Example 1, note the difference between and . In the expo-
nent applies to , but in the exponent applies only to 3.
We can state several useful rules for working with exponential notation. To dis-
cover the rule for multiplication, we multiply by :
4 factors 2 factors 6 factors
It appears that to multiply two powers of the same base, we add their exponents. In
general, for any real number a and any positive integers m and n, we have
m factors n factors m⫹n factors
We would like this rule to be true even when m and n are 0 or negative integers. For
instance, we must have
But this can happen only if . Likewise, we want to have
and this can be true only if . These observations lead to the following
definition.
Zero and Negative Exponents
5
-3
=
1
5
3
5
3
#
5
-3
= 5
3 +1-32
= 5
0
= 1
5
0
= 1
5
0
#
5
3
= 5
0 +3
= 5
3
a
m
#
a
n
= 1a
#
a
p
a21a
#
a
p
a2= 1a
#
a
p
a2= a
m +n
5
4
#
5
2
= 15
#
5
#
5
#
5215
#
52= 15
#
5
#
5
#
5
#
5
#
52= 5
6
= 5
2 +4
5
2
5
4
- 3
4
- 3
1- 32
4
- 3
4
1- 32
4
A
1
2
B
5
=
1
2
*
1
2
*
1
2
*
1
2
*
1
2
=
1
32
- 3
4
=-13
#
3
#
3
#
32=-81
1- 32
4
= 1- 321- 3 21- 321- 32= 81
10
6
= 10
#
10
#
10
#
10
#
10
#
10 = 1,000,000
A
1
2
B
5
- 3
4
1- 32
4
10
6
T16 ALGEBRA TOOLKIT A
■
Working with Numbers
example
2
Zero and Negative Exponents
Evaluate the following expressions.
(a) (b) (c) (d)
Solution
Using the definition of zero and negative exponents, we get the following.
(a)
(b)
(c)
(d)
■ NOW TRY EXERCISES 13 AND 15 ■
1- 42
-3
=
1
1- 42
3
=
1
1- 42
#
1- 42
#
1- 42
=
1
- 64
5
-1
=
1
5
1
=
1
5
5
-4
=
1
5
4
=
1
5
#
5
#
5
#
5
=
1
625
a
1
2
b
0
= 1
1- 42
-3
5
-1
5
-4
a
1
2
b
0
2
■ Rules for Working with Exponents
The following rules help us to simplify expressions that involve exponents. In the
table, the bases a and b are real numbers, and the exponents m and n are integers.
Rules for Working with Exponents
example
3
Working with Exponents
Use the rules of exponents to write each of the following expressions in as simple a
form as possible.
(a) (b) (c) (d) a
2
3
b
4
3
6
#
3
-2
3
7
5
7
3
110
3
2
2
If a and b are any nonzero real numbers and m and n are positive integers, then
Rule Verbal description
1. To multiply two powers of the same number, add the
exponents.
2. To divide two powers of the same number, subtract the
exponents.
3. To raise a power to another power, multiply the exponents.
4. To raise a product to a power, raise each factor to the
power.
5. To raise a quotient to a power, raise both numerator and
denominator to the power.
a
a
b
b
n
=
a
n
b
n
1ab 2
n
= a
n
b
n
1a
m
2
n
= a
mn
a
m
a
n
= a
m -n
a
m
a
n
= a
m +n
A.3
■
Integer Exponents T17
Solution
Using the rules of exponents, we can simplify these expressions as follows.
(a) Using Rule 3, we have
(b) Using Rule 2, we have
(c) Using Rules 1 and 2, we have
(d) Using Rule 5, we have
■ NOW TRY EXERCISES 19, 25, 29, AND 31 ■
a
2
3
b
4
=
2
4
3
4
=
16
81
3
6
#
3
-2
3
=
3
6 +1-22
3
= 3
6 +1-22- 1
= 3
3
= 27
7
5
7
3
= 7
5 -3
= 7
2
= 49
110
3
2
2
= 10
3
#
2
= 10
6
= 1,000,000
example
4
Working with Exponents
Each of the following expressions contains one or more variables. We use the rules
of exponents to simplify each expression.
(a) (b) (c) (d)
Solution
(a) Using Rule 1, we have
(b) Using Rules 3 and 4, we have
(c) Using Rule 4, we have
(d) Using Rules 3 and 5, we have
■ NOW TRY EXERCISES 35, 37, 41, AND 51 ■
The rules of exponents can be used in different ways. Sometimes one way in-
volves fewer steps than another, even though the final simplification is the same, as
we see in the next example. So as long as you use the rules correctly, you may apply
them in any order you like.
a
a
2
2b
b
4
=
a
2
#
4
2
4
b
4
=
a
8
16b
4
1- 2x2
5
= 1- 22
5
x
5
=-32x
5
1xy
2
2
3
= x
3
y
2
#
3
= x
3
y
6
x
5
x
2
= x
5 +2
= x
7
a
a
2
2b
b
4
1- 2x2
5
1xy
2
2
3
x
5
x
2
T18 ALGEBRA TOOLKIT A
■
Working with Numbers
example
5
Using the Rules of Exponents in Different Ways
Show two different ways to simplify the expression .
Solution 1
Here’s one way: We start with Rule 5.
Rule 5
Rules 3 and 4
Simplify
Rule 2
Simplify
Solution 2
Here’s another way that starts with Rule 2.
Rule 2
Simplify
Rule 5
Simplify
■ NOW TRY EXERCISE 47 ■
=
x
2
25
=
x
2
5
2
= a
x
5
b
2
a
x
4
5x
3
b
2
= a
x
4 -3
5
b
2
=
x
2
25
=
x
8 -6
25
=
x
8
25x
6
=
x
4
#
2
5
2
x
3
#
2
a
x
4
5x
3
b
2
=
1x
4
2
2
15x
3
2
2
a
x
4
5x
3
b
2
A.3 Exercises
CONCEPTS
1. Using exponential notation, we can write the product as _______.
2. In the expression the number 3 is called the
_______ and the number 4 is called the
______________.
3. When we multiply two powers with the same base, we
_______ the exponents. So
_______.
4. When we divide two powers with the same base, we
_______ the exponents. So
_______.
3
5
3
2
=
3
4
#
3
5
=
3
4
5
#
5
#
5
#
5
#
5
#
5

A.3
■
Integer Exponents T19
5. When we raise a power, to a new power, we _______ the exponents.
So
_______.
6. Express the following numbers without using exponents.
(a)
_______.
(b)
_______.
(c)
_______.
7–16
■ Evaluate each expression.
7. (a) (b) 8. (a) (b)
9. (a) (b) 10. (a) (b)
11. (a) (b) 12. (a) (b)
13. (a) (b) 14. (a) (b)
15. (a) (b) 16. (a) (b)
17–34
■ Use the rules of exponents to write each expression in as simple a form as
possible.
17. 18.
19. 20.
21. 22.
23. 24.
25. 26.
27. 28.
29. 30.
31. 32.
33. 34.
35–52
■ Simplify each expression, and eliminate any negative exponents.
35. 36.
37. 38.
39. 40.
41. 42.
43. 44.
45. 46.
47. 48.
49. 50.
51. 52. a
- 2x
2
y
3
b
3
a
3u
5
2√
3
b
4
12z
2
2
-5
z
10
13z2
2
16z
2
2
-3
3x
4
4x
2
a
a
2
4a
3
b
3
z
2
z
4
z
3
z
-1
a
9
a
-2
a
x
6
x
10
y
10
y
0
y
7
1- 2w2
4
1- 3a2
3
12a
3
a
2
2
4
1a
2
a
4
2
3
18x 2
2
12y
2
2
3
x
2
x
-6
x
8
x
2
A
5
3
B
0˛
2
-1
A
1
2
B
4
A
5
2
B
-2
A
2
3
B
-3
A
3
4
B
2
2
-3
#
2
2
3
0
7
5
#
7
-3
7
2
5
4
#
5
-2
3
-4
#
3
2
3
3
-2
10
7
10
4
1- 32
2
- 3
2
- 6
0
1- 62
0
12
3
2
0
12
3
2
2
2
3
#
2
2
5
2
#
5
10
-6
10
-1
3
-3
3
-1
1- 22
0
2
0
- 3
0
A
1
3
B
0
- 3
7
1- 32
7
- 6
3
1- 62
3
- 10
4
1- 102
4
- 5
2
1- 52
2
A
1
2
B
4
2
6
A
1
3
B
5
3
4
A
1
2
B
-1
=
2
-3
=
2
-1
=
13
4
2
2
=
SKILLS
T20 ALGEBRA TOOLKIT A
■
Working with Numbers
2
A.4 Radicals and Rational Exponents
2
■ Rational Exponents: a
1>n
■
Rational Exponents:
■
Rational Exponents: a
m>n
a
1>n
To define what is meant by a rational exponent such as , we need to use radicals.
We want to give a meaning to the symbol in a way that is consistent with the
rules of exponents. To do this, we notice that when we square , we get a because
Since squared is a, it follows that
Similarly, , so must be the nth root of a.
Exponential Notation for 1
n
a
a
1>n
1a
1>n
2
n
= a
a
1>2
= 1a
a
1>2
1a
1>2
2
2
= a
2
#
11>22
= a
1
= a
a
1>2
a
1>2
a
1>2
It is true that positive numbers have two square roots; for example, the number 9
has the two square roots 3 and , but the notation is reserved for the positive
square root (called the principal square root). If we want the negative square root,
we must write , which is .
If n is an even integer, then a must be nonnegative for to be defined. This is
because we can’t take the square root (or fourth root, sixth root, etc.) of negative
numbers. Here are some examples of numbers with rational exponents.
a
1>n
- 3- 29
29- 3
If n is a positive integer, then we define
When n is even, we require that .a Ú 0
a
1>n
= 1
n
a
example
1
Rational Exponents
Evaluate.
(a) (b) (c) (d)
Solution
(a) Because
(b) Because
(c) Because
(d) Because
■ NOW TRY EXERCISE 19 ■
a
2
3
b
4
=
16
81
a
16
81
b
1>4
=
2
3
a
1
2
b
3
=
1
8
a
1
8
b
1>3
=
1
2
1- 52
3
=-1251- 125 2
1>3
=-5
3
2
= 99
1>2
= 3
a
16
81
b
1>4
a
1
8
b
1>3
1- 1252
1>3
9
1>2

A.4
■
Radicals and Rational Exponents T21
If m and n are positive integers, then we define
or equivalently
When n is even, we require that .a Ú 0
a
m>n
= 1
n
a
m
a
m>n
= A1
n
a B
m
2
■ Rational Exponents: a
m>n
To define the meaning of a rational exponent such as , we simply notice that the
rules of exponents tell us that or, equivalently, . We can
compute each of these expressions:
In either case we get the same value 4 for . The same reasoning allows us to give
the appropriate meaning for . For any rational exponent in lowest terms, where
m and n are integers and , we have the following definition.
Exponential Notation for 2
n
a
m
n 7 0
m
n
a
m>n
8
2>3
8
2>3
= 18
2
2
1>3
= 64
1>3
= 4
8
2>3
= 18
1>3
2
2
= 2
2
= 4
8
2>3
= 18
2
2
1>3
8
2>3
= 18
1>3
2
2
8
2>3
If n is an even integer, then a must be nonnegative for to be defined. Note
that the rules of exponents also hold for rational exponents. Here are some examples
of numbers involving rational exponents.
a
m>n
example
2
Rational Exponents
Calculate.
(a) (b) (c) (d)
Solution
(a) Rule 3:
Because
Calculate
(b) Rule 3:
Because
Because
(c) Rule 3:
Because
Property of Negative Exponents
Calculate
= 8
= 2
3
2
5
1>32 = 1>2 = a
1
2
b
-3
1a
m
2
n
= a
mn
a
1
32
b
-3>5
= aa
1
32
b
1>5
b
-3
2
3
64 = 4 = 4
1- 82
2
= 64 = 64
1>3
1a
m
2
n
= a
mn
1- 82
2>3
= 11- 82
2
2
1>3
= 8
2
4
16 = 2 = 2
3
1a
m
2
n
= a
mn
16
3>4
= 116
1>4
2
3
a
8
27
b
4>3
a
1
32
b
-3>5
1- 82
2>3
16
3>4

example
4
Simplifying by Writing Radicals as Rational Exponents
Simplify.
(a)
(b) 2
x1x
12 1x2131
3
x2
T22 ALGEBRA TOOLKIT A
■
Working with Numbers
(d) Rule 3:
Because
Rule 5:
■ NOW TRY EXERCISE 21 ■
a
a
b
b
n
=
a
n
b
n
=
16
81
2
3
8 = 2 and 2
3
27 = 3 = a
2
3
b
4
1a
m
2
n
= a
mn
a
8
27
b
4>3
= aa
8
27
b
1>3
b
4
example
3
Using the Laws of Exponents with Rational Exponents
Simplify the expression and eliminate any negative exponent(s). Assume that all let-
ters denote positive numbers.
(a)
(b)
(c)
Solution
(a) Rule 1:
Simplify
(b) Rule 2:
Simplify
Definition of negative exponents
(c) Rule 4:
Rule 3:
Simplify
■ NOW TRY EXERCISES 23, 27, AND 31 ■
= 8a
9>2
b
6
1a
m
2
n
= a
mn
= 12
3
2a
313>22
b
413>22
1abc 2
n
= a
n
b
n
c
n
14a
3
b
4
2
3>2
= 4
3>2
1a
3
2
3>2
1b
4
2
3>2
=
1
a
1>5
= a
-1>5
a
m
a
n
= a
m - n
a
2>5
a
3>5
= a
2>5 -3>5
= a
8>3
a
m
a
n
= a
m + n
a
1>3
a
7>3
= a
1>3 +7>3
14a
3
b
4
2
3>2
a
2>5
a
3>5
a
1>3
a
7>3

A.4 Exercises
CONCEPTS
1. Using exponential notation, we can write as _______.
2. Using radicals, we can write as
_______.
3. Is there a difference between and ? Explain.
4. Explain what means, and then calculate in two different ways:
5. Find the missing power in the following calculation:
6. Find the missing power in the following calculation:
7–14
■ Write each radical expression using exponents and each exponential expression
using radicals.
Radical Exponential
expression expression
7. _______
8. _______
9. _______
10. _______
11. _______
12. _______
13. _______
14. _______
1
2x
5
a
2>5
2
-1>2
2
5
5
3
11
-3>2
4
2>3
2
3
7
2
1
25
5
1>3
#
5
= 1
5
1>3
#
5
= 5
4
3>2
= 14
3
2
= _________4
3>2
= 14
1>2
2
= _________
4
3>2
4
3>2
1252
2
25
2
5
1>2
2
3
5
SKILLS
A.4
■
Radicals and Rational Exponents T23
Solution
(a) Definition of rational exponents
Rule 1:
Simplify
(b) Definition of rational exponents
Rule 1:
Rule 3:
■ NOW TRY EXERCISES 41 AND 47 ■
1a
m
2
n
= a
mn
= x
3>4
a
m
a
n
= a
m + n
= 1x
3>2
2
1>2
2
x1x = 1x
#
x
1>2
2
1>2
= 6x
5>6
a
m
a
n
= a
m + n
= 6
1>2 +1>3
121x2131
3
x2= 12x
1>2
213x
1>3
2
