Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

T4 ALGEBRA TOOLKIT A

■

Working with Numbers

example

Using the Distributive Property to Expand

Expand the products using the Distributive Property.

(a)

(b)

(c)

Solution

(a) We use the Distributive Property.

Distributive Property

Simplify

(b) The minus sign is the same as multiplying by .

Distributive Property

Simplify

Notice how the negative sign outside the parentheses switches the signs of the

terms inside the parentheses.

Distributive Property

Simplify

■ NOW TRY EXERCISES 27, 31, AND 33 ■

= 7x

+ 14xy + 28x

7 x˛ 1x + 2y + 4 2= 7x

x + 7x

2y + 7x

=-2 + x

= 1- 122 + 1- 121- x2

- 12 - x 2=-112 - x 2

- 1

= ax + 5ay

a1x + 5y 2= a

x + a

7x˛ 1x + 2y + 4 2

- 12 - x2

a1x + 5y2

EXPANDING

The expression inside the

parentheses in Example 3(c) has

three terms.

x + 2y + 4

x˛ 13 + 2y 2= x

3 + x

2y = 3x + 2xy

So for any numbers x and y it is true that . For instance, we

can check that this is true when x is 5 and y is 8:

Right-hand side: 3

5 + 2

8 = 15 + 80 = 95

Left-hand side: 513 + 2

82= 5119 2= 95

x13 + 2y 2= 3˛x + 2xy

Three terms

■ The Distributive Property: Factoring

Factoring is the reverse of expanding. When we factor, we use the Distributive

Property to write an expression as a product of simpler ones.

513 + x 2= 15 + 5x

EXPANDING

FACTORING

A.1

■

Numbers and Their Properties T5

example

Using the Distributive Property to Factor

Factor the following using the Distributive Property.

(a)

(b)

(c)

(d)

Solution

(a) The common factor in each term is 3. So we factor 3 from each term using the

Distributive Property.

Distributive Property

(b) The common factor in each term is a. So we factor a from each term using the

Distributive Property.

Distributive Property

using the Distributive Property.

Distributive Property

(d) The expression 3b is common to each term. So we factor 3b from each term

using the Distributive Property (applied to the three terms).

Distributive Property

■ NOW TRY EXERCISES 35, 39, AND 43 ■

3abc + 6ab + 3bc = 3b1ac + 2a + c2

2bx + 4x = 2x1b + 22

ax + 2ay = a1x + 2y2

3x + 3

1 = 31x + 12

3abc + 6ab + 3bc

2bx + 4x

ax + 2ay

3x + 3

In Example 4(b), a is a common

factor of the terms ax and ay.

3abc + 6ab + 3bc

ax + 2ay

To use the Distributive Property in reverse, we look for common factors of each of

the terms in the expression we are factoring.

a is a factor

of each term

3b is a factor

of each term

A.1 Exercises

CONCEPTS

1. Give an example of each of the following:

(a) A natural number

(b) An integer that is not a natural number

(d) An irrational number

2. Complete each statement and name the property of real numbers you used.

(a) ________________; ________________ Property

(b) ________________; ________________ Property

3. (a) When two numbers are multiplied together, each of the numbers is called a

________________ (term/factor). So in the product 3xy the numbers 3, x, and y are

________________.

a1b + c2=

a + 1b + c 2=

ab =

T6 ALGEBRA TOOLKIT A

■

Working with Numbers

SKILLS

(b) When two numbers are added together, each of the numbers is a

_____________ (term/factor). So in the sum the expressions 3 and xy

are

_____________.

4. (a) We use the

_____________ _____________ to expand expressions, so to

expand the expression , we multiply each term inside the parentheses by

_______, and get _______ _______.

(b) We use the

_____________ _____________ to factor. The expression

has a common factor

_______, so to factor the expression , we

factor

_______ from each term and get ______________.

5–6

■ List the elements of the given set that are:

(a) Natural numbers

(b) Integers

(d) Irrational numbers

7–10

■ Evaluate the arithmetic expression.

7. 8.

9. 10.

11–18

■ State the property of real numbers being used.

11. 12.

13. 14.

15. 16.

17. 18.

19–22

■ Evaluate the given expression.

19. 20. 21. 22.

23–26

■ Evaluate the given expression directly, then evaluate using the Distributive

Property.

23. 24.

25. 26.

27–34

■ Expand the expression using the Distributive Property.

27. 28.

29. 30.

31. 32.

33. 34. 13q - 2qr - 5r 21- 2ps24mn12p + 3pq - 2q2

- 3c16ab - 5bd2- 413ax - 2x 2

1x + 2y 271a - 3c 26

81a - 2231x + 72

- 0.3130 - 202113 - 1021- 102

120 + 142

53110 + 22

6 - 16

2 - 7

10 - 4

5 - 2

4 - 9

10 - 4

71a + b + c2= 71a + b2+ 7c2x13 + y2= 13 + y22x

1x + a 21x + b 2= 1x + a2x + 1x + a2b15x + 123 = 15x + 3

21A + B2= 2A + 2B1x + 2y2+ 3z = x + 12y + 3z2

13 + 52= 13 + 5227 + 10 = 10 + 7

1 - 23 3 - 415 - 6

724

5 + 7

- 6312 - 117 - 2

324

314

6 - 2

102+ 7115 - 8

22- 2 + 34

7 - 5A9 -

51.001, 0.3

, - p, - 11, 11,

, 3.14, 116,

50, - 10, 50,

, 0.583, 17, 1.23, -

ab + ac =

ab + acab + ac

+a1b + c2=

a1b + c2

3 + xy

_3_4 _2 _1 0 1 2 3 4

_3_π œ∑ 22

figure 2

A.2

■

The Number Line and Intervals T7

35–42 ■ Factor the given expression using the Distributive Property.

35. 36.

37. 38.

39. 40.

41. 42.

43. 44.

abx +

aby -

abz2qrs - 6qst + 12rst

- 30xz - 90yz- 5ab + 10bc

2ax + 2ayab - 6b

- 20x + 40y- 2a - 2b

6y - 123x + 9

A.2 The Number Line and Intervals

■ The Real Line

The real numbers can be represented by points on a line, as shown in Figure 1. The

positive direction (toward the right) is indicated by an arrow. We choose an arbitrary

reference point O, called the origin, which corresponds to the real number 0. Given

any convenient unit of measurement, each positive number x is represented by the

point on the line a distance of x units to the right of the origin, and each negative num-

ber is represented by the point x units to the left of the origin. Thus every real

number is represented by a point on the line, and every point P on the line corre-

sponds to exactly one real number.

The number associated with the point P is called the coordinate of P, and the

line is then called a coordinate line, or a real number line, or simply a real line.

Often we identify the point with its coordinate and think of a number as being a point

on the real line.

- x

■

The Real Line

■

Order on the Real Line

■

Sets and Intervals

■

Absolute Value and Distance

_3 _2 _1 0 1 2 3 4

_2.2

0.1 3.9

figure 1 The real line

■ Order on the Real Line

The real numbers are ordered. We say that a is less than b and write if is

a positive number. Geometrically, this means that a lies to the left of b on the number

line. (Equivalently, we can say that b is greater than a and write .) The symbol

(or ) means that either or and is read “a is less than or equal

to b.” For instance, the following are true inequalities (see Figure 2):

- p 6-312 6 22 … 2

a = ba 6 bb Ú aa … b

b 7 a

b - aa 6 b

T8 ALGEBRA TOOLKIT A

■

Working with Numbers

example

Graphing Inequalities

(a) On the real line, graph all the numbers x that satisfy the inequality .

(b) On the real line, graph all the numbers x that satisfy the inequality .

Solution

(a) We must graph the real numbers that are smaller than 3: those that lie to the

left of 3 on the real line. The graph is shown in Figure 3. Note that the number

3 is indicated with an open dot on the real line, since it does not satisfy the

inequality.

(b) We must graph the real numbers that are greater than or equal to : those

that lie to the right of on the real line, including the number itself. The

graph is shown in Figure 4. Note that the number is indicated with a solid

dot on the real line, since it satisfies the inequality.

■ NOW TRY EXERCISES 17 AND 19 ■

- 2

- 2- 2

- 2

x Ú-2

x 6 3

figure 4

figure 3

■ Sets and Intervals

A set is a collection of objects, and these objects are called the elements of the set.

Some sets can be described by listing their elements within braces. For instance, the

set A that consists of all positive integers less than 7 can be written as

We could also write A in set-builder notation as

which is read “A is the set of all x such that x is an integer and .”

If S and T are sets, then their union is the set that consists of all ele-

ments that are in S or T (or in both). The intersection of S and T is the set

consisting of all elements that are in both S and T. In other words, is the

common part of S and T. The empty set, denoted by , is the set that contains no

element.

⭋

S 傽 T

S ´ T

0 6 x 6 7

A = 5x

0 x is an integer and 0 6 x 6 76

A = 51, 2, 3, 4, 5, 66

example

Union and Intersection of Sets

If , , and , find the sets , ,

and .

Solution

All elements in S or T

Elements common to both S and T

S and have no elements in common

■ NOW TRY EXERCISE 31 ■

V S 傽 V = ⭋

S 傽 T = 54, 56

S ´ T = 51, 2, 3, 4, 5, 6, 76

S 傽 V

S 傽 TS ´ TV = 56, 7, 86T = 54, 5, 6, 76S = 51, 2, 3, 4, 56

A.2

■

The Number Line and Intervals T9

Certain sets of real numbers, called intervals, occur frequently in algebra and

correspond geometrically to line segments. For example, if , then the open in-

terval from a to b consists of all numbers between a and b, excluding the endpoints

a and b. The closed interval includes the endpoints. We can write these intervals in

set-builder notation:

Open interval Closed interval

When we graph these intervals on the real line, we use a solid dot to indicate that an

endpoint is included and an open circle to indicate that an endpoint is excluded. The

graphs are shown below.

3a, b4= 5x

0 a … x … b61a, b 2= 5x 0 a 6 x 6 b6

a 6 b

We also need to consider infinite intervals. For example, all the numbers greater

than 3 form the interval . This does not mean that (“infinity”) is a number.

The notation stands for the set of all numbers that are greater than a, so the

symbol simply indicates that the interval extends indefinitely far in the positive di-

rection. Similarly, is the interval consisting of all numbers less than or equal

to 3 (the bracket on the right-hand side of the interval indicates that we include 3).

We graph these intervals on the real line.

1- q, 34= 5x 0 x … 3613, q 2= 5x 0 3 6 x6

1- q, 34

1a, q 2

q13, q 2

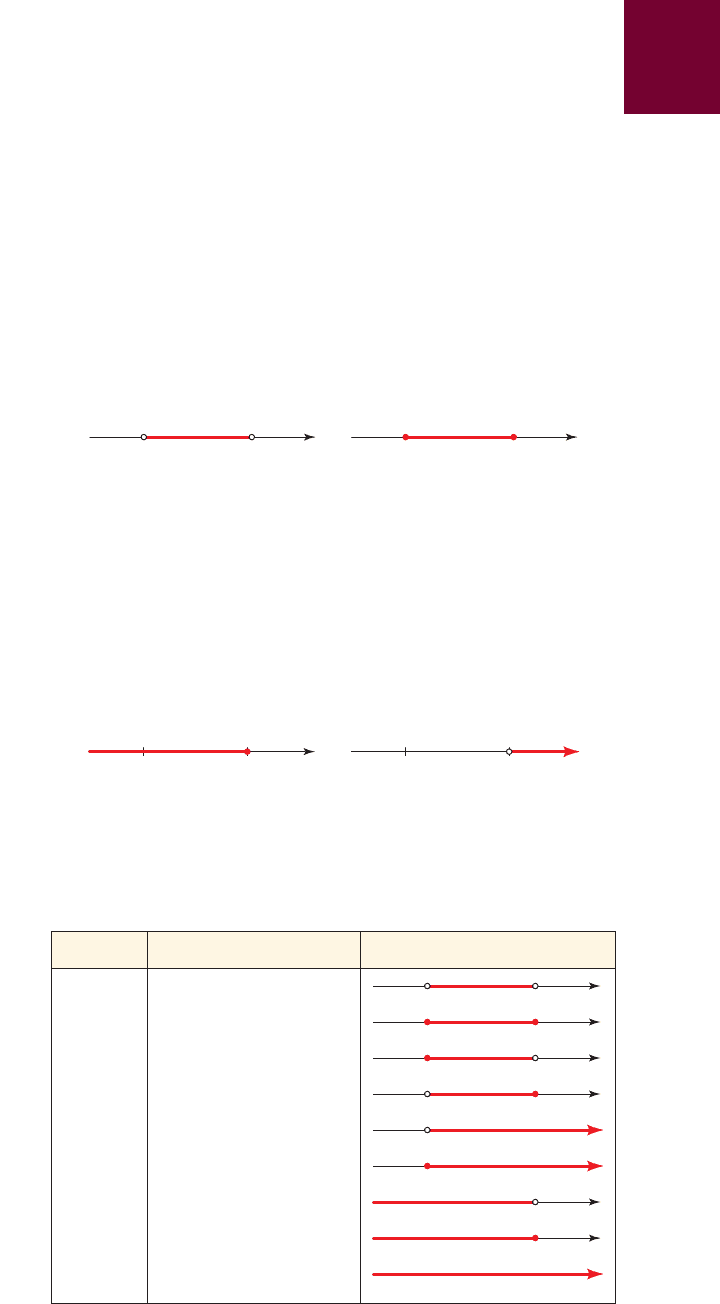
Table 1 lists the nine possible types of intervals. When these intervals are dis-

cussed, we will always assume that .a 6 b

Notation Set description Graph

1a, b 2 5x 0 a 6 x 6 b6

3a, b4 5x 0 a … x … b6

3a, b2 5x 0 a … x 6 b6

1a, b 4 5x 0 a 6 x … b6

1a, q 2 5x 0 a 6 x6

3a, q 2 5x 0 a … x6

1- q, b 2 5x 0 x 6 b6

1- q, b 4 5x 0 x … b6

1- q, q 2 (set of all real numbers)⺢

table 1

T10 ALGEBRA TOOLKIT A

■

Working with Numbers

example

Verbal Description of an Interval

Consider the interval .

(a) Give a verbal description of the interval.

(b) Express the interval in set builder notation.

Solution

(a) The interval consists of all numbers between 2 and 5, including 5 but

excluding 2.

(b)

12, 5 4= 5x 0 2 6 x … 56

12, 5 4

example

Graphing Intervals

■ NOW TRY EXERCISES 35 AND 37 ■

_1 20

1.5 4

■ NOW TRY EXERCISE 33 ■

example

Finding Unions and Intersections of Intervals

Graph each set.

(a) (b)

Solution

(a) The intersection of two intervals consists of the numbers that are in both

intervals. Therefore,

This set is illustrated in Figure 5.

(b) The union of two intervals consists of the numbers that are in either one

interval or the other (or both). Therefore,

= 5x

0 2 … x 6 36= 32, 3 2

11, 32傽 32, 74= 5x 0 1 6 x 6 3 and 2 … x … 76

11, 32´ 32, 7411, 32傽 32, 74

Express each interval in set builder notation, and then graph the interval.

(a) (b) (c)

Solution

(a)

(b)

0 - 3 6 x6

31.5, 44= 5x 0 1.5 … x … 46

3- 1, 22= 5x 0 - 1 … x 6 26

1- 3, q 231.5, 443- 1, 22

A.2

■

The Number Line and Intervals T11

This set is illustrated in Figure 6.

= 5x 0 1 6 x … 76= 11, 74

11, 32´ 32, 7 4= 5x 0 1 6 x 6 3 or 2 … x … 76

(1, 3)

[2, 7]

[2, 3)

figure 5

11, 3 2傽 32, 74

(1, 3)

[2, 7]

(1, 7]

figure 6 11, 32´ 32, 74

■ Absolute Value and Distance

The absolute value of a number a, denoted by , is the distance from a to 0 on the

real number line (see Figure 7). Distance is always positive or zero, so we have

for every number a. Remembering that is positive when a is negative,

we have the following definition.

Absolute Value

- a0 a 0Ú 0

0 a 0

If a is a real number, then the absolute value of a is

a 0= e

aif a Ú 0

- aif a 6 0

50_3

|5|=5|_3|=3

figure 7

example

Evaluating Absolute Values of Numbers

Evaluate.

(a) (b) (c) (d)

Solution

(a)

(b)

(c)

(d)

■ NOW TRY EXERCISE 59 ■

0 12 - 1 0 = 12 - 1 1because 12 7 1, and so 12 - 1 7 02

0 0 0= 0

0 - 3 0=-1- 32= 3

0 3 0= 3

0 12 - 1 00 0 00 - 3 00 3 0

■ NOW TRY EXERCISES 53 AND 55 ■

T12 ALGEBRA TOOLKIT A

■

Working with Numbers

110_2

figure 8

|b-a|

figure 9 Length of a line segment

is 0

b - a 0

What is the distance on the real line between the numbers and 11? From

Figure 8 we see that the distance is 13. We arrive at this by finding either

or . From this observation we make the fol-

lowing definition (see Figure 9).

Distance Between Points on the Real Line

01- 22- 11 0= 13011 - 1- 2 20= 13

- 2

If a and b are real numbers, then the distance between the points a and b on

the real line is

d1a, b 2= 0

b - a 0

Note that . This confirms that, as we would expect, the dis-

tance from a to b is the same as the distance from b to a.

0 b - a 0= 0 a - b 0

example

Distance Between Points on the Real Line

The distance between the numbers and 2 is

We can check this calculation geometrically, as shown in Figure 10.

■ NOW TRY EXERCISE 63 ■

d1a, b 2= 0 - 8 - 2 0= 0 - 10 0= 10

- 8

20_8

figure 10

A.2 Exercises

CONCEPTS

1. Explain how to graph numbers on a real number line.

2. If , how are the points on a real line that correspond to the numbers a and b

related to each other?

3. The set of numbers between but not including 2 and 7 can be written as follows:

(a)

_____________ in set builder notation

(b)

_____________ in interval notation

4. Explain the differences between the following two sets: and

5. The symbol stands for the

_____________ of the number x. If x is not 0, then

the sign of is always

_____________.

6. The absolute value of the difference between a and b is (geometrically) the

_____________ between them on the real line.

7–8

■ Place the correct symbol in the space.

7. (a) (b) (c)

8. (a) (b) (c)

9–16 ■ State whether each inequality is true or false.

9. 10. 11. 12.

13. 14. 15. 16. 8 … 81.1 7 1.1

8 … 9- p 7-3

6-1

12 7 1.41- 6 6-10

0.67 0

ⵧ

0- 0.67 0

ⵧ

- 0.67

ⵧ

0.67

3.5

ⵧ

- 3

ⵧ

16 , 7 , or = 2

x 0

B = 1- 2, 52A = 3- 2, 54

a 6 b

SKILLS

A.2

■

The Number Line and Intervals T13

17–20 ■ On a real line, graph the numbers that satisfy the inequality.

17. 18. 19. 20.

21–24

■ Find the inequality whose graph is given.

21. 22.

23. 24.

25–26

■ Write each statement in terms of inequalities.

25. (a) x is positive. (b) t is less than 4.

(e) The distance from p to 3 is at most 5.

26. (a) y is negative. (b) is greater than 1.

(e) y is at least 2 units away from 7.

27–30

■ Find the indicated set if , , and

27. (a) (b)

28. (a) (b)

29. (a) (b)

30. (a) (b)

31–32

■ Find the indicated set if , , and

31. (a) (b)

32. (a) (b)

33–40

■ Consider the given interval.

(a) Give a verbal description of the interval.

(b) Express the interval in set builder notation.

33. 34.

35. 36.

37. 38.

39. 40.

41–48

■ Express the inequality in interval notation, and then graph the corresponding

interval.

41. 42.

43. 44.

45. 46.

47. 48. - 5 … x 6-2x 7-1

x … 1x Ú-5

- 5 6 x 6 2- 2 6 x … 1

3 6 x 6 51 … x … 2

3- 3, q 21- q, - 22

1- q, 1 232, q 2

3- 6, -

432, 82

12, 8 41- 3, 02

A 傽 CA ´ C

B 傽 CB ´ C

C = 5x

0 - 1 6 x … 56

B = 5x

0 x 6 46A = 5x 0 x Ú-26

A 傽 B 傽 CA ´ B ´ C

A 傽 CA ´ C

B 傽 CB ´ C

A 傽 BA ´ B

C = 57, 8, 9, 106

B = 52, 4, 6, 86A = 51, 2, 3, 4, 5, 6, 76

- 5

- 1

x … 0x 6-3x 7-4x Ú 1