Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

2. Suppose Companies A and B share the losses equally; that is, each company

loses the same amount.

(a) Let x be the amount Company A receives and y be the amount Company B

receives when the $300 million are distributed. What is the net loss for

each company?

A’s net loss: __________ B’s net loss: __________

(b) To find x and y, we need to solve two equations. What does the fact that

the assets total $300 million tell us about x and y?

and y?

(d) Write the equation from parts (b) and (c) in the form .

(e) Find where the lines in part (d) meet. How much does each company

receive?

A gets: __________ B gets: __________

(f) One of the values in part (e) is negative. What does this mean? What

would the company getting the negative amount have to do?

(g) Do you think this is a fair method? Explain.

3. Suppose Companies A and B get the same fixed percentage of what they are

owed.

(a) Let x be the percentage of what they are owed. How much does each

company receive?

(b) The total amount to be distributed to Companies A and B is $300 million.

Use this fact together with the amounts in part (a) to write an equation

involving x.

(d) Use the percentage x to calculate how much each company receives.

A gets:



ⵧ

100

* _____ = _____B gets:

ⵧ

100

* _____ = _____

x  __________

__________  __________  300

A gets:

100

* ________B gets:

100

* _________

Second equation:y = ___________

First equation:y = ____________

y = b + mx

Second equation: ____________  ____________

First equation:x + y = _________

244 CHAPTER 2

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

■

EXPLORATIONS

EXPLORATIONS 245

(e) Do you think this is a fair method? Explain.

4. Suppose Companies A and B get an amount proportional to what they are owed.

(a) What is the total amount T owed to Companies A and B together?

(b) What proportion of the total claim T is owed to Company A?

To Company B?

the proportions in part (b).

(d) Do you think this is a fair method? Explain.

5. Notice that the amounts distributed to Companies A and B in Questions 3 and

4 are the same. Is this a coincidence, or are the methods really the same? Give

reasons for your answer.

6. Can you think of another fair way to divide the assets between Companies A

and B? Is your method fairer than the methods already described? Explain.

II. Profit Sharing

Anita and Karim pool their savings to start a business that imports wicker furni-

ture. Anita invests $2.6 million, and Karim invests $1.4 million. After three years

of successful operation, the business is sold to a national chain of furniture stores

for $6.4 million. How should Anita and Karim divide the $6.4 million? Here are

several possibilities:

■

They divide the $6.4 million equally.

■

Each gets their original investment back, and they share the profit equally.

■

Each gets a fraction of the $6.4 million proportional to the amount they

invested.

■

Each gets their original investment back plus a fraction of the profit propor-

tional to the amount they invested.

1. Investigate each of these methods to see which alternative is most fair.

2. You should have found that the last two methods result in Anita and Karim

receiving the same amount. Explain why the two methods are really the same.

3. How do you think partnerships like the one described here normally divide

their profits in the real world?

B gets:

______  300  _______

A gets:______  300  _______

B’s proportion:

ⵧ

= ____________

A’s proportion:

ⵧ

= ____________

T  ______  ______  ______

This page intentionally left blank

247

Population explosion? Cities and towns all over the world have

experienced huge increases in population over the past century. The above

photos of Hollywood in the 1920s and in 2000 tell the population story quite

dramatically. But to find out where population is really headed, we need a

mathematical model. Population grows in much the same way as money

grows in a bank account: The more money in the account, the more interest is

paid. In the same way, the more people there are in the world, the more babies

are born. This type of growth is modeled by exponential functions, the topic of

this chapter. According to some exponential models, world population will

double in successive 40-year periods, ending in a population explosion.

However, a different exponential model, which takes into account the limited

resources available for growth, predicts that world population will eventually

stabilize at a supportable level (see Exercise 33 on page 285).

3.1 Exponential Growth

and Decay

3.2 Exponential Models:

Comparing Rates

3.3 Comparing Linear

and Exponential Growth

3.4 Graphs of Exponential

Functions

3.5 Fitting Exponential Curves

to Data

EXPLORATIONS

Extreme Numbers:

Scientific Notation

2 So You Want to Be

a Millionaire?

3 Exponential Patterns

4 Modeling Radioactivity

with Coins and Dice

Exponential Functions

and Models

3.1 Exponential Growth and Decay

■

An Example of Exponential Growth

■

Modeling Exponential Growth: The Growth Factor

■

Modeling Exponential Growth: The Growth Rate

■

Modeling Exponential Decay

IN THIS SECTION… we find functions that model growth and decay processes (such as

population growth or radioactive decay). We use these models to predict future trends. The

functions we use are called exponential functions because the independent variable is in

the exponent.

GET READY… by reviewing the properties of exponents in Algebra Toolkits A.3 and

A.4. Test your understanding by doing the Algebra Checkpoint on page 255.

In Chapter 2 we studied linear functions, that is, functions that have constant

rates of change. We learned that linear functions can be used to model many real-

world situations. But there are important real-world phenomena in which the rate

of change is not constant. For example, the rate at which population grows is not

constant; we can easily see that the larger the population, the greater the number

of offspring and hence the more quickly the population grows. In the same way

the larger your bank account, the more interest you earn. Both these types of

growth exhibit a phenomenon called exponential growth. In this section we de-

velop the kinds of functions, called exponential functions, that model this type

of growth.

■ An Example of Exponential Growth

248 CHAPTER 3

■

Exponential Functions and Models

Bacteria are the most common organisms on the earth. Many bacterial species are

beneficial to humans; for example, they play an essential role in the digestive

process and in breaking down waste products. But some types of bacteria can be

deadly. For example, the Streptococcus A bacterium can cause a variety of dis-

eases, including strep throat, pneumonia, and other respiratory illnesses as well as

necrotic fasciitis (“flesh-eating” disease). Although bacteria are invisible to the

naked eye, their huge impact in our world is due to their ability to multiply rapidly.

Under ideal conditions the Streptococcus A bacterium can divide in as little as 20

minutes. So an infection of just a few bacteria can soon grow to such large num-

bers as to overwhelm the body’s natural defenses. How does such a massive infec-

tion happen?

Suppose that a person becomes infected with 10 streptococcus bacteria from

a sneeze in a crowded room. Let’s monitor the progress of the infection. If each

bacterium splits into two bacteria every hour, then the population doubles every

hour. So after one hour the person will have or 20 bacteria in his body. After

another hour the bacteria count doubles again, to 40, and so on. Of course, dou-

bling the number of bacteria means multiplying the number by 2. So if we start

10 * 2

Streptococcus A bacterium

112,000*2

Sebastian Kaulitzki/Shutterstock.com 2009

SECTION 3.1

■

Exponential Growth and Decay 249

Table 1 shows the number of bacteria at one-hour intervals for a 24-hour period. We

can see from the table that the bacterial population increases more and more rapidly

over the course of the day. What type of a function can we use to model such growth?

From the second column in the table we see that the population P after x hours is

given by

Model

This is called an exponential function, because the independent variable x is

the exponent. Let’s use this function to estimate the number of bacteria after

another half day has passed (36 hours in all). Replacing x by 36 in the model,

we get . This is almost a trillion bacteria. It’s no

wonder that unchecked infections can quickly cause serious damage to the

human body.

In Figure 1 we sketch a graph of the bacteria population P for x between 0 and

5; it would be difficult to draw a graph (to scale) for x between 0 and 24. Do you

see why?

P = 10

L 6.87 * 10

P = 10

table 1

Bacterial growth

Time Number of bacteria

1 hour

10 * 2 = 10

2 hours

10 * 2 * 2 = 10

3 hours

10 * 2 * 2 * 2 = 10

Time

(hours)

Number

bacteria

Number

bacteria

0 10 10

160

320

640

1280

2560

5120

10,240

20,480

40,960

81,920

163,840

327,680

655,360

1,310,720

2,621,440

5,242,880

10,485,760

20,971,520

41,943,040

83,886,080

167,772,160

200

100

12345

300

figure 1 Graph of bacteria population

■ Modeling Exponential Growth: The Growth Factor

In the preceding discussion we modeled a bacteria population by the function

, where 10 is the initial population. The base 2 is called the growth fac-

tor because the population is multiplied by the factor 2 in every time period. (In this

example the time period is one hour.)

f 1x2= 10

with 10 bacteria, the number of bacteria after the first, second, and third hours are

as follows.

250 CHAPTER 3

■

Exponential Functions and Models

example

Finding Models for Exponential Growth

Find a model for the following exponential growth situations.

(a) A bacterial infection starts with 100 bacteria and triples every hour.

(b) A pond is stocked with 5800 fish, and each year the fish population is multi-

plied by a factor of 1.2.

Solution

Since these populations grow exponentially, we are looking for a model of the form

(a) The initial population is 100, so C is 100. The population triples every hour, so

the one-hour growth factor is 3; that is, a is 3. Thus the model we seek is

where x is the number of time periods (hours) since infection.

(b) The initial population is 5800, so C is 5800. The population is multiplied by

1.2 every year, so the one-year growth factor is 1.2; that is, a is 1.2. Thus the

model we seek is

where x is the number of years (time periods) since the pond was stocked.

■ NOW TRY EXERCISES 25 AND 33 ■

Suppose a population is modeled by . The growth factor a is the

number by which the population is multiplied in every time period x. So increasing

f 1x2= Ca

f 1x2= 580011.2 2

f 1x2= 100

f 1x2= Ca

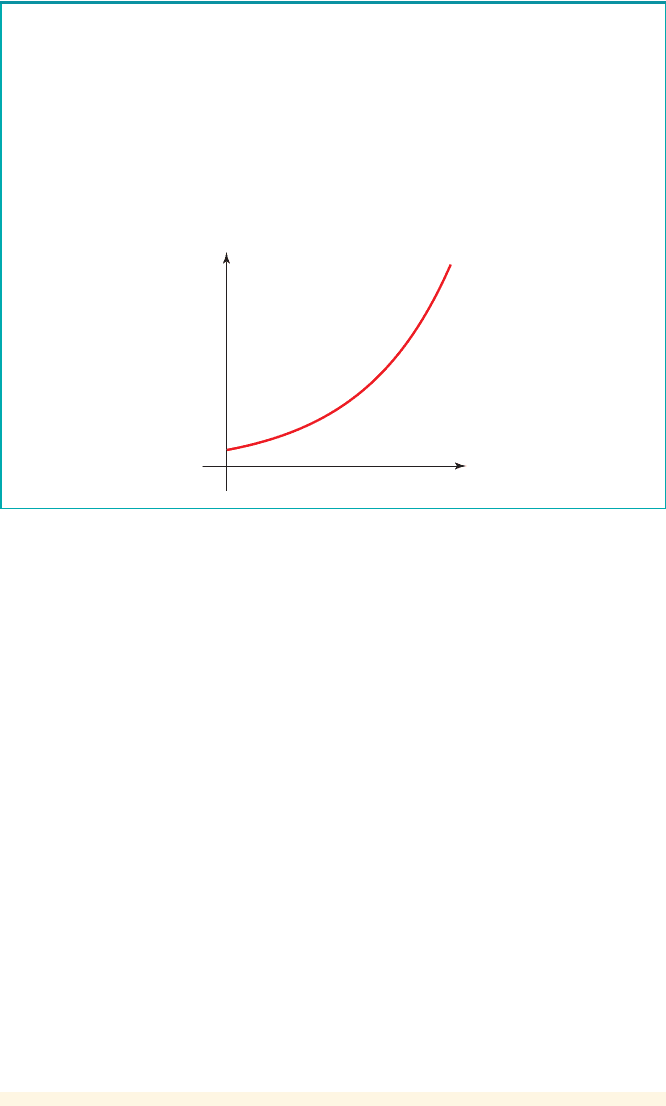
Exponential growth is modeled by a function of the form

■

The variable x is the number of time periods.

■

The base a is the growth factor, the factor by which is multiplied

when x increases by one time period.

■

The constant C is the initial value of f (the value when x is 0).

■

The graph of f has the general shape shown.

f 1x2

f 1x2= Ca

a 7 1

Exponential Growth Models: The Growth Factor

f 10 2= C

= C

f(x) = Ca˛

SECTION 3.1

■

Exponential Growth and Decay 251

x by one time period, we get , or

Let’s write this last formula in words:

If we know the population at two different times, we can use this formula to find the

growth factor, as the next example illustrates.

growth factor =

population after x + 1 time periods

population after x time periods

a =

f 1x + 12

f 1x2

f 1x + 12= a

f 1x2

example

Finding the Growth Factor

A chinchilla farm starts with 20 chinchillas, and after 3 years there are 128 chin-

chillas. Assume that the number of chinchillas grows exponentially. Find the 3-year

growth factor.

Solution

From the discussion preceding this example we have

■ NOW TRY EXERCISES 21 AND 39 ■

3-year growth factor =

population in year 3

population in year 0

128

= 6.4

■ Modeling Exponential Growth: The Growth Rate

The growth rate of a population is the proportion of the population by which it in-

creases during one time period. So if the population after x time periods is , then

the growth rate is

For instance, let’s suppose that a certain population increases by 40% each 1-year

time period and that is the population after x years (time periods). Then after one

more time period the population is

40% of is

Distributive Property

Simplify

So , and thus the growth factor is . In general,

for an exponential growth model we have

So and a = 1 + r.r = a - 1

r =

f 1x + 12- f 1x2

f 1x2

f 1x + 12

f 1x2

- 1 =

x +1

- 1 = a - 1

f 1x2= Ca

1 + 0.40 = 1.40f 1x + 12= 1.40 f 1x2

= 1.40 f 1x2

= 11 + 0.402 f 1x 2

0.40 f 1x 2f 1x 2 = f 1x 2+ 0.40 f 1x 2

f 1x + 1 2= 1population at x years 2+ 140% of the population 2

f 1x2

r =

f 1x + 12- f 1x2

f 1x2

The growth rate r is expressed as a

decimal. If the population increases

by 40% per time period, then the

growth rate is .r = 0.40

252 CHAPTER 3

■

Exponential Functions and Models

example

An Exponential Growth Model for a Rabbit Population

Fifty rabbits are introduced onto a small uninhabited island. They have no predators,

and food is plentiful on the island, so the population grows exponentially, increasing

by 60% each year.

(a) Find a function P that models the rabbit population after x years.

(b) How many rabbits are there after 8 years?

Solution

(a) The population grows by 60% each year, so the one-year growth rate r is 0.60.

This means that the one-year growth factor is

Since the initial population C is 50, the exponential growth model

that we seek is

Model

where x is measured in years.

(b) Replacing x by 8 in our model, we get

Replace x by 8

Calculator

So after 8 years there are about 2147 rabbits on the island.

■ NOW TRY EXERCISE 35 ■

L 2147.48

P 18 2= 50

11.602

P 1x2= 50

11.60 2

P 1x2= Ca

a = 1 + r = 1 + .60 = 1.60

For an exponential growth model, the growth factor a is greater than 1. The

growth rate r is positive and satisfies

a = 1 + r

r 7 0

The Growth Factor and the Growth Rate

In Exploration 4 of Chapter 6,

page 563, we use a “surge function”

to model the amount of a drug in the

body from the moment it is

ingested. Here, we model the decay

part of the surge function.

■ Modeling Exponential Decay

When a patient is injected with a drug, the concentration of the drug in the blood typ-

ically reaches a maximum quickly, but then as the liver metabolizes the drug, the

amount remaining in the bloodstream decreases exponentially. For example, suppose

a patient is injected with 10 mg of a therapeutic drug. It is known that 20% of the

drug is expelled by the body each hour, so after one hour 80% of the drug remains

in the body. The table below shows the amount of the drug remaining at the end of

1, 2, and 3 hours.

Time Amount remaining

1 hour

10 * 0.80 = 10

10.80 2

2 hours

10 * 0.80 * 0.80 = 10

10.80 2

3 hours

10 * 0.80 * 0.80 * 0.80 = 10

10.80 2

SECTION 3.1

■

Exponential Growth and Decay 253

From the pattern in the table we see that the amount remaining after x hours is mod-

eled by

This model has the same form as the model for exponential growth, except that the

“growth factor” (0.80) is less than 1, so the values of the function get smaller (instead of

larger) as time increases. Also, the “growth rate” is .

The negative growth rate indicates that 20% of the drug is subtracted from (in-

stead of added to) the body. We use the terms exponential decay, decay factor, and de-

cay rate to describe this situation.

- 0.20

r = a - 1 = 0.80 - 1 =-0.20

m 1x2= 10

10.80 2

Exponential decay is modeled by a function of the form

■

The variable x is the number of time periods.

■

The decay factor is a, where a is a positive number less than 1.

■

The decay rate r satisfies , so the decay rate is a negative

number.

■

The graph of f has the general shape shown.

a = 1 + r

f 1x2= Ca

0 6 a 6 1

Exponential Decay Models

f(x) = Ca˛

example

An Exponential Decay Model for a Medication

A patient is administered 75 mg of a therapeutic drug. It is known that 30% of the

drug is expelled from the body each hour.

(a) Find an exponential decay model for the amount of drug remaining in the

patient’s body after x hours.

(b) Use the model to predict the amount of the drug that remains in the patient’s

body after 4 hours.

Solution

(a) The amount of the drug decreases by 30% each hour, so the decay rate r is

. This means that the decay factor is

a = 1 + r = 1 + 1- 0.302= 0.70

- 0.30