Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов
Подождите немного. Документ загружается.

Теория поля
61
2).
),,(
321
ccca =
,
=
adiv
0
321
=
∂
∂
+
∂
∂
+
∂
∂
c
z
c
y
c
x
.
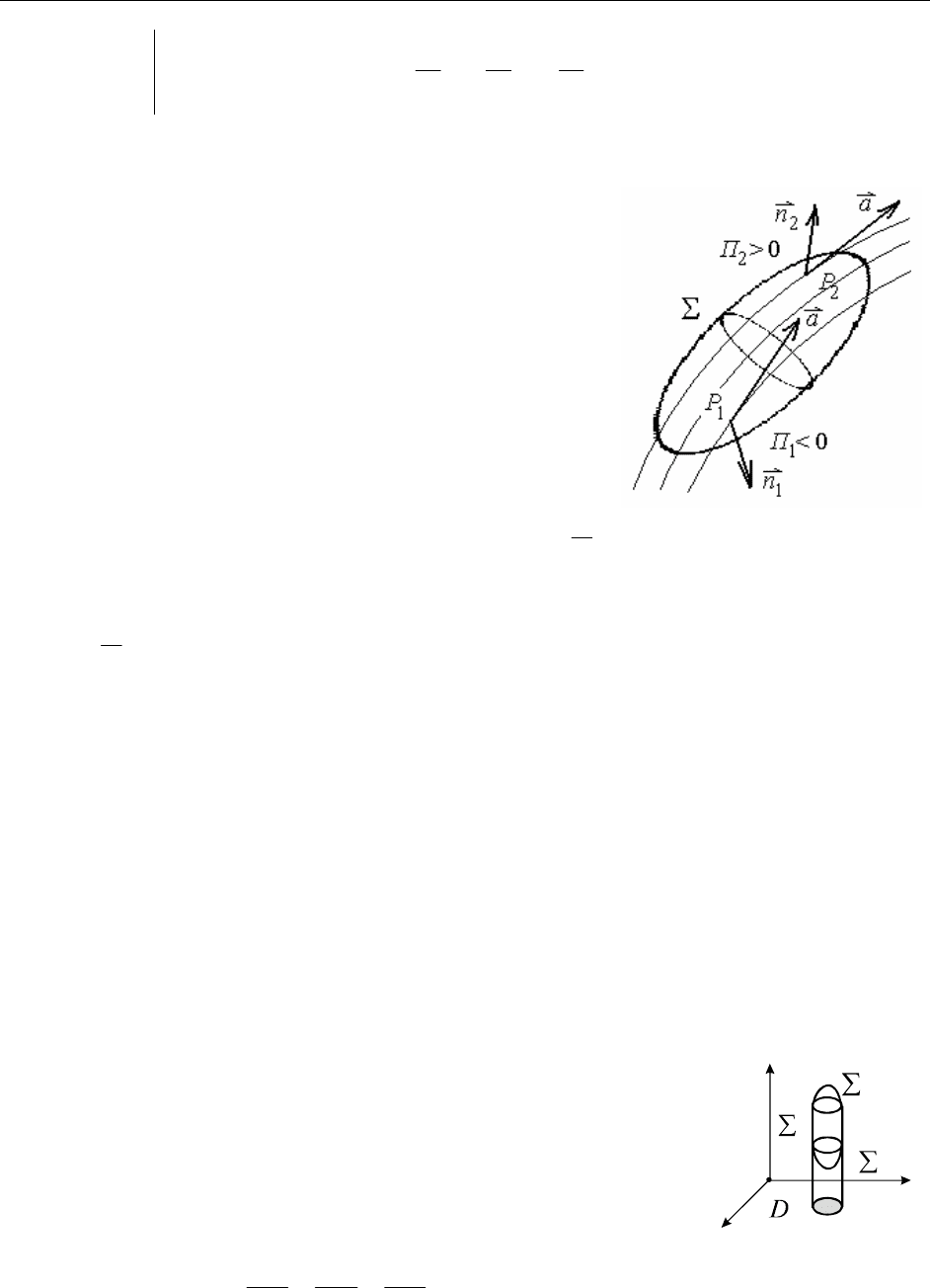
7.6. Физический смысл потока через замкнутую поверхность
Рассмотрим замкнутую поверхность
Σ
, огра-
ничивающую объем G в векторном поле
()aa= P
скоростей течения несжимаемой жидкости.
Поток вектора
()aaP=
через поверхность
Σ
,
равен количеству жидкости, проте-
кающей через поверхность
в единицу времени.
Обозначим единичный вектор внешней нормали
. Векторные линии входят и выходят из замкну-
той поверхности
. В точке угол
(, )ad
Σ
Π
=
∫∫
σ
1
Σ
0
n
Σ
P
0
(, )
2
an
π
>
;
это означает, что жидкость втекает внутрь поверхности. В точке выхода
2
P
0
(, )
2
an
π
<
, следовательно, жидкость вытекает. Поток векторного поля
a
че-
рез замкнутую поверхность
численно равен разности потоков жидкости,
втекающей и вытекающей в единицу времени со скоростью
в пространст-
венную область G, ограниченную
Σ
a
Σ
.
Пусть П>0, следовательно, жидкости вытекает больше, чем втекает, в
области G есть
источники поля.
Если П<0, втекает жидкости больше, чем вытекает, то в G есть
стоки.
Если П=0, то в области G источников и стоков или нет, или они компен-
сируют друг друга.
7.7. Теорема Остроградского - Гаусса
Если в некоторой области G трёхмерного про-
странства, ограниченной замкнутой кусочно-
гладкой поверхностью
, задано непрерывно диф-
ференцируемое векторное поле
Σ
x
yz
aaiaja=++k
Z
2
1
3
X
Y
V
xy
Г
,
то поток векторного поля
через внешнюю сторо-
ну замкнутой поверхности
равен тройному инте-
гралу от функции
a
Σ
y
x
z
a
aa
x
yz
∂
⎛
∂
⎞
∂
⎜⎟
++
∂
∂∂
⎝⎠
по области G,
ограниченной поверхностью
:
Σ

Лекция 5 - 9
62
()
y
x
z
G
a
a
a
a d dxdydz
xyz
Σ
Πσ
∂
⎛⎞
∂
∂
=⋅= ++
⎜⎟
∂∂∂
⎝⎠
∫∫ ∫∫∫
,
где символ
обозначает интеграл по замкнутой поверхности.
Σ
∫∫
Доказательство:
Часть 1.
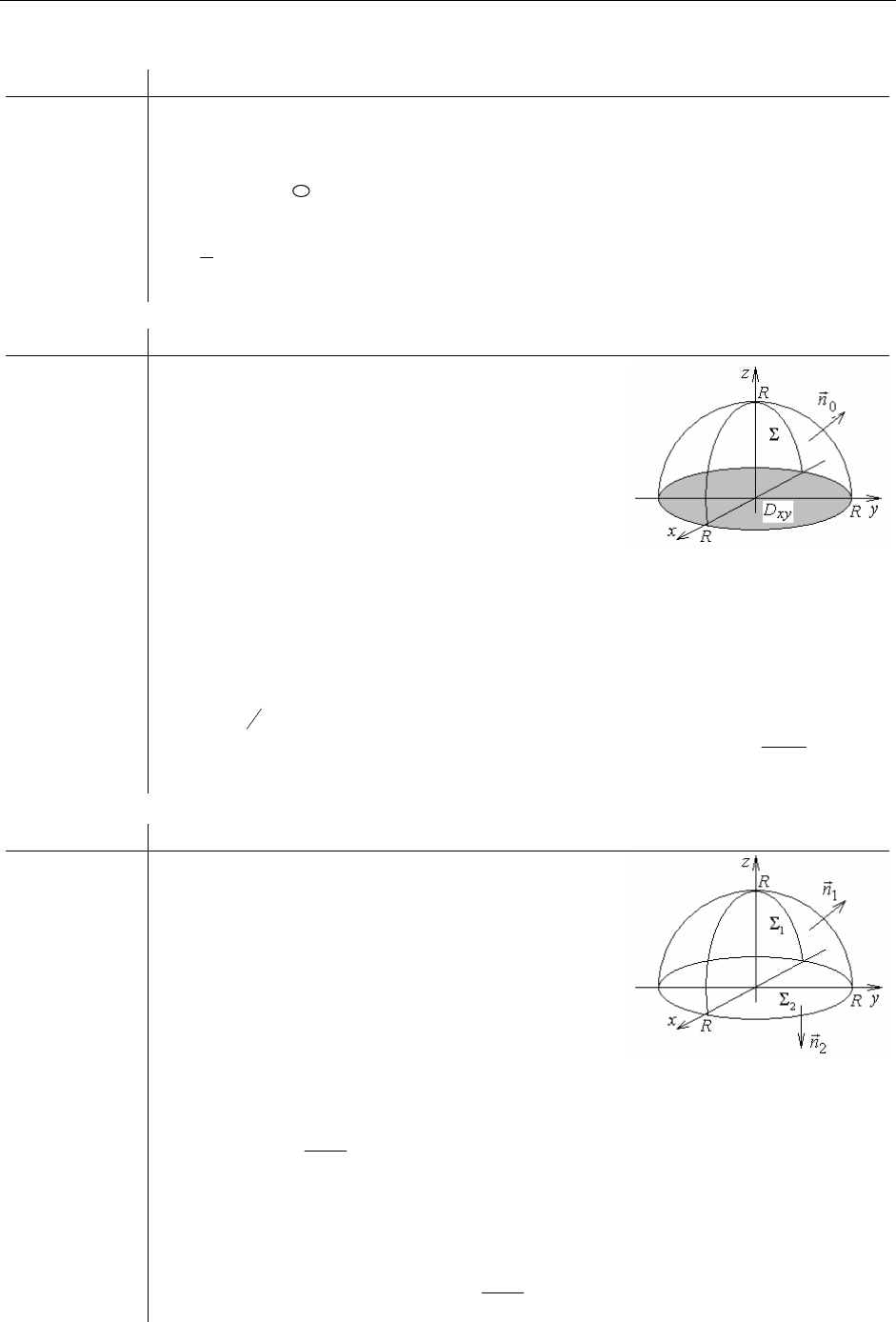
Рассмотрим область G, правильную в направлении оси Oz, которую бу-
дем называть
элементарной H
z
областью. Это означает, что снизу и сверху
она ограничена поверхностями:
1
Σ
:
1
(, )zzxy
=
и
2
Σ
:
2
(, )zzxy
=
соответст-
венно, а сбоку цилиндрической поверхностью
3
Σ
с образующими, парал-
лельными оси Oz, и направляющей Г.
Рассмотрим одно слагаемое:
2
1xy
z
zz
GDz
aa
dxdydz dxdy dz
zz
∂∂
==
∂∂
∫∫∫ ∫∫ ∫
2
1
(, )
(, ,)
(, )
xy
z
D
zxy
dxdya x y z
zxy
=
∫∫
=
{
}
21
(, , (, )) (, , (, )
xy
zz
D
dxdyaxyzxy axyzxy−
∫∫
=
=
2
(, , (, ))
xy
z
D
axyzxydxdy
−
∫∫
1
(, , (, ))
xy
z
D
a x y z x y dxdy
∫
∫
=…
{на
2
Σ
cos 0
γ
>
, а на
1
Σ
cos 0
γ
<
.
Учитывая, что
cosdxdy d
γ
σ
=
, получаем:
на
:
2
Σ
cosdxdy d
γ
σ
=
,
на
:
1
Σ
cosdxdy d
γ
σ
=−
} …=
2
(, ,)cos
z
axyz d
γ
σ
Σ
∫
∫
+
1
(, ,)cos
z
axyz d
γ
σ
Σ
∫
∫
=…
Добавим интеграл по
3
Σ
3
(, ,)cos
z
axyz d
γ
σ
Σ
∫∫
в полученную сумму, так как на
co
3
Σ
s
γ
всюду равен нулю, а следовательно, и
3
(, ,)cos 0
z
axyz d
γσ
Σ
=
∫
∫
.
Тогда
…=
2
(, ,)cos
z
axyz d
γ
σ
Σ
∫∫
+
1
(, ,)cos
z
axyz d
γ
σ
Σ
∫
∫
+
3
(, ,)cos
z
axyz d
γ
σ
Σ
∫
∫
=
123
(, ,)cos
z
axyz d
γ
σ
Σ+Σ+Σ
=
∫∫
=
(, ,)cos
z
axyz d
γ
σ
Σ
∫
∫
.
Часть 2.
Рассмотрим пространственную область G, которую можно разбить на n
элементарных областей H
z
типа, т.е. . Докажем, что и в этом случае
справедлива теорема Остроградского-Гаусса.
1
n
k
GG
k
=
=
∪

Теория поля
63
Пусть , , - нижняя, верхняя и боковая части поверхности
()
1
k
Σ
()
2
k
Σ
()
3
k
Σ
(
)
k
Σ
,
ограничивающей область
,
k
G
тогда
z
G
a
dxdydz
z
∂
=
∂
∫∫∫
1
k
n
z
k
G
a
dxdydz
z
=
∂
=
∂
∑
∫∫∫
1
1
cos
k
n
z
k
ad
γ
σ
=
Σ
⎧
⎪
=
⎨
⎪
⎩
∑
∫∫
+
2
cos
k
z
ad
γ
σ
Σ
∫∫
+
3
cos
k
z
ad
γ
σ
Σ
⎫
⎪
⎬
⎪
⎭
∫∫
=cos
z
ad
γ
σ
Σ
∫∫
,
так как интегралы по
()
3
k
Σ
равны нулю, а по поверхности
(
)
1
k
Σ
и составля-
ют в сумме интеграл по поверхности
()
2
k
Σ
(
)
k
Σ
.
Часть 3.
Аналогично для H
x
и H
y
областей справедливо:
cos
y
y
G
a
dxdydz a d
y
β
σ
Σ
∂
=
∂
∫∫∫ ∫∫
; cos
x
x
G
a
dxdydz a d
x
α
σ
Σ
∂
=
∂
∫∫∫ ∫∫
.
Складывая почленно, получаем утверждение теоремы
.
!
1). Координатная форма записи теоремы Остроградского-Гаусса имеет
вид:
( cos cos cos )
xyz
aaad
α
βγσ
Σ
+
+=
∫∫
()
y
xz
G
a
aa
dxdydz
xyz
∂
∂∂
=++
∂∂∂
∫∫∫
,
где
cos ,cos ,cos
α
βγ
- координаты единичного вектора внешней норма-
ли.
2). Используя обозначение дивергенции, формулу Остроградского-
Гаусса можно записать в виде:
(
)
(
)
0
GG
a n d diva dxdydz a dxdydz
σ
⋅= =∇⋅
∫∫∫ ∫∫∫
Σ
∫∫
div
.
Поток векторного поля (вектора) через внешнюю сторону замкнутой по-
верхности
равен тройному интегралу от
Σ
a
по пространственной
области G, ограниченной поверхностью
Σ
.
Лекция 5 - 9
64
Применение теоремы Остроградского - Гаусса
Пример:
Вычисление объемов.
Пусть
;
rzyxa
=),,( (, ,)rx
y
z
=
;
() () 1 1 1 3div a div r
=
=++=
.
∫∫∫ ∫∫
Σ
++=
G
dzdydxdxdydz
σγσβσα
coscoscos3
,
1
()
3
V xdydz ydxdz zdxdy
Σ
=++
∫∫
.
Пример:
Вычисление потоков.
Вычислить поток поля
kzjyixa
222
++=
через замкнутую поверхность
:
Σ
()
222
,
00.
2
x
yzR
zz
⎧
++=
⎪
⎨
=≥
⎪
⎩
Решение:
()ad
Σ
Πσ
=⋅
∫
∫
=
∫∫∫
G
dxdydzadiv
=
=…
dxdydzzyx
G
)222(
∫∫∫
++
{перейдём в сферическую систему координат}
…=
2
2
2
00 0
sin (2 cos sin 2 sin sin 2 cos )
R
ddrdrr r r
π
π
ϕ
θθ ϕθ ϕθ θ
++
∫∫ ∫
=
2
4
R
π
.
Пример:
Найти поток поля
kzjyixa
222
++=
через
внешнюю сторону полусферы:
222 2
,
:
0.
x
yzR
z
Σ
⎧
++=
⎨
≥
⎩
Решение:
Воспользуемся результатами предыдущей за-
дачи. Замкнем поверхность
1
Σ
поверхностью
, которая представляет собой часть плоскости XOY.
2
Σ
4
12
2
R
ПП П
π
=+=
,
12
ППП
=
−
,
(
)
2
20
Σ
an d
Π
σ
=⋅
∫∫
=
=…{
222
0
(,,)(0,0,1)an x y z z⋅= ⋅ −=−
2
}… =
2
2
Σ
0zd
σ
−
=
∫∫
,
т.к. на
и
2
Σ
0z =
12
ППП
=
−
=
4
2
R
π
.
7.8. Инвариантное определение дивергенции
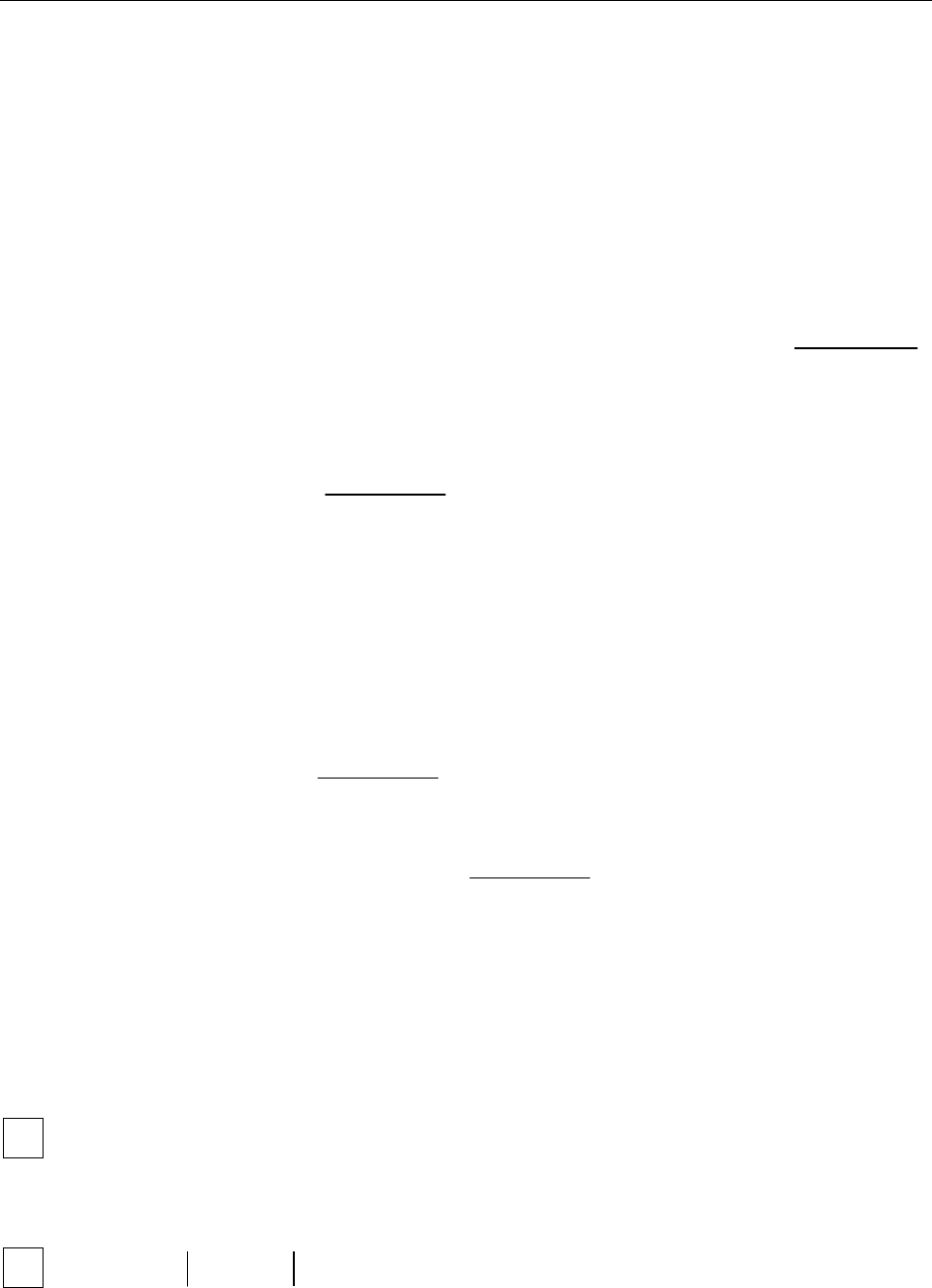
Теория поля
65
Пусть
- векторное поле, удовлетворяющее условию теоремы
Остроградского – Гаусса. Пусть точка M - произвольная точка области G.
Выберем поверхность
, охватывающую область G. Из теоремы Остроград-
ского – Гаусса следует, что
()aaP=
Σ
0
()
G
a n d diva dxdydz
σ
Σ
⋅=
∫∫ ∫∫∫
.
Воспользуемся теоремой о среднем, согласно которой существует такая точ-
ка М
1
, принадлежащая G, что
(
)
1
|
M
diva V a d
σ
Σ
⋅= ⋅
∫∫
;
()
1
()
ad
diva M
V
σ
Σ
⋅
=
∫∫
,
где V –объем G. Пусть
стягивается в точку М, тогда М
Σ
1
→М, а
→
,
1
()diva M
()diva M
()
( ) lim
M
ad
diva M
V
σ
Σ
Σ→
⋅
=
∫∫
.
Поскольку правая часть выражения не зависит от системы координат (инва-
риантна), то инвариантно и данное определение дивергенции.
7.8.1. Физический смысл дивергенции
Поскольку величина
()ad
V
σ
Σ
⋅
∫∫
имеет смысл средней плотности потока
в пространственной области G, то
()
lim
M
ad
diva
V
σ
Σ
Σ→
⋅
=
∫∫
есть плотность пото-
ка в точке М.
Точки поля, в которых дивергенция положительна, т.е.
, называют источниками векторного поля, а точки, в
которых дивергенция отрицательна,
()0diva M
Π
>⇒ >
0
()0 0div a M
Π
<
⇒<
- стоками вектор-
ного поля.
С
Векторные линии векторного поля начинаются в точках поля с положи-
тельной дивергенцией, а заканчиваются в точках с отрицательной дивер-
генцией.
Величину
()div a M
называют мощностью источника или стока.
О

Лекция 5 - 9
66
8.1. Линейный интеграл в векторном поле
Рассмотрим кусочно-гладкую кривую L и дугу
AB (обозначение
1
i
−
i
i
A
1
i
A
−
1
i
−
∆
X
Z
Y
A
B∪
) и векторное поле
(,,)
x
yz
aaaa=
, непрерывное на L. Разобьем дугу
A
B∪
произвольным образом точками A
0
, A
1
, …A
n
на
n частей. Обозначим
- вектор, стягивающий кон-
цы дуги
i
r∆
1ii
A
A
−
∪
i
P
. Выберем точку
1ii
AA
−
∈
∪
i
. Найдём
скалярное произведение
(( ) )
i
aP r
⋅
∆
i
r∆
и просуммируем по всем участкам дуг
. Вычислим предел
1
(( ) )
n
ni
i
SaP
=
=⋅
∑
max 0
1
lim lim ( ( ) )
i
n
ni
nr
i
SaP
→∞ ∆ →
=
i
r
=
⋅∆
∑
.
О
Если этот предел существует и не зависит от способа разбиения дуги
A
B∪
на отдельные участки и о выбора точки Pт
i
, то он называется ли-
нейным интегралом вектора
a
по дуге
A
B∪
в направлении от А до В.
Обозначение:
. Координатная форма записи:
(, )
AB
adr
∪
∫
()
xyz
AB AB
a dr a dx a dy a dz
∪∪
⋅= + +
∫∫
=
(, ,) (, ,) (, ,)
xyz
AB
a xyzdx a xyzdy a xyzdz
∪
++
∫
,
()
AB
adr
∪
⋅
∫
=
max 0
1
lim ( ( ) )
i
n
ii
r
i
aP r
∆→
=
⋅
∆
∑
.
!
Линейный интеграл иногда называют криволинейным интегралом вто-
рого рода.
8.2. Свойства линейного интеграла
1. Свойство линейности:
(( ) )
AB
abdr
λµ
∪
+⋅
∫
=
()
AB
adr
λ
∪
⋅
∫
+
()
AB
bdr
µ
∪
⋅
∫
.
2. Свойство аддитивности:
=
()
AB
adr
∪
⋅
∫
()
AC
adr
∪
⋅
∫
+
()
CB
adr
∪
⋅
∫
.
3. При изменении направления интегрирования
линейный интеграл меняет знак:
()
AB
adr
∪
⋅
∫
=
()
BA
adr
∪
−
⋅
∫
.
C
X
Z
Y
C
Свойства 1-3 доказываются из определения.

Теория поля
67
!
Определение криволинейного интеграла остается спра-
ведливым, если начальная и конечная точка совпадают.
+
О
Криволинейный интеграл по замкнутому контуру назы-
вается
циркуляцией векторного поля по замкнутому
контуру:
.
()
L
Cad=⋅
∫
r
Положительным направлением обхода считается то, при котором об-
ласть, ограниченная контуром, остается слева.
8.3. Вычисление линейного интеграла
Пусть
A
BL∪
и кривая L задана параметрическими уравнениями:
∈
)
()
:(
()
x
xt
L
yyt
zzt
=
⎧
⎪
=
⎨
⎪
=
⎩
,
при этом при
t
имеем точку
0
t=
0
()
00
0
00
()
:
()
x
xt
A
yyt
zzt
=
⎧
⎪
=
⎨
⎪
=
⎩
, при
tt
1
=
11
11
11
()
:(
()
)
x
xt
B
yyt
zzt
=
⎧
⎪
=
⎨
⎪
=
⎩
,
тогда
()
AB
adr
∪
⋅
∫
= =
=
,
(, ,) (, ,) (, ,)
xyz
AB
a xyzdx a xyzdy a xyzdz
∪
++
∫
1
0
{ ( (), (), ()) () ( (), (), ()) () ( (), (), ()) ()}
t
xyz
t
a xt yt zt xt a xt yt zt yt a xt yt zt zt dt⋅+ +
∫
где точки над переменными
,,
x
yz
означают дифференцирование по пере-
менной t.
Пример:
Дано:
a kyjxiz
++=
, L:
cos
sin
2
x
Rt
yR t
t
z
π
⎧
⎪
=
⎪
=
⎨
⎪
⎪
=
⎩
, A(t
0
=0), B(t
1
=2
π
).
Вычислить линейный интеграл по
A
B∪
.
Решение:
(, )
AB AB
a dr zdx xdy ydz
∪∪
=
++
∫∫
=
2
2
0
1
( sin ) cos cos sin .
22
t
RtR tR t Rtdt RR
π
π
ππ
⎧⎫
=−+ + =
⎨⎬
⎩⎭
∫
+
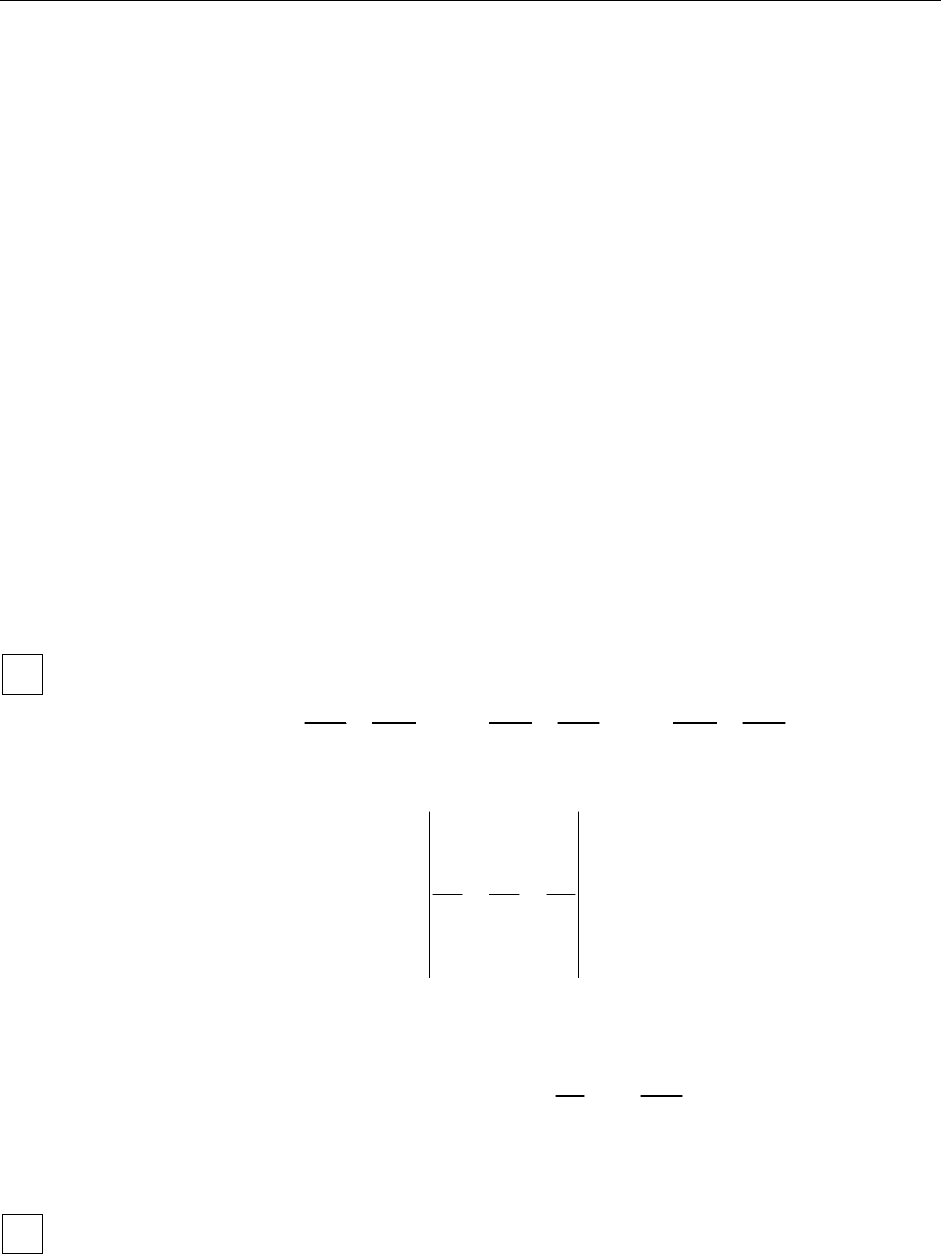
Лекция 5 - 9
68
8.4. Физический смысл линейного интеграла
Рассмотрим в качестве поля
a
силу
F
, приложенную к материальной
точке Р и меняющуюся о величине и направлению при изменении местопо-
ложения точки Р.
п
)(
A
Fdr=⋅
- работа по перемещению материальной точки
по участку
, тогда ()
dr
AB
Fdr A
∪
⋅=
∫
- работа силы
F
по перемещению мате-
риальной точки по дуге АВ.
8.5. Ротор (вихрь) векторного поля
Пусть вектор-функция
() ( , , )
x
yz
aaP aaa==
является непрерывно диф-
ференцируемой в каждой точке области определения.
Ротором векторного поля (вектора)
a
называется вектор, обозначаемый
символом
rot a
, равный
О
yy
x
x
zz
aa
aa
aa
t a i j k
yz zx xy
∂∂
⎛⎞ ⎛
∂∂
∂∂
⎛⎞
=−+−+−
⎜⎟
⎜⎟ ⎜
∂∂ ∂∂ ∂∂
⎝⎠
⎝⎠ ⎝
ro
⎞
⎟
⎠
.
Это выражение удобно записать в виде символического определителя
x
yz
ijk
rota
x
yz
aaa
∂
∂∂
=
∂
∂∂
,
который вычисляется разложением по первой строке (по базисным векторам
); произведение частных производных на компоненты вектора понима-
ется как дифференцирование последних, т.е.
,,ijk
x
x
a
a
zz
∂
∂
=
∂
∂
и т.п. С использова-
нием оператора набла
rot a a
⎡
⎤
=∇×
⎣
⎦
.
Если в некоторой точке поля
0rot a
=
, то поле в этой точке называется
безвихревым.
!

Теория поля
69
Пример:
2
()()( )axziyzjxzk=+ ++ + +
.
−+
∂
∂
−+
∂
∂
=
+++
∂
∂
∂
∂
∂
∂
= ))()((
2
2
zy
z
zx
y
i
zxzyzx
zyx
kji
arot
2
j( (x z) (x z))
x
z
∂∂
−+−++
∂∂
=+
∂
∂
−+
∂
∂
))()(( zx
y
zy
x
k
=
kxji
0)12( +−−−
=
{
}
1, 1 2 , 0x−−
.
8.5.1. Свойства ротора (вихря)
1. Линейность: , где λ и
()rot a b rot a rot b
λµ λ µ
+=⋅ +⋅
µ
- некоторые по-
стоянные. Иначе,
()ab a b
λµ λ µ
⎡⎤ ⎡
⎡⎤
∇× + = ∇× + ∇×
⎣⎦
⎣⎦ ⎣
⎤
⎦
.
2. Пусть
- скалярное поле, тогда
(, ,)uuxyz=
()rot u a
⋅
=
=
[
.
]
grad u a u rot a×+⋅
В векторных обозначениях:
[()][ ][ua u a u a]
∇
×=∇×+∇×
.
Доказательство:
[()]ua∇× =
xyz
ijk
x
yz
ua ua ua
∂∂∂
=
∂∂∂
() ()
zy
iua ua
yz
⎛⎞
∂∂
−
⎜⎟
∂∂
⎝⎠
() ()
zx
jua ua
xz
∂∂
⎛⎞
−−
⎜⎟
∂∂
⎝⎠
+
() ()
yx
kua ua
xy
⎛
⎞
∂∂
+−
⎜
⎟
∂∂
⎝
⎠
=
zy zx yx
ui a a j a a k a a
yz xz xy
⎧⎫
⎛⎞ ⎛
∂∂ ∂∂ ∂∂
⎛⎞
⎞
−
−−+−
⎨⎬
⎜⎟
⎜⎟ ⎜
∂∂ ∂∂ ∂∂
⎝⎠
⎝⎠ ⎝
⎩⎭
+
⎟
⎠
+
zy
uu
ia a
yz
⎛⎞
∂∂
−
⎜⎟
∂∂
⎝⎠
zx
uu
ja a
xz
∂∂
⎛⎞
−−
⎜⎟
∂∂
⎝⎠
yx
uu
ka a
xy
⎛⎞
∂∂
+−
⎜⎟
∂∂
⎝⎠
=
[
]
()urota gradu a
⋅
+×
.
Пример:
[]
1
,()[ ] [ ]
r
a const rot r a grad r a r rota grad r a a r a
rr
⎡⎤
==×+=×=×=
⎢⎥
⎣⎦
×

Лекция 5 - 9
70
8.6. Теорема Стокса
(устанавливает связь между циркуляцией и ротором)
Циркуляция непрерывно дифференцируемого векторного поля
x
yz
aai ajak=++
по произвольному кусочно-гладкому контуру L вычисля-
ется по формуле
xyz
L
adx ady adz++
∫
=
cos
y
z
a
a
yz
α
Σ
⎧∂
⎛⎞
∂
−
+
⎨
⎜⎟
∂∂
⎝⎠
⎩
∫∫
+
cos
xz
aa
zx
β
∂∂
⎛⎞
⎜⎟
+
−
∂∂
⎝⎠
cos
y
x
a
a
d
xy
γ
σ
∂⎫
⎛⎞
∂
−
⎬
⎜⎟
.
∂∂
⎝⎠
⎭
При этом выбор стороны поверхности
Σ
и направление обхода контура L со-
гласованы (по правилу винта).
Доказательство:
Для доказательства сгруппируем слагаемые пра-
вой части с одинаковыми координатами вектора
в
a
:
()rota d
σ
Σ
⋅
∫∫
=
cos cos
xx
aa
d
zy
β
γσ
⎛⎞
∂∂
−
⎜⎟
∂∂
⎝⎠
Σ
∫∫
+
0
1
t
2
t
2
()
yx
1
()
yx
X
Z
Y
xy
+
cos cos
yy
aa
d
xz
γ
ασ
Σ
∂∂
⎛⎞
−
⎜⎟
∂∂
⎝⎠
∫∫
+
cos cos
zz
aa
d
yx
α
βσ
Σ
⎛⎞
∂∂
−
⎜⎟
∂∂
⎝⎠
∫∫
.
Рассмотрим первый из интегралов:
1
(cos cos)
xx
aa
I
d
zy
β
γσ
Σ
∂∂
=−
∂∂
∫∫
=
cos
()c
cos
xx
aa
d
zy
os
β
γ
σ
γ
Σ
∂
∂
−
∂∂
∫∫
.
Пусть поверхность
однозначно проектируется на координатную
плоскость
, т.е. любая прямая, параллельная оси , пересекает ее не
более чем в одной точке; тогда
Σ
Oxy
Oz
Σ
:
(, )zzxy
=
,
2
2
|| 1
zz
n
xy
⎛⎞
∂∂
⎛⎞
=
++
⎜⎟
⎜⎟
∂∂
⎝⎠
⎝⎠
;
0
2
2
,,1
1
zz
xy
n
zz
xy
⎧⎫
∂∂
−
⎨⎬
∂∂
⎩⎭
=
⎛⎞
∂∂
⎛⎞
++
⎜⎟
⎜⎟
∂∂
⎝⎠
⎝⎠
,
cos
cos
z
y
β
γ
∂
=
−
∂
, так как угол между ортом и осью
0
n
