Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов
Подождите немного. Документ загружается.


Числовые ряды
91
2). Рассмотрим ряд
∑
∞
=1
2
.
1
n
n
Для него также
.1
)1(
limlim
2
2
1
=
+
=
∞→
+
∞→
n
n
u
u
n
n
n
n
Срав-
ним члены исследуемого ряда со сходящимся рядом
∑
∞
=
+
1
)1(
1
n
nn
(доказа-
но ранее):
∑∑
∞
=
∞
=
+
=
10
22
,
)1(
11
nn
nn
2
11
(1) (1
nnn
<
)
+
+
, значит,
∑
∞
=1
2
1
n
n
сходится.
Пример:
Исследуйте на сходимость ряды:
1)
.
!
1
1
∑
∞
=n
n
,
321
1
!
1
nn
u
n
…⋅⋅
==
,
)1(321
1
)!1(
1
1
+⋅⋅
=
+
=
+
nnn
u
n
…
0
1
1
limlim
1
=
+
=
∞→
+
∞→
nu
u
n
n
n
n
.
Ряд сходится.
2)
∑
∞
=
+
1
.
2
12
n
n
n
n
Вычислим
1
2
2
2
1
2
2
112
32
limlim
2
1
2
1
<==⋅
+
⋅
+
+
=
+
∞→
+
∞→
n
n
n
n
n
n
n
n
n
n
u
u
,
ряд сходится.
3)
∑
∞
=
+
1
)!3(
)!12(!
n
n
nn
можно убедиться, что , выполняется необ-
ходимый признак сходимости.
0
n
u →
Вычислим
=
++
+
+
+
∞→
)!12(!)!33(
)!3()!1)1(2()!1(
lim
nnn
nnn
n
(1)!(23)!(3)!
lim
(3 3)! !(2 1)!
n
nnn
nnn
→∞
+
+
=
++
=
+++
+
++
∞→
)13)(23)(33(
)32)(22)(1(
lim
nnn
nnn
n
122 4
.1
333 27
⋅
⋅= <
, исследуемый ряд схо-
дится.
11.1.2. Признак Коши
Если 1) и 2) существует
0>
n
u
,lim lu
n
n
n
=
∞→
тогда
1
сходится, если 1,
расходится, если 1,
признак не дает ответа, если 1.
n
n
l
ul
l
∞
=
<
⎡
⎢
>
⎢
⎢
=
⎣
∑
Доказательство:
0
nn
nn
n
lim u l N : n N u l ,
ε
ε
→∞
∃=⇒∀>∃∀>⇒−<
n
n
l.lu
ε
ε
−
<<+

Лекции 10 - 11
92
1) Выберем
.1<l
ε
так, чтобы
,ql
=
+
ε
.1
<
q
Тогда
,
n
n
nn
uquq<<
.
Так как
сходится при
∑
∞
=1n
n
q
1,q
<
то и - сходится.
∑
∞
=1n
n
u
2)
Выберем
.1>l
ε
так, чтобы
.1>
−
=
ε
lq
Тогда
n
n
lu
ε
−<
и расходится при
⇒
1:
n
n
uq>>lim 0
n
n
u
→∞
≠
1
n
n
u
∞
=
∑
1.l >
3)
. Признак ответа не дает, ряд может как сходиться, так и рас-
ходиться.
1=l
Рассмотрим те же примеры, что и при рассмотрении признака
Даламбера.
∑
∞
=1
1
n
n
. Пусть
1
n
n
C
n
=
,
ln
ln 0
n
n
n
C
n
→∞
=
−⎯⎯⎯→
,
1
n
n
C
→∞
=
⎯⎯⎯→
,
но ряд расходится.
2
1
1
n
n
∞
=
∑
. Пусть
2
1
n
n
C
n
′
=
,
2ln
ln 0
n
n
n
C
n
→∞
′
=
−⎯⎯⎯→
,
1
n
n
C
→∞
′
=
⎯⎯⎯→
,
но ряд сходится.
Пример:
Исследуйте на сходимость ряд
∑
∞
=
⎟
⎠
⎞
⎜
⎝
⎛
+
1
.
12
n
n
n
n
1
2
1
1
2
1
lim
12
lim
12
lim <=
+
=
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
∞→∞→∞→
n
n
n
n
n
nn
n
n
n
, ряд сходится.
11.1.3. Интегральный признак сходимости
Пусть 1) и 2) , то есть члены ряда не возрастают,
0>
n
u
1+
≥
nn
uu
3)
−)(n
f
такая непрерывная не возрастающая функция, что
.)(
n
unf
=
Тогда ряд и несобственный инте-
грал
∑
∞
=
1n
n
u
1
()
f
xdx
∞
∫
либо одновременно сходятся,
либо одновременно расходятся.
Доказательство:
Изобразим ситуацию геометрически.
Площадь криволинейной трапеции, ограни-
ченной прямыми
1
x
=
,
1
x
n
=
+
,
0y
=
и
графиком функции
(
)
yfx=
, равна
1
1
1
()
n
n
I
fxdx
+
+
=
∫
.

Числовые ряды
93
Площадь ступенчатой фигуры, описанной около этой криволиней-
ной трапеции, равна частичной сумме ряда
12nn
Suu u
=
+++…
.
Площадь ступенчатой фигуры, вписанной в ту же криволинейную
трапецию, равна
11 2 3nn
Suuu u
1
+
+
−=+++…
.
Последовательность частичных сумм
{
}
n
S
и последовательность
{
}
n
I
монотонно возрастают:
11
0
nnn
SSn
++
−
=>
,
1
1
() 0
n
nn
n
II fxdx
+
+
−
=>
∫
.
Очевидно,
11 1nn
SuI S
++n
−
<<
.
Переходя к пределам, получаем
11 1
lim lim lim
nn
nn
Su I S
++
→∞ →∞ →∞
n
n
−
≤≤, или, так
как
и
1
lim lim
nn
nn
SS
+
→∞ →∞
=
1
lim lim
nn
nn
I
I
+
→∞ →∞
= , то
1
lim lim lim
nn
nnn
Su I S
→∞ →∞ →∞
n
−
≤≤.
1). Если интеграл сходится,
1
lim ( )
n
n
II fxdx
∞
→∞
=
=
∫
<∞
, то
, ряд сходится. Если ряд сходится, , то
, интеграл сходится.
1
lim
n
n
SIu
→∞
≤+ <∞
lim
n
n
SS
→∞
=<∞
lim
n
n
IS
→∞
≤<∞
2). Если интеграл расходится,
, то и (так
как
), ряд расходится. Если ряд расходится, , то
, и, так как
n
n
I
→∞
⎯⎯⎯→∞
n
n
S
→∞
⎯⎯⎯→∞
nn
SI>
n
n
S
→∞
⎯⎯⎯→∞
()
1n
n
Su
→∞
−⎯⎯⎯→∞
1nn
I
Su>−
, , интеграл расходит-
ся.
n
n
I
→∞
⎯⎯⎯→∞
Пример:
Исследуйте на сходимость ряды:
1)
∑
∞
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++
1
2
)1(ln)1(
1
n
nn
;
)1(ln)1(
1
)(
2
++
=
xx
xf
.
∫∫
∞
∞→
∞
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−=
+
+
=
++
1
1
2
1
2
)1ln(
1
lim
)1(ln
))1(ln(
)1(ln)1(
a
a
x
x
xd
xx
dx
=
,
2ln
1
)1ln(
1
2ln
1
lim =
⎥
⎦
⎤
⎢
⎣
⎡
+
−
∞→
a
a
исследуемый ряд сходится.
2)
()()
55
1
23
n
nn
u.
nlnn
∞∞
==
=
−−
∑∑
Исследуем на сходимость вспомогательный ряд
55
1
(3)ln(3)
n
nn
v
nn
∞∞
==
=
−−
∑∑
с помощью интегрального признака.
Несобственный интеграл
5
52
2ln( 3)
(3)ln(3)
dx dt
x
xx t
∞∞
∞
=
=−
−−
∫∫
=∞

Лекции 10 - 11
94
расходится, следовательно, расходится вспомогательный ряд
.
5
n
n
v
∞
=
∑
Так как
1
2
3
limlim =
−
−
=
∞→∞→
n
n
v
u
n
n
n
n
, то по второй теореме сравнения ис-
ходный ряд также расходится.
3)
∑
∞
=1
1
n
n
;
x
xf
1
)( =
.
∞==
∫
∞
∞→
1
1
lnlim
1
a
a
xdx
x
, исследуемый ряд расходится.
Заметим, что для оценки остатка ряда
с положительными чле-
нами удобно пользоваться интегральным признаком сходимости.
Если этот признак применим к ряду
то имеет место оценка
.
n
R
∑
∞
=1
),(
n
nf
∫∫
∞
+
∞
<<
1
)()(
nn
n
dxxfRdxxf
Пример:
Сколько членов ряда
∑
∞
=1
2
1
n
n
нужно взять, чтобы получить значение
суммы ряда с точностью до 0,001?
Здесь
,
1
)(
2
x
xf =
,
11
2
∫
∞
∞
=−=
n
n
nx
x
dx
по условию
,001,0
1
>
n
зна-
чит нужно взять 1001 член.
,1000>n
11.2. Знакопеременные ряды
Рассмотрим ряды, содержащие бесконечное множество положи-
тельных и бесконечное множество отрицательных членов. Такие ряды
называются знакопеременными.
Если для знакопеременного ряда
Т
12nn
uuu u=++++……
1
n
∞
=
∑
(1)
сходится ряд, составленный из абсолютных величин его членов,
12
1
n
n
uuu u
∞
=
=++++
∑
…
n
…
, (2)
то ряд (1) сходится.
Числовые ряды
95
Доказательство:
Рассмотрим вспомогательный ряд
()()()()
11 2 2
1
nn nn
n
uu uu uu uu
∞
=
+
=+ ++ +++ +
∑
……
(3)
для него справедливо неравенство
,20
nnn
uuu ≤+≤
.,2,1 …=n
Ряд
(
∑
∞
=1
2
n
n
u
)
сходится из условия сходимости ряда (2);
Ряд (3) сходится на основании первого признака сравнения.
Ряд (1) есть разность двух сходящихся рядов
()
∑∑ ∑
∞
=
∞
=
∞
=
−+=
11 1nn n
nnnn
uuuu
и, следовательно, сходится.
Обратное утверждение неверно.
!
Сходящийся ряд, для которого ряд, составленный из абсолютных
величин его членов, также сходится, называется
абсолютно схо-
дящимся.
О
Заметим, что доказанный признак сходимости
достаточен, но не
необходим
: существуют знакопеременные ряды, для которых ряды, со-
ставленные из абсолютных величин их членов, расходятся.
Сходящийся ряд, для которого ряд из абсолютных величин его
членов расходится, называется
условно сходящимся.
О
Пример:
1. Знакочередующийся ряд
()
(
)
11
1
11
11
1
23
nn
n
...
nn
−−
∞
=
−−
=− + − + +
∑
…
сходится условно по
признаку Лейбница (см. ниже), так как
nn
1
1
1
>
−
и
,0
1
lim =
∞→
n
n
но со-
ответствующий ряд из абсолютных величин членов данного ряда
(1) является гармоническим
∑
∞
=1
1
n
n
и расходится.
2. Ряд
()
∑
∞
=
−
++−=
−
1
222
1
3
1
2
1
1
1
n
n
n
… сходится абсолютно, так как этот
знакочередующийся ряд сходится по признаку Лейбница (см. ни-
же), и ряд
∑
∞
=1
2
1
n
n
сходится тоже.

Лекции 10 - 11
96
11.3. Знакочередующиеся ряды. Признак Лейбница
Ряд называется знакочередующимся, если его члены являются (по-
очередно) положительными и отрицательными.
Такой ряд можно записать в виде
О
() ()
11
123
11
nn
n
uuuu u
−
−=−+−+−+……
1
n
n
∞
−
=
∑
..
, (1)
где
для любого . Если первый член ряда отрицателен, то
исследуют ряд
.
0
n
u >
n
()
1
1
1
n
n
n
u
∞
−
=
−−
∑
Признак Лейбница. Если в знакочередующемся ряде (1):
Т
1) абсолютные величины членов ряда монотонно убывают
,
123
uuu.>>>
2)
то а) ряд (1) сходится; б) его сумма 0 положитель-
на и не превосходит первого члена ряда, то есть,
.
,0lim =
∞→n
n
u
S >
1
Su<
Доказательство:
Рассмотрим последовательность четных частичных сумм знакоче-
редующегося ряда (1):
(
)
(
)
,,
43214212
…uuuuSuuS
−
+
−
=
−=
(
)
(
)
(
)
21234212nn
Suuuuu u
−
=−+−+ −
n
.
Каждая из разностей, стоящих в скобках, положительна по усло-
вию теоремы, значит,
и последовательность является
возрастающей.
0
2
>
n
S
n
S
2
Если записать эту сумму в виде
(
)
(
)
2123 45 2nn
S u uu uu u
,
=
−−−−−−…
то каждая из разностей в скобках положительна и
, т.е. по-
следовательность
ограничена сверху.
2n
Su<
1,
S
2n
S
Итак, последовательность
является возрастающей и ограничена
сверху, следовательно, имеет предел
2n
S
2
lim
n
n
S
→∞
=
причем
.0
1
uS
<
<
Последовательность нечетных частичных су м
2n
S
++
-
реходя к пределу, имеем
li
м
nn
Su=+
. Пе
m lim lim
nnn
nnn
SSuS
++
→∞ →∞ →∞
1 2 21
21 2 21
=
+=,
S
следова-
тельно,
, ряд (1) сходится.
lim
n
n
S
→∞
=
Признак Лейбница используется для приближенного вычисления
суммы знакочередующегося ряда с определенной точностью. Сумма

Числовые ряды
97
отброшенных членов знакочередующегося ряда Лейбница по абсолют-
ной величине не превосходит первый отброшенный член.
Пример:
Сколько членов ряда нужно взять,
чтобы сумму ряда
()
1
1
1
n
n
S
n
+
∞
=
−
=
∑
найти с точностью до 0,001?
Решение:
Представим сумму ряда в виде:
δ
+
=
k
SS , где
по признаку Лейбница.
∑∑
∞
+=
∞
=
==
11
,
kn
n
n
nk
uuS
δ
По условию,
,001,0
1
1
1
<
+
=
+
k
u
k
откуда нужно взять
членов ряда.
,999>k
1000
В результате изучения материала, изложенного в этих лекциях,
студент должен знать:
определения ряда, суммы ряда, частичной суммы ряда;
необходимый и достаточный признак сходимости ряда (критерий Коши);
необходимый признак сходимости ряда;
теоремы сравнения рядов с положительными членами;
достаточные признаки сходимости числовых рядов с положительными
членами: признак Даламбера, признак Коши, интегральный признак схо-
димости;
исследование знакопеременных рядов, абсолютная сходимость;
знакочередующиеся ряды, признак Лейбница.
Лекции 12 – 14
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
В лекциях 12 – 14 рассматриваются функциональные ряды и важнейшая их разно-
видность – степенные ряды. При достаточно широких предположениях относительно
функции ее можно представить как сумму некоторого функционального ряда, причем ма-
тематические операции над этим рядом (сложение, умножение, предельный переход, по-
членное дифференцирование и интегрирование) совершаются по тем же простым прави-
лам, что и одноименные операции над конечными суммами. Подобная простота примене-
ния
и легкость получения конкретных результатов обусловливает широкое применение
функциональных рядов в математике и ее приложениях.
12.1. Функциональные ряды. Основные определения
12.2 Равномерная сходимость
12.3. Признак Вейерштрасса
13.1. Степенные ряды. Основные определения
13.2. Вычисление радиуса сходимости
13.3. Свойства степенных рядов
13.4. Разложение функций в степенные ряды Тейлора и Маклорена
13.5. Разложение элементарных функций в ряды Маклорена
13.6. Применение степенных рядов
13.6.1. Вычисление значений функций
13.6.2. Вычисление интегралов, не берущихся в элементарных функциях
13.6.3. Решение дифференциальных уравнений
14.1. Ряды в комплексной области. Числовые ряды
14.2. Степенные ряды в комплексной области
12.1. Функциональные ряды. Основные определения
Пусть функция
(),
n
f
xn N
∈
определена в области
,
D
xD∈
Выражение вида
О
()
12
() () ()
nn
fx fx fx fx
1n
∞
=
=
++++……
∑
(1)
называется функциональным рядом.
Например,
1
sin sin sin sin .
2
n
xxx
x
nn
∞
=
=++++
∑
……
.
При
0
x
xD=∈
из функционального ряда (1) получается числовой
ряд
() ()
01020
1
()
n
n
fx fx f x
∞
=
=
++
∑
…
(2)
Функциональные ряды
99
Если для
0
x
D∈
числовой ряд (2) сходится, то точка
0
x
называется
точкой сходимости функционального ряда (1). Если в каждой точ-
ке
1
x
DD∈⊂
числовые ряды
()
1
n
n
f
x
∞
=
∑
сходятся, то функциональный
ряд(1) называется сходящимся в области
1
D
.
О
Совокупность всех точек сходимости образует область сходимо-
сти функционального ряда (1).
О
Рассмотрим частичные суммы функционального ряда (1):
(
)
(
)
(
)
(
)
12kk
Sx fx fx fx=+++… .
Ряд (1) сходится к функции
(
)
f
x в области сходимости, если предел
последовательности его частичных сумм
(
)
(
)
lim
k
k
Sx fx
→∞
=
.
Пример:
Найдите область сходимости ряда
∑
∞
=
+
+
+
+
+
+
=
+
1
2422
,
1
1
1
1
1
1
1
1
n
nn
xxxx
……
(
)
,x
∈
−∞ ∞
.
Если
,1<x то
,01
1
1
limlim
2
≠=
+
=
∞→∞→
n
n
n
n
x
u
ряд расходится, так как не
выполняется необходимый признак сходимости ряда; если
,
ряд
1x =±
1
111
222
n
∞
=
=++
∑
…
расходится; если
nn
x
x
x
22
1
1
1
:1 <
+
>
- беско-
нечно убывающая геометрическая прогрессия.
Сравнение со сходящимся рядом
∑
∞
=1
2
1
n
n
x
при
1>x
дает область
сходимости исследуемого ряда
(
)
(
)
,1 1,x
∈
−∞ − ∞∪
.
12.2. Равномерная сходимость
Пусть
. По определению предела это означает, что
для любого
() ()
lim
n
n
Sx fx
→∞
=
x
из области сходимости, например,
0
x
и
1
x
, выполняются
условия:
1)
()
(
)
(
)
01 0 0 0 0
:0,
n
xx D N nN Sx fx
ε
εε
=∈ ∀>∃ > ⇒ − <;
2)
(
)
(
)
(
)
11 01 1 1 1 1
,:0,
n
xx D x x N nN Sx fx
ε
εε
=∈ ≠ ∀>∃ > ⇒ − <
.
Заметим, что числа
и , вообще говоря, различны.
0
N
1
N
Лекции 12 - 14
100
Функциональный ряд, сходящийся для всех
1
x
D
∈
из области схо-
димости, называется
равномерно сходящимся в этой области, ес-
ли
0
ε
∀>
существует не зависящий от
x
номер
()
N
ε
, такой, что
при
(
)
nN
ε
> выполняется неравенство
(
)
n
Rx
ε
<
для всех
x
из об-
ласти сходимости, где
()
1
nk
kn
()
R
xf
∞
=+
x
=
−
∑
остаток ряда.
О
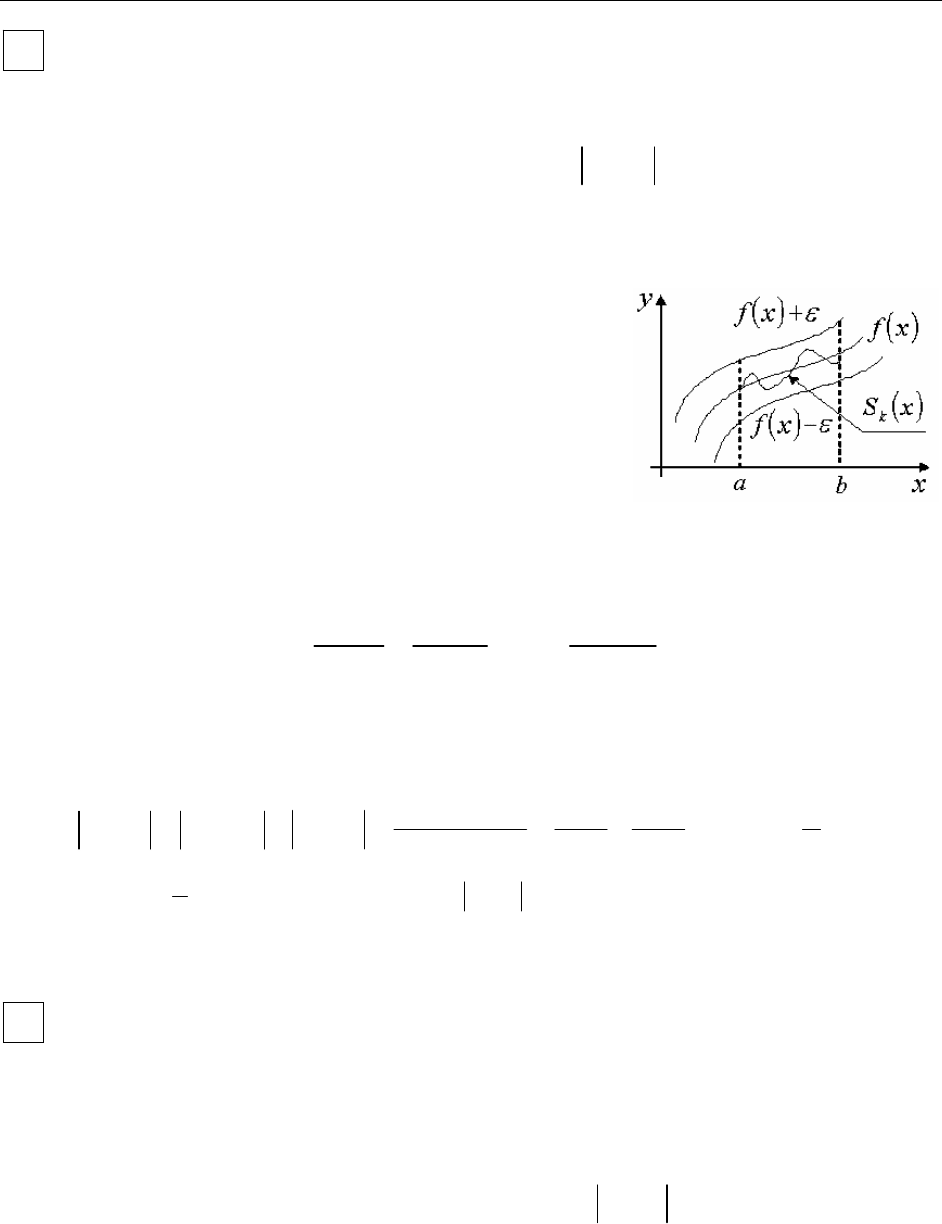
Геометрический смысл равномерной
сходимости заключается в следующем:
Если окружить график функции
(
)
yfx=
”
ε
- полоской”, определяемой соотношени-
ем
(
)
(
)
[
]
,,,
f
xyfx xab
ε
ε
−<< + ∀∈ то гра-
фики
всех функций
(
)
,
k
Sx начиная с доста-
точно большого
, целиком лежат в этой
”
k
ε
- полоске”, окружающей график предельной функции
(
)
yf= x.
Покажем, что ряд
(
)
1
24 2
1
11
12
n
n
x
xxn
+
−
−
++ +
++ +
……
сходится равно-
мерно при всех
.
()
xx−∞ < < ∞
По признаку Лейбница этот ряд сходится и его остаток можно оценить
следующим образом:
(
)
(
)
1
,
nn
R
xux
+
<
()
22
11
11
n
n
Rx
x
nn
+
<<
+
++
,
11
,1
1
n
n
ε
ε
≤
≥−
+
.
Возьмем
,1
1
−=
ε
N
тогда для
(
)
ε
<⇒≥ xRNn
n
для
x
∀
из области сходимо-
сти, значит ряд равномерно сходится.
Функциональный ряд
()
1
n
n
f
x
∞
=
∑
называется мажорируемым в неко-
торой области изменения
x, если существует такой сходящийся чи-
словой ряд
1
n
n
u
∞
=
∑
с положительными членами, что для всех x из
этой области выполняются неравенства
(
)
,1,2,
nn
fx u n≤=….
. Ряд
называется мажорантой ряда
1
n
n
u
∞
=
∑
()
1
n
n
f
x
∞
=
∑
.
О
