Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов
Подождите немного. Документ загружается.


Теория поля
81
9.3.2. Оператор Лапласа
Дифференциальные операции второго порядка возникают в результате
двукратного применения к полям оператора «набла».
Если в области G задано скалярное поле
()uuP
=
, то операция взятия
градиента порождает векторное поле:
. В векторном поле
операция взятия дивергенции порождает скалярное поле:
, а операция взятия ротора - векторное поле
.
()grad u
()ugradu∇=
()((u div grad u∇⋅∇ =
))
))((u rot grad u
⎡⎤
∇×∇ =
⎣⎦
Если в области G задано векторное поле
()aaP
=
, то операция взятия
дивергенции порождает скалярное поле:
() ( )div a a
=
∇⋅
. В скалярном поле
операция взятия градиента порождает векторное поле:
.
() ( )div a a=∇⋅
))() ((agraddiva∇∇⋅ =
Если в области G задано векторное поле
()aaP
=
, то операция взятия
ротора порождает векторное поле
()rot a
. Применяя повторно к этому полю
оператор
, получим скалярное поле
∇
(
)
(())div rot a a
⎡
⎤
=∇⋅∇×
⎣
⎦
и векторное
поле
.
(())rot rot a a
⎡⎤
⎡⎤
=∇×∇×
⎣⎦
⎣⎦
При помощи оператора Гамильтона основные понятия теории поля
можно записать в виде операций векторной алгебры.
Рассмотрим некоторые операции второго порядка.
1. Вихревое поле является соленоидальным:
(())div rot a 0
=
.
Раскроем смешанное произведение, учитывая, что векторное произведе-
ние одинаковых векторов равно нулю:
(
)
(
)
(
)
00aa a
⎡⎤
⎡⎤
∇⋅ ∇× = ⋅ ∇×∇ = ⋅ =
⎣⎦
⎣⎦
.
2. Векторное поле
является безвихревым, так как
Действительно,
()agradu=
(())rot grad u = 0.
u00uu
⎡⎤⎡⎤
∇
×∇ = ∇×∇ = ⋅ =
⎣
⎦⎣ ⎦
.
3. Рассмотрим операцию
.
((div grad u))
div grad u u=∇⋅∇(())( )
uuu
div i j k
x
yz
⎛⎞
∂∂∂
=++
⎜⎟
∂∂∂
⎝⎠
=
222
222
uuu
u
xyz
∂∂∂
+
+=∆
∂∂∂
.
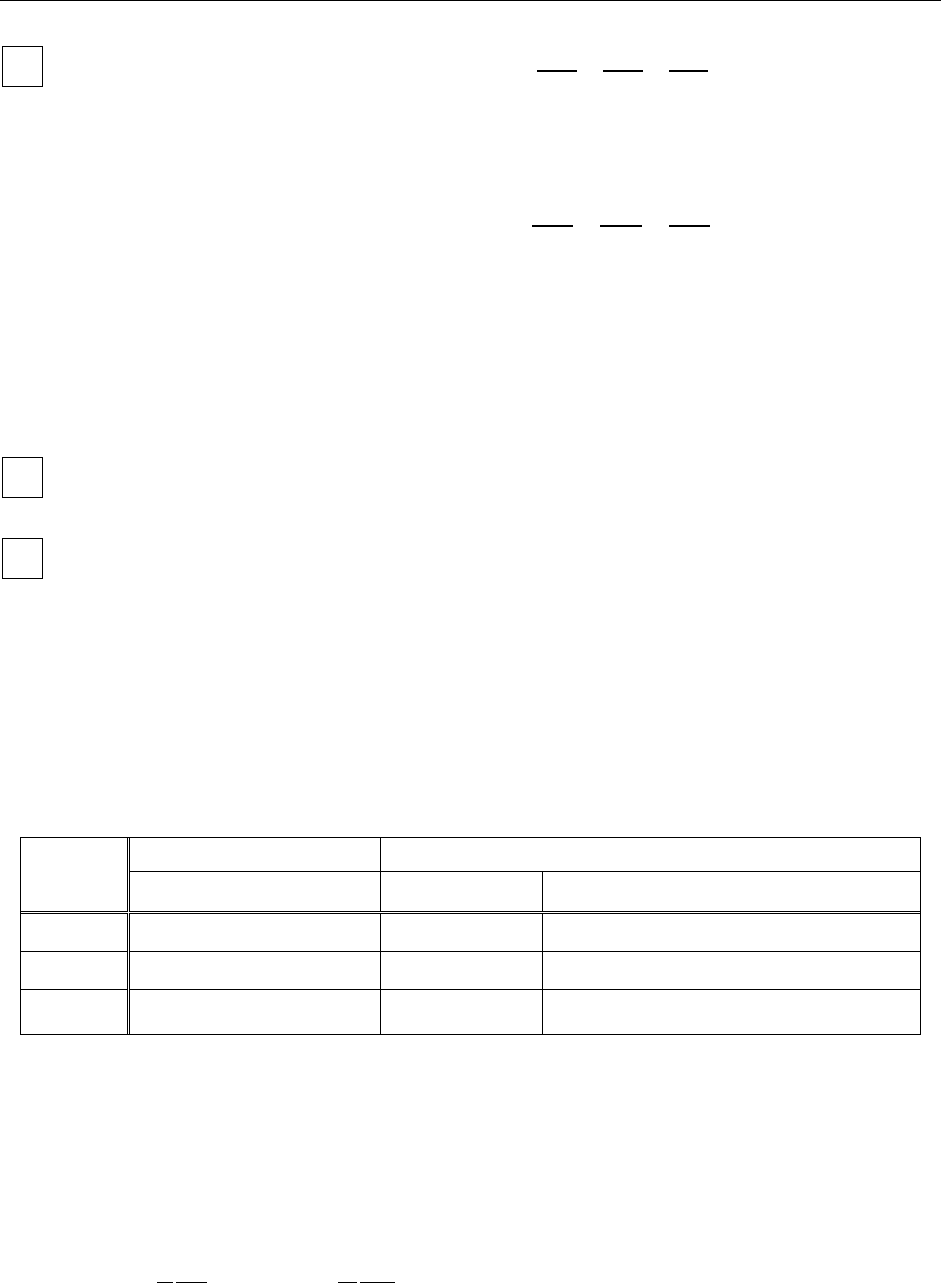
Лекция 5 - 9
82
Дифференциальный оператор вида
22
22
2
2
x
yz
∂
∂∂
∆=++
∂
∂∂
называется опера-
тором Лапласа. Оператор Лапласа можно представить как скалярное
произведение оператора Гамильтона самого на себя:
О
()∆= ∇⋅∇ =
=
222
2
222
()
x
yz
∂
∂∂
∇= + +
∂
∂∂
.
Уравнение вида
называется уравнением Лапласа и является одним из
основных уравнений математической физики. Непрерывное решение уравне-
ния Лапласа u(x, y, z) называется гармонической функцией. Соответствующее
скалярное поле называется гармоническим или лапласовым.
0u∆=
!
Векторное поле является гармоническим, если оно является одновре-
менно потенциальным и соленоидальным:
0rot a
=
; .
0div a =
Рассмотрим операцию
(()rot rot a )
.
!
Формула двойного векторного произведения дает:
{формула «бац минус цаб»}. Тогда
()(abc baccab
⎡⎤
⎡⎤
×× = ⋅− ⋅
⎣⎦
⎣⎦
)
a
⎡⎤
⎡⎤
∇× ∇× =
⎣⎦
⎣⎦
()( )aa∇∇⋅ − ∇⋅∇ =
2
()va a grad diva adi
∇
⋅−∇= −∆
.
Дифференциальные операции второго порядка удобно свести в таблицу.
Скалярное поле Векторное поле
grad
div
rot
grad
()grad diva
div
(())div grad u u=∆
(())div rot a 0
=
rot
(())rot grad u = 0
(())rot rot a
=
()
g
rad diva a−∆
Как пример применения дифференциальных операций второго порядка,
можно рассмотреть уравнения Максвелла, описывающие электромагнитное
поле в дифференциальной форме:
[]
E
H
ct
ε
∂
=∇×
∂
;
[]
H
E
ct
µ
∂
−=∇×
∂
;
()0E
∇
⋅=
;
()0H
∇
⋅=
.
Иначе:
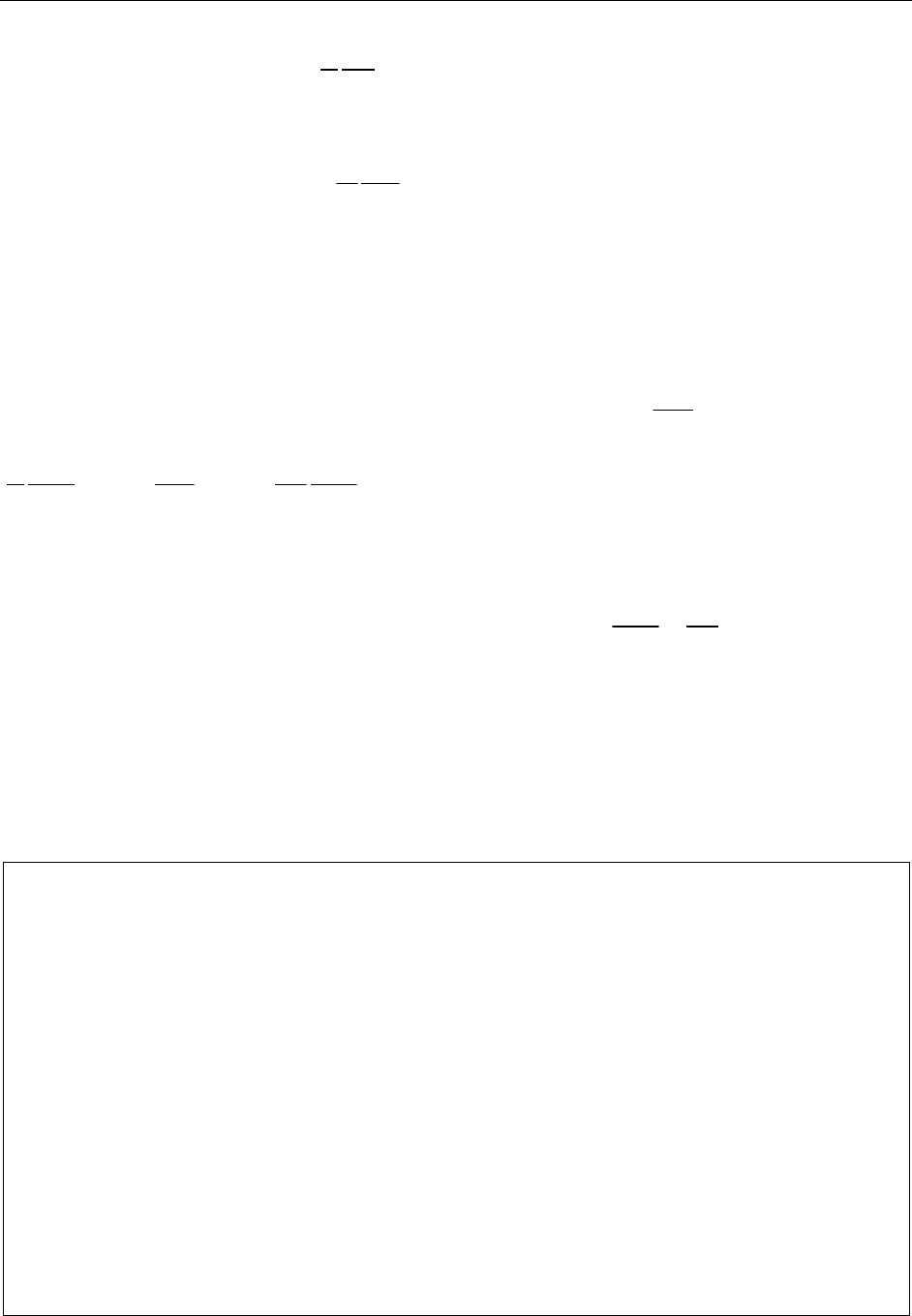
Теория поля
83
,(
0, (2)
,(
0. (4)
E
rotH
ct
divE
H
rotE
ct
divH
ε
µ
⎧
∂
=
⎪
∂
⎪
=
⎪
⎨
∂
⎪
−=
⎪
∂
⎪
=
⎩
1)
3)
В этих уравнениях , - векторы напряжённости электрического и
магнитного полей;
E
H
ε
,
µ
- электрическая и магнитная проницаемости; c - ско-
рость света, зарядов и токов в данном случае нет.
Если продифференцировать (1) по
t
и подставить
H
t
∂
∂
из (3), то получим
2
2
E
H
ct t
ε
∂⎡∂
=∇×
⎢⎥
∂∂
⎣⎦
⎤
или
2
22
E
E
ct
εµ
∂
⎡
⎤
⎡
⎤
=∇×∇×
⎣
⎦
⎣
⎦
∂
. Преобразуем правую часть по
формуле:
()
E
E Е
⎡⎤
⎡⎤
∇× ∇× =∇ ∇⋅ −∆
⎣⎦
⎣⎦
.
Итак, для векторного поля
E
имеем уравнение
22
2
Е c
E
t
εµ
∂
=
⋅∆
∂
.
Это одно из основных уравнений математической физики, называемое
вол-
новым уравнением.
В результате изучения материала, изложенного в этих лекциях,
студент должен владеть следующими понятиями и уметь вычислять:
скалярное и векторное поля, способы наглядного описания
(поверхности и линии уровня, векторные линии);
интегральные характеристики векторного поля:
поток, способы его вычисления, физический смысл;
линейный интеграл, способы вычисления, физический смысл;
дифференциальные характеристики скалярного и векторного полей:
градиент, его свойства и способы вычисления;
дивергенция, ее свойства и способы вычисления;
ротор, его свойства и способы вычисления;
связь между дифференциальными и интегральными характеристиками
(теорема Остроградского – Гаусса, теорема Стокса);
инвариантные определения дифференциальных характеристик;
специальные виды векторных полей, их свойства;
операторы Гамильтона и Лапласа.
Лекции 10 - 11
ЧИСЛОВЫЕ РЯДЫ
В лекциях 10 – 11 рассматриваются числовые ряды – важнейшее средство изображе-
ния, изучения и приближенного вычисления чисел и функций. Приведены основные по-
ложения, позволяющие исследовать вопрос о сходимости ряда и, в отдельных случаях,
приближенно вычислять значение суммы ряда.
10.1. Числовые ряды. Общие положения
10.2. Ряды с положительными членами
10.3. Теоремы сравнения рядов c положительными числами
11.1. Достаточные признаки сходимости числовых рядов
с положительными членами
11.1.1. Признак Даламбера
11.1.2. Признак Коши
11.1.3. Интегральный признак сходимости
11.2. Знакопеременные ряды
11.3. Знакочередующиеся ряды. Признак Лейбница
10.1. Числовые ряды. Общие положения
Выражение
, где
12
1
n
n
uuu u
∞
=
=++++
∑
…
n
…
{
}
n
u - заданная бесконеч-
ная числовая последовательность, называется числовым рядом, а
числа
- членами ряда.
n
u
Конечные суммы ,
11
Su=
21
Suu
2
=
+
,...,
12n
Suu
n
u
=
+++… называются
частичными суммами ряда.
Если существует конечный предел последовательности частичных
сумм
, то ряд называется сходящимся, а число S - суммой
ряда. В противном случае
n
n
SS
∞→
= lim
(
)
,
n
SS→∞∃
ряд расходится и суммы не
имеет.
Пример:
Исследуйте на сходимость ряд:
∑
∞
=
+
1
)1(
1
n
nn
.
Частичная сумма
)1(
1
32
1
21
1
+
++
⋅
+
⋅
=
nn
S
n
… .
Разложим
)1(
1
+nn
на сумму простейших дробей:
1
11
)1(
1
+
−=
+ nnnn
,
О
О
О
Числовые ряды
85
тогда
1
1
2
n
S =−
1
2
+
1
3
−
1
3
+
1
...
n
++
11
1
11nn
−=−
+
+
,
, ряд сходится по определению.
1lim =
∞→
n
n
S
Пример:
1.
, ряд расходится.
∞=
∑
∞
=1n
n
2.
…−+−+−=−
∑
∞
=
1111)1(
1n
n
1234
1, 0, 1, 0,SSSS
=
−= =−=…
Предел частичных сумм не существует, ряд расходится.
3.
По формуле суммы геометрической про-
грессии
12
1
1
n
n
qqq
∞
−
=
=+ + +
∑
…
()
1
1
1
n
n
bq
S
q
−
=
−
, для
1
1
=
b
получаем
q
q
S
n
n
−
−
=
1
1
.
1). Если
,1<q
то и
0
n
n
q
→∞
⎯⎯⎯→
S
q
S
n
n
=
−
=
∞→
1
1
lim .
2). Если
,1>q
то,
n
n
q
→∞
⎯⎯⎯→∞
⇒
∞
→
n
S предел не существу-
ет.
n
S
3). Если
, то
1q =
n
Sn
=
,
∞
=
∞→
n
n
Slim
.
Если
1q
=
−
, то
и предел не существует.
Итак,
⎢
⎣
⎡
=
нечетномпри
четномпри
n
S
n
,1
,,0 n
⎢
⎢
⎣
⎡
≥
<
∑
∞
=
−
.1
;1
1
1
q
q
q
n
n
прирасходится
присходится
Отбрасывание конечного числа начальных членов ряда не влияет
на его сходимость (но влияет на сумму).
Т
Доказательство:
Рассмотрим ряды:
(1)
…… ++++=
∑
∞
=
n
n
n
uuuu
21
1
…++=
++
∞
+=
∑
21
1
mm
mn
n
uuu
(2)
Обозначим сумму отброшенных членов через А. Тогда частичная
сумма для ряда (1) при n>m равна
mnn
AS
−
+
=
δ
, где
mn−
δ
- частич-
ная сумма ряда (2).
Лекции 10 - 11
86
При
:
∞→n
∞
→=− kmn )(
,
.limlim
k
k
n
n
AS
δ
∞→∞→
+
=
Так как существу-
ет
lim
n
A
A , то
n
S и
k
→∞
=
δ
сходятся или расходятся одновременно (по
теореме о пределе суммы).
Если члены сходящегося ряда
1
n
n
u
∞
=
S
=
∑
умножить на одно и то же
число
С, то его сходимость не нарушится, а сумма умножится на
это число:
.
1
n
n
Cu CS
∞
=
=
∑
Т
Доказательство: lim lim
nn
nn
CS C S CS
→∞ →∞
=
= .
Пример:
Ряд сходится при
1
1
n
n
aq
∞
−
=
∑
.1<q
.
,
11
n
n
aaq a
SS
qq
⎛⎞
−
==
⎜⎟
−−
⎝⎠
Два сходящихся ряда
и можно почленно склады-
вать (вычитать) так, что ряд
- сходится, и его сумма
равна
Aa
n
n
=
∑
∞
=1
Bb
n
n
=
∑
∞
=1
∑
∞
=
±
1
)(
n
nn
ba
B
A
±
.
Т
Доказательство:
11 2 2
()( ) ( )
nn
Sabab ab=±+±++±=…
n
=
;
12 12
()()
nn
aa bb AB++ + ++ = ±……
.limlimlim BABAS
n
n
n
n
n
n
±
=
±
=
∞→∞→∞→
Критерий Коши сходимости числового ряда. Для того чтобы число-
вой ряд был сходящимся, необходимо и достаточно, чтобы для
()
NnNN >∀=∃>∀ ,,0
ε
ε
и k = 1,2,3,… выполнялось неравенство
ε
<
+
++=−
++++ knnnnkn
uuuSS …
21
.
Т
Числовые ряды
87
Т
Необходимый признак сходимости числового ряда.
Если ряд
сходится, то общий член сходящегося ряда стремится к нулю
при
,
∑
∞
=1
n
n
u
∞→
n
.0lim =
∞→
n
n
u
Доказательство:
.1−
−=
nnn
SSu
Так как
,limlim
1
SSS
n
n
n
n
=
=
−
∞→∞→
то
.0lim
=
∞→
n
n
u
В противном
случае ряд расходится.
Это условие не является достаточным.
Покажем, что гармонический ряд
∑
∞
=
+++++=
1
1
3
1
2
1
1
1
n
nn
…… расхо-
дится, несмотря на то, что
.0
1
limlim ==
∞→∞→
n
u
n
n
n
Рассмотрим
2
11 111 1 1
1 2 222 2 22
nn
SS n
nn nnn n n
−= + ++>+++=⋅=
++
……
1
.
Таким образом, критерий Коши не выполняется и гармонический
ряд
∑
∞
=1
1
n
n
расходится.
Пример:
1. Исследуйте на сходимость ряд
2
1
n
Ряд расходится, так как для него не выполняется необходимый
признак сходимости:
45
.
(1)( 2)
n
nn
∞
=
−
−+
∑
22
2
45 45
lim lim lim 5 0
(1)( 2) 2
n
nn n
nn
u
nn nn
→∞ →∞ →∞
−−
==
−+ +−
=−≠
2. Исследуйте на сходимость ряд
∑
∞
=
⎟
⎠
⎞
⎜
⎝
⎛
+
1
.
1
n
n
n
n
Проверим выполнение необходимого признака сходимости:
11
0
11
1
n
nn
nn n
lim u lim lim
e
n
nn
→∞ →∞ →∞
===
+
⎛⎞ ⎛⎞
+
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
1
≠
;
ряд расходится.
Лекции 10 - 11
88
10.2. Ряды с положительными членами
Рассмотрим числовой ряд где
. Для такого ряда
12
1
,
nn
n
uuu u
∞
=
=++++
∑
……
n
,0≥
n
u
123n,,,= …
11
,
nnn
SSuS
++
=
+≥
значит, последователь-
ность частичных сумм возрастает. Из теоремы о пределе монотонной
последовательности вытекает следующее.
Условие сходимости ряда с положительными членами: ряд с по-
ложительными членами всегда имеет сумму; она будет
конечна (ряд
сходящимся), если частичные суммы ряда ограничены сверху, и бес-
конечна
(ряд расходящимся) в противном случае.
10.3. Теоремы сравнения рядов с положительными членами
Пусть даны два положительных ряда:
1
n
n
u
∞
=
∑
, (1)
0
n
u ≥
и
1
n
v
∞
=
∑
n
v ≥
n
,
n
. (2)
0
Т
Если хотя бы начиная с некоторого
n выполняется неравенство
, то из сходимости ряда (2) следует сходимость ряда (1); из
расходимости ряда (1) следует расходимость ряда (2).
n
uv≤
Доказательство:
Так как отбрасывание конечного числа начальных членов ряда не
влияет на сходимость, можно считать, что
nn
vu
≤
.
1, 2, 3,n∀= …
Для частичных сумм этих рядов выполняется
.
nn
UV
≤
Пусть ряд
сходится, тогда
V
∑
∞
=1n
n
v
,S
n
≤
откуда
n
US
≤
и ряд схо-
дится.
∑
∞
=1
n
n
u
Пусть
расходится, тогда
U
,
V
и ряд расходится.
∑
∞
=1
n
n
u
S
n
≥
n
≥ S
∑
∞
=1
n
n
v
Т
Если существует конечный предел отношения общих членов (1) и
(2)
k
v
u
n
n
n
=
∞→
lim
,
,0≠
n
v
,0
∞
<
≤
k
то оба ряда либо одновременно
сходятся, либо одновременно расходятся.

Числовые ряды
89
Пример:
Исследуйте на сходимость следующие ряды:
1)
…… +++++=
∑
∞
=1
1
3
1
2
1
1
1
n
nn
Сравним члены этого ряда с членами расходящегося гармониче-
ского ряда
1
1
.
n
n
∞
=
∑
. Так как
n
n
11
≥
,исследуемый ряд расходится.
2) Ряд
∑
∞
=1
2
1
n
n
сходится по теореме сравнения, так как предел отно-
шения общего члена данного ряда к общему члену сходящегося
(доказано ранее) ряда
()
∑
∞
=
+
1
1
1
n
nn
есть
1
)1(
)1(
lim
2
=
+
+
∞→
n
nn
n
, постоянное
число.
3)
∑
∞
=
+++++=
1
32
1
3
1
2
1
1
1
n
nn
nn
………
.
Сравним этот ряд с рядом
…… ++++=
∑
∞
=
n
n
n
2
1
2
1
2
1
2
1
2
1
32
1
, который
представляет собой бесконечно убывающую геометрическую про-
грессию со знаменателем
1
2
1
<=q
, а следовательно, сходится.
Так как
,
2
11
nn
n
<
исследуемый ряд сходится.
4) Ряд
∑∑
∞
=
∞
=
=
⎟
⎠
⎞
⎜
⎝
⎛
+
11
1
1ln
nn
n
u
n
.
Сравним этот ряд с расходящимся рядом
11
1
n
nn
v
n
∞
∞
==
=
∑
∑
:
()
1lim
1ln
limlim
1
1
1
1
==
+
=
∞→∞→∞→
n
n
n
n
n
n
n
n
n
v
u
, с учетом того, что
)~)1(ln(
α
α
+
,
0
α
→
.
Приведем полученные данные о сходимости некоторых рядов, ко-
торые могут быть использованы для сравнения:
1.
1
сходится, если 1,
1
р
асходится, если 1.
n
n
α
α
α
∞
=
>
⎡
⎢
≤
⎣
∑
2.
1
сходится, если 1,
расходится, если 1.
n
n
a
a
a
n
∞
=
<
⎡
⎢
≥
⎣
∑
3.
1
1
сходится.
(1)
n
nn
∞
=
+
∑
4.
0
сходится при 1,
расходится при 1.
1
n
n
q
a
aq
q
q
∞
=
⎡
<
=
⎢
≥
−
⎣
∑
Лекции 10 - 11
90
11.1. Достаточные признаки сходимости числовых рядов
с положительными членами
11.1.1. Признак Даламбера
Рассмотрим ряд с положительными членами и предел отно-
шения последующего члена ряда к предыдущему.
1
n
n
u
∞
=
∑
1) Если
и 2) существует
0;
n
u >
1
lim ,
n
n
n
u
l
u
+
→∞
=
тогда
1
сходится, если 1,
расходится, если 1,
признак не дает ответа, если 1.
n
n
l
ul
l
∞
=
<
⎡
⎢
>
⎢
⎢
=
⎣
∑
Доказательство:
,:0lim
1
NnNl
u
u
n
n
n
≥∃>∀⇒=
+
∞→
ε
,
1
ε
<−
+
l
u
u
n
n
т.е. .
1
εε
+<<−
+
l
u
u
l
n
n
Рассмотрим 3 случая:
1)
1.l <
Выберем
ε
столь малым, чтобы
1,l
ε
+
<
тогда, полагая ,lq
ε
+=
имеем
0
q<<
1,
1
,
n
n
u
q
u
+
<
1nn
uu
+
q
<
⋅
для
1
,1,2,,
NN
nNN N u uq
+
,
=
++ <⋅…
и т.д.
2
21
,
NN N
uuquq
++
<⋅<⋅
3
32NN N
uuqu
++
<⋅<⋅q
Члены ряда
меньше членов геометрической
прогрессии:
Так как
123
(1)
NN N
uuu
++ +
+++…
23
(2).
NN N
uq uq uq+++…
,1
<
q
то ряд (2) сходится,
значит, по теореме сравнения сходится и ряд (1).
2)
1.l >
Возьмем
0>
ε
столь малым, что
,1>
−
ε
l
тогда при nN≥
1
1,
n
n
u
u
+
>
члены ряда не стремятся к нулю, т.е. не выполняется необхо-
димый признак сходимости ряда, следовательно, ряд расходится.
1
,
n
uu
+
>
n
3)
1.l =
Покажем, что в этом случае ряд может как сходиться, так и расхо-
диться.
1).
Гармонический ряд
∑
∞
=1
1
n
n
расходится, для него
1
lim lim 1.
1
n
nn
n
un
un
+
→∞ →∞
==
+
