Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов
Подождите немного. Документ загружается.

Функциональные ряды
101
12.3. Признак Вейерштрасса
(признак равномерной сходимости функционального ряда)
Функциональный ряд
сходится равномерно в области сходимости,
если он является
мажорируемым в этой области.
Например, для рядов
в силу ограни-
ченности функций выполняется
() ( )
11
sin 1 cos 2
nn
nn
anx, , a nx
∞∞
==
∑∑
sin ,
nn
anxa
≤
cos .
nn
anxa
≤
По признаку Вейерштрасса, если ряд
1
n
n
a
∞
=
∑
сходится абсолютно, то ря-
ды (1), (2) сходятся
равномерно на
∀
промежутке.
Теоремы о почленном интегрировании и дифференцировании
функциональных рядов
Пусть ряд
() ()
1
n
n
f
xfx
∞
=
=
∑
с непрерывно дифференцируемыми чле-
нами сходится для
[]
,
x
ab∈ и ряд
()
n
1n
f
x
∞
=
′
∑
сходится равномерно на
[
]
,ab
, тогда
(
)
n
f
x
∑
сходится равномерно, его сумма дифферен-
цируема и
() ()
1
,
n
n
f
xfx
∞
=
′
′
=⎡⎤
⎣⎦
∑
т.е. ряд
()
n
1n
f
x
∞
=
∑
n
можно дифферен-
цировать
почленно.
Пусть ряд
1n
() ()
f
xfx
∞
=
=
∑
равномерно сходится на
[
]
,ab, тогда:
1) этот ряд можно почленно интегрировать на этом отрезке и
2) ряд
() ()
1
bb
n
n
aa
f
xdx f xdx
∞
=
=
∑
∫∫
сходится равномерно.
Пример:
Найдите сумму ряда .
()
()
∑
∞
=
+
=++
0
12
59
n
n
xfxnn
Решение:
Для нахождения суммы ряда воспользуемся известной формулой
для суммы геометрической прогрессии
2
0n
=
Дифференцируя левую и правую части формулы (1), получим по-
1
1,1
1
n
xxx x
x
∞
=+ + + = <
−
∑
…
. (1)
Т
Т
Лекции 12 - 14
102
следовательно,
1
1
1
1
n
n
nx
x
∞
−
=
′
⎛⎞
=
⎜⎟
−
⎝⎠
∑
,
()
2
2
1
1
1
n
n
nn x
x
∞
−
=
″
⎛
−=
⎜
−
⎝⎠
∑
⎞
⎟
. (2)
Заменим в формулах (2) индекс суммирования:
()
,1
1
1
0
∑
∞
=
+=
′
⎟
⎠
⎞
⎜
⎝
⎛
−
n
n
xn
x
()()
.12
1
1
0
∑
∞
=
++=
″
⎟
⎠
⎞
⎜
⎝
⎛
−
n
n
xnn
x
Выделим в сумме, подлежащей вычислению, слагаемые, пропор-
циональные первой и второй производной:
()
( )()()
()
21
00
95 2 16 13
nn
nn
nnx n n n x
∞∞
++
==
+ + = + ++ +− =
∑∑
1
0
n
n
∞
=
=
∑
( )() ()
00
216 13
nn
nn
x n nx nx x
∞∞
==
⎛⎞
= +++ +−
⎜⎟
⎝⎠
∑∑
111
63
111
x
xx
⎛⎞
′′ ′
⎛⎞⎛⎞⎛⎞
⎜⎟
=+−
⎜⎟⎜⎟⎜⎟
⎜⎟
−−−
⎝⎠⎝⎠⎝⎠
⎝⎠
x
.
Вычислим производные:
()
()
()
22
111 1 2
11
11
,,
xx
3
1
x
xx
′
′″
⎛⎞
⎛⎞ ⎛⎞
⎜⎟
===
⎜⎟ ⎜⎟
⎜⎟
−−
⎝⎠ ⎝⎠
−−
⎝⎠
−
тогда
()
()
()
()
3
32
2633
1
11 1
x
3
5
f
xx
x
xx x
⎧⎫
.
−
+
⎪⎪
=+−=
⎨⎬
−
−− −
⎪⎪
⎩⎭
13.1. Степенные ряды. Основные определения
Функциональный ряд вида
О
() ()()
…+−+−+=−
2
020100
xxaxxaaxx
n
n
∑
∞
=
0
a
n
(1)
называется
степенным по степеням
(
)
0
x
x
−
.
В частности, при
ряд
0
0x =
…+++=
∑
∞
=
2
210
0
xaxaaxa
n
n
n
(2)
является степенным по степеням
x.
Ряд (1) сводится к ряду (2) заменой
(
)
0
x
xx
−
→ , - коэффици-
енты ряда. Ряд (2) сходится по крайней мере в одной точке: при
012
,,aaa…
0
0
x
Sa==
.
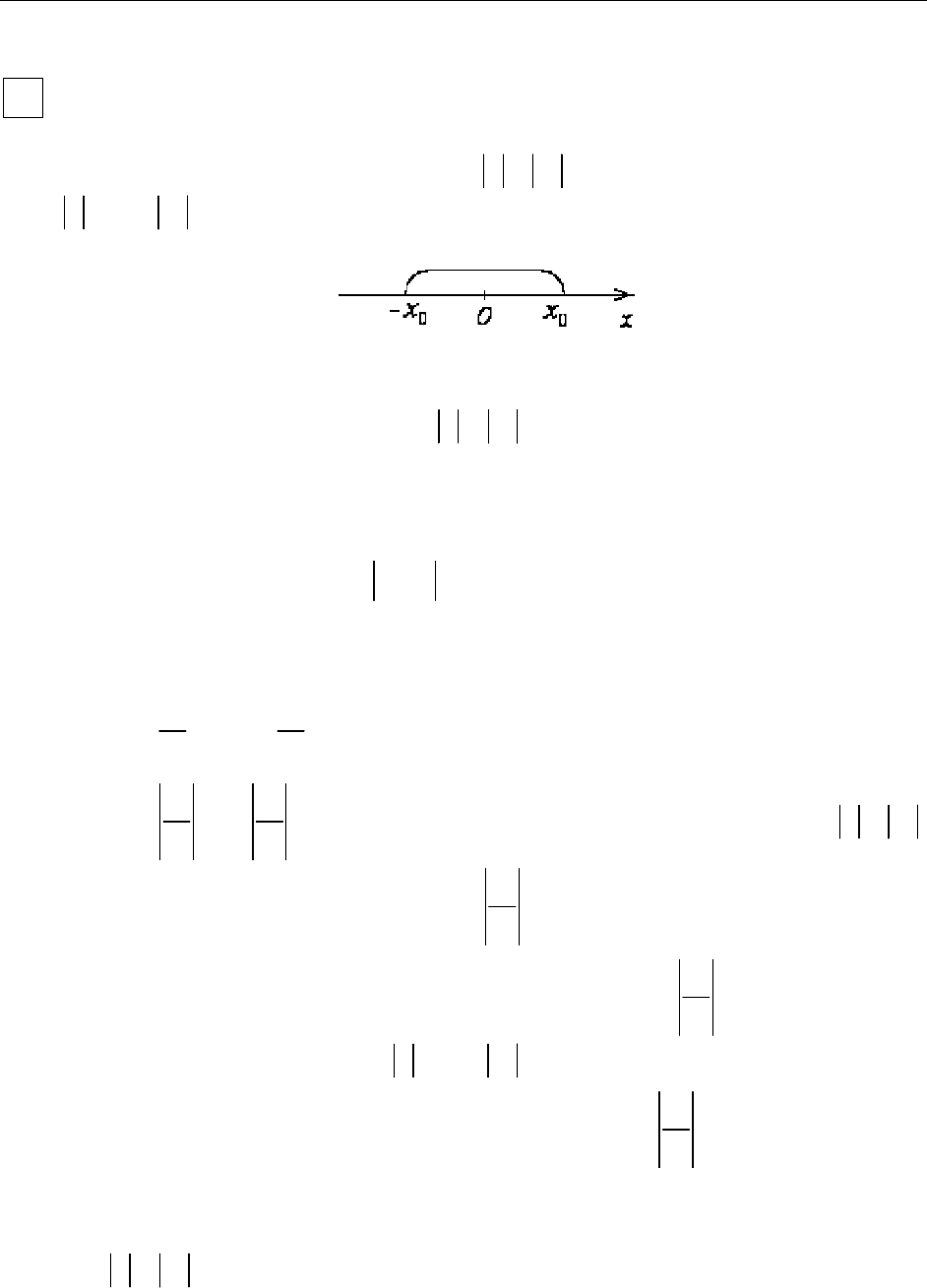
Функциональные ряды
103
Область сходимости степенного ряда. Теорема Абеля
1) Если степенной ряд сходится в точке , то он
абсолютно сходится для
0
n
n
n
ax
∞
=
∑
(
0
00
≠xx
)
0
:
x
xx
∀
< , причем на отрезке
∀
0
x
Rx≤< сходимость будет равномерной.
Т
2) Если степенной ряд расходится в точке
(
)
00
0xx
′
′
≠
, то он расхо-
дится и для всех
x таких, что
0
x
x
′
> .
Доказательство:
1) Пусть
сходится, тогда
0
0
n
n
n
ax
∞
=
∑
0
lim 0
n
n
n
ax
→∞
=
⇒ последовательность
ограничена
0
n
n
ax
0
:
n
n
M
ax M⇔∃ < .
Рассмотрим ряд
, запишем его в виде:
0
n
n
n
ax
∞
=
∑
2
2
010 20
00
xx
aax ax
xx
⎛⎞
++ +
⎜⎟
⎝⎠
… и сравним с рядом
2
00
xx
MM M
xx
+⋅ + +…, который представляет собой при
0
x
x
<
геометрическую прогрессию
0
1
x
g
x
=
<
, т.е. сходится, следователь-
но, ряд
абсолютно сходится, т.к.
0
n
n
n
ax
∞
=
∑
0
n
n
n
x
ax M
x
≤ .
При этом на
∀
отрезке
0
x
Rx
≤
< сходимость равномерная, т.к.
сходится
мажорирующий числовой ряд
0
0
n
n
R
M
x
∞
=
⋅
∑
.
2) Пусть ряд
расходится. Докажем, что он расходится при
()
0
0
n
n
n
ax
∞
=
′
∑
0
:
x
xx
′
∀>.
Лекции 12 - 14
104
От противного: пусть
0
:
x
xx
′
∃>
и ряд сходится, следова-
тельно, по 1-ой части теоремы Абеля ряд бы сходился в точке
0
n
n
n
ax
∞
=
∑
(
)
00
..
x
тк xx
′′
<
, что противоречит условию.
1). Областью сходимости степенного ряда является симметричный
интервал с центром в точке О.
С
2). Существует граница между точками сходимости
0
x
и расходи-
мости
0
x
′
:
{
}
{
}
00
inf
R
Sup x x
′
==.
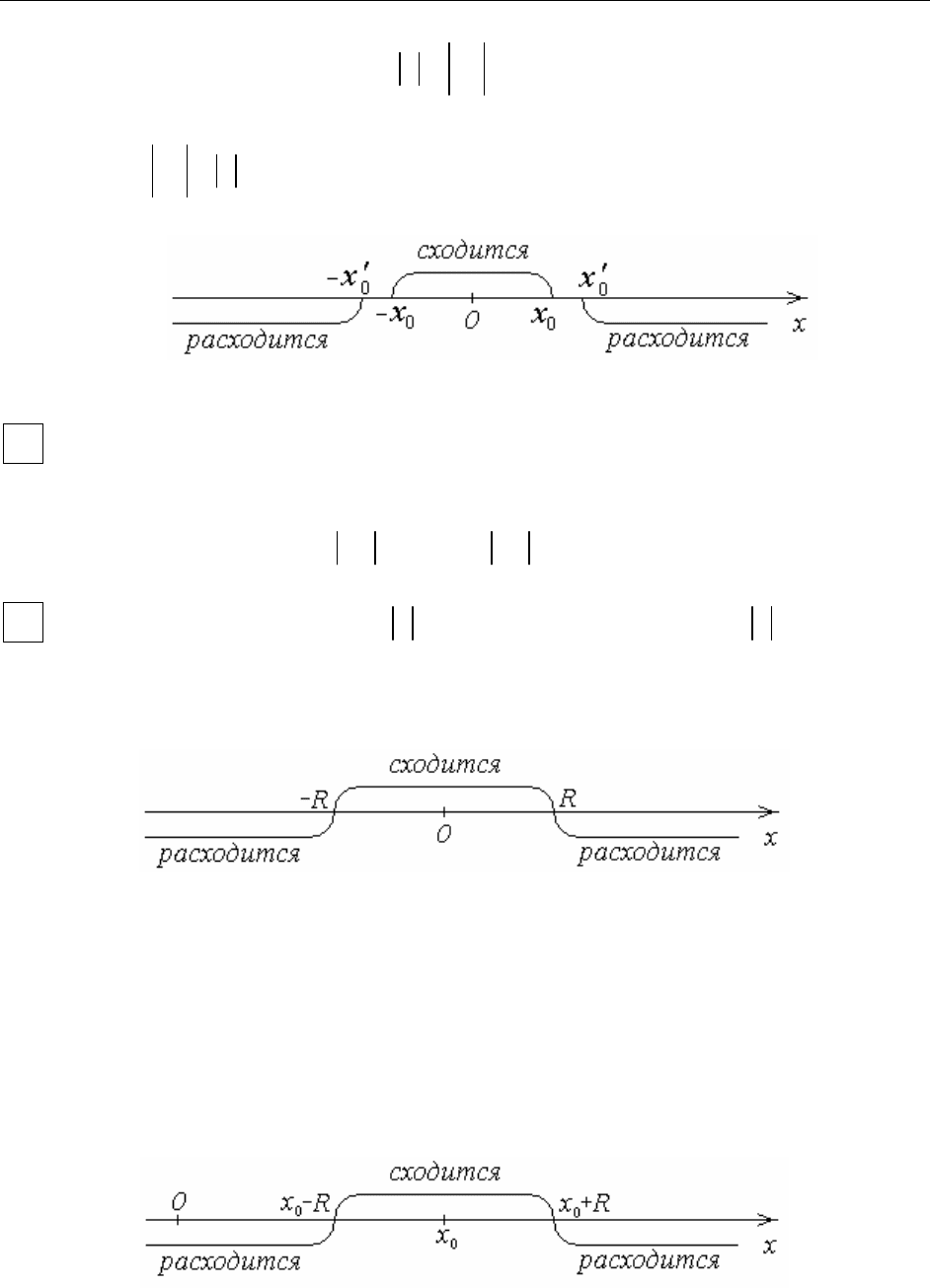
О
Число
R
такое, что при
x
R
<
ряд сходится, а при
x
R> - расхо-
дится, называется
радиусом сходимости степенного ряда, а интер-
вал
(
)
,
x
RR∈− - интервалом сходимости.
В граничных точках
x
R
=
± поведение ряда требует дополнитель-
ного исследования.
Для ряда
интервал сходимости имеет вид:
(
0
0
n
n
n
axx
∞
=
−
∑
)
(
)
00
,
x
xRxR
∈
−+
с центром в точке
0
:
x

Функциональные ряды
105
13.2. Вычисление радиуса сходимости
Степенные ряды в области сходимости сходятся абсолютно и мож-
но использовать признаки сходимости рядов с положительными члена-
ми.
1.
По признаку Даламбера:
(
)
()
1
1
1
1
lim lim lim
n
n
n
n
n
nn n
nn
n
ax
ux
a
x
ux a
ax
+
+
+
+
→∞ →∞ →∞
==
1, сходится,
1, расходится.
<
⎧
⎨
>
⎩
Ряд сходится, если
1
1
lim
n
n
n
x
a
a
+
→∞
<
.
1
1
1
lim .
lim
n
n
n
n
n
n
a
R
a
a
a
→∞
+
+
→∞
==
2.
По признаку Коши:
()
lim lim lim
n
n
n
n
nn n
nn n
ux ax x a
→∞ →∞ →∞
==⋅
1, сходится,
1, расходится.
<
⎧
⎨
>
⎩
Ряд сходится, если
1
lim
n
n
n
x
a
→∞
<
.
1
lim
n
n
n
R
a
→∞
=
Пример:
Найдите область сходимости рядов: 1)
∑
∞
=1n
n
n
x
и 2)
∑
∞
=1
!
n
n
n
x
.
1)
.1
1
limlim
lim
1
1
1
=
+
===
∞→
+
∞→
+
∞→
n
n
a
a
a
a
R
n
n
n
n
n
n
n
Интервал сходимости
(
)
.1,1
−
∈
x
.
Исследуем граничные точки.
∑
∞
=
−⇒=
1
1
1
n
n
x
расходится;
(
)
1
1
1
n
n
x
n
∞
=
−
=− ⇒
∑
- сходится условно по признаку Лейбница.
Область сходимости ряда
[
)
1,1
−
∈
x
.
2)
()
()
∞=+=
+
=
∞→∞→
1lim
!
!1
lim n
n
n
R
nn
, ряд сходится при всех .
()
∞∞−∈ ,x

Лекции 12 - 14
106
13.3. Свойства степенных рядов
В силу теоремы Абеля степенной ряд сходится
равномерно на
(
)
,
R
R− , его можно почленно дифференцировать и интегрировать в ин-
тервале сходимости.
Ряды, полученные почленным дифференцированием и интегриро-
ванием степенного ряда, имеют тот же интервал сходимости и их
сумма внутри интервала сходимости равна соответственно произ-
водной и интегралу от суммы первоначального ряда.
Т
Пример:
1) сходится равномерно при , удов-
летворяющих неравенству
23
1
n
n
xxxx
∞
=
=+ + +
∑
…
x∀
1x
<
,
1
1
n
n
x
x
x
∞
=
=
−
∑
– сумма бесконечно убывающей геометрической
прогрессии.
Этот ряд можно почленно интегрировать и дифференцировать:
1
2
1
1
11
n
n
x
nx ;
x
x
∞
−
=
′
−
⎛⎞
==
⎜⎟
−−
⎝⎠
∑
()
1
1
0
ln 1 .
11
x
n
n
xt
dt x x
nt
+
∞
=
==−−−
+−
∑
∫
2)
()
0
n
n
n
ax f x .
∞
=
=
∑
()
(
)
22
01 2 1 2 3
;23fx a ax ax f x a ax ax
′
=+ + + =+ + +……,
()
2
1
0
.
2
ax
fxdx c ax=+ + +
∫
…
13.4. Разложение функций в степенные ряды
Тейлора и Маклорена
Формула Тейлора для
(
)
:
f
x
()
()
()
()
(
)
()
(
)
(
)
()
()
2
00 0
00 0 0
12
n
n
n
fx f x f x
f
xfx xx xx xx Rx
!! n!
′′′
=+ −+ −++ −+…
,

Функциональные ряды
107
где
()
()
()
()
()
()
1
1
00
0
1
n
n
n
fx xx
Rx xx
n!
θ
+
+
+−
=
+
−
- остаточный член в форме Ла-
гранжа, где
01
θ
<<
.
Функция
()
f
x , имеющая производные всех порядков в интервале
0
x
x−<R, однозначно представима на этом интервале своим рядом
Тейлора
:
() ( )
0
0
n
n
n
f
xaxx
∞
=
=−
∑
, где
(
)
(
)
0
!
n
n
f
x
a
n
=
, тогда и только тогда,
когда
(
)
lim 0
n
n
Rx
→∞
=
.
Т
Доказательство:
По формуле Тейлора
()
(
)
(
)
nn
f
xPxRx
=
+ ,
()
()
(
)
()
(
)
(
)
()
00
00
.
1! !
n
n
n
fx f x
Px fx xx xx
n
′
=+ −++ −…
0
Так как
(
)
lim 0
n
n
Rx
→∞
=
, то
(
)
(
)
lim
n
n
f
xP
→∞
⇒= x
.
()
n
Px - частичная сумма ряда Тейлора, ее предел равен сумме ряда
()
f
x , значит, разложение справедливо.
()
()
(
)
()
(
)
()
2
00
00
1! 2!
fx f x
fx fx x x x x
0
′
′′
=
+−+−…+
.
При
ряд
0
0x =
() ()
(
)
(
)
(
)
2
0
00 0
0
1! 2! !
n
nn
n
n
ff f
fx ax f x x x
n
∞
=
′′′
==++ ++
∑
……
+
называется
рядом Маклорена.
Для того, чтобы функцию
(
)
f
x м
n
x
=
на и
ожно было разложить в степенной
ряд
n
a
∞
∑
нтервале
0
n
(
)
,
R
R
−
достаточно, чтобы
()
f
x имела
на
(
,
)
R
R− водные всех порядков и чтобы существовала та-
кая постоянная
произ
M
, ч
()
(
то
)
n
f
x
Т
M
≤
при
0,1n ,2,
=
…
и при всех
(
)
,
x
RR . ∈−
Доказательство:
Так как
()
f
x имеет производные всех порядков, для нее можно
формально построить ряд Маклорена. Докажем, что он сходится к
Лекции 12 - 14
108
()
f
x . По теореме 1 достаточно доказать, что
(
)
0
n
n
Rx
→∞
→ для
(
)
,
x
RR∈− .
Остаточный член формулы Маклорена в форме Лагранжа можно
оценить следующим образом:
()
()
(
)
() ()
1
1
1
1! 1!
n
n
n
n
fx
M
R
Rx x
nn
θ
+
+
+
=<
+
+
при
(
)
,;0xRR 1
θ
∈− < < .
По признаку Даламбера ряд
()
1
0
1!
n
n
M
R
n
+
∞
=
+
∑
сходится, значит для него
выполняется необходимый признак сходимости и его общий член
()
1
0
1
n
n
MR
n!
+
→∞
→
+
. Значит
(
)
(
)
0
n
n
R
x,xR,
→∞
→∈−R,что и требовалось дока-
зать.
Для разложения функции
(
)
yfx
=
в ряд Тейлора (Маклорена) сле-
дует:
1) составить ряд по формуле;
2) найти его область сходимости;
3) доказать, что для всех x из области сходимости
()
()
()
()
lim 0
n
n
n
Rx f x M
→∞
=≤
.
13.5. Разложение элементарных функций в ряды Маклорена
1.
(
)
x
f
xe= ,
()
()
(
)
(
)
()
()
()
()
01
n
nnn
x
xxR
f
xe e;f fxee== = =≤
на любом интервале
(
)
RRx ,
−
∈
оси
x
, значит для всех
(
)
,x ∈−∞∞.
2
0
1
2
n
x
n
xx
ex ,xR
!n!
∞
=
=+ + + = ∈
∑
…
.
(1)
2.
()
35 21
sh
23521
xx n
ee x x x
x
x ...., x R;
!! n!
−−
−
==++++ +
−
…
∈
(2)
3.
()
22
ch 1
222
xx n
ee x x
x
..., x R.
!n!
−
−
==++++… ∈
(3)

Функциональные ряды
109
4.
(
)
sin
f
xx= ,
(
)
00f ,
=
()
cos sin
2
f
xxx,
π
⎛⎞
′
== +
⎜⎟
⎝⎠
(
)
01f ,
′
=
()
sin sin 2
2
f
xxx,
π
⎛⎞
′′
=− = +
⎜⎟
⎝⎠
(
)
00f
′
′
=
,
()
()
sin
2
n
f
xxn,
π
⎛⎞
=+
⎜⎟
⎝⎠
()
()
0sin
2
n
n
f
.
π
=
()
()
35 21
0
sin 1 1
35 21
n
n
n
xx x
x
x,
!! n!
+
∞
=
=− + − = − ≤
+
∑
… x.
(4)
5.
(
)
cos
f
xx= .
Разложение функции
cos
x
получим дифференцированием ря-
да для
()
sin 4
x
:
()
()
246 2
0
cos 1 1 1
246 2
n
n
n
xxx x
x
,x
!!! n!
∞
=
=− + − + = − ≤
∑
… .
(5)
6.
(
)
(
)
ln 1 1fx x, x=+ >−.
Продифференцируем
()
f
x и разложим производную по фор-
муле суммы бесконечно убывающей геометрической прогрес-
сии:
()
23
1
ln 1 1 , 1 1.
1
xxxx
x
x
′
+= =−+−+ −<<⎡⎤
⎣⎦
+
…
Проинтегрируем это равенство почленно:
() () ()
∫
∑∑
∞
=
+
∞
=
+
+
−=
⎟
⎠
⎞
⎜
⎝
⎛
−=+
0
1
0
,
1
111ln
n
n
n
n
n
n
C
n
x
dxxx
постоянную С найдем, полагая
0x
=
.
1
ln1 0 0.
n
CC
∞
=
=
+⇒=
∑
()
(
)
234
1
0
1
ln 1
234 1
n
n
n
xxx
x
x
n
∞
x
+
=
−
+=−+− +=
+
∑
…
()
1
1
1
,1
n
n
n
xx
n
+
∞
=
−
=−
∑
1.<≤
Здесь учтено, что разложение остается справедливым и
при
1,
x
=
так как ряд сходится по признаку Лейбница.
(6)
7.
(
)
arc tg
f
xx=

Лекции 12 - 14
110
Представим
2
0
arc tg .
1
x
dt
=x
t
+
∫
По формуле суммы бесконечно убывающей геометрической
прогрессии
246
2
1
11
1
ttt , x
t
=− + − + −< <1.
+
…
()
35
24
0
arctg 1 .
35
x
xx
xttdtx=−+− =−+−
∫
……
()
35 21
1
arctg
n
n
xx x
xx
−
−
=− + −…
1
35 21
n
n
=
−
Здесь но, что при
1
1 , 1 1.
x
∞
= − −≤≤
∑
учте
x
=
±
ченный ряд сходится полу по
признаку Лейбница.
При
1
x
= получаем ряд Лейбница для вычисления числа
π
:
11
1.
435
π
=
−+−…
(7)
(
)
(
)
1,
m
f
xx=+ m - произвольное постоянное число.
() ( )
1,
m
f
xx=+
(
)
01f
=
() ( )
1,fx m x
′
=+
1m−
(
)
0
f
m
′
=
(
)
(
)
(
)
2
11 ,
m
fx mm x
−
′′
=−+
(
)
(
)
01fmm
′
′
=
−
……………………………………………………………………
(
)
(
)
(
)
(
)
(
)
111
mn
n
fxmm mn x
−
=− −−+⎡⎤
⎣⎦
…
(
,
)
(
)
(
)
01 1.
n
fmm mn=− −−
⎡⎤
⎣⎦
…
()
()
(
)
(
)
11
1
2
11
12 123
mm m n
mm
m
n
xmx x x
n
−−−
⎡⎤
−
⎣⎦
+=++ ++ +
=
⋅⋅⋅
…
……
…
(
)
(
)
()
,1.
!
n
n
xx
n
+ ∈−
∑
…
1
11
11
mm m n
∞
=
−−+
=
(8)
8.
Область сходимости этого ряда находится по признаку Далам-
бера:
()
(
)
()( ) ()
1
1
1
lim lim
11 1
n
n
n
nn
n
mm m nx n!
u
R
+
un!mmmnx
+
+
→∞ →∞
−−
== =
−−−
⎡⎤
⎣⎦
…
…
=
lim 1
1
n
nm−
xx
n
→∞
=
<
+
.
но доказать, чтоМож
(
)
0
n
n
Rx
→∞
→ для
(
)
1,1x
∈
− .
