Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов

Подождите немного. Документ загружается.

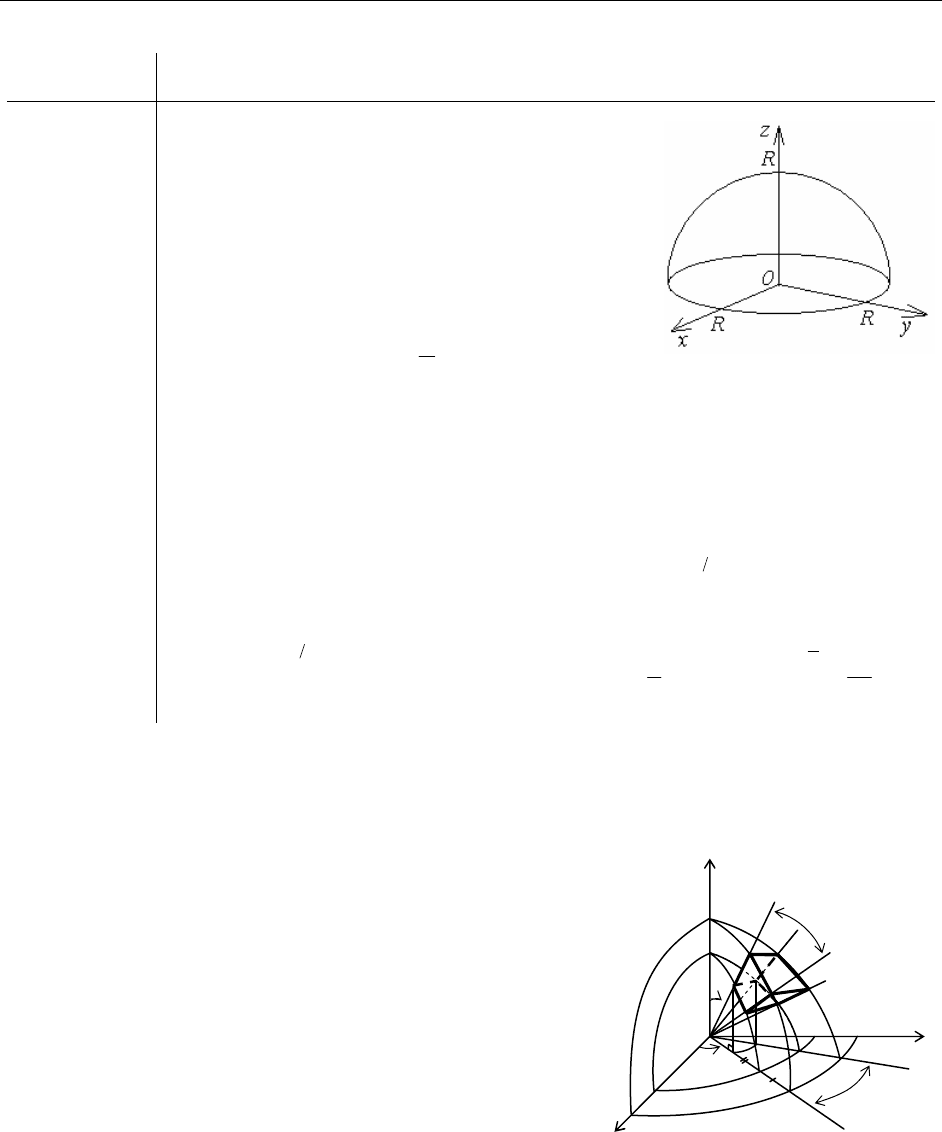
Кратные интегралы

Пример:

Вычислите

, где - верхняя

половина шара

∫∫∫

dxdydzyx )(

2222

Rzyx ≤++

Решение:

Введем сферические координаты. Новые пе-

ременные изменяются в пределах:

0,20,0

θπϕρ

≤≤≤≤≤≤ R .

Тогда

2 2 22 2 22 2 22

sin cos sin sin sin .xy

θϕρ θϕρ

+= + =

В результате

()

22 43 4 3

00 0

42 43

00 0

212

x y dxdydz sin d d d d sin d d

d (cos )d(cos ) d cos cos R .

ρθρθϕρρ θθϕ

πρ ρ θ θ πρ ρ θ θ π

′

+= = =

⎡⎤

=−=−

⎢⎥

⎣⎦

∫∫∫ ∫∫∫ ∫ ∫ ∫

∫∫ ∫

3.4.1. Элемент объема в сферических координатах

∆

′

∆

Вычислим элемент объема в сфериче-

ских координатах. Разобьем область на эле-

ментарные части

координатными по-

верхностями:

V∆

= – сферы,

– кони-

ческие поверхности с вершиной в начале

координат,

– полуплоскости, прохо-

дящие через ось

Oz .

Здесь

=∆ ; из :OCC

′

∆

′

cos(90 ) sin

θρ

=−=

. Дуги

∆ ,

sinAD CK C K C O

ρθ

′′ ′

== =⋅∆= ⋅∆

С точностью до беконечно малых высшего порядка элементарный объем

∆

можно считать параллелепипедом с ребрами

∆

и sin

θϕ

∆ .

Элемент объема

sinV

ρθθ

∆≈ ∆ ∆∆

sindV d d d

ρθθ

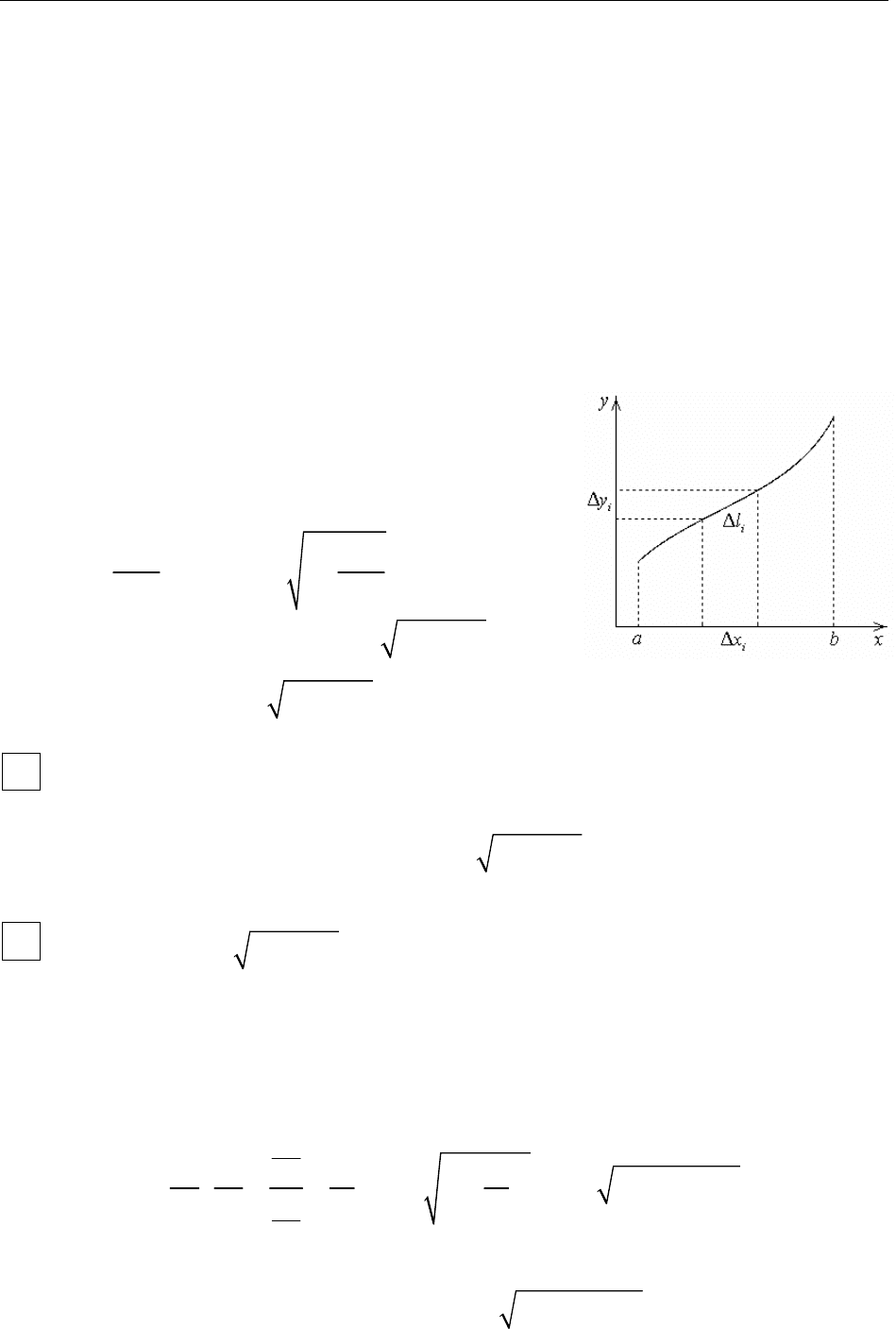
Лекция 1 - 4

4.1. Криволинейные интегралы первого типа (рода)

Рассмотрим фигуру, которая является плоской либо пространственной

кривой

Ф→L. Интеграл по фигуре в данном случае является криволинейным

интегралом первого рода от функции ()

P по кривой L:

() lim ()

Pdl f P l

→

∆

∑

∫

∈

4.1.1. Криволинейный интеграл первого типа по плоской кривой

Пусть плоская кривая задана уравнением

:().

Выберем бесконечно малый участок

∆

на

отрезке

ax . Тогда , b≤≤

lx∆≈∆+∆

(1 )

∆

∆≈+ ∆

∆

∆≈ + ∆

∆

. Переходя к

пределу при

, имеем 0

x∆→

1( )

dl y dx

′

=+ ,

(, ) (, ())1 ( )

x y dl f x x y dx

′

∫∫

Чтобы вычислить криволинейный интеграл первого типа по плоской

кривой, необходимо переменную

заменить на выражение ()y yx

= (из

уравнения линии), а

заменить на dl

1( )

ydx

′

+ и вычислить определен-

ный интеграл по

Величина

1( )

dl y dx

′

=+ называется дифференциальным элементом

длины плоской кривой.

Если линия задана в параметрическом виде:

()

yyt

⎧

⎨

⎩

≤≤ , то

dy dt y

dt dx x

′

=⋅= =

′

1( ) () ()

ttt

dl x dt x y dt

′

′′′

=+ = +

′

;

(, ) ((), ()) ( ) ( )

xydl f xt yt x y dt

′′

∫∫

Кратные интегралы

4.1.2. Криволинейный интеграл первого типа

по пространственной кривой

()

:()

()

zzt

⎧

⎪

⎨

⎪

⎩

≤≤ ,

222

() () () ;

ttt

dl x y z dt

′′′

=++

222

(,,) ((),(),()) ( ) ( ) ( )

ttt

xyzdl f xt yt zt x y z dt

′′′

∫∫

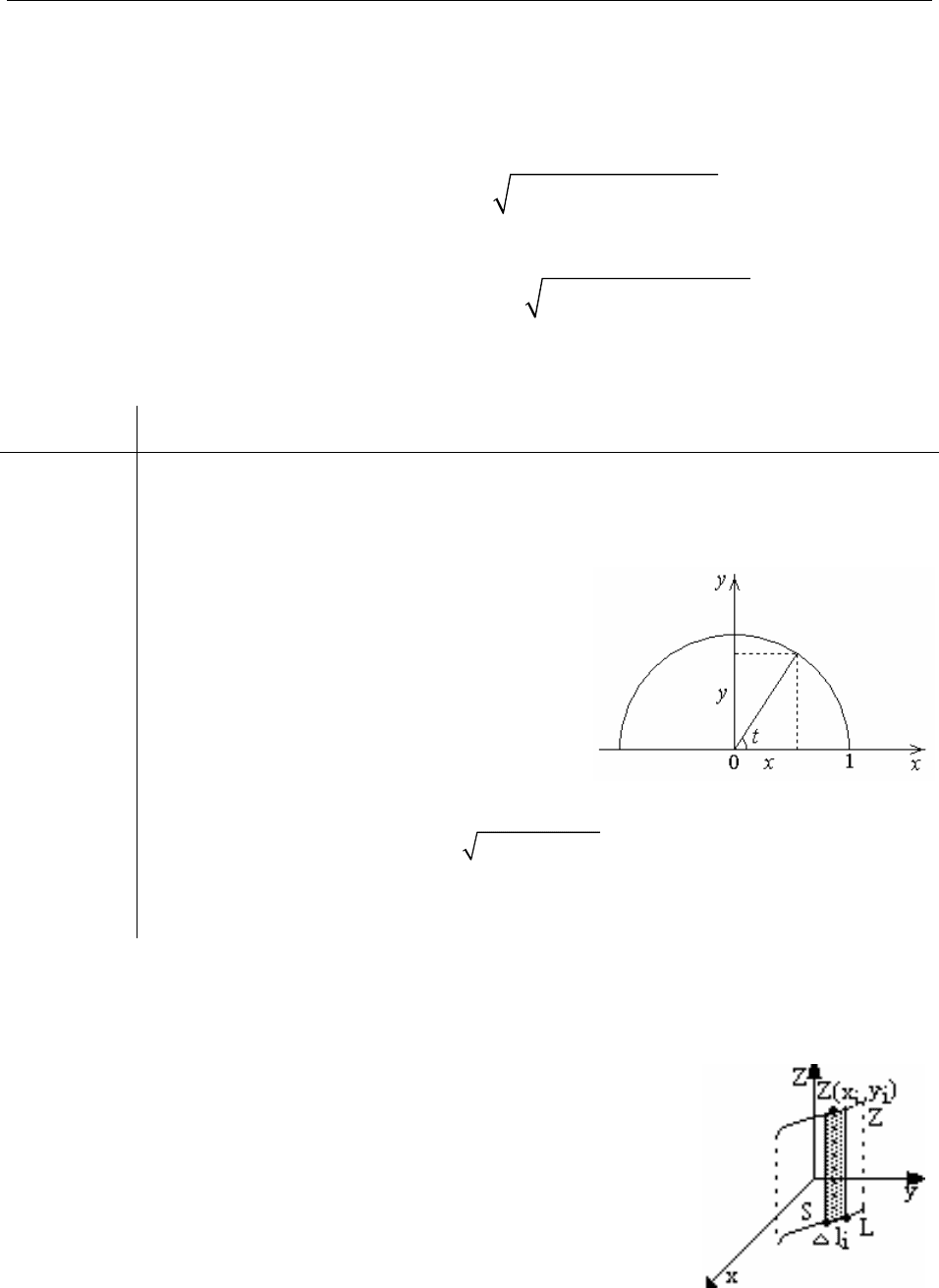
Пример:

Найти массу полуокружности, заданную уравнениями:

⎧

⎨

≥

⎩

Линейная плотность

(, ) .

yky

Уравнение полуокружности в параметри-

ческом виде имеет вид

cos t,

:y sint,

ot .

⎧

⎪

⎨

⎪

≤

⎩

( , ) sin sin cos sin

LLo o

m xydl kydlk t t tdtk tdt

ππ

=== +=

∫∫∫ ∫

(cos) (11) 2

ktk k

=− = +=

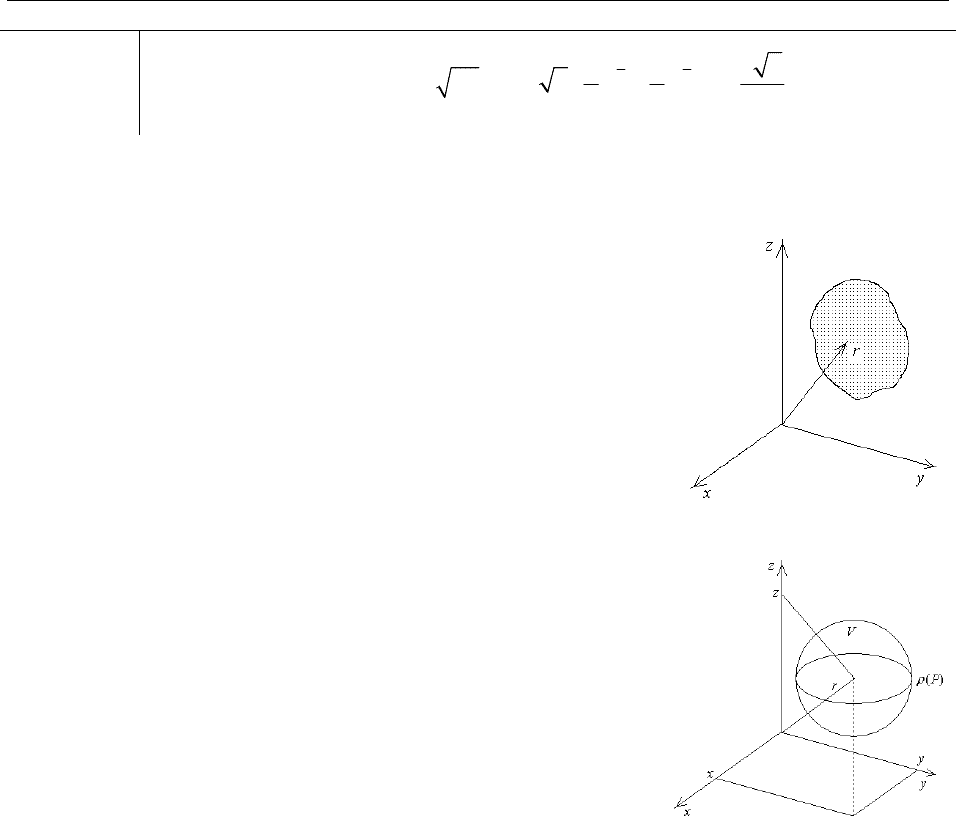
4.1.3. Геометрический смысл криволинейного интеграла

первого типа по плоской кривой

Пусть на плоскости

Oy задана кривая L. На

множестве

L определена функция () (,zfP fx)y

= .

Разобьем кривую

L на n частей

длиной

∆

. Выбе-

рем на кривой

L точку , вычислим значение функ-

ции

Тогда площадь прямоуголь-

ного участка равна

() (, ).

zfP fxy==

(, )

iii

Sfxy

∆

=∆.

Найдем сумму площадей

(, )

ii i

xy l

∆

∑

Перейдем к пределу при

, тогда n →∞

Лекция 1 - 4

1=y

yx 2

2=+ zy2

pdl

lim ( , ) ( )

ii i

Sfxylf

→∞

=∆=

∑

∫

Таким образом, криволинейный интеграл первого

типа по плоской кривой

численно равен площади боковой поверхности цилиндра с направляющей

L и

образующей, длина которой () (,)

zfP fxy

= .

4.2. Механические приложения интегралов по фигуре

4.2.1. Длина, площадь, объем фигуры

Длина отрезка равна

, площадь плоской фигуры равна ,

ld=

∫

x y

xdydz=

∫∫∫

Sdxd=

∫∫

объем тела Vd.

4.2.2. Масса фигуры

Масса неоднородного тела с плотностью (, ,)

(, ,)

m x y z dxdydz

∫

∫∫

Пример:

Найдите массу тела, ограниченного цилиндрической поверхностью

и плоскостями

, если в каждой его точке плотность

1, 2 2yz yz+= +=

(, ,)

yz y

= .

Решение:

Из

получаем, что при

1yz+=

, а при ; из

получаем, что при

1z = yz+=

, а при 0y

. 2z =

Линии пересечения плоскостей с

координатной плоскостью : zOy

1zy

− и

. 2(1 )zy=−

В плоскости

Oy направляющей цилинд-

рической поверхности является парабола

y= .

Проекция тела на плоскость

D огра-

ничена линиями:

, 0

y = 1y

≤

≤ ;

y=± , 22yx y−≤≤ .

()

2(1 )

(1 )

VDyD

m ydxdydz ydxdy dz y y dxdy y y dy dx

−

== =−=−

∫∫∫ ∫∫ ∫ ∫∫ ∫ ∫

Кратные интегралы

()

22 8

22 22

57 3

yy ydy y y

⎛⎞

=− = − =

⎜⎟

⎝⎠

∫

4.2.3. Момент инерции фигуры

Рассмотрим систему из n материальных точек с

массами

, . Момент инерции системы от-

носительно некоторой оси вращения

J = , где

— расстояние от

i –й точки до оси вращения. Если

тело сплошное, то возникает интеграл по фигуре

12i , ,...,n=

∑

()rPd

∫

Осевые моменты (моменты инерции фигуры

относительно осей координат). Рассмотрим про-

странственную фигуру

Ф→V.

J - момент инерции относительно оси Оx (мера

инертности тела при вращении относительно оси

Оx):

()(,,)

Jyzxyz

∫∫∫

()(,,)

Jxzxyz

∫∫∫

()(,,)

Jxyxyz

∫∫∫

Моменты инерции относительно координатных плоскостей:

(, ,)

Jzxyz

∫

∫∫

(, ,)

Jyxyz

= dV

∫

∫∫

(, ,)

Jxxyz

= dV

∫

∫∫

Полярный момент (момент инерции относительно начала координат, где

центр

О – полюс):

222

()(,,

Jxyzxyz

=++

∫∫∫

)dV

Лекция 1 - 4

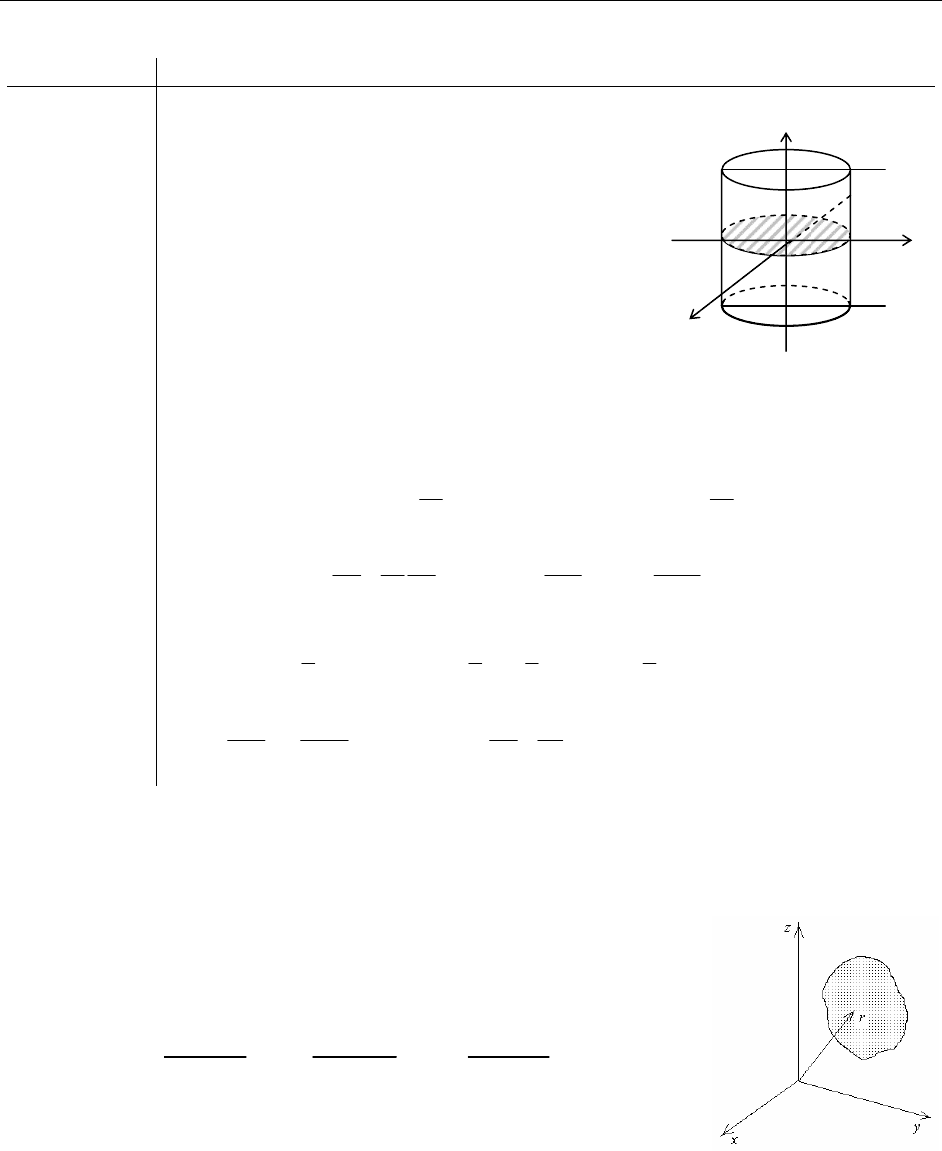
Пример:

Найдите момент инерции однородной

боковой поверхности цилиндра, зада-

ваемой уравнениями:

22 2

xzR

ππ

⎧

⎪

⎨

−≤≤ ≥

⎪

⎩

1)(

≡

Решение:

2222

xy x y

Jzdz(z)(z)dS

∑

′′

== ++

∫∫ ∫∫

∫∫∫∫

−

⋅−=

−

+−=

RxRdS

)(1)(

=−=−=−=

∫∫∫∫∫

−

dxxRRdydxxRRdxdyxRR

2222

xRsint

dx R costdt

sint

t arcsin

ππ

⎧

⎫

⎪

⎨

⎬

⎪

−≤≤

⎪

⎩⎭

222

sin cos cos cos

RR tRtdt RRtRtdt

ππ

−−

=− = =

∫∫

32 2

cosdt t

os2

cos

−

⎧⎫

⎨⎬

⎩⎭

∫

Кратные интегралы

Пример:

Вычислите момент инерции прямого кругового цилиндра высотой и

радиусом R относительно диаметра его сред-

него сечения, считая плотность постоянной и

равной

()

∫∫∫

+==

dxdydzzyII

Решение:

Перейдем к цилиндрическим координатам:

cos , sin , ;

yzz

ϕρϕ

===

dzdddxdydz

22222

sin zzy +=+

ϕρ

() ()

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

+⋅=

⎥

⎦

⎤

⎢

⎣

⎡

=+=+=

∫∫

∫∫∫∫

∫∫∫∫∫∫

ϕϕγ

ρρ

ϕϕγ

ρϕρρϕγϕρρρϕγ

ϕρρρϕγϕρργϕρ

ππ

RhhRh

zdd

dzzddzdddzI

sin

234

sin2

sin2sin

234

222

()

2sin

2cos1

sin

234

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎪

⎭

⎪

⎬

⎫

⎥

⎦

⎤

⎢

⎣

⎡

−=−

⎪

⎩

⎪

⎨

⎧

∫∫

RhhR

πγππγ

ππϕϕϕϕϕϕ

ππ

−

4.2.4. Статические моменты фигуры. Центр тяжести фигуры

Рассмотрим n материальных точек массой m

Координаты центра тяжести системы точек:

11 1

;;

nn n

i ii ii

ii i

CC C

nn n

ii i

mym zm

XYZ

mm m

== =

∑∑ ∑

∑∑∑

где величины, равные

yz i i

⎫

⎪

⎬

⎪

⎭

∑

, называют ста-

тическими моментами системы относительно плоскостей yОz, xОz, xОy.

Лекция 1 - 4

1). Если система (фигура) имеет центр симметрии, ось симметрии, плос-

кость симметрии, то статические моменты соответственно относительно

центра, оси, плоскости равны нулю.

2). Если фигура непрерывна, то вместо сумм возникают соответствую-

щие интегралы по фигуре

() () ()

;;

() () ()

CCC

Pd y Pd z Pd

xyz

Pd Pd Pd

ΦΦΦ

µρµρµ

µρµρ

===

∫∫∫

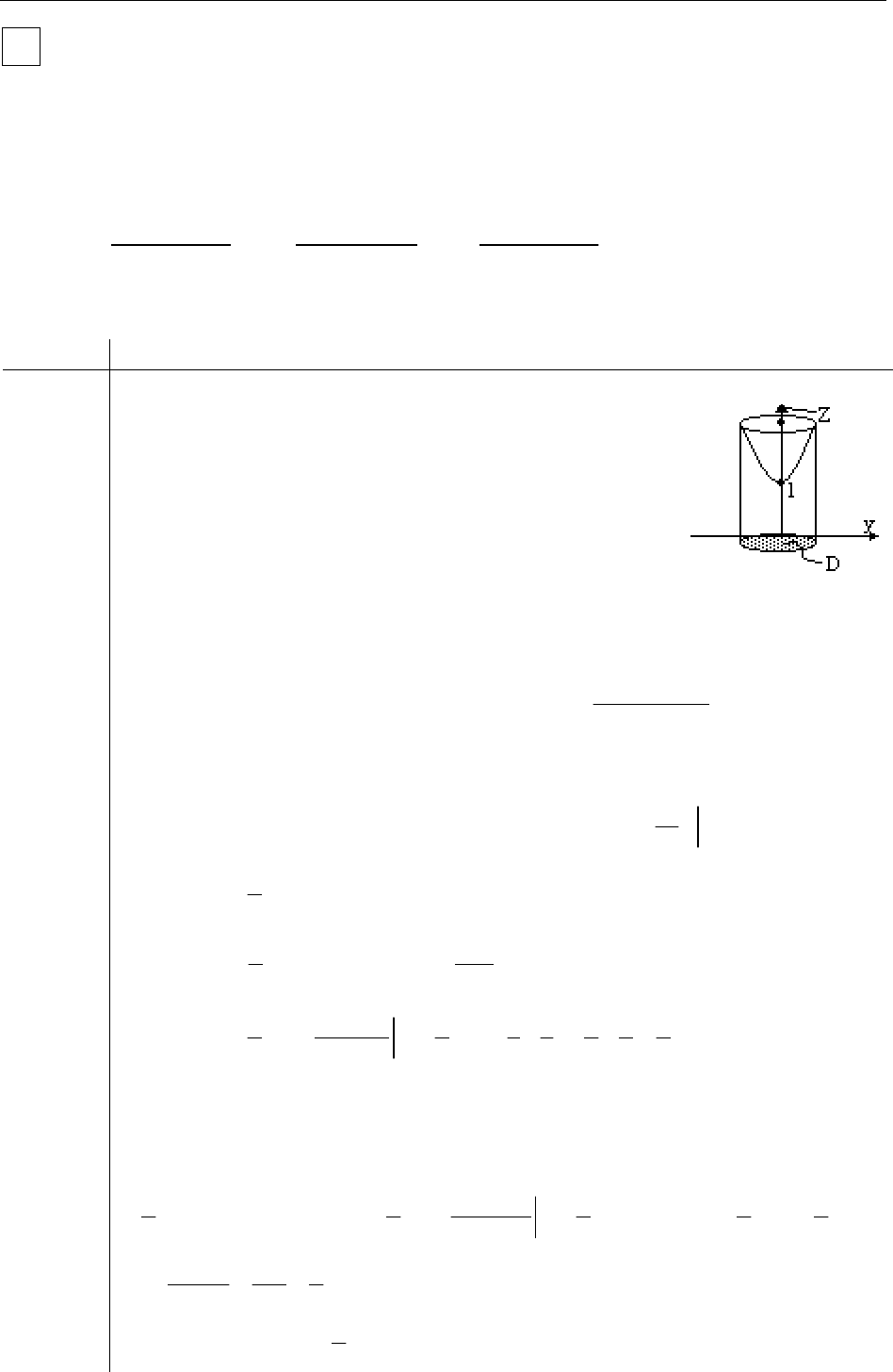
Пример:

Найдите центр тяжести однородного (() 1P

) цилин-

дра, ограниченного поверхностями:

zx y ,

⎧

⎪

⎨

⎪

⎩

Сверху цилиндр ограничен эллиптическим параболои-

дом.

Решение:

Из соображений симметрии х

= 0, у

= 0, т.к. статические моменты относи-

тельно плоскостей ZOY и ZOX равны нулю,

()

zPdV

PdV

∫∫∫

Числитель:

()

VVD D

z P dV zdV dS zdz ds

∫∫∫ ∫∫∫ ∫∫ ∫ ∫∫

22 2

(1)

ds x y=++=

∫∫

{в полярных координатах}

∫∫∫∫

=+=

)1(

rdrrd =++

⋅

222

)1()1(

rdrd

1(1)1 81277

()

4343343

ππ

ϕπ

==−=

∫∫

Знаменатель:

000

(1)

dV ds dz d r rdr

==+

∫∫∫ ∫∫ ∫ ∫ ∫

∫∫∫∫

=−=

=++=

πππ

ϕϕϕ

)14(

)1(

)1()1(

drdrd

ππ

=⋅= .

727

63 33 9

⋅⋅

⋅⋅ ⋅

Ответ:

=0, y

=0, z

Кратные интегралы

Пример:

Определите координаты центра тяжести верхней половины шара радиусом R

с центром в

, считая плотность )0,0,0(

постоянной.

Решение:

222 22

;0;0zRxyz zRxy=−− =≤≤−−

xy==

zdxdydz

dxdydz

∫∫∫

В сферических координатах:

ϕθθρρθρ

ddddxdydzz sin,cos

()

000

sin sin

2 sin 2 sin cos

33 3

mdddddd

ππ

γρρθθϕ ϕ θγρρθ

πγ

πγ θ θ πγ θ θ θ

πγ

== =

===−

∫∫∫ ∫ ∫ ∫

∫∫

00 0

cos in cos sin

sin

2 sin (sin ) .

4224

sddd d d d

ρθρ θρθϕγ ϕ θθθρρ

πγ πγ

γπ θ θ

===

∫∫∫ ∫ ∫ ∫

∫

42 8

πγ

==.

Ответ:

=0, y

=0, z

В результате изучения материала, изложенного в этих лекциях,

студент должен знать следующие понятия и уметь вычислять:

 интегралы по фигуре, их классификацию и свойства;

 двойной интеграл, вычисление двойного интеграла как повторного;

замена переменных в двойном интеграле, двойной интеграл в полярных

координатах;

 поверхностный интеграл первого рода, способы вычисления;

 тройной интеграл, вычисление тройного интеграла как повторного;

способы его вычисления, замена переменных в тройном интеграле;

тройной интеграл в цилиндрических координатах;

тройной интеграл в сферических координатах;

 криволинейный интеграл первого рода, способы вычисления;

 геометрические и механические приложения интегралов по фигуре:

длина, площадь, объем, масса фигуры;

центр тяжести, статические моменты, моменты инерции фигуры.

Лекции 5 – 9

ТЕОРИЯ ПОЛЯ (ВЕКТОРНЫЙ АНАЛИЗ)

Теория поля (или векторный анализ) изучает скалярные и векторные поля, т.е. ска-

лярные и векторные функции точки в пространстве. Хотя объекты теории не связаны с ка-

кой-либо системой координат, использование этого инструмента позволяет, исследуя

средствами математического анализа функции нескольких переменных (которыми стано-

вятся функции точки), определить координатно независимые операции над полями и изу-

чить их свойства. В этом векторный анализ, как раздел

векторного исчисления, полностью

аналогичен векторной алгебре – хотя операция над векторами может быть сведена к вы-

числениям, проводимым над координатами векторов, результат от координатной системы

не зависит.

Понятие поля позволяет наиболее естественно характеризовать и описывать те свой-

ства реальных объектов, которые не зависят от выбора системы координат: реальные фи-

зические свойства не

должны быть связаны с какой-либо системой координат.

5.1. Скалярное поле

5.2. Поверхности и линии уровня

5.3. Производная по направлению

5.4. Градиент скалярного поля

5.4.1. Оператор Гамильтона (набла)

5.4.2. Связь производной по направлению с градиентом

5.4.3. Свойства градиента

5.5. Векторное поле

5.5.1. Векторные линии

5.5.2. Плоское векторное поле

6.1. Односторонние и двусторонние

поверхности

6.2. Площадь поверхности

6.3. Система координат и ориентация поверхности

6.4. Поверхностный интеграл 1-го рода

6.5. Поверхностный интеграл 2-го рода

7.1. Поток векторного поля

7.2. Свойства потока

7.3. Вычисление потока

7.3.1. Проектирование на одну координатную плоскость

7.3.2. Проектирование на три координатные плоскости

7.4. Физический смысл потока

7.5. Дивергенция векторного поля

7.5.1. Свойства

дивергенции

7.6. Физический смысл потока через замкнутую поверхность

7.7. Теорема Остроградского – Гаусса

7.8. Инвариантное определение дивергенции

7.8.1. Физический смысл дивергенции

8.1. Линейный интеграл в векторном поле

8.2. Свойства линейного интеграла

8.3. Вычисление линейного интеграла