Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов

Кратные интегралы

21

2.4.1. Дифференциальный элемент площади

в полярной системе координат

Разобьем область интегрирования на элементар-

ные ячейки

с помощью координатных линий:

ij

S∆

j

ρ

= - окружности,

i

ϕ

= - лучи, тогда

1jj j

ρ

ρρ

+

∆= −

i

,

1ii

ϕ

+

−

ϕ

∆=

ij

S

. Так как окружности

ортогональны радиусам, то внутренние ячейки

∆

с

точностью до бесконечно малых более высокого

порядка малости относительно их площади можно

рассматривать как прямоугольники со сторонами

ji

ρ

ϕ

⋅∆ и

j

ρ

∆ , поэтому ()

ij j i j

S

ρ

ϕρ

∆≈ ∆ ⋅∆. Ячейками

неправильной формы пренебрегаем. Переходя к пре-

делу, получим, что двумерный элемент площади в

полярных координатах равен

dS d d

ρ

ρϕ

=

.

1). Интегрирование в полярной системе коорди-

нат удобно использовать, когда область

огра-

ничена дугами окружностей.

D

2). В полярных координатах внешний интеграл

при сведении его к повторному может вычис-

ляться по углам.

0

y

ρ

,

x

D

j

ρ

1+j

ρ

1+i

ϕ

i

ϕ

0

y

ρ

,

x

ij

M

ij

S∆

!

0

ρ

D

ϕ

β

ϕ

=

)(

1

ϕ

ρ

)(

2

ϕ

ρ

α

ϕ

=

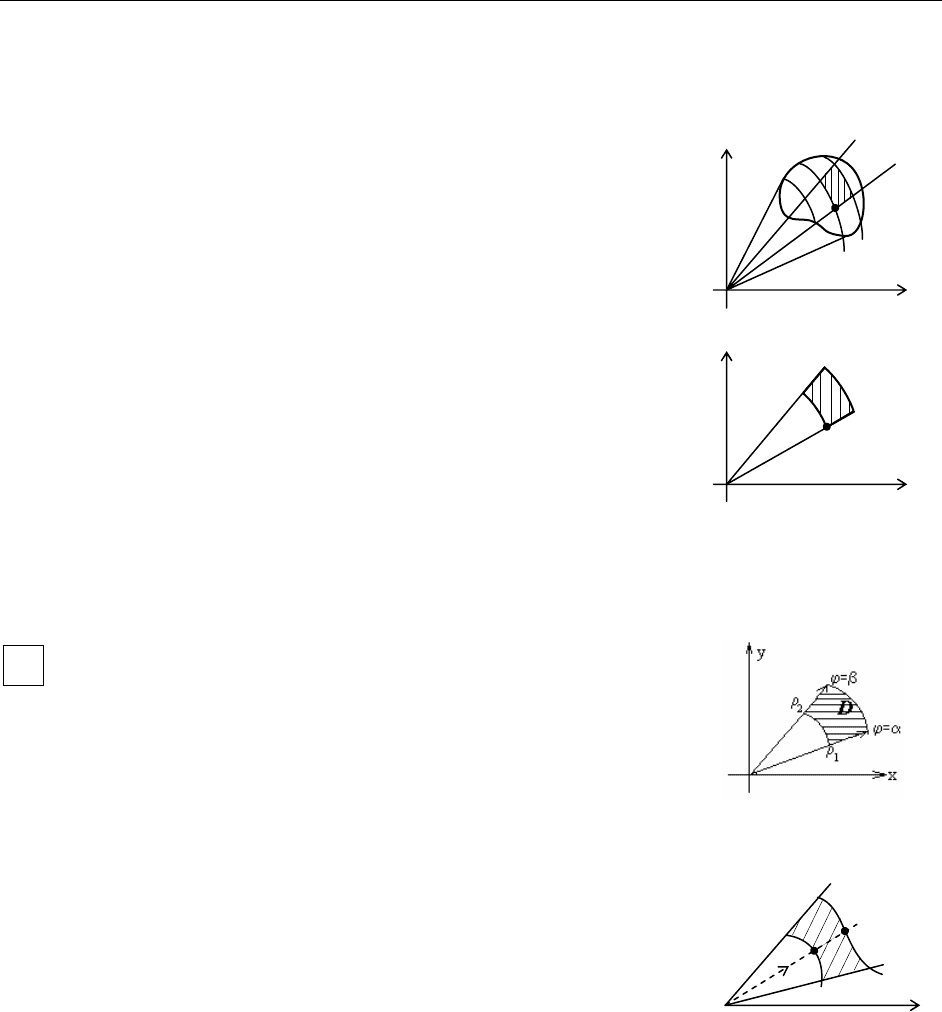
Пусть область интегрирования

D

определяется

неравенствами:

α

ϕβ

≤≤,

12

() ()

ρ

ϕρρϕ

≤

, где

1

()

ρ

ϕ

и

2

()

ρ

ϕ

- однозначные непрерывные

функции на отрезке [, ]

α

β

.

2

1

()

(,) (,)

D

f

dd d f d

ρϕ

β

αρϕ

ρ

ϕρ ρϕ ϕ ρϕρ ρ

=

∫∫ ∫ ∫

.

3). В полярных координатах внешний интеграл может вычисляться и по

полярному радиусу. Пусть область интегрирования

определяется не-

равенствами:

D

12

R

ρ

≤≤ ,

12

() ()

ϕ

ρϕϕρ

≤

≤ , где

1

()

ϕ

ρ

и

2

()

ϕ

ρ

- одно-

значные непрерывные функции на отрезке

[,

12

]

R

R .

22

11

()

(,) (,)

R

DR

f

dd d f d

ϕρ

ρ

ϕρ ρϕ ρ ρ ρϕ ϕ

=

∫∫ ∫ ∫

.

Лекция 1 - 4

22

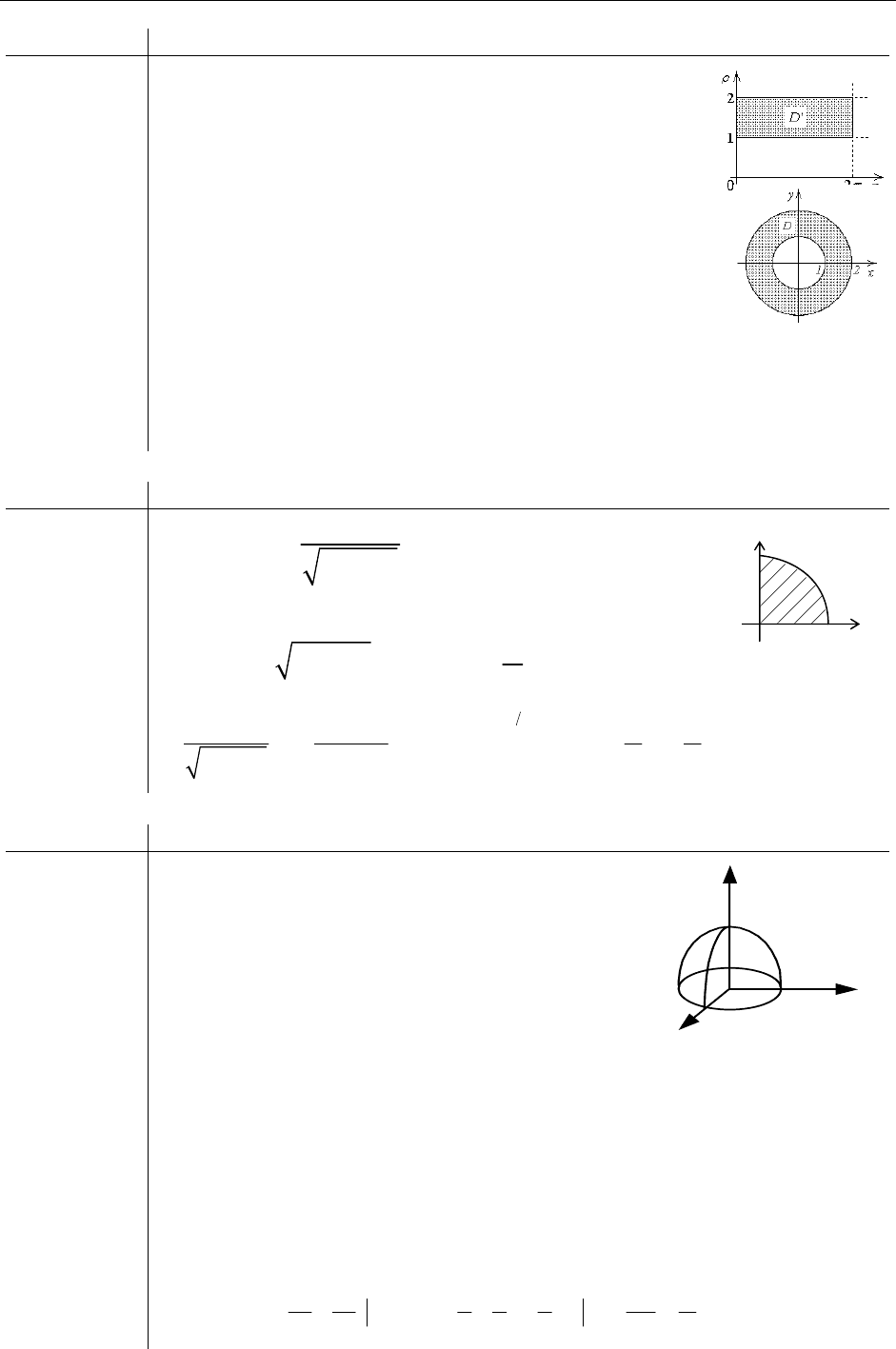
Пример:

Записать в полярных координатах двойной интеграл

по области D:

⎪

⎩

⎪

⎨

⎧

=+

4

1

22

yx

- кольцо.

Решение: полярные координаты

cos , sinxy

ρ

ϕρ

==

ϕ

=

.

22 22 2

1

cos sin 1, 1, 1

ρϕρϕρ ρ

+==,

аналогично

2

ρ

= .

Область интегрирования в полярных координатах —

прямоугольник: 1

D

′

2, 0 2

ρ

ϕπ

≤≤ ≤≤ .

(, ) ( , )

DD

fxydxdy f d d

ρϕρ ρ ϕ

′

==

∫∫ ∫∫

2

01

(,)df d

ρ

π

ρ

ϕ

ρϕρ ρ

=

′

=

∫∫

.

Пример:

Вычислите

22

D

dxdy

x

y+

∫∫

, где - первая четверть круга D

1

R

= с центром в точке

(

)

00O,.

22

x

y=+

ρ

, 0D:

2

π

ϕ

≤

≤ , 01

ρ

≤

≤ .

2

1

22

00

1

22

DDD

dxdy d d

dd d d

xy

π

ρ

ρϕ π π

ρϕ ϕ ρ

ρ

====⋅

+

∫∫ ∫∫ ∫∫ ∫ ∫

=.

Пример:

Найти объем тела, если оно задается поверх-

ностями:

22

1

0

zxy

z.

⎧

=− −

⎨

=

⎩

;

Решение:

Область интегрирования – проекция фигуры

на плоскость

x

Oy . Граница D: -

окружность.

1=

22

+ yx

Перейдем в полярную систему координат:

,

⎩

⎨

⎧

≤≤

=

′

πϕ

20

1

:

r

D

∫∫ ∫∫

=−−==

DD

dxdyyxdxdyyxfV )1(),(

22

21

22

00

(1 ) (1 )

D

r rdrd d r rdr

π

ϕϕ

′

=

−=−

∫∫ ∫ ∫

=

22

24

1

2

0

00

11 1 2

() ()

24 244 4

rr

dd

ππ

π

2

π

ϕϕϕ

=

−= −= ==

∫∫

.

y

0

x

1

D

Кратные интегралы

23

2.5. Поверхностный интеграл первого типа (рода)

Поверхностные интегралы первого типа – это обобщение двойных инте-

гралов по области

D

. Рассмотрим фигуру, которая является поверхностью

; . Интеграл по фигуре в данном случае является поверхностным ин-

тегралом первого рода от функции

Σ

Φ

→Σ

() (,,)

f

Pfxyz

=

по поверхности Σ :

01

(, ,) lim ( )

n

ii

ri

fxyzd fP

σ

→=

∑

=

Σ∆

∫∫

2.5.1. Вычисление поверхностных интегралов первого рода

Вычислим

(

)

,,

f

xyzd

σ

Σ

∫∫



. Пусть

(

)

,, 0fxyz≥ , а поверхность задана

уравнением

Σ

()

,.zfxy=

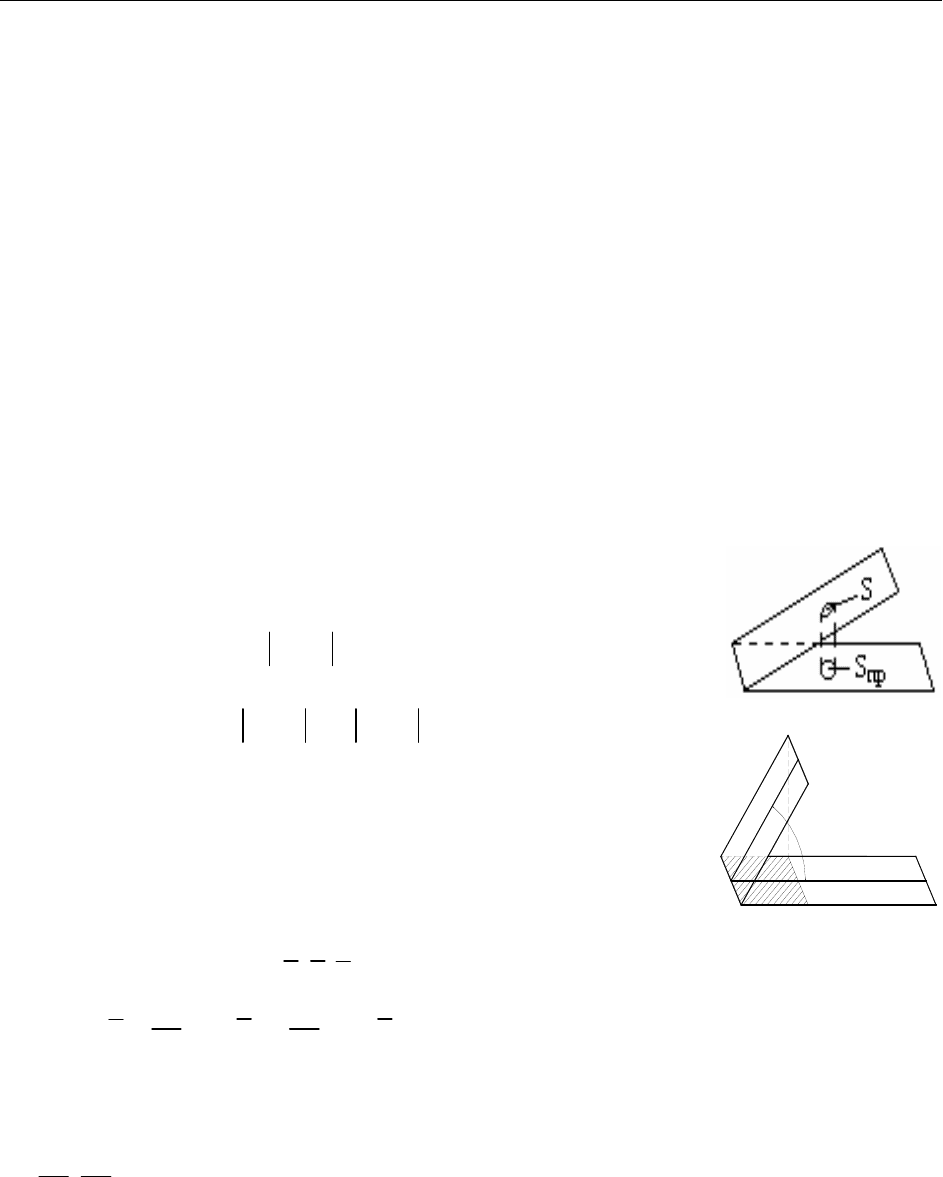
Лемма. Площадь проекции плоского участка одной плос-

кости

на другую равна площади самого участка, ум-

ноженной на модуль косинуса двугранного угла между

плоскостями:

1

P

2

P

cos

пр

SS

ϕ

=⋅ .

Доказательство:

Sla=⋅ ;

cos cos

пр

Sal S

ϕ

=⋅⋅ = (поскольку ,

косинус берется по модулю).

пр

S ≥ 0

Пусть требуется вычислить поверхностный инте-

грал первого рода по поверхности

Σ

. Область

D

являет-

ся проекцией поверхности

на плоскость Σ

x

Oy . Через

точку поверхности

(

,,

)

A

xyz проведем касательную плоскость. Ее уравне-

ние:

()(

zz

zz xx yy

xy

∂∂

−= − + −

∂∂

)

. Выберем часть поверхности

d

σ

и спроек-

тируем ее на касательную плоскость. Обозначим проекцию .d

σ



Будем счи-

тать ~dd

σ



. Обозначим n





- нормаль к касательной плоскости:

,,1

zz

n

xy

⎛⎞

∂∂

−

⎜

∂∂

⎝⎠



⎟

. Поскольку

(

)

0,0,1k





- нормаль к

x

Oy , то угол

ϕ

- угол между

касательной плоскостью и плоскостью Ox равен углу между векторами y n





и



.

k

P2

P1

l

a

ϕ

Найдем связь между (проекцией ddS

σ



на плоскость

x

Oy ) и d

σ



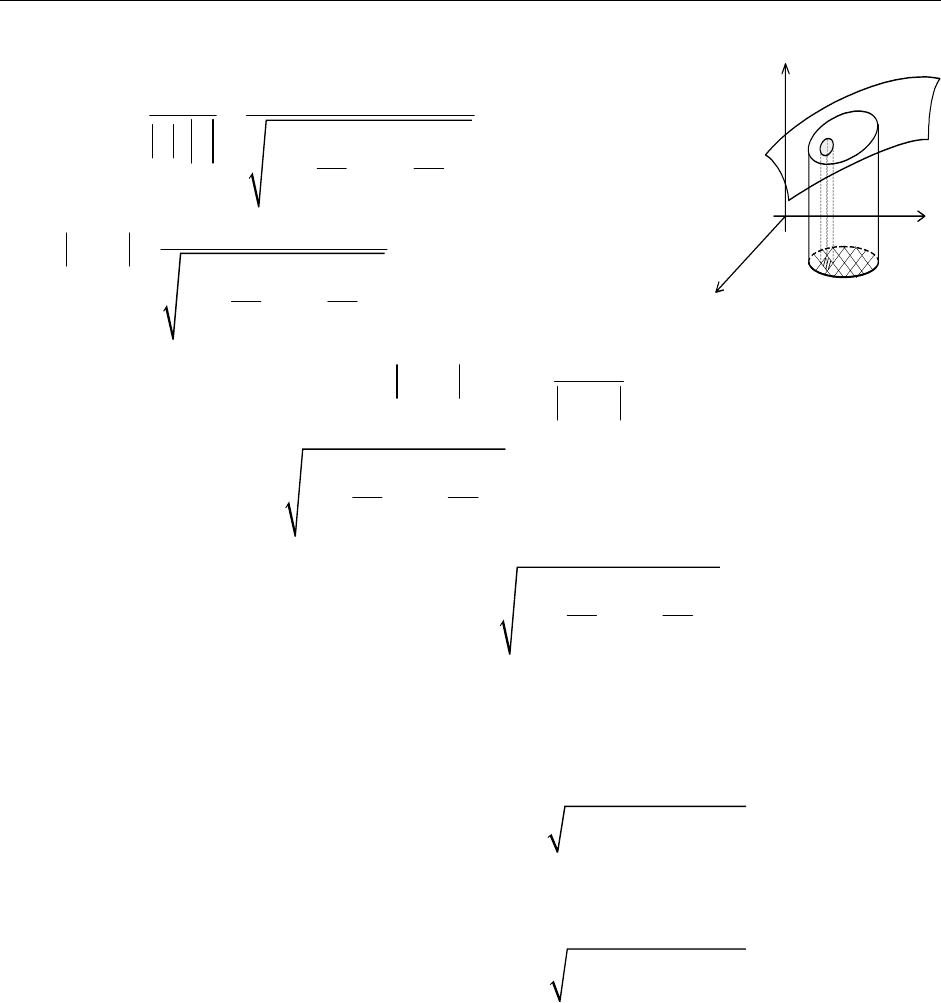
Лекция 1 - 4

24

()

2

,

1

cos

1

nk

zz

x

y

ϕ

−

==

⋅

⎛⎞

∂∂

⎛⎞

++

⎜⎟

∂∂

⎝⎠



;

2

1

cos ;

1

zz

xy

ϕ

=

⎛⎞

∂∂

⎛⎞

++

⎜⎟

∂∂

⎝⎠



в пределе при

0, , cos ,

cos

n

dS

r dddSd d

σσ σ ϕ σ

ϕ

→= =⋅ =



  

;

0

x

y

z

D

Γ

),( yxfz =

2

1

zz

ddS

x

y

σ

⎛⎞

∂∂

⎛⎞

=⋅+ +

⎜⎟

∂∂

⎝⎠

;

() ()

()

2

,, ,, , 1

xy

D

zz

fxyzd fxyzxydS

x

y

σ

Σ

⎛⎞

∂∂

⎛⎞

=⋅+

⎜⎟

∂∂

⎝⎠

∫∫ ∫∫

+

.

Так записывается поверхностный интеграл, если поверхность задана уравне-

нием

(

)

,.zzxy=

Если поверхность задана уравнением

(

)

,,yyxz

=

то

() ()

()

() ()

22

,, , , , 1

xz

D

f

xyzd f xyxz z y y dS

σ

Σ

′′

=⋅+

∫∫ ∫∫

+⋅

.

Аналогично, если

(

)

,,

x

xyz= то

() ()

()

2

,, , ,, 1

yz

D

f

xyzd f x yz yz x x dS

σ

Σ

′′

=⋅++

∫∫ ∫∫

⋅,

где ,

x

zy

DD

z

- проекции на плоскости . Σ ,Oxz Oyz



Кратные интегралы

25

3.1.Тройной интеграл

Рассмотрим фигуру, которая является пространственной областью .

Интеграл по фигуре в данном случае является тройным интегралом от функ-

ции

G

() (,,)

f

Pfxyz= по пространственной области G :

() () ()

0

1

,, ,, lim .

n

ii

r

i

G

f

xyzd f xyzdV f P V

µ

→

=

Φ

==

∑

∫∫∫∫

∆

Область G будем называть правильной в направлении оси , если: Oz

1) любая прямая, параллельная оси , пересекает границу области G не бо-

лее чем в двух точках;

Oz

2) область проектируется на координатную плоскость в правильную

плоскую область

G Oxy

D

;

3) любая часть области G удовлетворяет первым двум пунктам.

Примером таких областей является эллипсоид, куб, параллелепипед.

3.1.1. Задача о вычислении массы тела

Пусть область является правильной в

направлении оси , то есть ограничена снизу

и сверху соответственно однозначными непре-

рывными поверхностями:

V

Oz

11

(,zz )xy

=

и

, причем проекцией области на

координатную плоскость является пло-

ская область

22

(, )zzxy= V

Oxy

D

, ограниченная линиями:

(

)

(

)

12

,,,yyx yyx xaxb===

  

.=

Прямая, параллельная оси , пересекает координатную плоскость

и поверхности

и

Oz Oxy

11

(, )zzxy=

22

(, )zzxy

=

, соответственно, в точках

(, ,0)

M

xy

,

11

(, , )

M

xyz

,

2

(, , )

2

M

xyz

. Отсюда следует, что при фиксированных значени-

ях (, )

x

yD∈ соответствующие аппликаты точек области V изменяются в

пределах:

.

z

12

(, ) (, )zxy z z xy≤≤

Пусть тело материально, а объемная плотность V () (,,)Pxyz

ρ

ρρ

=

= =

=

(

)

,,

f

xyz . По физическому смыслу интеграла по фигуре

. Вычислим массу данного тела. Для этого рассечем тело

()

,,

V

mxyz

ρ

=

∫∫∫

dV

0

x

y

z

a

x

b

y

c

d

2

M

),(

2

yxz

M

D

1

M

V

),(

1

yxz

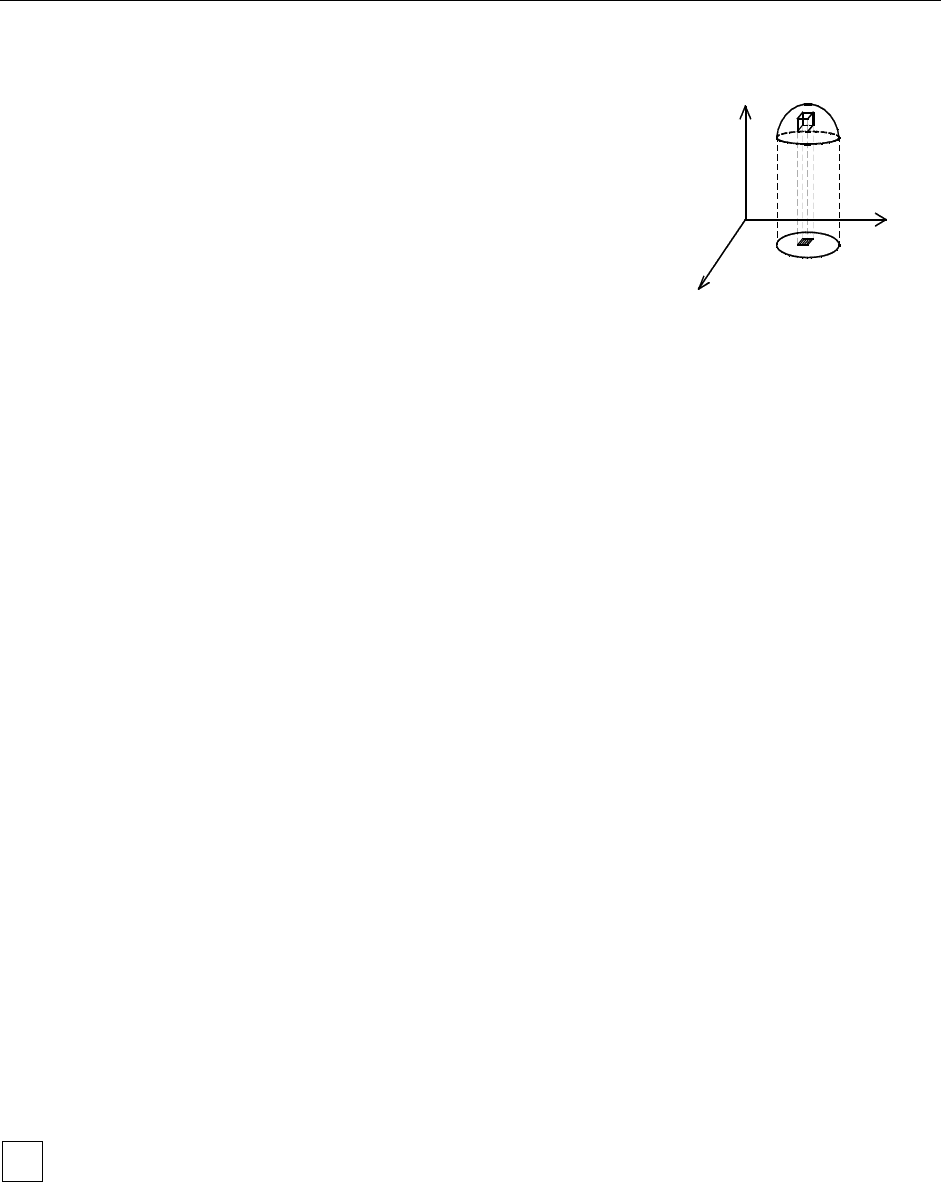
Лекция 1 - 4

26

плоскостями, параллельными координатным плоскостям:

,

x

xx

yy y

zz z

+∆

⎫

⎪

+∆

⎬

⎪

+∆

⎭



i

z

D

Y

X

Z

1(x,y)

Z

2(x,y)

.

Этими плоскостями тело разбивается на паралле-

лепипеды, объем каждого из которых равняется

. Выберем в пределах каждого

из них по точке

iii

Vxy∆=∆⋅∆⋅∆

(, ,)

iiii

M

xyz

.

Примем приближенно, что в пределах части

i

V

∆

плотность постоянна и

равна (, ,)

iii

x

yz

ρ

. Тогда масса части

i

V

∆

равна

(

)

,,

iiii

mxyz

i

V

ρ

≈⋅∆,

(

)

,,

iiiii

mxyzS

i

z

ρ

≈⋅∆⋅∆ V, а масса всего тела равна

1

(, ,)

n

iii i

i

mxyz

ρ

=

≈

∆

∑

. Если

диаметры всех элементарных частей стремятся к нулю, то в пределе это ра-

венство становится точным и

max 0

1

lim ( , , )

n

iii i

d

i

mxyzV

ρ

→

=

∆

∑

0

n

r → V

S

, , ,

. Вычислим массу столбика с основанием dS :

i

Vd∆→

i

Sd∆→

()

(

)

2

1

,

,,

zxy

i

zxy

mdS xyzdz

ρ

=

∫

.

Масса всего тела

,

следовательно,

max 0

1

lim

i

n

i

d

i

mm

→

=

=∆

∑

i

S

()

(

)

2

1

,

,,

zxy

Dzxy

mdS xyzd

ρ

=

∫∫ ∫

z.

Таким образом

() ()

()

(

)

2

1

,

,, ,,

zxy

VDzxy

f

xyzdV dS xyzdz

ρ

=

∫∫∫ ∫∫ ∫

.

!

Для вычисления

необходимо вычислить интеграл по переменной ,

считая

V

∫∫∫

z

x

и фиксированными переменными, а затем вычислить y

∫

по

проекции этого тела

D

на плоскость

x

Oy :

() ()

()

(

)

()

(

)

22

11

,

,, ,,

yx zxy

b

Vayxzxy

f

xyzdV dx dy f xyzdz=

∫∫∫ ∫ ∫ ∫

.

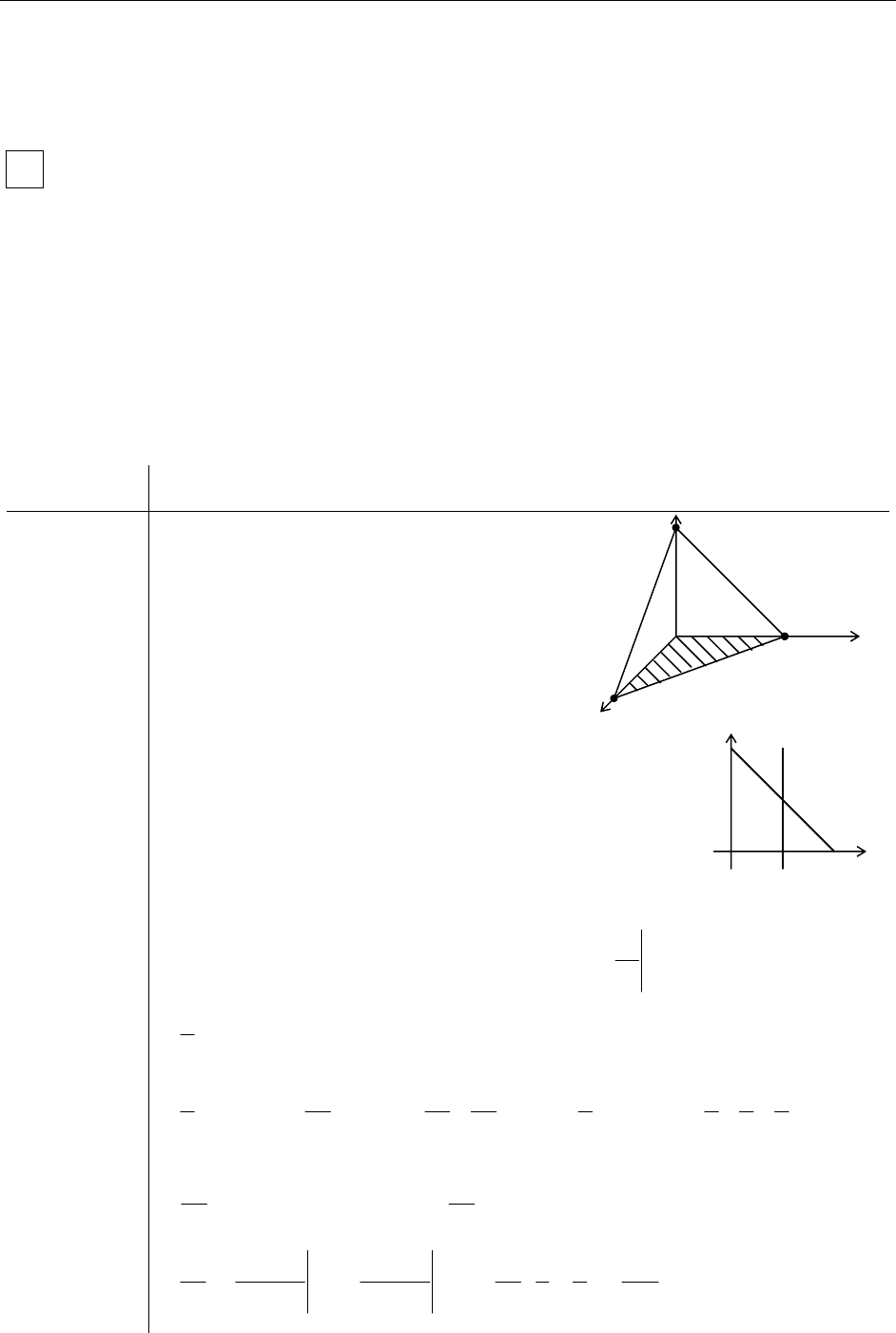
Кратные интегралы

27

Таким образом, чтобы вычислить

∫

∫∫

по правильной области V , необ-

ходимо вычислить трехкратный повторный интеграл.

1). называют дифференциальным элементом объема в де-

картовой системе координат.

dV dxdydz=

2). В повторных интегралах пределы интегрирования могут зави-

сеть только от тех переменных, по которым еще не проведено интегри-

рование. Внешний интеграл всегда вычисляется в постоянных пределах.

3) Если область

D

задана неравенствами cyd

≤

≤ ,

12

() ()

x

yxxy≤≤ , то

() (,)

22

() (,)

11

(, ,) (, ,)

xy zxy

d

Vcxyzxy

f

x y z dxdydz dy dx f x y z dz=

∫∫∫ ∫ ∫ ∫

.

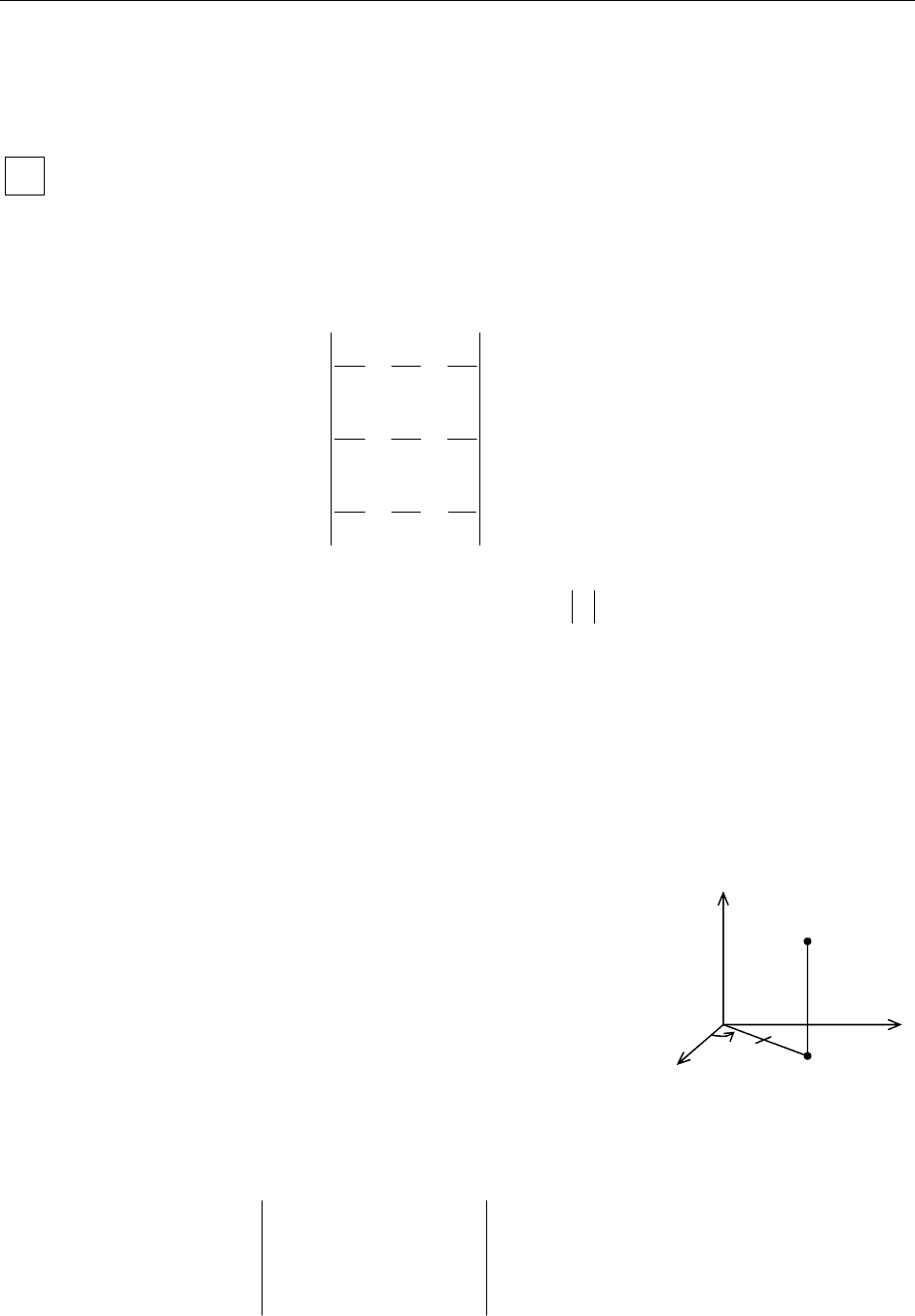
Пример:

Вычислите

G

x

yzdxdydz

∫∫∫

, где - пи-

рамида, ограниченная плоскостям

,

G

и

0x = 0y

=

, 0z = , 1

x

yz

+

+=.

Решение:

Плоскость

: ABC 1

x

yz++=. Проекция

области

V на плоскость

x

Oy есть

, ограниченный прямыми OAB∆ 0

=

x ,

, :

0=y

AB 1

x

y+=.

При

(, )

x

yD∈ аппликаты точек (,

x

,)yz V

∈

удовлетворяют неравенству

01zxy

≤

≤−−

.

()()

() () ()

1

11 11

2

00 0 00

0

11

2

00

1

11

234

24

00

0

2

1

[1 21 ]

2

11

121 1

22342234

xy

xx

G

x

z

xyzdxdydz xdx ydy zdz xdx ydy

xdx y x x y y dy

yyy

121

x

x x dx x x dx

−−

−

===

=−−−+=

⎡⎤

⎛⎞

=−−−+ =+−+

⎜⎟

⎢⎥

⎝⎠

⎣⎦

∫∫∫ ∫ ∫ ∫ ∫ ∫

∫∫

=

()() () ()

111

44

000

11

11 1 1 1

24 24

5

x

xdx xdx xdx

⎧

⎫

⎡⎤

=−−−= −−− =

⎨

⎬

⎣⎦

⎩⎭

∫∫∫

11

56

00

1(1) (1) 111 1

24 5 6 24 5 6 720

xx

==

⎡⎤

−−

⎛⎞

⎢⎥

=− + = −=

⎜⎟

⎝⎠

⎢⎥

⎣⎦

.

0

D

V

)0,0,1(A

)0,1,0(B

x

y

)1,0,0(C

z

0

y

)1,0(

)0,1(

1

=

+ yx

x

xyx

−

≤

≤∈ 10],1,0[

!

Лекция 1 - 4

28

3.2. Замена переменных в тройном интеграле

Цель: упростить вычисление интеграла.

Если функции ( , ,), (, ,), ( , ,)

x

xuvt y yuvt z zuvt=== являются непрерывно

дифференцируемыми и взаимно однозначно отображают точки про-

странства на точки пространства ,,uvt ,,

x

yz и наоборот и якобиан пе-

рехода, численно равный определителю третьего порядка, не равен ну-

лю

x

xx

uvt

yyy

J

uvt

zzz

uvt

∂∂∂

=

∂∂∂

,

то при замене переменных в тройном интеграле справедлива формула

(

)

(

)

,, ,,

dV

GG

f

x y z dV f u v t J dudvdt

∗

′

=

∫∫∫ ∫∫∫





.

Частным случаем преобразования координат является переход от декартовых

координат к цилиндрическим и сферическим координатам.

3.3.Тройной интеграл в цилиндрических координатах

Цилиндрические координаты представляют

собой соединение полярных координат в плос-

кости

xOy с декартовой аппликатой z.

cos ,

sin ,

,

x

y

zz

ρ

ϕ

ρ

ϕ

=

⎧

⎪

=

⎨

⎪

=

⎩

0,

02,

.

z

ρ

ϕ

π

≤<∞

≤<

−∞ < < ∞

x

ϕ

0

ρ

),,( zM

ϕ

ρ

z

y

Т

Найдем якобиан перехода:

()

22

cos sin 0

, , sin cos 0 cos sin

001

Jz

ϕ

ρϕ

ρ

ϕϕρϕρϕρϕρ

−

⋅

=⋅=⋅+⋅=

;

(,,) ( cos , sin ,)

VV

f

x y z dxdydz f z d d dz

ρ

ϕρ ϕ ρ ρ ϕ

′

=

∫∫∫ ∫∫∫

.

Кратные интегралы

29

3.3.1. Элемент объема в цилиндрических координатах

Для вычисления элемента объема в цилин-

дрических координатах разобьем область

V ко-

ординатными поверхностями:

ϕ

=

ϕ

i

-

полуплоскости, проходящие через

Oz,

j

ρ

=

–

круговые цилиндры;

– плоскости, пер-

пендикулярные оси

. Элементарным объе-

мом будет криволинейная призма.

k

zz=

Oz

z

∆

x

y

ϕ

∆

ρ

∆

ϕ

ρ

Площадь основания с точностью до бесконечно малых высшего порядка рав-

на ()

ρ

ϕ

∆∆

ρ

; высота равна ∆ . Тогда z

Vz

ρ

ϕρ

∆ ≈ ⋅∆ ⋅∆ ⋅∆ , dV d d dz

ρ

ρϕ

= .

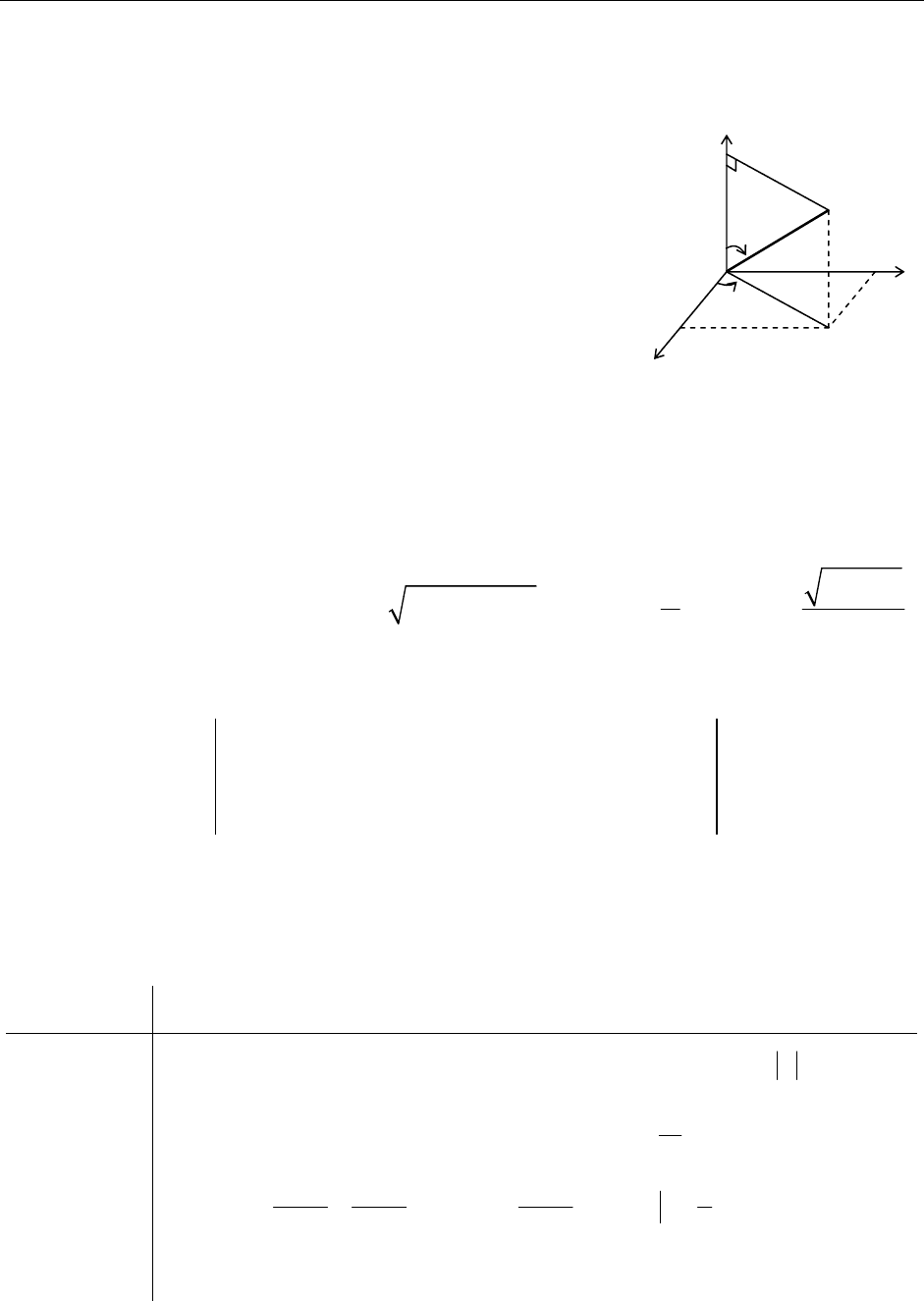
Пример:

Вычислите

22

V

zx y dxdydz+

∫∫∫

, где область

ограничена цилиндром

V

22

2

x

yx

+

= и плоскостями

.

0, 0,yzz≥==a

10y+−=

1

Решение:

Уравнение

,

представляет собой окружность с

22 22

2(1)xy xx+−=−

22

(1)xy−+=

1

=

R и центром в точке

. В полярных координатах

(1, 0)

2

2cos

ρ

ρϕ

= .

Пределы изменения новых переменных:

0 za

≤

≤ , 0

2

π

ϕ

≤

≤ ,

02cos

ρ

ϕ

≤≤

.

2

22 2

00 0

cos

a

VV

zx ydxdydz z dddz d d zdz

π

ϕ

ρρ ρϕ ϕ ρ ρ

′

+=⋅ =

∫∫∫ ∫∫∫ ∫ ∫ ∫

=

∫∫∫∫

=−===

2

0

22

2

0

32

2

0

cos2

0

22

)(sin)sin1(

3

4

cos

3

4

2

1

πππ

ϕ

ϕϕϕϕρρϕ

dadadda

2

0

3

2

9

8

3

sin

3

4

aa =

⎥

⎦

⎤

⎢

⎣

⎡

−=

π

ϕ

.

y

0

1

)(

ρ

x

Лекция 1 - 4

30

3.4. Тройной интеграл в сферических координатах

Положение точки

(

)

,,

M

xyz в пространстве

определяется тремя числами

x

A

0

ϕ

ρ

θ

y

B

z

),,(

ϕ

θ

ρ

M

,,.

θ

ρϕ

(

)

(

)

,, ,,Mxyz M

ρ

θϕ

→ . Сферические координа-

ты ,,

ρ

θϕ

:

ρ

– радиус-вектор , OM

θ

– угол

между радиус-вектором и осью

, Oz

ϕ

– угол

между проекцией

ρ

на плоскость xOy и осью Ox.

Сферические координаты связаны с декартовыми

следующими соотношениями:

0,

02,

ρ

θ

π

ϕ

π

≥

⎧

⎪

≤≤

⎨

⎪

≤≤

⎩

sin cos ,

sin sin ,

cos .

x

y

z

ρ

θϕ

ρ

θϕ

ρθ

=

⋅⋅

⎧

⎪

=⋅ ⋅

⎨

⎪

=⋅

⎩

,

22

arctg

x

y

z

θ

+

= .

При этом

22 22

sinxy

ρ

θ

+= ,

222

x

yz

ρ

=

++, arctg

y

x

ϕ

=

Якобиан перехода:

()

2

sin cos sin sin cos cos

, , sin sin sin cos cos sin sin .

cos 0 sin

J

θ

ϕρ θ ϕρ θ ϕ

ρ

ϕθ θϕρθϕρθϕρ

θρθ

⋅−⋅⋅ ⋅⋅

=⋅ ⋅⋅ ⋅⋅=⋅

−⋅

θ

(

)

(

)

2

,, ,, sin

VV

f

x y z dxdydz f d d d

ρ

θϕ ρ θ ρ ϕ θ

∗

′

=

∫∫∫ ∫∫∫

.

Пример:

Найти объем шара радиуса R.

шара

VV V

V dV dxdydz J d d d

ρ

ϕθ

′

=

== =

∫∫∫ ∫∫∫ ∫∫∫

22

3

22

000 00

sin sin sin

3

R

V

R

ddd d d d d d

ππ ππ

ρθρϕθ θθϕρρ θθϕ

′

== =

∫∫∫ ∫ ∫ ∫ ∫ ∫

=

()

33 3

3

0

00

22 2 4

sin sin cos .

33 3 3

RR R

dd

ππ

π

ππ π

θθ θθ θ π

===−=

∫∫

R

Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов

Подождите немного. Документ загружается.