Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов
Подождите немного. Документ загружается.

Теория поля
41
8.4. Физический смысл линейного интеграла
8.5. Ротор (вихрь) векторного поля
8.5.1. Свойства ротора (вихря)
8.6. Теорема Стокса
8.7. Инвариантное определение ротора
8.8. Физический смысл ротора
8.9. Формула Грина
9.1 Потенциальное векторное поле
9.1.1. Условия потенциальности поля
9.1.2. Вычисление потенциала поля
9.2 Соленоидальное поле
9.2.1. Свойства соленоидального поля
9.3 Операторы Гамильтона и Лапласа
9.3.1.
Оператор Гамильтона (набла)
9.3.2. Оператор Лапласа
5.1. Скалярное поле
Если с каждой точкой
(, ,)
P
xyz
некоторой пространственной области G
связана скалярная величина, то говорят, что в области G задано ска-
лярное поле:
, где
(, ,)ufxyz= (, ,)
f
xyz
- скалярная функция, назы-
ваемая функцией поля.
О
Примеры скалярных полей: поле температур, поле давления, поле плот-
ности, поле концентраций, поле электрического потенциала. Рассмотрим
подробнее последний пример.
Пусть речь идет о точечном заряде q. Потенциал электростатического
поля заряда q, помещенного в начало координат, задается в каждой точке
пространства
(, ,)rx
y
z
, за исключением начала координат, функцией поля
вида:
22
qq q
u
r
r
2
x
yz
== =
+
+
.
Заметим, что если
constr
=
, - уравнение сферы. Следо-
вательно, в точках, принадлежащих сфере, потенциал электростатического
поля сохраняет свое значение, или
222
constxyz++=
constu
=
.
Ограничимся рассмотрением так называемых стационарных полей, т.е.
полей, не зависящих от времени.
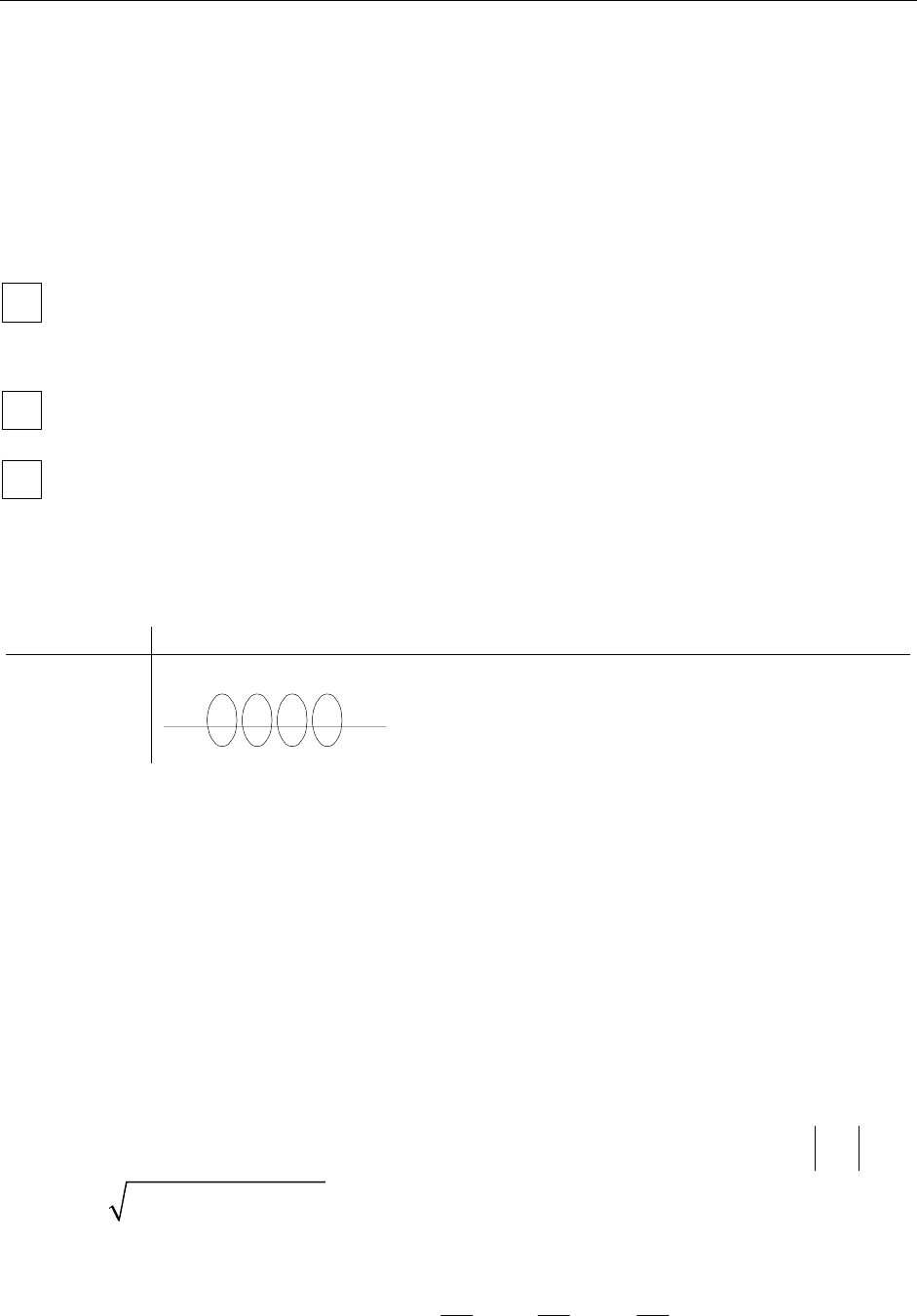
Лекция 5 - 9
42
5.2. Поверхности и линии уровня
В дальнейшем, если не оговорено особо, предполагаем функцию
однозначной и непрерывно-дифференцируемой.
(, ,)ufxyz=
Рассмотрим точки области, в которой функция
(, ,)ufxyz
=
принимает по-
стоянные значения:
(, ,) ,( const)
f
xyz c c
=
=
. Это уравнение можно рассмат-
ривать как уравнение некоторой поверхности в пространстве.
Геометрические места точек
(, ,)
P
xyz
, где скалярное поле принимает
одно и то же значение
(, ,)
f
xyz c
=
, называются поверхностями уровня
или эквипотенциальными поверхностями.
О
!
В силу однозначности функции
(, ,)ufxyz
=
поверхности уровня, соот-
ветствующие различным значениям c, не пересекаются между собой.
О
Скалярное поле называется плоским, если при подходящем выборе сис-
темы координат функция поля зависит только от двух переменных.
Множество точек плоскости
(, )
P
xy
, для которых
(, )
f
xy c=
, называет-
ся линией уровня плоского скалярного поля.
Пример:
Поле температур бесконечной равномерно нагретой нити.
линии уровня – окружности
5.3. Производная по направлению
Пусть в пространственной области G задано скалярное поле:
. Рассмотрим точку
(, ,) ( )uuxyz uP==
1
(, ,)
P
xyz
и исходящий из нее вектор
{
}
,,
x
yz
llll=
. Найдем, как изменяется поле в направлении вектора
l
. Сме-
стимся из точки
1
(, ,)
P
xyz
в направлении вектора в точку
. Обозначим за
l
2
(, ,Px xy yz z+∆ +∆ +∆ )
l
∆
длину вектора
12 12
:PP l PP∆=
, то-
гда
22
lxy∆= ∆ +∆ +∆
2
z
. При этом функция поля получит приращение
21
() () ( , , ) (,,)uuP uP ux xy yz z uxyz∆ = − = +∆ +∆ +∆ − =
12 3
()
uuu
du x y z x y z l
xyz
εε ε θ
∂
∂∂
= +∆+ ∆+ ∆= ∆+ ∆+ ∆+ ∆
∂∂∂
,

Теория поля
43
где
(l)
θ
∆
- бесконечно малая более высокого поряд-
ка по
,l∆
123
,, 0
ε
εε
→
при
,,
x
y∆∆
0z
∆
→
, а величи-
на
cp
u
V
l
∆
=
∆
- средняя скорость изменения скалярной
функции
в направлении вектора
l
()uP
.
x
1
P
2
P
l
y
123
uuxuyuz x y
lxlylzl l l
εεε
∆∂∆∂∆∂∆ ∆ ∆ ∆
=+++++
∆∂∆∂∆∂∆ ∆ ∆ ∆
z
l
.
Перейдем к пределу при
, что соответствует стремлению
0l∆→
21
P
P→
:
0
cos cos cos
lim
l
uu u u
lx y z
α
βγ
∆→
∆∂ ∂ ∂
=++
∆∂ ∂ ∂
,
где
cos
α
,
cos
β
,
cos
γ
- направляющие косинусы вектора . Поскольку
12
PP
12
PP l
, то их направляющие косинусы равны. Так как
x
yz
lliljlk=+ +
, то
cos
||
x
l
l
α
=
, cos
||
y
l
l
β
=
,
cos
||
z
l
l
γ
=
.
Производной функции u в точке
(, ,)
P
xyz
(обозначение
u
l
∂
∂
) по направ-
лению вектора
l
называется предел
0
lim
l
u
l
∆→
∆
∆
(если он существует), рав-
ный
0
cos cos cos
lim
l
uuu u u
llx y z
α
βγ
∆→
∂∆∂ ∂ ∂
== + +
∂∆∂ ∂ ∂
.
О
l
Производная
u
l
∂
∂
по направлению определяет скорость изменения ска-
лярного поля в направлении вектора
l
, в частности, если
u
l
∂
∂
>0, поле возрас-
тает, если
u
l
∂
∂
<0, поле убывает.
Пример:
Найти производную
u
l
∂
∂
в точке Р (1,1,1) в направлении вектора
kji ++=
, если.
22
ux y z=++
2
Решение:
22, 22, 22
xyz
PP P PP
P
ux uy uz
′′′
== == ==
;
3=
,
;
3
1
cos;
3
1
cos;
3
1
cos
γβα
==
1116
222
3333
u
0
∂
=
++=>
∂
,
следовательно, скалярное поле возрастает.
Лекция 5 - 9
44
5.4. Градиент скалярного поля
Пусть задано скалярное поле
u=(x,y,z).
Градиентом скалярного поля u в точке
(, ,)
P
xyz
называется вектор,
обозначаемый символом
и определяемый равенством
grad u
О
uu u
grad u i j k
x
yz
∂
∂∂
=+ +
∂
∂∂
,
5.4.1. Оператор Гамильтона (набла)
Введем символический вектор “набла” или оператор Гамильтона
;;ijk
x
yzxyz
⎛⎞
∂∂∂∂∂∂
∇= + + =
⎜⎟
∂∂∂∂∂∂
⎝⎠
.
Знак
используется для записи операций векторного анализа в сокра-
щенной и удобной для расчётов форме.
∇
!
Выражение вида
(, ,)ux
y
z∇
понимается как результат действия опера-
тора на соответствующую функцию.
Тогда
(, ,) ( ) (, ,)
x
yz
uu u
uxyz i j k uxyz i j k ui u j uk
xyz xyz
∂∂∂ ∂∂∂
′′ ′
∇=++⋅ =++=++
∂∂∂ ∂∂∂
,
g
rad u u
=
∇
.
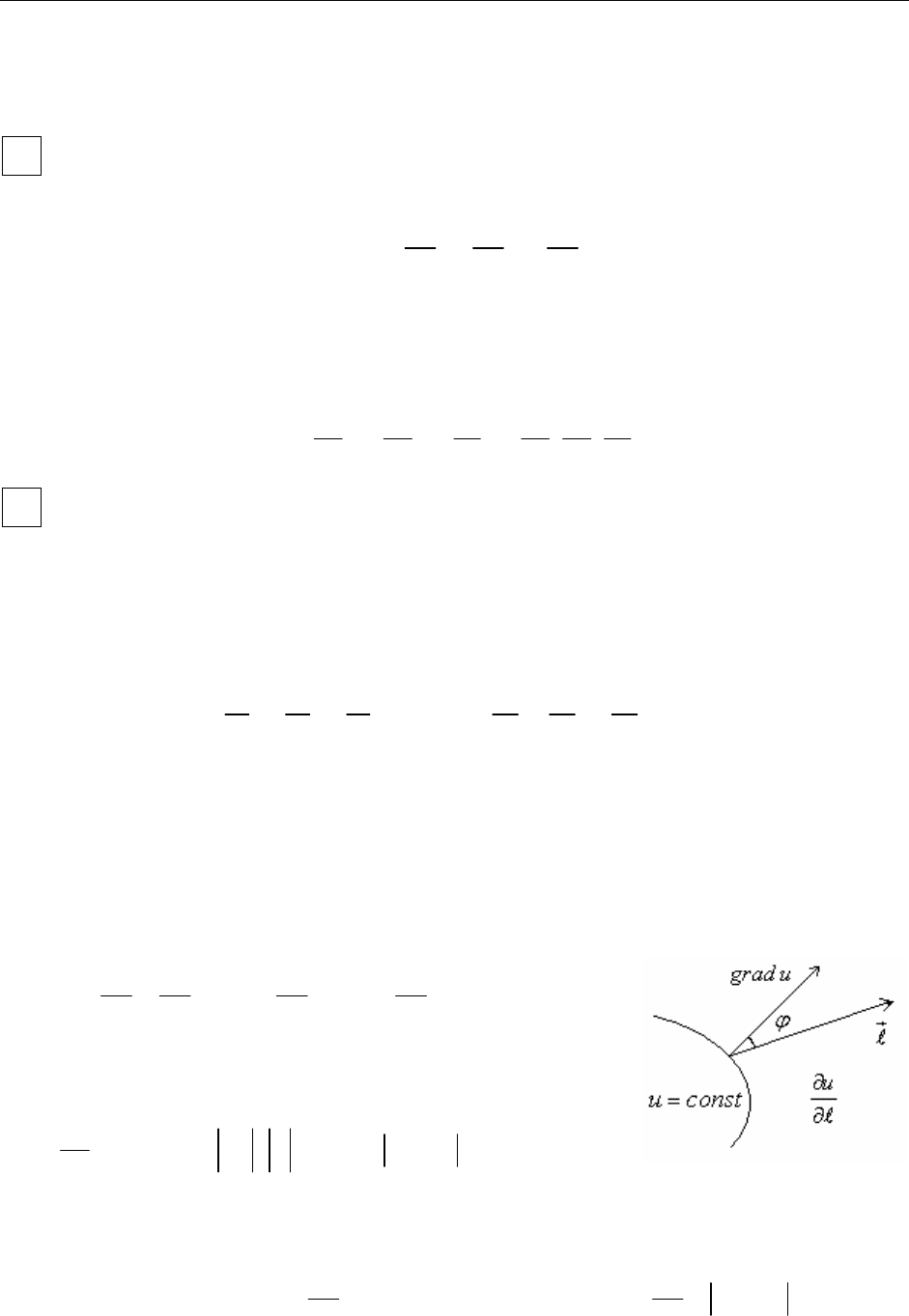
5.4.2. Связь производной по направлению с градиентом
cos
uu
cos cos
u u
xyz
α
βγ
∂ ∂
=++
∂ ∂
∂∂
∂∂
.
Пусть
l
0
(cos ,cos ,cos )
α
βγ
=
- единичный
вектор (орт) в направлении
l
, тогда видно, что
00
cos cos
u l grad u
()
u
u l
ϕ
ϕ
=∇ ⋅ ⋅ = ⋅
∂
=∇⋅
∂
,
где
ϕ
- угол между единичным вектором
0
l
данного направления и векто-
ром градиента
.
l
grad u
Если
0grad u
=
, то 0
u
l
∂
=
∂
. Если
0grad u
≠
, то
u
grad u
l
∂
<
∂
для всех
векторов
, за исключением вектора
l
l
, направленного в сторону .
grad u

Теория поля
45
Вывод: cos
u
grad u
l
ϕ
∂
=⋅
∂
. Производная по направлению вектора
l
в
точке
(, ,)
P
xyz
равна проекции градиента на данное направление.
5.4.3. Свойства градиента
Пусть задан градиент поля и производная по направлению:
,,
uuu
u
x
yz
⎧⎫
∂∂∂
∇=
⎨
∂∂∂
⎩⎭
⎬
,
u∇
=
2
2
2
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
z
u
y
u
x
u
.
1. Максимальное значение производной по направлению равно модулю
градиента:
cos
u
gradu
l
ϕ
∂
=⋅
∂
;
0;cos 1
ϕ
ϕ
→→⇒
max
u
grad u
l
∂
=
∂
.
2. Вектор
направлен в сторону возрастания поля.
u∇
3. Вектор
всегда нормален к поверхности (линии) уровня поля (экви-
потенциальной поверхности).
u∇
Доказательство:
Пусть
скалярное поле и
(, ,)uuxyz= czyxu
=
),,(
- уравнение поверх-
ности уровня. Выберем
{
czyxuP
}
=
∈∀ ),,(
, которую обозначим
(, ,)Pxyz
, и
проведём касательную плоскость к поверхности, описываемой уравнением
(, ,) (, ,) 0Fxyz uxyz c
=
−=
;
() ( ) ()
FF F
xx yy zz
xy z
∂∂∂
−+ −+ −=
∂∂ ∂
0
- уравнение касательной плоскости;
() ( ) ()
uu u
xx yy zz
xy z
0
∂
∂∂
−+ −+ −=
∂∂∂
.
Тогда вектор нормали касательной плоскости имеет вид:
,,
uuu
n
x
yz
⎧
⎫
∂∂∂
=
⎨
⎬
∂∂∂
⎩⎭
,
uu u
ni jk
xy z
u
∂
∂∂
=
++=∇
∂∂ ∂
.
!
Свойства 1-3 дают
инвариантное (не зависящее от системы координат)
определение градиента, т.е. утверждают, что независимо от системы ко-
ординат
указывает величину и направление наибольшего возраста-
ния скалярного поля в точке:
u∇
u
grad u mах
l
∂
⎛⎞
=
⎜⎟
∂
⎝⎠
.
Лекция 5 - 9
46
Дифференциальные свойства градиента:
Если скалярное поле есть сумма двух полей:
(,,) (,,) (,,)
f
xyz uxyz vxyz=+
, то
()
f
uv u v
∇
=∇ + =∇ +∇
.
.
()() (uv uv u v∇⋅=∇ +∇
)
.
cu c u∇⋅ =∇
()
u
f
uf
′
∇=⋅∇
u
- градиент сложной функции.
(,)
uv
f
uv f u f v
′′
∇=⋅∇+⋅
∇
.
Пример:
Найти наибольшую крутизну подъёма поверхности
в точке
Р (2,2,4).
y
xu =
Решение:
u
grad u mах
l
∂
⎛⎞
=
⎜⎟
∂
⎝⎠
.
u∇=
x
yz
ui u j uk
′′ ′
++
=
1
0
yy
yx i x ln x j k
−
+
+
.
12 2 2 2 2
( ) ( ln ) (2 2) (4ln 2) 4 1 ln 2
yy
uyx xx
−
∇= + = ⋅ + = +
.
Пример:
Найти нормаль к поверхности
в точке Р (1,1,1).
222
zyxu ++=
Решение:
По свойству 3:
nu
∇
,
22 2uxi
yj
zk∇= + +
,
()
()
1,1,1
1,1,1
22 2
P
P
uxiyjzk∇=++ =
22 2ij
k
+
+
⇒
{
}
111
,,
0
333
n =
. =
{
}
2, 2, 2
Пример:
Найти градиент функции
2
0
2
0
2
0
)()()( zzyyxxr −+−+−=
(модуль радиус-вектора).
Решение:
P
0
-фиксированная точка, P(x,y,z) – изучаемая точка поверхности.
g
rad r =
k
z
r
j
y
r
i
x
r
∂
∂
+
∂
∂
+
∂
∂
=
{
}
000
222
000
;;
()( )()
xxyyzz
x
xyyzz
−−−
−+−+−
0
=
r
- единичный вектор, параллельный вектору
0
P
P
.
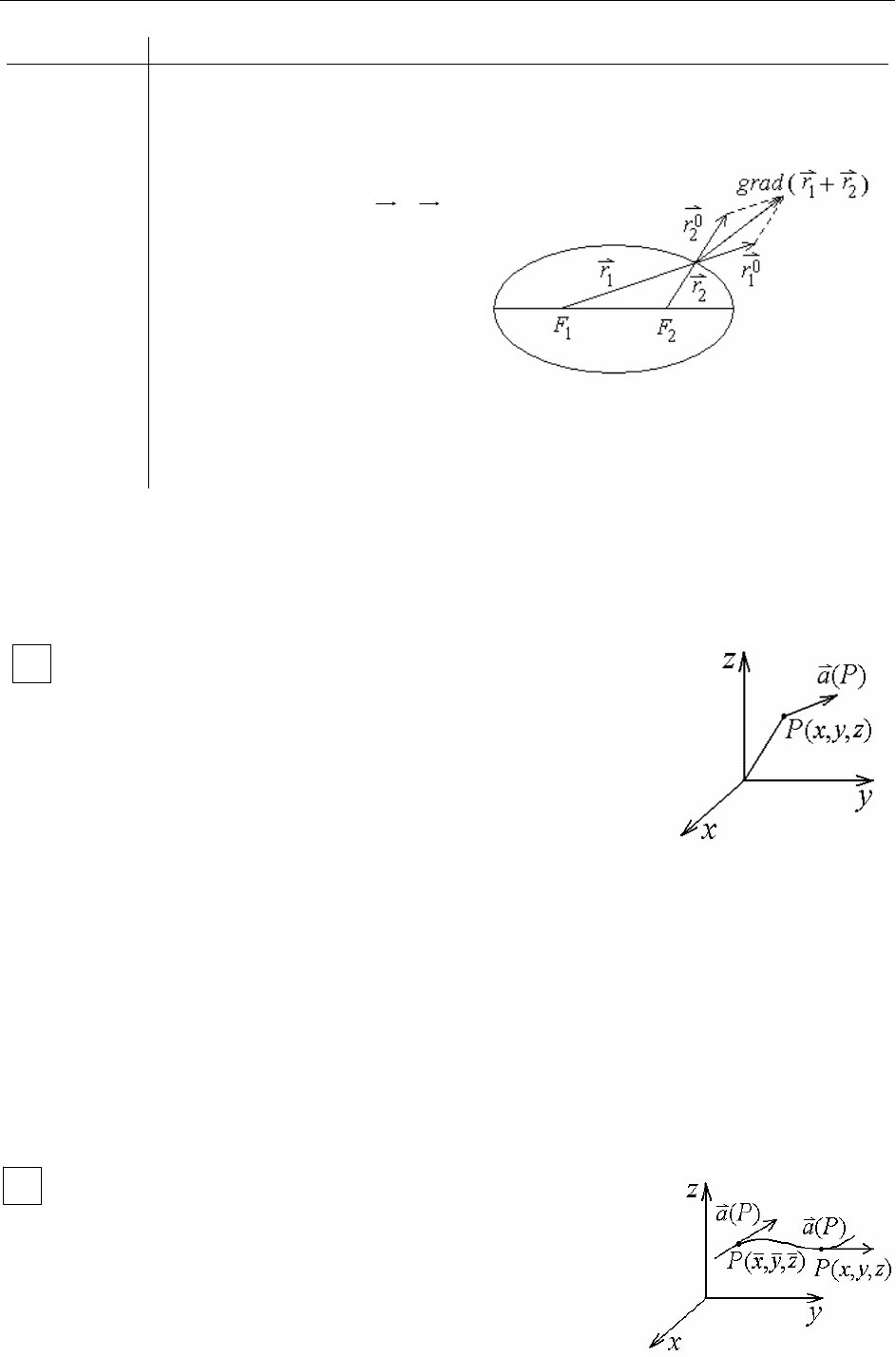
Теория поля
47
Пример:
Найти градиент скалярной функции
(
)
1
uP r r
2
=
+
, где , - расстояния
от точки Р до фиксированных точек
1
r
2
r
1
F
,
2
F
. Линии уровня этой функции
– эллипсы.
Решение:
Имеем:
0
2
0
121
)( rrrrgrad +=+
,
т.е. градиент равен диагонали
ромба, построенного на ортах
радиус-векторов, проведенных
к точке Р из фокусов
1
F
и
2
F
.
Нормаль к эллипсу в какой-
либо точке делит пополам угол
между радиус-векторами, проведёнными в эту точку.
Физическая интерпретация: луч света, вышедший из одного фокуса, по-
падает в другой фокус.
5.5. Векторное поле
Если с каждой точкой
(; ;)
P
xyz
пространственной
области
G связана векторная функция её радиус-
вектора
, то говорят, что в области G за-
дано векторное поле.
()
aaP=
О
Векторное поле определяется тремя скаляр-
ными характеристика вектора ми – координатами
a
,
{
}
,,
x
yz
aaaa=
или
x
yz
aaiajak=+ +
, где
(, ,)
xx
aaxyz
=
, ,
- проекции векторного поля на оси координат или компоненты
вектор-функции. Будем считать, что они непрерывны и дифференцируемы по
всем переменным.
(, ,)
yy
aaxyz=
(, ,)
zz
aaxyz=
5.5.1. Векторные линии
Векторное поле можно изобразить графически, указав положение векто-
ра
в некоторых точках.
a
Векторной линией поля
(
)
aaP=
в области G
называется кривая, в каждой точке которой век-
тор
направлен по касательной к этой кривой.
a
О
Найдём уравнения векторных линий.
Предположим, что векторные линии есть прямые, то-
гда их уравнения:

Лекция 5 - 9
48
x
x
x
a
−
=
y
yy
a
−
=
z
zz
a
−
,
x
yz
x
yz
aaa
∆
∆∆
==
.
Так как любую кривую можно на бесконечно малом участке величины
заменить отрезком касательной, а направление касательной
совпадает с направлением
, то уравнения векторной линии имеют вид:
(;;)dr dx dy dz=
a
x
yz
dx dy dz
aaa
=
=
.
На самом деле речь идет о системе дифференциальных уравнений первого
порядка.
;;
y
.
z
z
x
xy
a
dy dz a dz a
dx a dx a dy a
===
Общее решение этой системы:
определяет двухпараметриче-
ское семейство линий и дает совокупность всех векторных линий поля.
1
22
(, ,) ;
(, ,) ,
xyz C
xyz C
ϕ
ϕ
=
⎧
⎨
=
⎩
1
Векторной трубкой называется совокупность всех
векторных линий, пересекающих часть некоторой
лежащей в векторном поле поверхности
Σ
, ограни-
ченной замкнутым контуром
Γ
.
О
5.5.2. Плоское векторное поле
О
Векторное поле называется плоским, если все
векторы лежат в параллельных плоскостях.
Уравнение векторных линий
0
xy
dx dy dz
aa
==
.
!
В плоском поле векторные линии есть плоские
кривые
(
)
yx
ϕ
=
.
Теория поля
49
Пример:
Найти векторные линии поля, если поле задано вектором
kbjxiya
++−=
в точке Р (1,0,0)
Решение:
b
dz
x
dy
y
dx
==
−
.
1).
x
dy
y
dx
=
−
,
,
ydyxdx −= 0
=
+
ydyxdx
;
22
2
1
22
xy
c+=
;
22
21
2;ccxy=+
2
2
c=
- уравнение окружности.
2).
b
dz
x
dy
=
,
bdy
,
xdz=
2
2
cos ,
sin ,
x
ct
yc t
=
⎧
⎨
=
⎩
22
cos cosbc tdt c tdz=
,
dz bdt
=
,
1
2
2
,
cos ,
sin .
zbtc
x
ct
yc t
=+
⎧
⎪
=
⎨
⎪
=
⎩
В точке P (1,0,0):
2
1
1,
00,
00
c
c
=
⎧
⎪
=⇒
⎨
⎪
=+
⎩
2
1
1
0
c,
c.
=
⎧
⎨
=
⎩
Уравнение винтовой линии имеет вид:
cos
sin
x
t,
yt
zbt.
=
⎧
⎪
=
⎨
⎪
=
⎩
,
.
6.1. Односторонние и двусторонние поверхности
Рассмотрим гладкую и незамкнутую поверхность
∑
, ограниченную ку-
сочно-гладким контуром
γ
. Это означает, что для уравнения поверхности
существуют частные производные по всем переменным. В точке
Р проведём
нормаль
к поверхности. Через точку P проведем замкнутый контур Г, не
имеющий общих точек с границей
n
γ
.

Лекция 5 - 9
50
При обходе контура возможны две ситуации:
а) нормаль к поверхности
n
при возвращении в
точку
P сохранит свое направление;
б) при непрерывном движении вдоль замкнуто-
го контура
Г, непрерывно меняясь по направлению,
нормаль изменит направление на противоположное
при возвращении в исходную точку.
В случае «а» поверхность называется
двусто-
ронней
, в случае «б» – односторонней. Совокуп-
ность точек поверхности с определенным направле-
нием нормали
называется стороной поверхности.
n
!
Классическим примером односторонней поверхности является лист Ме-
биуса.
6.2. Площадь поверхности
Пусть
- незамкнутая гладкая поверхность. Разобьем ее на участки
, ( ), с помощью сети кривых. Выберем в каждом участке
Σ
i
∆Σ
1,...,i= n
i
∆
Σ
точку
. Проведем в точке касательную плоскость к поверхности
i
P
i
P
Σ
и
спроектируем
на касательную плоскость. На проекции получим плоскую
фигуру с площадью
.
i
∆Σ
i
S
′
∆
i
S
′
∆
О
Площадью поверхности
называется предел суммы площадей
S
(
), при условии, что диаметры всех частей разбиения
1,...,i= n
i
∆
Σ
стремятся к нулю:
0
1
lim
i
n
i
i
SS
∆Σ →
=
′
=∆
∑
.
!
Поверхность, имеющая площадь, называется
квадрируемой.
Пусть поверхность задается явным уравнением
(
)
,
z
zxy
=
, где
(
)
,
z
xy
-
непрерывно дифференцируемая функция, и однозначно проектируется в
плоскую область
x
y
D
на координатной плоскости . Нормаль
Oxy
n
к
поверхности
, как вектор, ортогональный к касательной плоскости, имеет
компоненты:
Σ
,,1
zz
n
xy
⎧
⎫
∂∂
=−
⎨
⎬
∂∂
⎩⎭
, и направляющие косинусы нормали равны:
n
(
)
2
2
cos , cos
1
z
x
ni
zz
x
y
α
∂
∂
==±
⎛⎞
∂∂
⎛⎞
++
⎜⎟
⎜⎟
∂∂
⎝⎠
⎝⎠
,
