Смольников А.П. Теория автоматического управления
Подождите немного. Документ загружается.

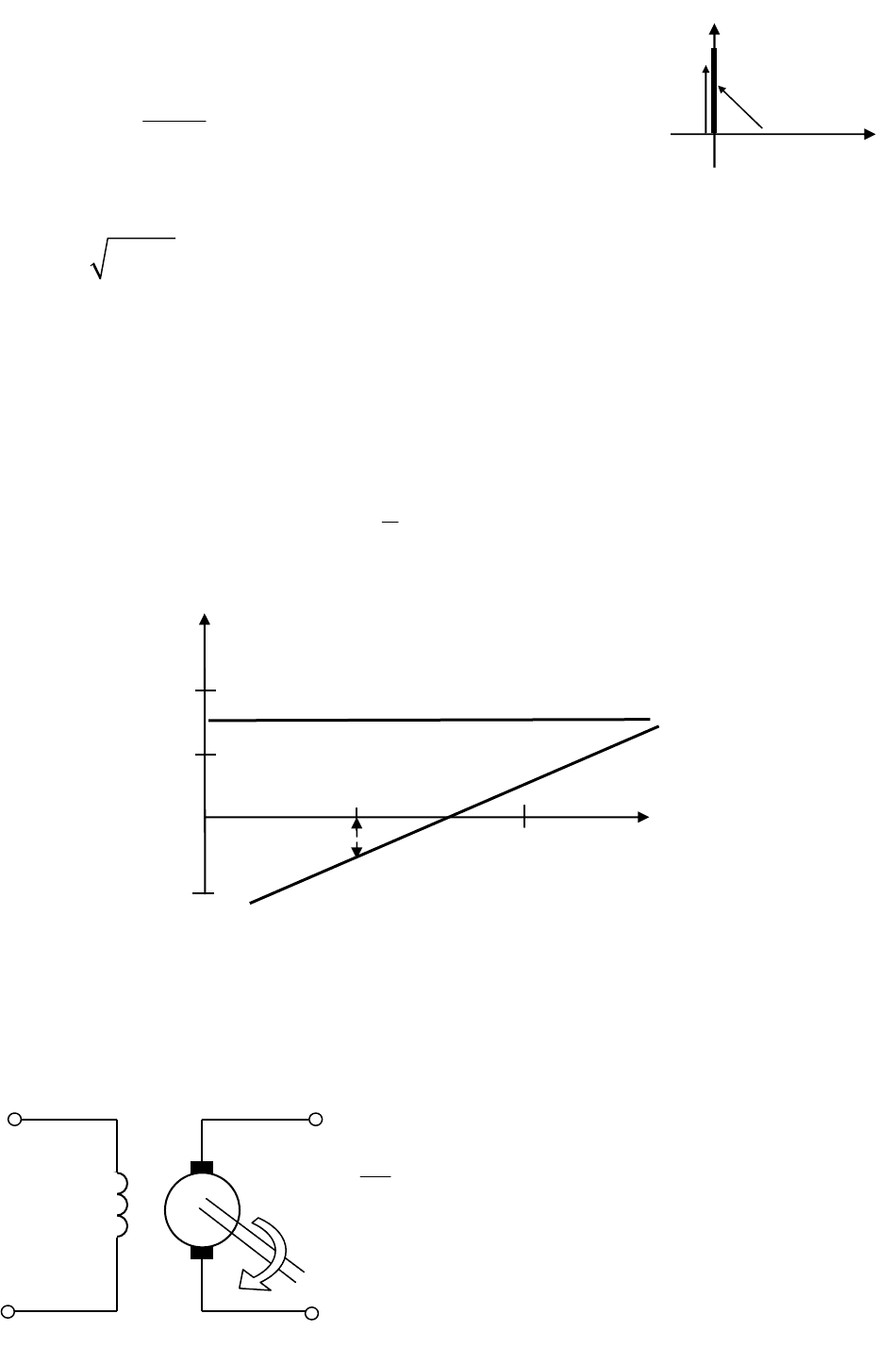
53
и изображена на рис. 4.49.
Частотная передаточная функция
ω
ω
k
j
j
W
=)( , тогда U(ω)=0; V(ω)=kω.
°=∞== 90
)(
)(
)( arctg
U
V
arctg
ω
ω
ωϕ
Построим ЛЧХ.
Найдем наклон ЛАХ
20lg 20lg10 (20lg 20lg ) 20 /kkдБ дек
ω
ω
+−+=+
1)
ω=1:
k
L
lg20)( =
ω
2)
ω
ω
k
L
lg200)( ==
k
1
=
ω
Логарифмические частотные характеристики приведены на рис. 4.51.
Примером звена является тахогенератор постоянного тока (рис. 4.52) в
режиме холостого хода (I
я
=0). При этом в качестве входной величины
рассматривается угол поворота якоря, а в качестве выходной – э.д.с. якоря e.
Приближенно в качестве
идеального дифференциального
звена может рассматриваться
x
2
=e=
dt
d
K
α
U
в
α
=
x
1
Рис. 4.52
ϕ
(
ω
)
ω=1/К
+20дБ/дек
L
(
ω
)
10
+90°
20l
gK
ω=1
ω
,
с
-1
ϕ
40
20
L,дБ
Рис. 4.51
ω→∞
ω
ϕ=90°
ω→0
U
V
Рис. 4.50
2
() ( )
() 20lg
A
kk
Lk
ω
ωω
ωω
==
=
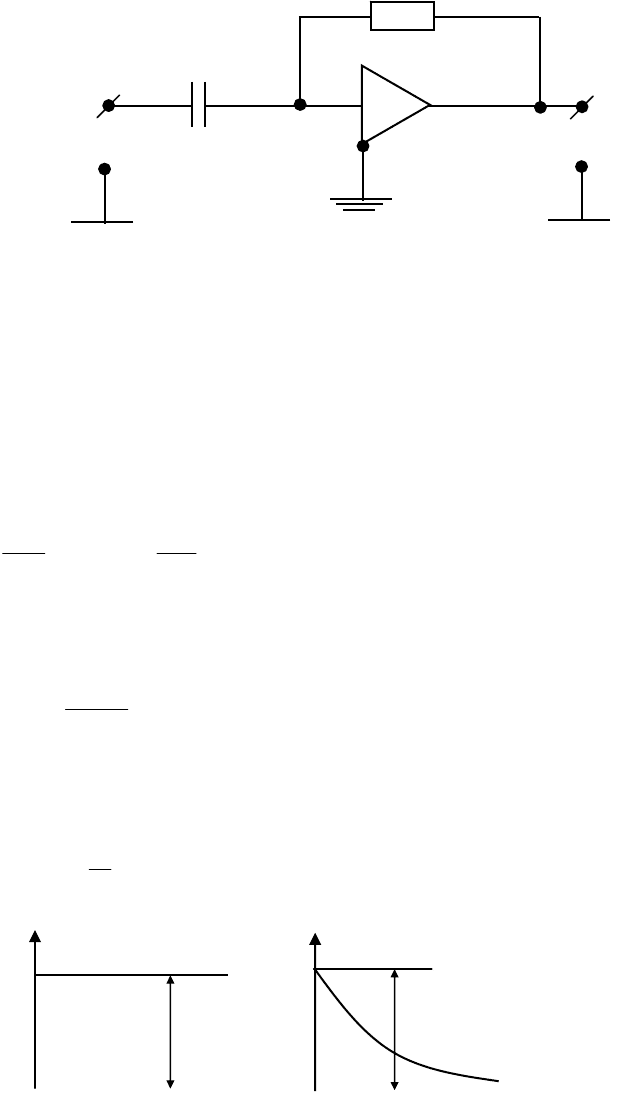
54
операционный усилитель в режиме
дифференцирования.
Необходимо отметить, что осуще-
ствить дифференцирование сигнала
в реальных системах довольно
сложно из-за наличия помех.
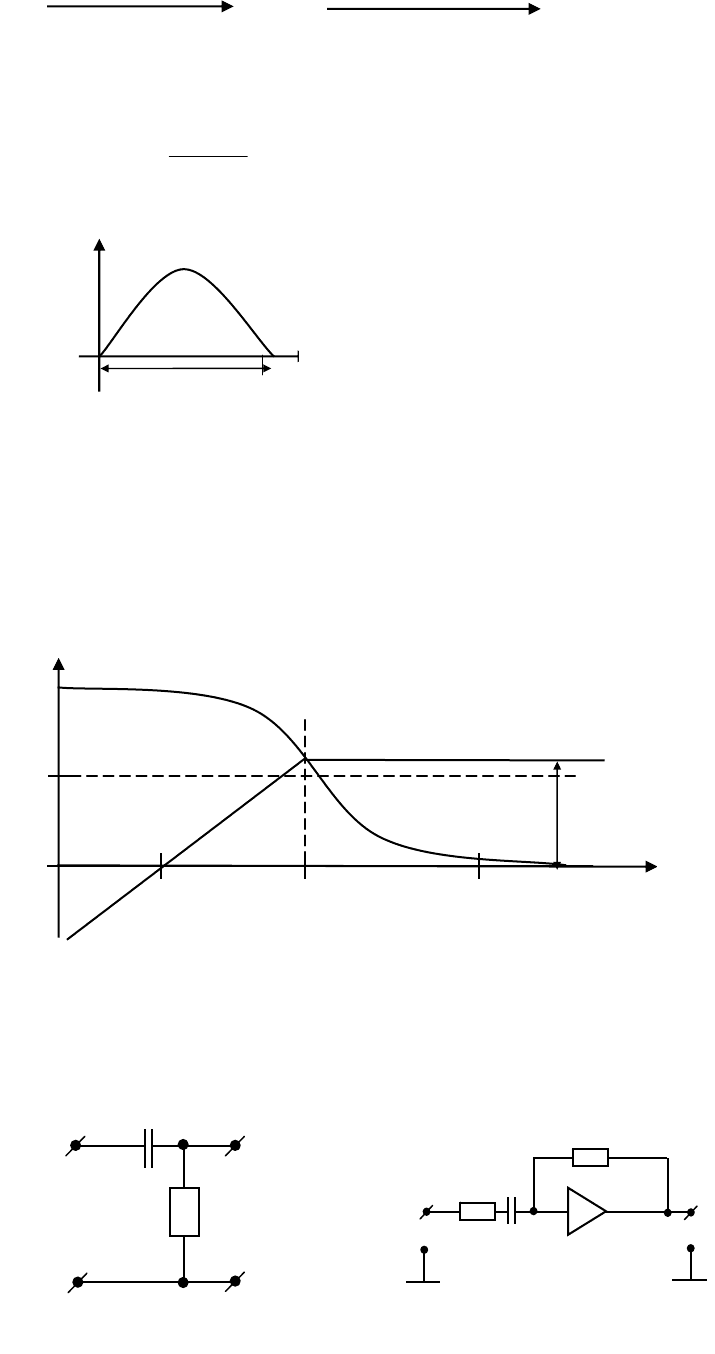
Приближенно в качестве идеального дифференциального звена может
рассматриваться операционный усилитель в режиме дифференцирования
(рис. 4.53).
Необходимо отметить, что осуществить дифференцирование сигнала в
реальных системах довольно сложно. Если x
1
(t) имеет разрывы первого рода,
то получение точной производной невозможно.
4.5.1. Дифференцирующее звено с замедлением
Описывается уравнением
21
2
dx dx
TxkT
dt dt
+=
Передаточная функция
1
)(
+
=
Tp
kTp
pW
Переходная функция (рис. 4.55)
T
t
keth
−
=)(
k
x
1
1
t
x
2
t
С
U
1
=x
1
U
2
=x
2
R
Рис. 4.53
55
Частотные характеристики
1
)(
+
=
ω
ω
ω
Tj
kTj
jW
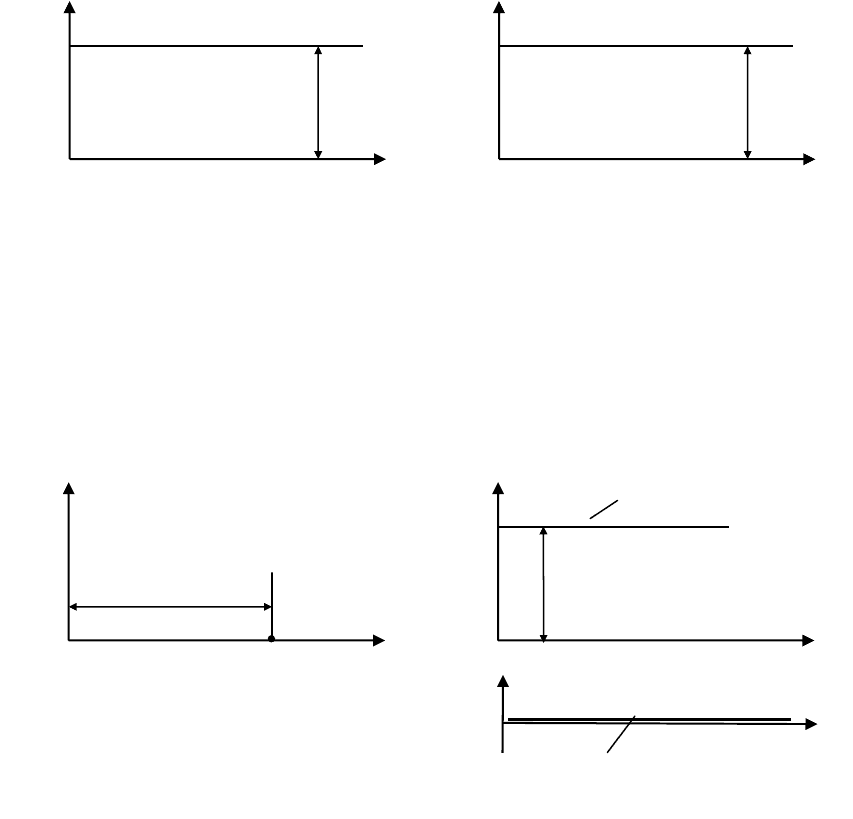
Логарифмические частотные характеристики (рис. 4.57).
Примеры:
Рис. 4.55
Рис. 4.54
ω=0
ω=∞
U
V
k
Рис. 4.56
20lgk
+20
+45°
ω,с
-1
1/T
ϕ(ω)
L(ω)
+90°
1 10
Рис. 4.57
R
С
U
1
=
x
1
U
2
=
x
2
Рис. 4.58
Рис. 4.59

56
1
1
z
Cp
=
22
zR=
2
21 1 1
12
1
1
zRRCp
UU U U
zz RCp
R
Cp
== =
++
+
11 +
=
+
=
Tp
Tp
RCp
RCp
W
, k=1.
Выше рассмотрены типовые линейные звенья, которые наиболее часто
встречаются в системах управления, но в некоторых САУ встречаются и
другие типы звеньев, например:
1) неминимально-фазовые устойчивые звенья (имеют нули в правой
полуплоскости),
2) неустойчивые звенья (имеют полюсы в правой полуплоскости)
1
)(
−
=
Tp
k
pW
,
3) звенья с распределенными параметрами, которые делятся на:
• иррациональные и описываются иррациональными функциями;
p
k
pW =)(
; ()
1
k
Wp
p
T
=
+
;
• трансцендентные, описываемые трансцендентными функциями;
например,
τ
p
epW
−
=)(
- звено чистого запаздывания.
4. ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ
Любую САУ можно разделить на ряд элементов, которые описываются
определенными дифференциальными уравнениями. Причем одним классом
дифференциальных уравнений могут описываться элементы различной
физической природы (электрические, механические, тепловые и т.д.). Этот
факт позволяет все многообразие элементов систем изучать на основе
ограниченного числа типовых динамических звеньев.
Поэтому класификация звеньев осуществляется именно по
типу
дифференциального уравнения или по виду передаточной функции.
Для каждого звена будем рассматривать следующие характеристики:
1. дифференциальное уравнение,
2. передаточная функция – W(p);
57
3. переходная функция – h(t);
4. частотные характеристики: W(j
ω
), L(
ω
),
ϕ
(
ω
);
5. примеры.
4.1. Безынерционное или пропорциональное звено
Описывается в статике и динамике уравнением
x
2
= Kx
1
,
где K - коэффициент усиления или передачи звена.
Передаточная функция имеет вид
W(p) = K.
Переходная функция звена
K
t
K
t
h
=
×
=
)(1)( .
Частотнвя передаточная функция имеет вид
W(j
ω) = K.
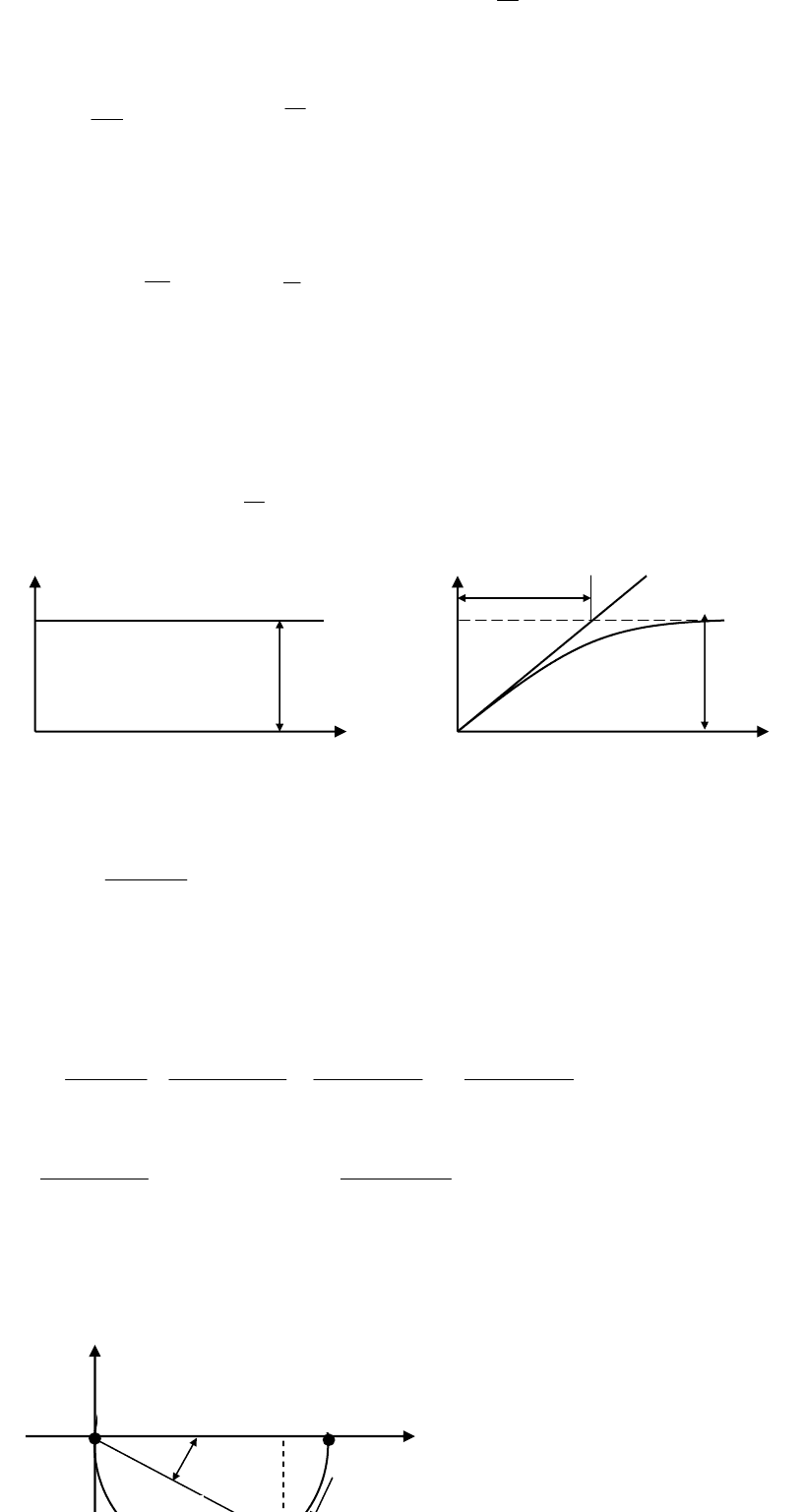
Характеристики изображены на рис. 4.3 – 4.5.
Примеры звеньев.
x
1
1
t
x
2
K
t
h(t)
Рис. 4.1
Рис. 4.2
0°
L(ω)=20lgK
V(ω)
K
U(ω)
Рис. 4.3 АФХ
20lgK
ω
L(ω)
ω
ϕ(ω)
ϕ(ω)=0°
Рис. 4.4. ЛАЧХ
Рис. 4.5. ЛФЧХ
58
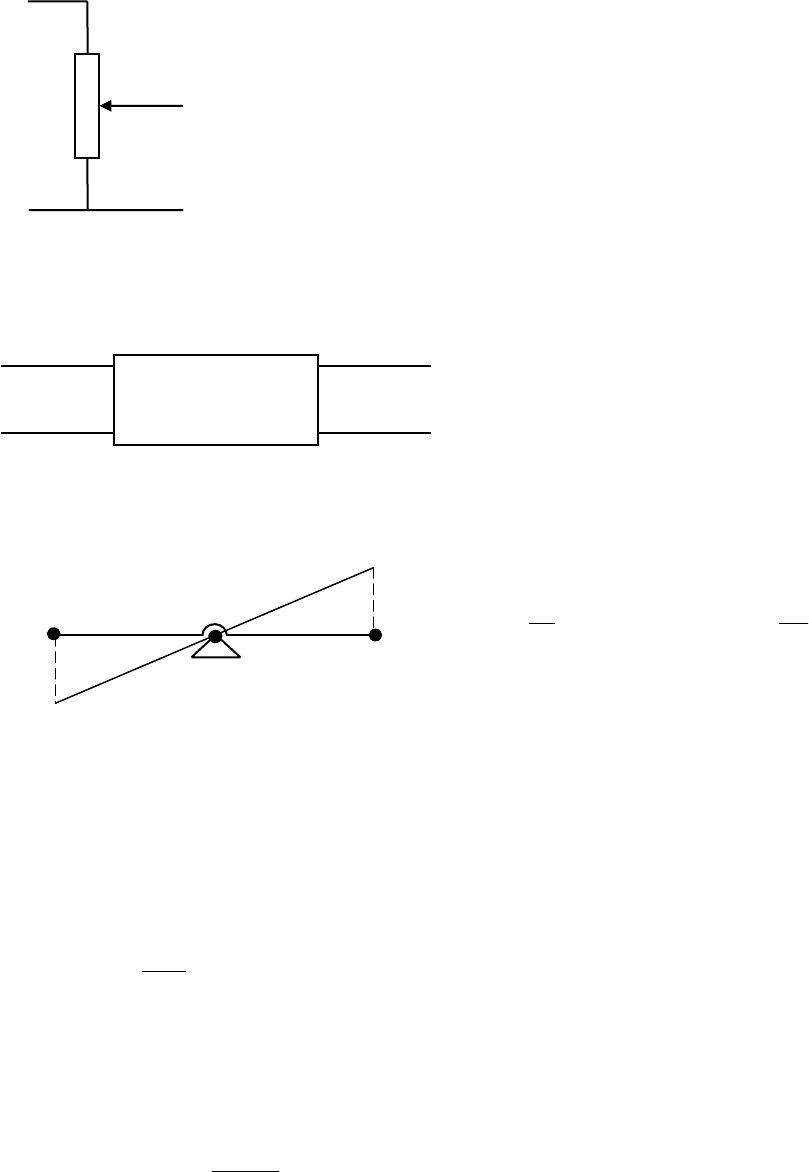
1) Делитель напряжения.
2) Электронный усилитель
3) Механический рычаг. Если пренебречь массой рычага, то
11
1
2
2
Kxx
l
l
x =⋅=
, где
1
2
l
l
K =
4.2. Апериодическое звено первого порядка
Описывается уравнением
2
21
dx
Txkx
dt
+=
;
где: k – коэффициент усиления, T – постоянная времени.
Передаточная функция
1
)(
+
=
Tp
k
pW
.
Найдем переходную функцию звена, решив дифференциальное
уравнение. Характеристическое уравнение имеет вид
01=+T
r
;
U
вых
R
1
R
2
U
вх
Рис
.
Рис.
47
Электронный
усилитель
U
вых
U
вх
U
вых
= K U
вх
U
ВЫХ
= K U
ВХ
,
K= R
2
/(R
1
+R
2
).
Рис.
48
l
1
l
2
x
2
x
1
59
Откуда единственный корень
T
r
1
−= .
Тогда общее решение дифференциального уравнения
T
t
Ce
rt
Cex
−
==
2
.
Если
1
() 1()xt t= , то частное решение
2
xk
∗
=
.
Тогда
222
*
t
T
x
xxCe k
−
=+= +;
Подставив начальные условия: t = 0, x
2
= 0, получим x
2
(0) = С + k = 0,
откуда C = – k.
Окончательное выражение для переходной функции (рис. 4.10) примет
вид
2
() (1 )
t
T
xhtk e
−
==− .
Частотная передаточная функция
Ее можно представить
1
22
1
22
)1(
)1(
1
)(
+
−
+
=
+−
+−
×
+
=
ω
ω
ω
ω
ω
ω
ω
T
kT
j
T
k
Tj
T
j
Tj
k
jW
;
;
1
22
)(
+
=
ω
ω
T
k
U
;
1
22
)(
+
−=
ω
ω
ω
T
k
T
V
Годограф изображен на рис. 4.11.
x
1
1
t
x
2
K
t
h(t)
T
Ри Рис.
410
1
)(
+
=
ω
ω
Tj
k
jW
V
ω=0
ω→∞
ϕ(ω
1)
A
(
ω
U
U(ω
1)
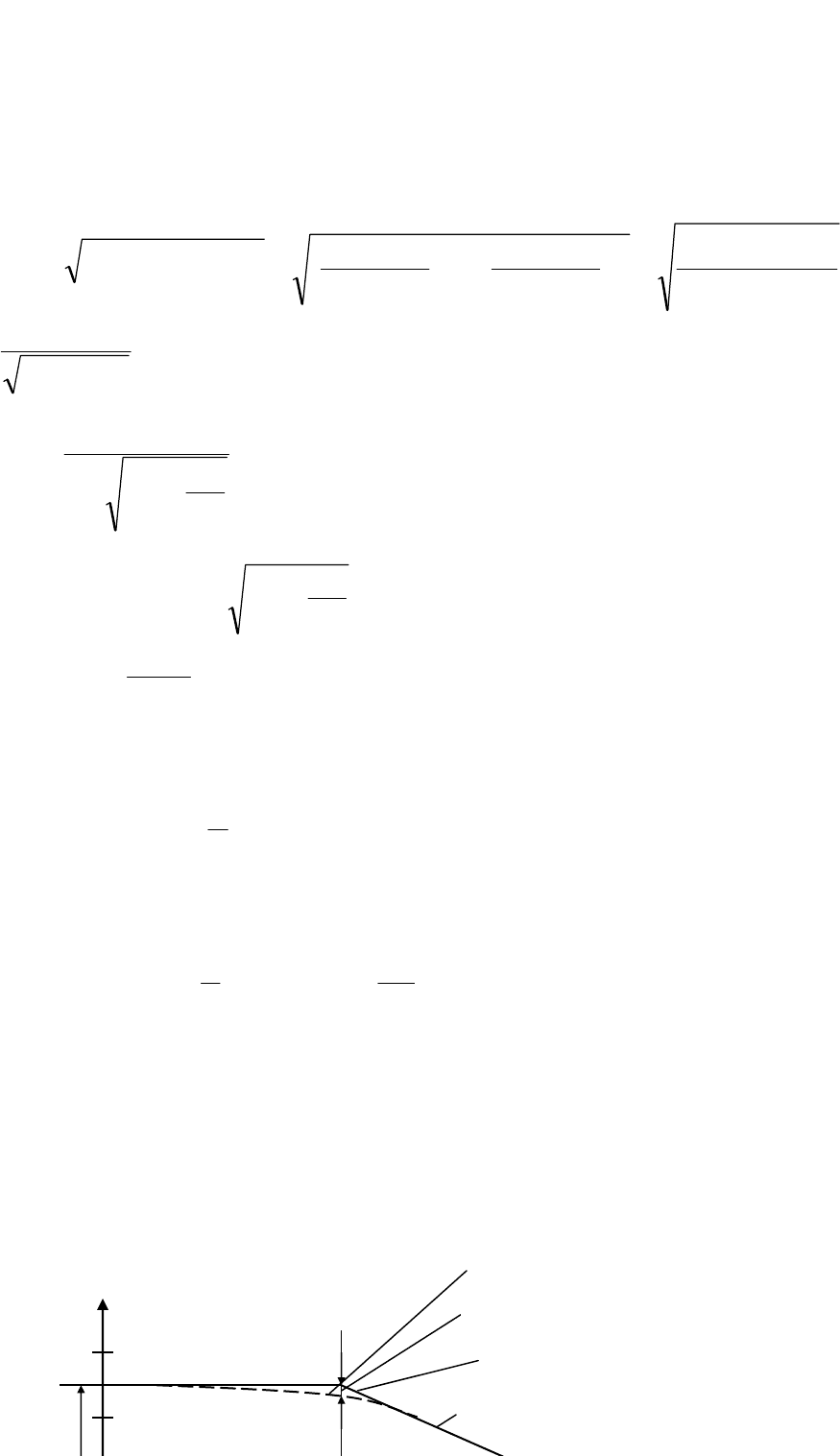
60
1
22
2
)1
22
(
)1
22
(
2
2
)
1
22
(
2
)
1
22
()(
2
)(
2
)(
+
=
=
+
+
=
+
+
+
=+=
ω
ω
ω
ω
ω
ω
ωωω
T
k
T
Tk
T
kT
T
k
VUA
;
2
1
2
)(
T
T
k
A
+×
=
ω
ω
;)(
)(
)(
)(
;
2
1
2
lg20lg20)(
ωω
ω
ω
ωϕ
ωω
arctgTTarctg
U
V
arctg
T
TkL
−=−==
+−=
Построим ЛАЧХ (рис. 4.12)
3)
Пусть
1
T
ω
<
, тогда пренебрегаем ω и считаем ω
2
≈ 0
k
k
L
lg201lg20lg20)( =−=
ω
4)
Пусть
T
1
>
ω
, тогда
2
1
2
T
>>
ω
)(
2
)(
1
lg20lg20)(
ω
ω
ω
ω
L
L
T
k
L
+
=
−=
Определим наклон L
2
(ω) на декаду
20lg 10 ( 20lg ) 20lg 20lg10 20lg 20 /TTT TдБ дек
ω
ωω ω
−⋅−−⋅=− − + =−
20lgk
40
20
L(ω)
1
-20дБ/дек
Приближенная (асимптотическая)
Погрешность 3 дБ
Точная
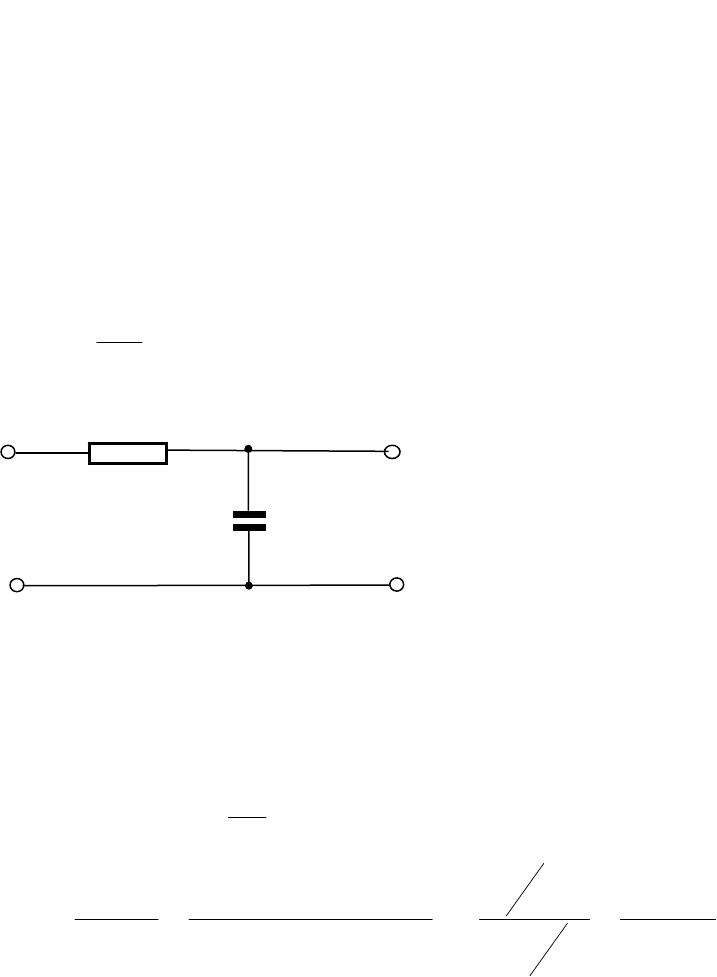
61
Примеры звена.
1. RC–цепь, изображенная на рис. 4.13.
Приведенная RC–цепь описывается уравнением
,uu
d
t
du
RC
12
2
=+
где T=RC – постоянная
времени звена.
Передаточная функция может быть найдена также через комплексные
сопротивления ветвей
1
() () ()
1
22
()
1
() ()[ () ()] 1
121
Up Ipzp
Cp
Wp
Up Ipz p zp RCp
R
Cp
⋅
== == =
+
+
+
.
2. Генератор постоянного тока, приведенный на рис. 4.14.
C
R
u
1
u
2
.
Cp
1
)p(
2
z;R)p(
1
z ==
Ри
Рис. 4.13
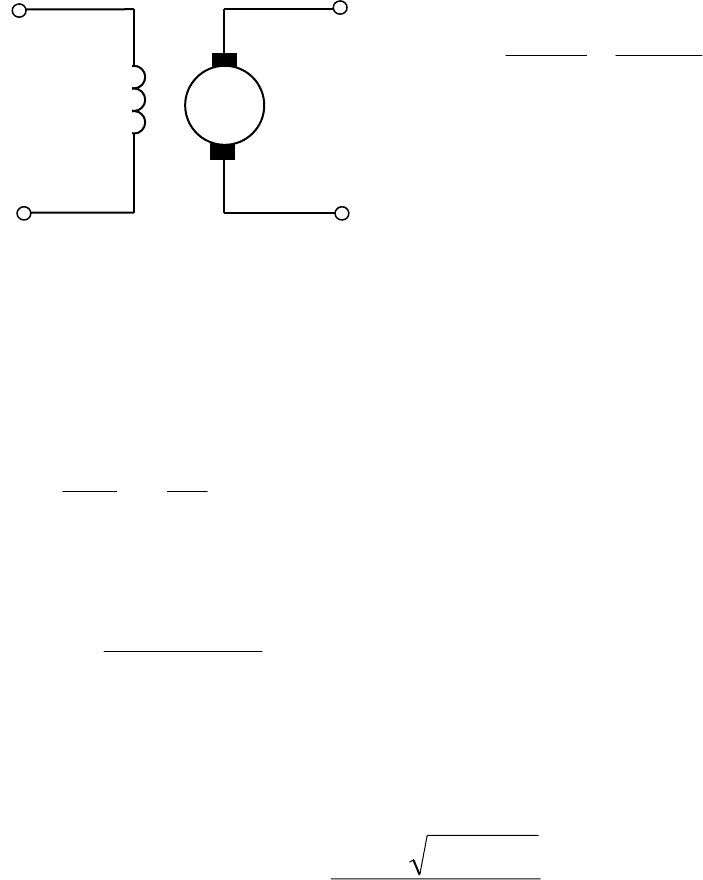
62
Свойства генератора описываются
передаточной функцией
,
1pT
K
)p(U
)p(E
)p(W
В
Г
В
Г
+
==
где U
В
– напряжение обмотки
возбуждения; Е
Г
– э.д.с. генератора; T
В
–
электромагнитная постоянная обмотки
возбуждения; К
Г
– коэффициент
передачи генератора.
4.3. Звено второго порядка
Его динамические свойства описываются дифференциальным
уравнением второго порядка
2
2
22
2121
2
dx dx
TTxkx
dt dt
+
+=.
Звену соответствует передаточная функция:
22
21
()
1
k
Wp
Tp Tp
=
++
.
Характеристическое уравнение звена и его корни имеют вид
;01rTrT
1
22
2
=++
2
2
2
2
2
11
2,1
T2
T4TT
r
−±−
=
.
Возможны два случая:
1. 0T4T
2
2
2
1
<− – корни комплексные, а звено называется колебательным;
2. 0T4T
2
2
2
1
≥− – корни действительные отрицательные, а звено является
апериодическим второго порядка.
4.3.1. Колебательное звено
Передаточную функцию звена в этом случае принято записывать в
следующем виде
U
в
=
x
1
E
г
=
x
2
Г
Рис. 4.14
