Skiadas C.H., Skiadas C. Chaotic Modelling and Simulation. Analysis of Chaotic Models, Attractors and Forms

Подождите немного. Документ загружается.

274 Chaotic Modelling and Simulation

FIGURE 12.8: Box-like orbits

the third power order potential of the H

enon-Heiles model. Box-like orbits, as well

as orbits of other types, arise in this case. Figure 12.8 presents the eﬀect of rota-

tion applied to particles following box-like orbits (left image). The image on the

right represents a four-armed spiral galaxy that results when the moving particles

are rotated by using the rotation equations. As the case under discussion involves

stellar bodies, the rotation angle must be selected to follow an inverse law with re-

gards to the distance r of the particles from the centre of coordinates, as suggested in

chapter 11. In this application, the following equation is used for the rotation angle:

θ = 1 +

+ r)

3/2

The cut-oﬀ radius is equal to r

= 0.1, the simple rotation is expressed by the ﬁrst

term on the right, while the second term represents the inﬂuence of the attracting

forces on the rotating particles.

The Hamiltonian proposed here has the form:

H =

+ v

) + U(x, y)

where the potential U(x, y) is:

U(x , y) =

−

− x

The parameters used in the above simulation were x = 0, y = −0.25, u = 0.23 and

v = 0.07.

The equations for ˙u and ˙v follow from the potential function, and are

−˙u = x + x

− 2xy

−˙v = y − y

− 2x

The maximum U(x, y) is achieved at x = 1/

√

5 and y =

√

5, and it is h =

U(x , y) = 1/5.

Galactic-Type Potentials and the H´enon-Heiles System 275

12.6 The Simplest Form for the Hamiltonian

The simplest form for the Hamiltonian is:

H =

( ˙x

+ ˙y

) +

+ y

) = h

where the potential

U(x , y) =

+ y

)

This gives a family of circles centred at (x, y) = (0, 0) in a (x, y) diagram. The

equations for ¨x and ¨y are:

˙u = ¨x = −x

˙v = ¨y = −y

It is obvious that the minimum acceptable value for the potential is 0 at (x, y) = (0, 0),

while there is no upper limit. The paths are ellipses and, in some cases, circles.

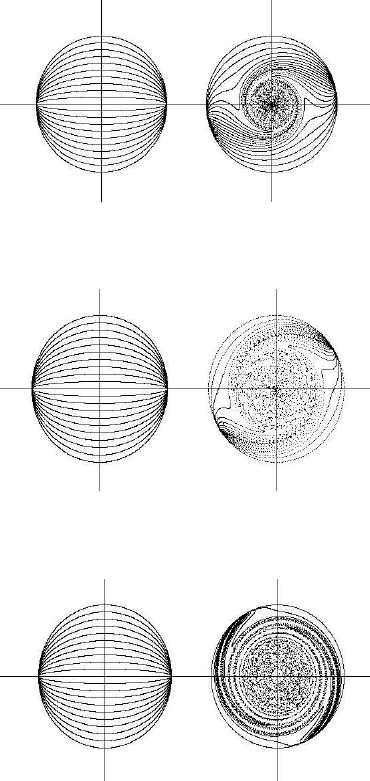
Several paths are drawn in Figure 12.9(a) (left). The starting point is at (x, y) = (1, 0),

u was kept at 0, while the parameter v takes successively the values 0.1, 0.2, . . . , 1.0.

There appear 9 ellipses and one circle for v = 1.0 in the diagram on the left. The

diagram on the right side of the same ﬁgure illustrates the shape the orbits take after

rotation with an angle:

θ =

0.1

(0.001 + r)

The outer circle of the original diagram on the left remains a circle under the

rotation, but the ellipses gradually change shape, resulting in a two-armed spiral.

The two-armed spiral is formed at t = 1, following the original formation of the

circles and ellipses, as illustrated in Figure 12.9(a). If we follow the development

of the curves on the right side of the ﬁgures over time, we observe that there is

an anticlockwise turn of the galaxy-like object, a larger central circle, and more

distinct arms. The cases for t = 5 and t = 20 are presented in Figures 12.9(b) and

Figure 12.9(c).

12.7 Gravitational Attraction

The case of a small mass m attracted by a large mass M has been widely explored.

Here, we assume that the large mass is located at the centre of coordinates, and it

remains stable. A number of particles are attracted by the large mass from their initial

position (x, y), and directed towards the mass. The particles have initial velocities

˙x = u and ˙y = v at position (x, y). In this case, the energy conservation equation

276 Chaotic Modelling and Simulation

(a) t = 1

(b) t = 5

FIGURE 12.9: A simple Hamiltonian: orbits and rotation forms at various

times

Galactic-Type Potentials and the H´enon-Heiles System 277

holds:

E =



+ v



−

GMm

+ v

−

= h

The potential is

U = −

were G is the gravitational constant, and r =

+ y

. By assuming GM = 1, the

equations of motion are:

¨x = ˙u =

¨y = ˙v =

In this computer experiment, we place particles with mass m = 1 at position

(x, y) = (1, 0) and initial velocities u = 0 and v in the interval (0, 1). The v = 1 case

corresponds to a circular path located at (x, y) = (0, 0) and with radius r = 1. The

escape velocity is v =

√

2. In this case, the path is a hyperbola. When v ≥

√

2, the

particles escape to inﬁnity. The ten paths used have velocities v = 0.1, 0.2, . . . , 1.0.

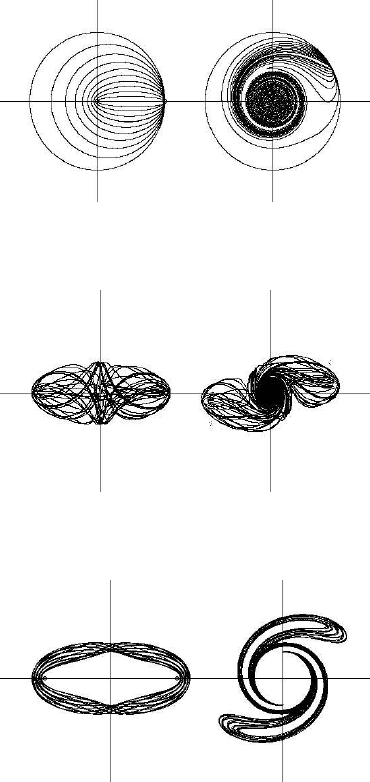
These paths are illustrated in Figure 12.10(a) (left). The right side of Figure 12.10(a)

is the rotation image of the left side after time t = 1. The rotation angle follows the

relation:

θ =

0.5

(0.001 + r)

The resulting shape is that of a one-armed spiral galaxy.

Another computer experiment is based on two attracting masses, located at (x , y) =

(1, 0) and (x, y) = (−1, 0). The Hamiltonian in this case is

H =

+ v

) −

−

= h

where r

(x − 1)

+ y

and r

(x + 1)

+ y

. Excluding the diverging paths,

the resulting image appears in the left part of Figure 12.10(b). In the right part of the

same ﬁgure, the rotation image is illustrated after time t = 1. A two-armed spiral is

formed. The rotation angle is of the form:

θ =

0.1

(0.001 + r)

Another two-armed spiral galaxy is formed after rotation for time t = 1 of the

image resulting when a moving particle is attracted by two masses located at (x, y) =

(1, 0) and (x, y) = (−1, 0), as in the previous case, but now with a slightly diﬀerent

rotation angle:

θ =

0.5

(0.001 + r)

278 Chaotic Modelling and Simulation

(a) A single attracting mass

(b) Two attracting masses

FIGURE 12.10: Orbits and rotation forms at time t = 1

Galactic-Type Potentials and the H´enon-Heiles System 279

The initial parameters were x = 1.2, y = 0, u = 0 and v = 3.95. The paths are

illustrated in the left side of Figure 12.10(c), whereas in the right side the rotation

object after time t = 1 is presented.

12.8 A Logarithmic Potential

A logarithmic form for the potential is used in this section to simulate some inter-

esting cases in galaxy formation. The potential has the form

U =



+ x

+ c



where R is the cut-oﬀ radius and c is a parameter. Figure 12.11(a) shows a box orbit

(left). The parameters are R = 0.1, c = 0.8 and the starting values are x = 0, y = 1,

u = 0.2 and v = 0. The right part of Figure 12.11(a) presents the rotation of the

box-like orbit with a rotation angle:

θ =

0.01

(0.001 + r)

A chaotic orbit is illustrated in Figure 12.11(b). The parameters are R = 0.14,

c = 1.25 and the initial conditions are x = 0, y = 0.792121, u = 0.1 and v = 0. A

loop orbit is also possible by using the above potential. The loop avoids the centre, as

illustrated in the Figure 12.11(c), while the rotation image gives a two-armed spiral.

The parameters are R = 0.14, c = 1.25 and the initial conditions are x = 0, y = 0.2,

u = 0.1 and v = 0.

12.9 Hamiltonians with a Galactic Type Potential: The

Contopoulos System

A Hamiltonian with a “galactic type” potential was ﬁrst introduced by Contopou-

los (1958, 1960) in his pioneering work on galaxies. The potential is based on the

addition of two harmonic oscillators, along with higher order terms, to give the form:

U(x , y) =



+ w



− exy

The resulting Hamiltonian is:

H =



+ v



+ U(x, y) = h

280 Chaotic Modelling and Simulation

(a) Box orbit

(b) Chaotic orbit

FIGURE 12.11: Logarithmic potential: orbits and rotation forms at time t = 1

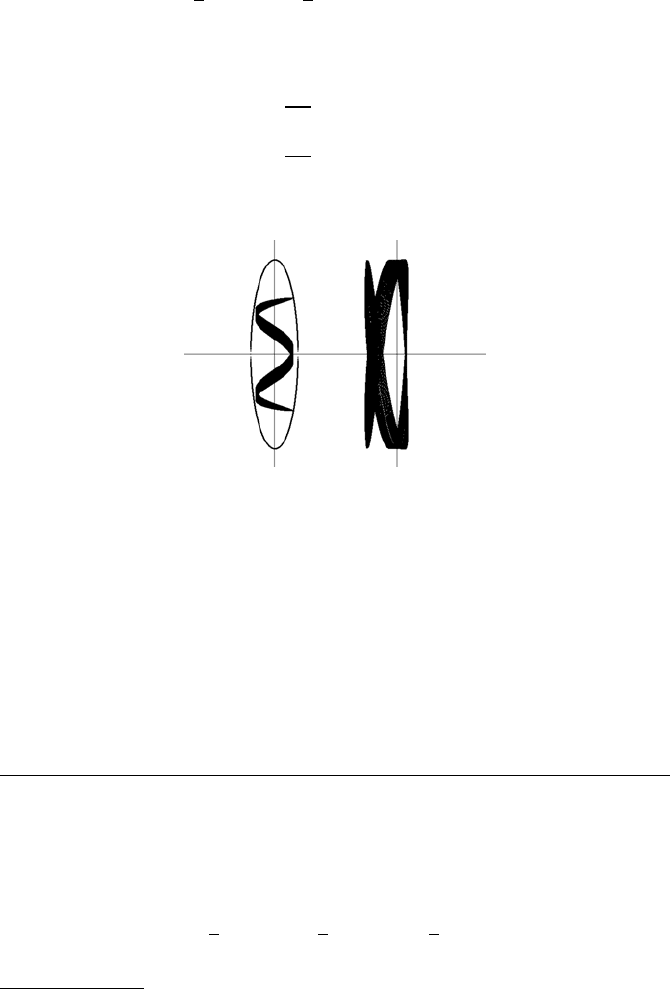
Galactic-Type Potentials and the H´enon-Heiles System 281

Without loss of generality this Hamiltonian can be simpliﬁed to:

H =



+ v





+ y



− exy

= 1/2

where k = w

is the very important resonance ratio. The equations of motion are

given by:

˙u = −

∂U

∂x

= −k

x − ey

˙v = −

∂U

∂y

= y − 2exy

FIGURE 12.12: The Contopoulos system: orbits at resonance ratio 4/1 (left)

and 2/3 (right)

Resonant orbits characterised as 4/1 (left image) and 2/3 (right image) are illus-

trated in Figure 12.12. For the case on the left, the parameters are e = 0.1 and

k = w

= 4/1, and the initial conditions are x = 0.2, y = 0, u = 0 and v = 0.6.

For the case on the right, the parameters are e = 0.1 and k = w

= 2/3, and the

initial conditions are x = 0.1, y = 0, u = 0 and v = 0.9977753.

12.10 Another Simple Hamiltonian System

A very simple Hamiltonian system that shows interesting properties has the fol-

lowing Hamiltonian:

H =



+ v





+ y



−

y = h

Contopoulos (2002).

282 Chaotic Modelling and Simulation

The potential function is:

U(x , y) =



+ y



−

The equations of motion are

˙u = −(x − xy)

˙v = −(y − x

/2)

A number of equipotential curves are drawn based on the equation:



+ y



−

y = h

The analysis of this equation gives the acceptable range 0 < h < 1/2 for h. A

heavy line with equation x =

1 + y represents the h = 1/2 equipotential curve in

Figure 12.13(a). This curve, and the line y = 1, deﬁne the space where the closed

equipotential curves are located.

Particle orbits at high energy level for this Hamiltonian system are illustrated in

Figure 12.13(b). The parameters and initial values are: h = 1/2 − 0.001, x = 0.97,

y = 0, u = 0, and v is estimated from the Hamiltonian function.

(a) Equipotential curves (b) Orbits at high energy level

FIGURE 12.13: Another simple Hamiltonian system

Galactic-Type Potentials and the H´enon-Heiles System 283

Questions and Exercises

1. Consider the set of parametric equations:

x = sin(at)

y = sin(bt )

(a) Draw the curve corresponding to this system when the parameters are

a = 2 and b = 1.

(b) Determine the implicit equation for the curve in the case where a = 2

and b = 1.

(d) Consider the more general system:

x = sin(at + c)

y = sin(bt )

Examine the curves arising for various integer values for a, b, and for

c = π/k, k ∈ N.

2. Consider the system:

n+1

= x

+ a sin(y

)

n+1

= x

− a sin(x

n+1

)

(a) Determine the ﬁxed points of this system, and their stability.

(b) Compare this system to the system (12.5), and draw the characteristic

graphs of this system, especially the (x

, y

) diagrams, for various values

of the parameter a.

3. Draw the (x, y), (u, v), (x, u) and (y, v) diagrams for the discrete system (12.4)

for c = 0.1.

4. Draw the (x, y), (u, v), (x, u) and (y, v) diagrams for the Henon-Heiles sys-

tem (12.3).