Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

The Black-Litterman Approach to Portfolio Optimization

13.1 Overview

Chapters 8–12 have set out the classic approach to portfolio optimization

that was ﬁ rst explicated by Harry Markowitz in the 1950s and subse-

quently expanded by Sharpe (1964), Lintner (1965), and Mossin (1966).

An enormous academic and practitioner literature (as well as several

Nobel prizes in economics) testiﬁ es to the impact of this new point of

view on asset valuation and portfolio choice. Today no conversation

about a stock’s risk is complete without mentioning its beta, and discus-

sions of portfolio performance regularly invoke the alpha (both of these

topics are discussed in Chapter 11).

It is not an exaggeration to say that Markowitz changed the paradigm

of investment management. Well before Markowitz, individual investors

knew that they should “diversify” and not “put all their eggs in one

basket.” But Markowitz and those who followed him gave statistical and

implementational meaning to these clichés. Modern portfolio theory

(MPT) changed the way intelligent investors discuss investment.

Nevertheless, MPT has disappointed. It is possible to come away from

a standard textbook discussion of portfolio optimization with the impres-

sion that a ﬁ xed set of mechanical optimization rules, combined with a

bit of knowledge about personal preferences, sufﬁ ces to deﬁ ne an

investor’s optimal portfolio. Anyone who has tried to implement portfo-

lio optimization using market data knows that the dream is often a

nightmare. Implementations of portfolio theory produce wildly unreal-

istic portfolios with huge short positions and correspondingly imaginary

long positions.

The main problem with the mechanical implementation of portfolio

optimization is that historical asset return data produce bad predictions

for future asset returns. The estimation of the covariances between asset

returns and the estimation of expected returns—the underpinnings of

portfolio theory—from historical data often produces unbelievable

numbers.

1. It might be thought that limiting short sales, as we have illustrated in Chapter 12, could

solve some of these problems. However, short-sale limitations severely restrict the

investible asset universe. In many cases short-sales are caused by bad historical returns

that are not necessarily indicative of future anticipated returns; investors may want to

purchase assets with these properties despite their “bad” histories.

350 Chapter 13

In Chapter 10 we alluded to some of these problems in the context of

estimating the variance-covariance matrix. There we showed that histori-

cal data may not be the best way to estimate this matrix; other methods—

in particular the “shrinkage” methods—may produce more reliable

estimates of the covariances. In this chapter we take things a step further.

We illustrate the problems of standard portfolio optimization by using a

10-asset portfolio problem. The MPT optimization for our data produces

an insane “optimal” portfolio, with many huge long and short positions.

The problems of portfolio optimization illustrated in our example are,

unfortunately, not unusual. Using the data in a mechanical way to derive

“optimal” portfolios simply doesn’t work.

In 1991, Fisher Black and Robert Litterman of Goldman-Sachs

published an approach that deals with many of the problematics of port-

folio optimization. Black and Litterman start with the assumption that

an investor chooses his optimal portfolio from among a given group of

assets. This group of assets—it might be the Standard & Poor’s 500 Index,

the Russell 2000, or a mix of international indexes—deﬁ nes the frame-

work within which the investor chooses his portfolio. The investor’s uni-

verse of assets deﬁ nes a benchmark portfolio.

The Black-Litterman model takes as its starting point the assumption

that, in the absence of additional information, the benchmark cannot be

outperformed. This assumption is based on much research, which shows

that it is very difﬁ cult to outperform a typical well-diversiﬁ ed

benchmark.

In effect the Black-Litterman model turns modern portfolio theory on

its head—instead of inputting data and deriving an optimal portfolio, the

2. A recent paper by DeMiguel, Garlappi, and Uppal (2007), “Optimal versus Naive

Diversiﬁ cation: How Inefﬁ cient Is the 1/N Portfolio Strategy?,” forthcoming in The

Review of Financial Studies, illustrates how badly mechanical optimization works. The

authors examine optimal allocations among ten sector portfolios. They ﬁ nd that a naive

portfolio allocation rule of investing equal proportions in each portfolio—irrespective

of market values—outperforms more sophisticated data-based optimizations.

3. According to Lipper Analytical Services, “over the ten years ended in June 2000, more

than 80% of ‘general equity’ mutual funds, meaning garden variety stock funds, under-

performed the Standard and Poor’s 500 Index—the major benchmark for stock mutual

funds” (quoted in http://www.fool.com/Seminars/OLA/2001/Retire1_4C.htm). Or,

from a well-known academic: “Professional investment managers, both in the U.S. and

abroad, do not outperform their index benchmarks” Burton G. Malkiel, “Reﬂ ections

on the Efﬁ cient Market Hypothesis: 30 Years Later.” The Francial Review, Vol. 40, 2005,

pp. 1–9.)

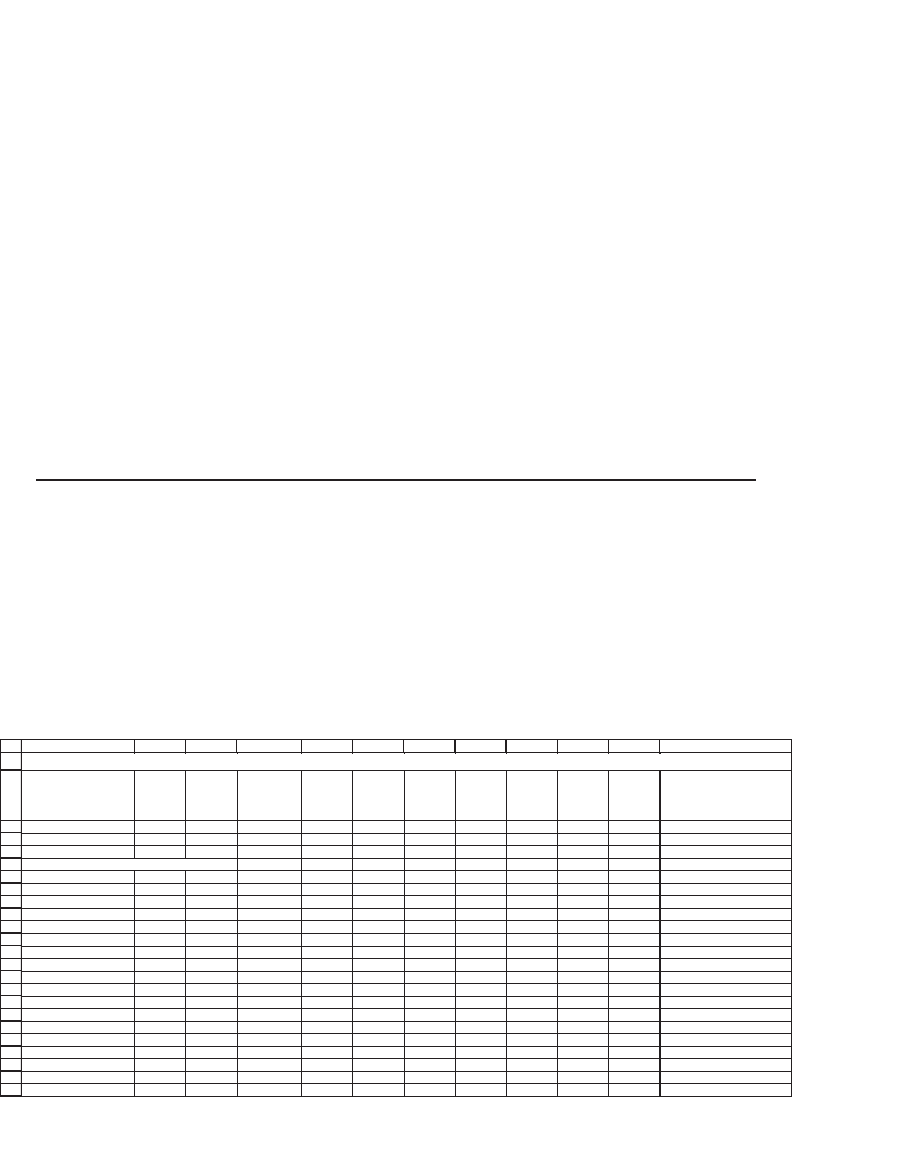
351 The Black-Litterman Approach to Portfolio Optimization

BL approach assumes that a given portfolio is optimal and from this

assumption derives the expected returns of the benchmark components.

The implied vector of expected benchmark returns is the starting point

of the BL model.

The BL implied asset returns can be interpreted as the market’s infor-

mation about the future returns of each asset in the benchmark portfolio.

If our investor agrees with this market assessment, he’s ﬁ nished: He can

then buy the benchmark, knowing that it is optimal. But what if he

disagrees with one or more of the implied returns? Black and Litterman

show how the investor’s opinions can be incorporated into the optimiza-

tion problem to produce a portfolio that is better for the investor.

In this chapter we start with an illustration of the problematics of MPT.

We then go on to illustrate the Black-Litterman approach.

13.2 A Naive Problem

We start with a naive, though representative, problem: The Super Duper

Fund has set its benchmark portfolio to be a portfolio composed of 10

leading stocks. Joanna Roe, a new portfolio analyst for the Super Duper

Fund, has decided to use portfolio theory to recommend optimal port-

folio holdings based on this benchmark. The following screen gives ﬁ ve

years of monthly price data on these stocks as of 1 July 2006 (note that

some of the rows have been hidden):

ABCDEFGHIJK L

General

Motors

Home

Depot

International

Paper

Hewlett-

Packard

HPQ

Altria

American

Express

AXP

Alcoa

Aluminum

DuPont

Merck

MRK

MMM

Equity value 16.85 73.98 15.92 88.37 153.33 65.66 28.16 38.32 79.51 60.9

Benchmark proportion 2.71% 11.91% 2.56% 14.23% 24.69% 10.57% 4.53% 6.17% 12.80% 9.81% <

=K3/SUM($B$3:$K$3)

Monthly price data (includes dividends)

1-Jun-01 50.31 45.26 31.22 26.47 38.74 32.47 36.06 40.88 50.74 51.56

2-Jul-01 49.72 48.26 35.64 22.83 35.61 33.82 35.37 36.29 53.98 50.55

1-Aug-01 43.14 44.06 35.32 21.48 37.10 30.54 34.50 35.01 51.96 47.30

4-Sep-01 33.81 36.79 30.66 14.92 37.79 24.37 28.06 32.07 53.16 44.71

1-Oct-01 32.56 36.66 31.50 15.65 36.63 24.75 29.34 34.18 50.93 47.43

1-Nov-01 39.63 44.78 35.37 20.45 36.92 27.68 35.09 38.21 54.07 52.33

3-Dec-01 38.75 48.97 35.73 19.17 36.34 30.02 32.32 36.63 47.18 53.99

2-Jan-02 40.77 48.09 36.99 20.64 39.71 30.22 32.59 38.06 47.48 50.70

1-Feb-02 42.67 48.00 38.96 18.78 41.73 30.72 34.31 40.68 49.21 54.16

1-Mar-02 48.69 46.71 38.30 16.81 42.21 34.52 34.47 40.95 46.46 52.81

1-Apr-02 51.67 44.56 36.90 16.02 43.62 34.64 31.08 38.65 43.85 57.77

1-Dec-05 19.01 40.17 33.12 28.48 73.08 51.23 29.30 41.77 31.10 76.60

3-Jan-06 23.56 40.24 32.15 31.02 70.75 52.33 31.21 38.48 33.73 71.91

1-Feb-06 20.11 41.83 32.53 32.64 70.32 53.76 29.19 39.91 34.09 73.20

1-Mar-06 21.06 42.13 34.32 32.81 70.06 52.43 30.43 41.87 34.83 75.29

3-Apr-06 22.66 39.77 36.09 32.38 72.34 53.81 33.63 43.74 34.03 84.98

1-May-06 26.93 37.97 33.98 32.29 71.54 54.36 31.72 42.53 33.29 83.66

1-Jun-06 29.79 35.79 32.30 31.68 73.43 53.22 32.36 41.60 36.43 80.77

PRICE AND MARKET CAP DATA FOR 10 COMPANIES

352 Chapter 13

Row 3 gives the current equity value of each of the benchmark stocks,

and row 4 computes the benchmark proportions—the individual equity

values divided by the total market capitalization of the benchmark.

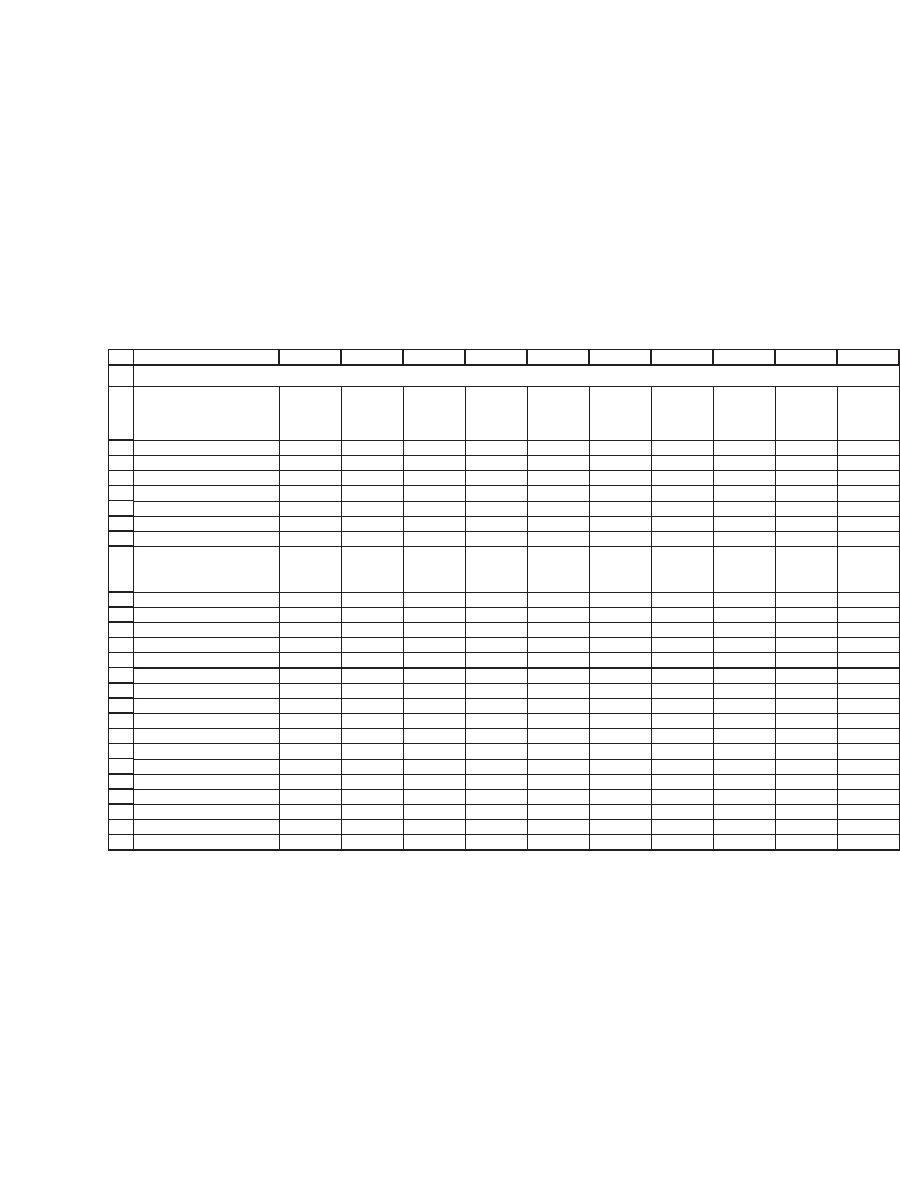
Following the procedures described in Chapters 9 and 10, Joanna ﬁ rst

transforms the price data to returns and then computes a variance-

covariance matrix for these returns:

ABCDEFGHIJ

General

Motors

Home

Depot

Internation

al paper

Hewlett-

Packard

HPQ

Altria

American

Express

AXP

Alcoa

Aluminum

DuPont

Merck

MRK

MMM

Equity value (billion $) 16.85 73.98 15.92 88.37 153.33 65.66 28.16 38.32 79.51 60.9

Benchmark proportion 2.71% 11.91% 2.56% 14.23% 24.69% 10.57% 4.53% 6.17% 12.80% 9.81%

Mean return -0.87% -0.39% 0.06% 0.30% 1.07% 0.82% -0.18% 0.03% -0.55% 0.75%

Return sigma 10.78% 8.41% 6.23% 10.80% 8.71% 6.43% 9.54% 6.12% 8.06% 5.54%

Date GM HD IP HPQ MO AXP AA DD MRK MMM

2-Jul-01 -1.18% 6.42% 13.24% -14.79% -8.42% 4.07% -1.93% -11.91% 6.19% -1.98%

1-Aug-01 -14.20% -9.11% -0.90% -6.10% 4.10% -10.20% -2.49% -3.59% -3.81% -6.65%

4-Sep-01 -24.37% -18.03% -14.15% -36.44% 1.84% -22.57% -20.66% -8.77% 2.28% -5.63%

1-Oct-01 -3.77% -0.35% 2.70% 4.78% -3.12% 1.55% 4.46% 6.37% -4.29% 5.91%

1-Nov-01 19.65% 20.01% 11.59% 26.75% 0.79% 11.19% 17.90% 11.15% 5.98% 9.83%

3-Dec-01 -2.25% 8.94% 1.01% -6.46% -1.58% 8.12% -8.22% -4.22% -13.63% 3.12%

2-Jan-02 5.08% -1.81% 3.47% 7.39% 8.87% 0.66% 0.83% 3.83% 0.63% -6.29%

1-Sep-05 -11.06% -5.56% -3.48% 5.32% 5.28% 3.90% -9.25% -1.02% -3.66% 3.05%

3-Oct-05 -11.10% 7.33% -2.08% -4.05% 1.81% -0.78% -0.54% 6.25% 3.63% 3.50%

1-Nov-05 -20.55% 2.02% 8.56% 5.66% -3.06% 3.28% 12.70% 3.39% 5.40% 3.77%

1-Dec-05 -12.03% -3.16% 6.39% -3.32% 3.67% 0.08% 7.58% -0.60% 7.86% -1.26%

3-Jan-06 21.46% 0.17% -2.97% 8.54% -3.24% 2.12% 6.32% -8.20% 8.12% -6.32%

1-Feb-06 -15.83% 3.88% 1.18% 5.09% -0.61% 2.70% -6.69% 3.65% 1.06% 1.78%

1-Mar-06 4.62% 0.71% 5.36% 0.52% -0.37% -2.51% 4.16% 4.79% 2.15% 2.82%

3-Apr-06 7.32% -5.76% 5.03% -1.32% 3.20% 2.60% 10.00% 4.37% -2.32% 12.11%

1-May-06 17.26% -4.63% -6.02% -0.28% -1.11% 1.02% -5.85% -2.81% -2.20% -1.57%

1-Jun-06 10.09% -5.91% -5.07% -1.91% 2.61% -2.12% 2.00% -2.21% 9.01% -3.52%

RETURN DATA FOR THE SUPER DUPER BENCHMARK PORTFOLIO

13.2.1 Naive Optimization

Using the return data, Joanna computes the sample variance-covariance

matrix of excess returns as illustrated in Chapter 10. To implement the

portfolio optimization, she needs data on the T-bill rate: The 1 July 2006

T-bill rate is 4.83 percent annually, and 4.83 percent/12 = 0.40 percent

monthly. Using the variance-covariance matrix, the T-bill rate, and the

historical mean returns, she computes an “optimal” portfolio by solving

the equation

353 The Black-Litterman Approach to Portfolio Optimization

Optimal portfolio { , , , }

MMM

xx x

12 10

... =

−

⎡

⎣

−



⎢⎢

⎢

⎤

⎦

⎥

∗∗

−

⎡

⎣

⎢

⎤

⎦

⎥

−

[...]11 1

,, ,

MMM



⎥⎥

−

⎡

⎣

⎢

⎤

⎦

⎥

∗

−

MMM

Sum



rrr

fMMM

−

⎡

⎣

⎢

⎤

⎦

⎥

⎡

⎣

⎢

⎤

⎦

⎥

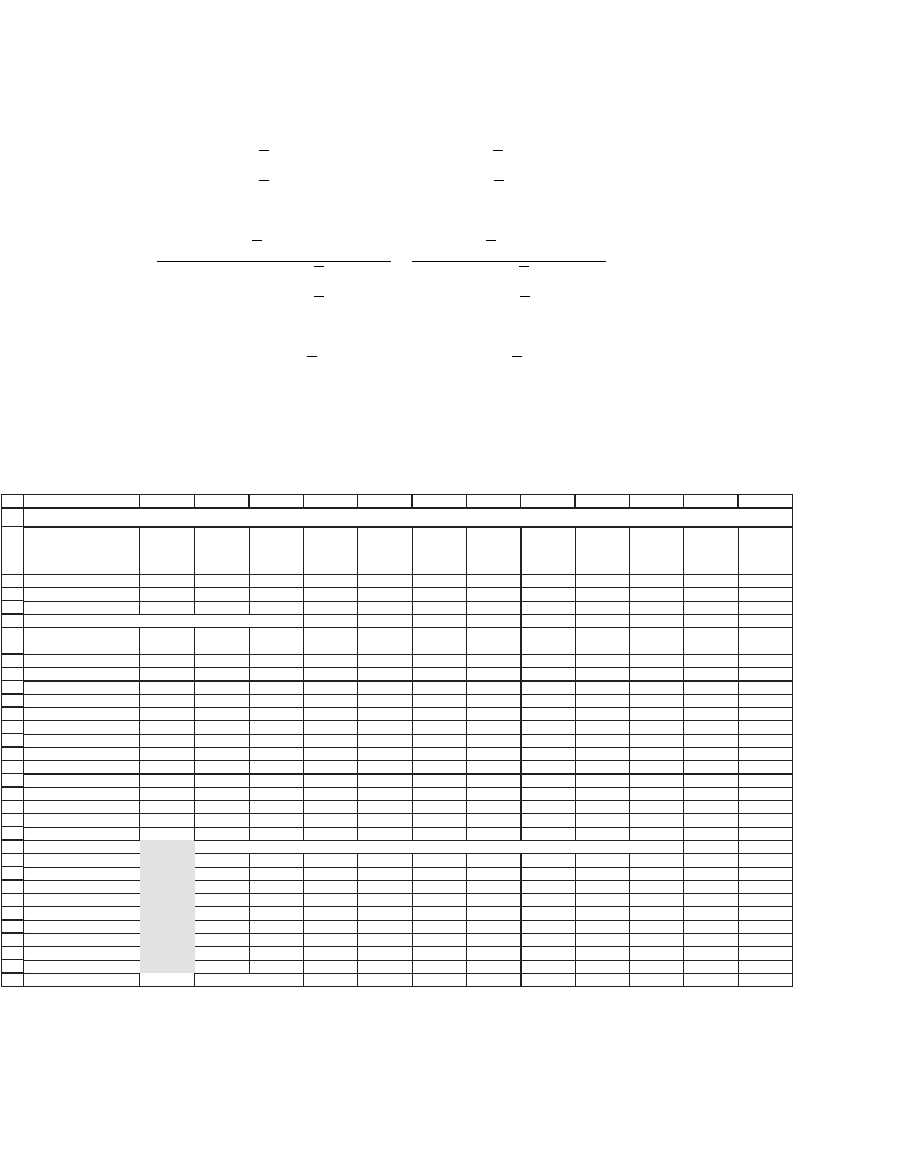
This portfolio is as follows (highlighted):

ABCDEFGHIJKLM

General

Motors

Home

Depot

Internation

al paper

Hewlett-

Packard

HPQ

Altria

American

Express

AXP

Alcoa

Aluminum

DuPont

Merck

MRK

MMM

Equity value 16.85 73.98 15.92 88.37 153.33 65.66 28.16 38.32 79.51 60.9

Benchmark proportion 2.71% 11.91% 2.56% 14.23% 24.69% 10.57% 4.53% 6.17% 12.80% 9.81%

Variance-covariance matrix of excess returns

GM HD IP HPQ MO AXP AA DD MRK MMM

Mean

return

GM 0.0116 0.0030 0.0023 0.0041 0.0013 0.0032 0.0046 0.0018 0.0010 0.0014 -0.87%

HD 0.0030 0.0071 0.0018 0.0042 0.0022 0.0033 0.0045 0.0020 0.0002 0.0018 -0.39%

IP 0.0023 0.0018 0.0039 0.0031 0.0001 0.0023 0.0043 0.0021 0.0012 0.0016 0.06%

HPQ 0.0041 0.0042 0.0031 0.0117 0.0025 0.0048 0.0060 0.0033 0.0019 0.0022 0.30%

MO 0.0013 0.0022 0.0001 0.0025 0.0076 0.0016 0.0018 0.0009 0.0007 0.0008 1.07%

AXP 0.0032 0.0033 0.0023 0.0048 0.0016 0.0041 0.0037 0.0019 0.0011 0.0014 0.82%

AA 0.0046 0.0045 0.0043 0.0060 0.0018 0.0037 0.0091 0.0040 0.0018 0.0024 -0.18%

DD 0.0018 0.0020 0.0021 0.0033 0.0009 0.0019 0.0040 0.0038 0.0016 0.0019 0.03%

MRK 0.0010 0.0002 0.0012 0.0019 0.0007 0.0011 0.0018 0.0016 0.0065 0.0005 -0.55%

MMM 0.0014 0.0018 0.0016 0.0022 0.0008 0.0014 0.0024 0.0019 0.0005 0.0031 0.75%

Current t-bill rate 0.40%

"Optimal" portfolio

GM 480.2% <

{=MMULT(MINVERSE(B8:K17),M8:M17-B19)/SUM(MMULT(MINVERSE(B8:K17),M8:M17-B19))}

HD 981.8%

IP 689.3%

HPQ 221.3%

MO -263.7%

AXP -1763.7%

AA -324.5%

DD 528.8%

MRK 469.5%

MMM -918.9%

Sum of proportions 1 <

=SUM(B22:B31)

SUPER DUPER BENCHMARK PORTFOLIO--NAIVE OPTIMIZATION

354 Chapter 13

The “optimal” portfolio shown in cells B22 : B31 is clearly not practi-

cally implementable: It contains too many large positions (both negative

and positive). Note, for example, the −1763.7 percent short position in

AXP and the 528.8 percent position in DD. Most mutual funds are

prevented from taking short positions, and even funds that sell short will

ﬁ nd it difﬁ cult to short-sell 17.63 times the fund value in AXP or 9.19

times the fund value in MMM. The enormous long positions that result

from these short-sale positions (for example 9.82 times fund value

invested long in HD) are similarly impracticable.

13.2.2 Why Does Naive Optimization Fail?

In some sense the strange portfolio “optimization” positions were

predictable. The spreadsheet that follows highlights some disturbing

features of the data that can partially explain the odd “optimized”

portfolio.

•

A number of the historical mean returns are negative. If we ignore the

effects of correlations, a negative expected return should imply a short

position in the stock. There is, however, a deeper philosophical question

about using past returns as proxies for future expected returns: Even

though the past returns are negative, there is no reason to assume that

the future, expected returns from a stock should be negative. This is one

of the problems when we use historical data to extract anticipations

about the future.

•

The correlations between asset returns are in some cases very large.

Large correlations for a particular stock can lead us to prefer other

stocks with smaller returns but more moderate correlations.

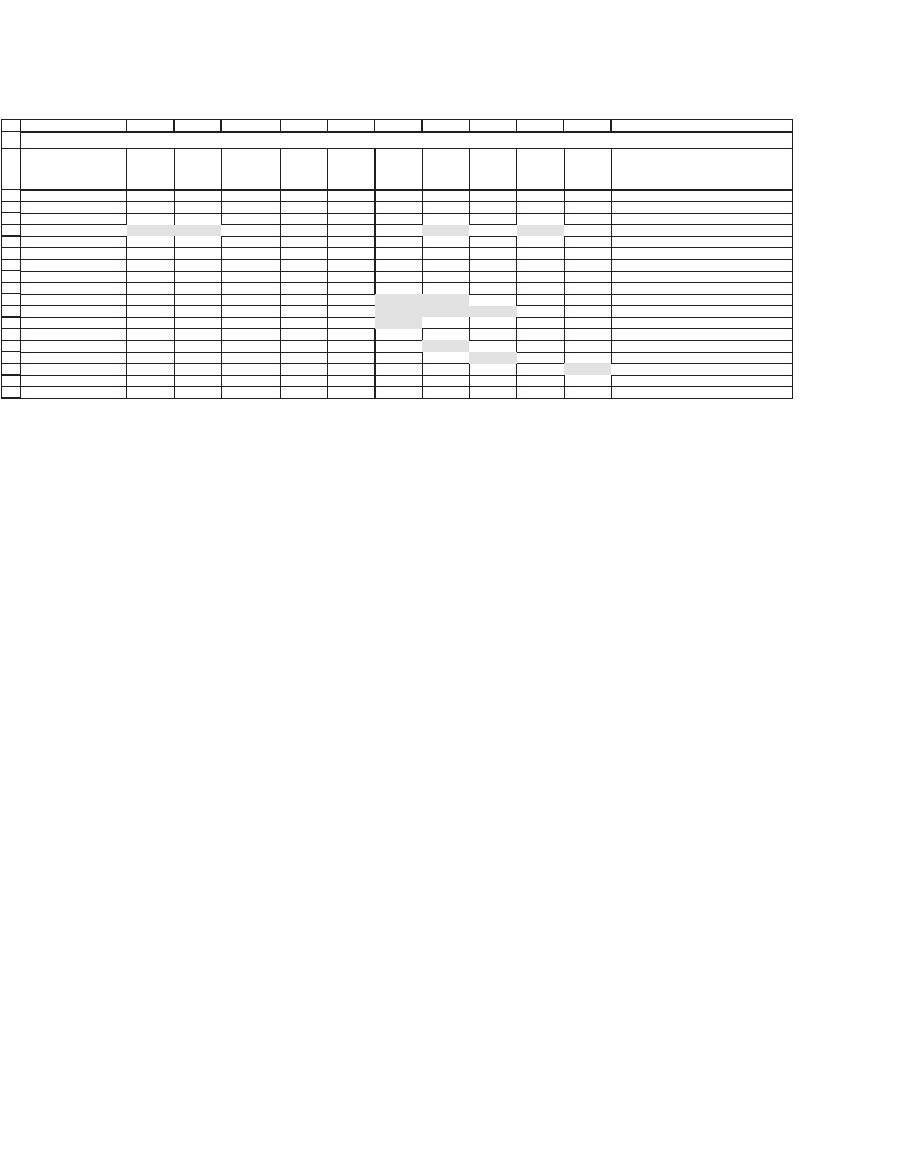
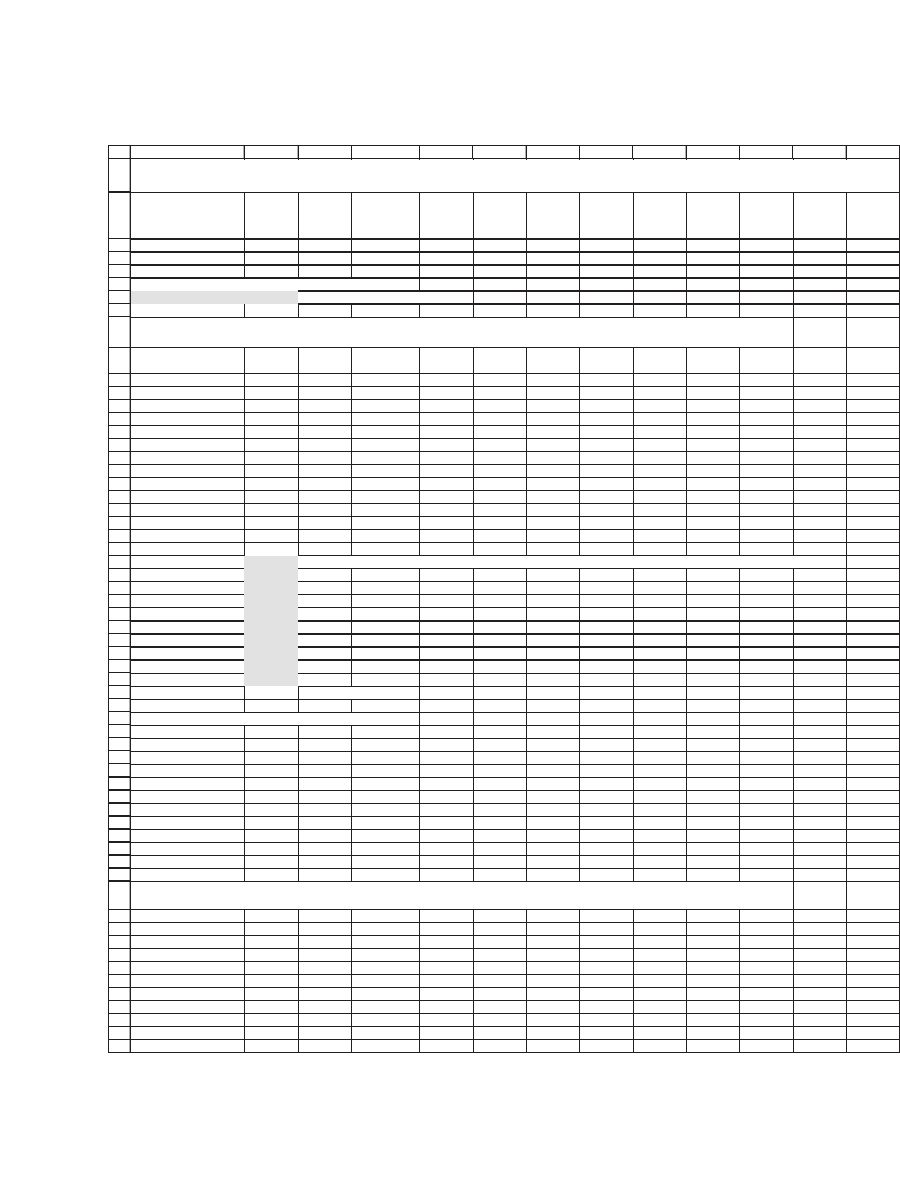
The following spreadsheet highlights stocks with negative historical

returns and stocks whose correlations are greater than 0.5:

355 The Black-Litterman Approach to Portfolio Optimization

13.2.3 What about Changing the Variance-Covariance Matrix?

In Chapter 10 we discussed various methods for shrinking the variance-

covariance matrix. “Shrinkage,” you will recall, is a bit of jargon for

taking a convex combination of the sample var-cov matrix with a diago-

nal matrix of only the variances. Shrinkage methods have been shown to

be effective at improving the performance of the global minimum vari-

ance portfolio (GMVP).

Will shrinkage help us solve the extreme positions of the naive port-

folio optimization? We make this attempt in the next spreadsheet, where

cells B11 : K20 contain a weighted combination of the sample covariance

matrix (B39 : K48) and an all-diagonal matrix of only the variances

(B52 : K61). The weight λ put on the sample covariance matrix is given

in cell B7.

For λ = 0.3, the “optimal” portfolio indeed contains fewer extreme long

and short positions. But it is clear that shrinkage can never solve the

fundamental problem of the data—using negative historical returns as

proxies for expected returns will always produce some negative portfolio

positions in an optimizer. It is this problem which Black and Litterman

solve and which we discuss in the next section.

LKJIHGFEDCBA

General

Motors

Home

Depot

International

Paper

Hewlett-

Packard

HPQ

Altria

American

Express

AXP

Alcoa

Aluminum

DuPont

Merck

MRK

MMM

Equity value 16.85 73.98 15.92 88.37 153.33 65.66 28.16 38.32 79.51 60.9

Benchmark proportion 2.71% 11.91% 2.56% 14.23% 24.69% 10.57% 4.53% 6.17% 12.80% 9.81%

Mean return -0.87% -0.39% 0.06% 0.30% 1.07% 0.82% -0.18% 0.03% -0.55% 0.75%

Return sigma 10.78% 8.41% 6.23% 10.80% 8.71% 6.43% 9.54% 6.12% 8.06% 5.54%

GM HD IP HPQ MO AXP AA DD MRK MMM

GM 1.0000 0.3320 0.3459 0.3534 0.1428 0.4676 0.4430 0.2737 0.1109 0.2277 <

=CORREL($B$24:$B$83,K24:K83)

HD 1.0000 0.3512 0.4618 0.3012 0.6061 0.5618 0.3891 0.0260 0.3800 <

=CORREL($C$24:$C$83,K24:K83)

IP 1.0000 0.4580 0.0159 0.5772 0.7181 0.5400 0.2362 0.4575 <

=CORREL($D$24:$D$83,K24:K83)

HPQ 1.0000 0.2682 0.6965 0.5770 0.4924 0.2232 0.3666

MO 1.0000 0.2839 0.2145 0.1647 0.0955 0.1645

AXP 1.0000 0.6034 0.4855 0.2038 0.3798

AA 1.0000 0.6863 0.2294 0.4525

DD 1.0000 0.3287 0.5606

MRK 1.0000 0.1079

MMM 1.0000

NEGATIVE RETURNS AND HIGH CORRELATIONS

356 Chapter 13

ABCDEFGHIJKL

General

Motors

Home

Depot

International

paper

Hewlett-

Packard

HPQ

Altria

American

Express

AXP

Alcoa

Aluminum

DuPont

Merck

MRK

MMM

Equity value 16.85 73.98 15.92 88.37 153.33 65.66 28.16 38.32 79.51 60.9

Benchmark proportion 2.71% 11.91% 2.56% 14.23% 24.69% 10.57% 4.53% 6.17% 12.80% 9.81%

Variance-covariance matrix of excess returns

Shrinkage factor,

0.3 <

Weight on sample var-cov matrix

GM HD IP HPQ MO AXP AA DD MRK MMM

Mean

return

GM 0.0116 0.0009 0.0007 0.0012 0.0004 0.0010 0.0014 0.0005 0.0003 0.0004 -0.87%

HD 0.0009 0.0071 0.0006 0.0013 0.0007 0.0010 0.0014 0.0006 0.0001 0.0005 -0.39%

IP 0.0007 0.0006 0.0039 0.0009 0.0000 0.0007 0.0013 0.0006 0.0004 0.0005 0.06%

HPQ 0.0012 0.0013 0.0009 0.0117 0.0008 0.0015 0.0018 0.0010 0.0006 0.0007 0.30%

MO 0.0004 0.0007 0.0000 0.0008 0.0076 0.0005 0.0005 0.0003 0.0002 0.0002 1.07%

AXP 0.0010 0.0010 0.0007 0.0015 0.0005 0.0041 0.0011 0.0006 0.0003 0.0004 0.82%

AA 0.0014 0.0014 0.0013 0.0018 0.0005 0.0011 0.0091 0.0012 0.0005 0.0007 -0.18%

DD 0.0005 0.0006 0.0006 0.0010 0.0003 0.0006 0.0012 0.0038 0.0005 0.0006 0.03%

MRK 0.0003 0.0001 0.0004 0.0006 0.0002 0.0003 0.0005 0.0005 0.0065 0.0001 -0.55%

MMM 0.0004 0.0005 0.0005 0.0007 0.0002 0.0004 0.0007 0.0006 0.0001 0.0031 0.75%

Current T-bill rate 0.40%

"Optimal" portfolio

GM 84.3% <

{=MMULT(MINVERSE(B11:K20),M11:M20-B22)/SUM(MMULT(MINVERSE(B11:K20),M11:M20-B22))}

HD 96.4%

IP 50.2%

HPQ -3.6%

MO -76.1%

AXP -134.6%

AA 32.5%

DD 62.5%

MRK 112.1%

MMM -123.8%

Sum of proportions 1 <

=SUM(B25:B34)

Variance-covariance matrix of excess returns

GM HD IP HPQ MO AXP AA DD MRK MMM

GM 0.0116 0.0030 0.0023 0.0041 0.0013 0.0032 0.0046 0.0018 0.0010 0.0014

HD 0.0030 0.0071 0.0018 0.0042 0.0022 0.0033 0.0045 0.0020 0.0002 0.0018

IP 0.0023 0.0018 0.0039 0.0031 0.0001 0.0023 0.0043 0.0021 0.0012 0.0016

HPQ 0.0041 0.0042 0.0031 0.0117 0.0025 0.0048 0.0060 0.0033 0.0019 0.0022

MO 0.0013 0.0022 0.0001 0.0025 0.0076 0.0016 0.0018 0.0009 0.0007 0.0008

AXP 0.0032 0.0033 0.0023 0.0048 0.0016 0.0041 0.0037 0.0019 0.0011 0.0014

AA 0.0046 0.0045 0.0043 0.0060 0.0018 0.0037 0.0091 0.0040 0.0018 0.0024

DD 0.0018 0.0020 0.0021 0.0033 0.0009 0.0019 0.0040 0.0038 0.0016 0.0019

MRK 0.0010 0.0002 0.0012 0.0019 0.0007 0.0011 0.0018 0.0016 0.0065 0.0005

MMM 0.0014 0.0018 0.0016 0.0022 0.0008 0.0014 0.0024 0.0019 0.0005 0.0031

GM HD IP HPQ MO AXP AA DD MRK MMM

GM 0.0116 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

HD 0.0000 0.0071 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

IP 0.0000 0.0000 0.0039 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

HPQ 0.0000 0.0000 0.0000 0.0117 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

MO 0.0000 0.0000 0.0000 0.0000 0.0076 0.0000 0.0000 0.0000 0.0000 0.0000

AXP 0.0000 0.0000 0.0000 0.0000 0.0000 0.0041 0.0000 0.0000 0.0000 0.0000

AA 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0091 0.0000 0.0000 0.0000

DD 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0038 0.0000 0.0000

MRK 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0065 0.0000

MMM 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0031

SUPER DUPER BENCHMARK PORTFOLIO--NAIVE OPTIMIZATION WITH

SHRUNK VARIANCE-COVARIANCE MATRIX

Pure diagonal matrix. The array formula in the cells produces a matrix with only variances on the diagonal and zero

elsewhere. {=IF(B51:K51=A52:A61,B39:K48,0)}

The following matrix is a weighted combination of the sample variance-covariance matrix and a pure diagonal matrix of only variances.

{=B7*B39:K48+(1-B7)*B52:K61}

357 The Black-Litterman Approach to Portfolio Optimization

13.3 Black and Litterman’s Solution to the Optimization Problem

The Black-Litterman approach provides an initial solution to the

optimization problem we have presented. The BL approach is composed

of two parts:

Step 1: What does the market think? A vast amount of ﬁ nancial research

shows that it is difﬁ cult to beat the returns of benchmark portfolios. The

ﬁ rst step of the BL approach takes this research as a starting point. It

assumes that the benchmark is optimal and derives the expected returns

of each asset under this assumption. To put it another way, in Step 1 we

compute the expected returns of the assets that would make the investor

choose the benchmark using the optimization techniques in Chapters

9–11.

Step 2: Incorporating investor opinions. In Step 1, Black and Litterman

show how to compute the benchmark asset returns based on the assump-

tion of optimality. Suppose the investor has divergent opinions from

these market-based expected returns. Step 2 shows how to incorporate

these opinions into the optimization procedure. Note that—because of

the correlations between asset returns—an investor’s opinion about any

particular asset’s returns will affect all the other expected returns. A

critical part in Step 2 is to adjust all asset returns for an investor’s opinion

about any return.

An investor who follows the Black-Litterman procedure starts off by

seeing what the market weights imply for the expected returns. He can then

adjust these weights by adding his own opinions about any asset’s expected

returns. In the next two sections we discuss these two steps in detail.

13.4 Black-Litterman Step 1: What Does the Market Think?

As shown in Chapter 9, an optimal portfolio must solve the equation

Efficient

portfolio

proportions

Variance-

covarianc

⎡

⎣

⎢

⎤

⎦

⎥

= ee

matrix

Expected

portfolio

returns

⎡

⎣

⎢

⎤

⎦

⎥

∗

⎡

⎣

⎢

⎤

⎦

⎥

−

−1

ssk-free rate

Normalize to sum to 1

⎧

⎨

⎪

⎩

⎪

⎫

⎬

⎪

⎭

⎪

↑

 