Сидельников В.М. Теория кодирования. Справочник по принципам и методам кодирования
Подождите немного. Документ загружается.


s + (N − s)H
³
N−s−λ
√
N
2(N−s)
´
s
[2
−r
N, (1 − 2
−r
)N] s
N
³
2
−r
+ (1 − 2
−r
)H
³
1
2
−
λ
2(1−2
−r
)
√
N)
´´
s = 2
−r
N
H
µ
1
2
(1 − x)
¶
= 1 − ln
−1
2
∞
X
j=1
x
2j
2j(2j − 1)
< 1 −
x
2
2 ln 2
,
2
−r
+ (1 − 2
−r
)H
µ
1
2
−
λ
2(1 − 2
−r
)
√
N)
¶
− H
µ
1
2
−
λ
2
√
N
¶
< −
λ
2
2N(2
r
− 1) ln 2
H(t, s)
¡
N
t
¢
≤ C
7
exp
2
½
ε(r)λ
2
2 ln 2
¾
¤
m → ∞, r = const A
RM
r,m
RM
r,m
e t =
wt(e) <
1
2
(N −C
r
m
r
2
√
N) C
r
r
F
m
2
F
2
m
F
m
2
F
m
2
F
2
m
F
m
2
F
2
m
F
2
F
2
m
2
p > 2
T r(x) = x+x
2
+···+x
2
m−1
, x ∈ F
2
m
,
T r(f(x))
f(x) =
P
t
i=0
α
i
x
i
F
2
m
x m−
x F
2
m

F
2
T r(x) ∈ F
2
T r
2
(x) = T r(x).
Ω = {ω
1
, . . . , ω
m
} F
p
m
F
p
x ∈ F
2
m
x = x
1
ω
1
+ ··· + x
m
ω
m
, x
j
∈ F
p
.
T r(f(x)), f(x) =
P
t
i=0
α
i
x
i
∈ F
2
m
[x],
x
1
, . . . , x
m
∈ F
p
F
p
F
p
T r(f(x)) =
t
X
i=0
T r(α
i
(x
1
ω
1
+ ··· + x
m
ω
m
)
i
) =
=
t
X
i=0
X
1≤j
1
,...,j
i
≤m
x
j
1
···x
j
i
T r(α
i
ω
j
1
···ω
j
i
).
C
h
j j
0
C
h
= {hp
s
mod (p
m
−1)|s = 0, . . . , m−1} j
0
= jp
u
≡ hp
s
mod (p
m
−1)
u, s, 0 ≤ u, s < m
0 ≤ j ≤ p
m
− 1 j = j
0
+ j
1
p + ··· + j
m−1
p
m−1
, j
i
= {0, . . . , p − 1}
j p j = {j
0
, j
1
, . . . , j
m−1
}
jp = {j
m−1
, j
0
, . . . , j
m−2
} j
wc(j) j wc(j) = j
0
+ ··· + j
m−1
wc(j) = w c (j
0
)
j j
0
C
h
T r(α(x
1
ω
1
+···+ x
m
ω
m
)
j
)
x
1
, . . . , x
m
F
p
wc(j)
T r(α(x
1
ω
1
+ ··· + x
m
ω
m
)
j
) = T r(α
m−1
Y
u=0
(x
1
ω
p
u
1
+ ··· + x
m
ω
p
u
m
)
j
u
).
(x
1
ω
p
u
1
+ ··· + x
m
ω
p
u
m
)
j
u
j
u
T r(α(x
1
ω
1
+ ··· + x
m
ω
m
)
j
) wc(j)
¤
T r(f(x)), f(x) ∈ F
p
m
[x]
T r(f(x)) T r(f (x)) = (T r(f (α
1
)), . . . , T r(f(α
p
m
))), {α
1
, . . . , α
p
m
} = F
p
m
p = 2 LT
r
T r(αx
j
) = T r(α(x
1
ω
1
+ ··· + x
m
ω
m
)
j
), α ∈ F
2
m
wc(j) ≤ r
LT
r
= RM
r

LT
m
⊆ RM
r
dimLT
m
≥ dimRM
r
C
r
j wc(j) ≤ r C
r
j
wt(j)
r |C
r
| = 1 +
¡
m
1
¢
+ ··· +
¡
m
r
¢
C
r
C
h
C
r
=
[
wc(h)≤r
C
h
,
C
h
h r
{T r(αx
j
)|α ∈
F
2
m
} |C
h
| C
h
j
{T r(α
j
x
j
)|j ∈
J} J
C
h
{T r(x
j
)|j ∈
C
r
; α ∈ F
2
m
}
X
wc(h)≤r
|C
h
| = |C
r
| = 1 +
µ
m
1
¶
+ ··· +
µ
m
r
¶
,
P
wc(h)≤r
C
h
h r
¤
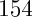

T r(x) = x + x
2
+ ··· + x
2
m−1
b 6= 0
X
x∈F
2
m
(−1)
T r(bx)
= 0.
Q(a, b) =
X
x∈F
2
m
(−1)
T r(ax
3
+bx)
m = 2t − 1 a 6= 0
|Q(a, b)| =
(
0, T r(b) = 1 ,
2
m+1
2
, T r(b) = 0
.
m = 2t a 6= 0
|Q(a, b)| =
2
m
2
, 1 + az
3
= 0,
F
2
m
,
2
m+2
2
, 1 + az
3
= 0,
F
2
m
T r
4
(ba
−
1
3
) = 0,
0, 1 + az
3
= 0,
F
2
m
T r
4
(ba
−
1
3
) 6= 0
,
T r
4
(x) =
P
t
s=0
x
2
2s
F
4
F
2
m
F
4
a = 0 b 6= 0
Q(a, b) = 0.

Q
2
(a, b) =
X
x,y∈F
2
m
(−1)
T r(ax
3
+bx+ay
3
+by)
=
X
z,y∈F
2
m
(−1)
T r(a(y+z)
3
+b(y+z)+ay
3
+by)
=
=
X
z,y∈F
2
m
(−1)
T r(a(zy
2
+z
2
y+az
3
)+bz)
=
X
z,y∈F
2
m
(−1)
T r(ay
2
(z+az
4
)+az
3
+bz)
.
T r(z) = T r(z
2
)
a 6= 0
=
X
y∈F
2
m
(−1)
T r(ay
2
(az
4
+z))
=
(
0, az
4
+ z 6= 0 ,
2
m
, az
4
+ z = 0
.
Q
2
(a, b) = 2
m
g
X
(−1)
T r(1+bz)
,
f
P
az
4
+ z = 0
F
2
m
z + az
4
= 0, a 6= 0, z
0
= 0
1 + az
3
= 0
m z
0
=
a
−
1
3
3 2
m
−1 F
2
m
Q
2
(a, b) = 2
m
µ
1 + (−1)
T r
1+ba
−
1
3
¶
= 2
m
µ
1 − (−1)
T r
ba
−
1
3
¶
,
T r(1) = 1
m 1 + az
3
= 0, a 6= 0,
F
2
m
z
0
, ξz
0
, ξ
2
z
0
ξ
1 F
4
⊆ F
2
m
c ∈ F
2
m
X
ξ∈F
4
(−1)
T r(ξc)
=
(
0, T
4
(c) 6= 0 ,
4, T r
4
(c) = 0
,
¤
N(a, b)
T r(ax
3
+ bx) = 0, x ∈ F
2
l
N(a, b) =
1
2
(2
m
− Q(a, b)), m > 2,

s(ax) =
t
X
i=0
(ax)
2
i
+1
, a ∈ F
2
m
T (a, b) =
X
x∈F
2
m
(−1)
T r(s(ax)+bx)
.
s(az + ay) = s(az) + s(ay) +
t
X
i=0
((az)
2
i
ay + (ay)
2
i
az), a, b ∈ F
2
m
.
m = 2t − 1 a 6= 0
|T (a, b)| = 2
m
³
1 + (−1)
T r(
b
a
)
´
=
(
0, T r(
b
a
) = 1 ,
2
m+1
2
, T r(
b
a
) = 0
.
T
2
(a, b) =
X
x,y∈F
2
m
(−1)
T r(s(ax)+bx)+s(ay)+by)
=
X
z,y∈F
2
m
(−1)
T r(s(az+ay)+s(ay)+bz)
=
=
X
z,y∈F
2
m
(−1)
T r(s(az)+
P
t
i=0
((az)
2
i
ay+(ay)
2
i
az)+bz)
=
X
z,y∈F
2
m
(−1)
T r(s(az)+ay
P
t
i=0
((az)
2
i
+(az)
2
−i
)+bz)
=
= 2
m
g
X
(−1)
T r(s(az)+bz)
,
f
P
t
X
i=0
((az)
2
i
+ (az)
2
−i
) = 0,
F
2
m
(az)
2
−i
= (az)
2
m−i
P
t
i=0
((az)
2
i
+(az)
2
−i
) =
P
m−1
i=1
(az)
2
i
= f(x)
f(x) x ∈ F
m
(T r
m−1
(ax))
2
T r
m−1
(y)
F
2
m−1
T r
m−1
(y) 2
m−2
F
2
m−1
(T r
m−1
(y
)
)
2
F
2
m
F
2
= F
2
m
T
F
2
m−1
F
2
m
0 a
−1
¤
T (a, a
0
, b) =
X
x∈F
2
m
(−1)
T r(s(ax)+s(a
0
x)+bx)
.

m = 2t − 1 a, a
0
6= 0, a 6= a
0
|T (a, a
0
, b)|
2
=
¯
¯
¯
¯
¯
X
x∈F
2
m
(−1)
T r(s(ax)+s(a
0
x)+bx)
¯
¯
¯
¯
¯
2
=
=
2
m
µ
1 + (−1)
T r
s(
a
2
a
2
+a
0
2
)+s(
aa
0
a
2
+a
0
2
)+
ab
a
2
+a
0
2
¶
, T r(
a
a+a
0
) = 1 ,
2
m
Ã
1 + (−1)
T r
s(
a
0
2
a
2
+a
0
2
)+s(
aa
0
a
2
+a
0
2
)+
a
0
b
a
2
+a
0
2
!
, T r(
a
0
a+a
0
) = 1
.
T r(
a
a+a
0
) + T r(
a
0
a+a
0
) = T r(1) = 1
(a, a
0
) T r(
a
a+a
0
) = 1 Tr(
a
0
a+a
0
) = 1
a 6= a
0
, a 6= 0, a
0
6= 0
T
2
(a, a
0
, b) =
X
z,y∈F
2
m
(−1)
T r(s(az)+s(a
0
z)+ay
P
t
i=0
((az)
2
i
+(az)
2
−i
)+a
0
y
P
t
i=0
((a
0
z)
2
i
+(a
0
z)
2
−i
)+bz)
=
= 2
m
g
X
(−1)
T r(s(az)+s(a
0
z)+bz)
,
f
P
a
t
X
i=0
((az)
2
i
+ (az)
2
−i
) + a
0
t
X
i=0
((a
0
z)
2
i
+ (a
0
z)
2
−i
) =
= a(az + T r(az)) + a
0
(a
0
z + T r(a
0
z)) = z(a
2
+ a
0
2
) + aT r(az) + a
0
T r(a
0
z) = 0,
F
2
m
z
{0,
1
a+a
0
} T r(
a
a+a
0
) = 1, T r(
a
0
a+a
0
) = 1
{0,
a
a
2
+a
0
2
} T r(
a
a+a
0
) = 1, T r(
a
0
a+a
0
) = 0
{0,
a
0
a
2
+a
0
2
} T r(
a
a+a
0
) = 0, T r(
a
0
a+a
0
) = 1
{0} T r(
a
a+a
0
) = 0, T r(
a
0
a+a
0
) = 0
T r(
a
a+a
0
) + T r(
a
0
a+a
0
) =
T r(
a
a+a
0
+
a
0
a+a
0
) = T r(1) = 1
{0,
a
a
2
+a
0
2
}
{0,
a
0
a
2
+a
0
2
}
{0,
a
a
2
+a
0
2
}

T
2
(a, a
0
, b) = 2
m
µ
1 + (−1)
T r
s(
a
2
a
2
+a
0
2
)+s(
aa
0
a
2
+a
0
2
)+
ab
a
2
+a
0
2
¶
.
¤
F
2
a, a
0
, b ∈ F
q
, a 6= a
0
, T r(s(ax) + s(a
0
x) + bx)
y = xA x = (x
1
, . . . , x
m
) A
T r(s(ax) + s(a
0
x) + bx) =
m−1
2
X
i=1
y
2i−1
y
2i
+ αy
m
, α ∈ F
2
.
m = 2t −1, t > 1 s(ax)
m = 2t − 1
K(m) n = 2
m+1
= 2
2t
Υ(a, b, ε, γ) = ( T r(s(ax) + bx + ε) |T r(s(ax) + (a + b)x + γ + ε) ), γ, ε ∈ F
2
, a, b ∈ F
2
2t−1
,
T r(s(ax) + bx + ε) T r(s(ax) + (a + b)x + γ + ε)
n
2
= 2
m
K(m)
K(m) Υ(a, b, ε, γ) +
Υ(a
0
, b
0
, ε
0
, γ
0
) K(m)
T r(s(ax)) + T r(s(a
0
x)) + bx + b
0
x
Υ(a, b, ε, γ) Υ(a, b, ε, γ)
T r(s((a + a
0
)x) + b
0
x + bx + b
00
x b
00
∈ F
2
m
a
a
0
T r(s((a + a
0
)x) + (a + a
0
)x + (b
0
+ b)x + b
00
x
m
K(m) n = 2
m+1

K(m) 4 · 2
2m
= n
2
d K(m) d = 2
m
− 2
1
2
(m−1)
=
1
2
(n −
√
n)
A(j) (Υ, Υ
0
) K(m) d(Υ, Υ
0
) =
j A(j) j = 0,
1
2
(n±
√
n), n
d(Υ, Υ
0
)
1
2
(n −
√
n)
n
2
1
2
(n +
√
n) n
(Υ, Υ
0
)
d(Υ, Υ
0
)
n
2
1
2
n
3
(n −2) 2n
3
−2n
2
1
2
n
3
(n −2) n
2
K(m)
d =
1
2
(n −
√
n)
(Υ(a, b, ε, γ), Υ(a
0
, b
0
, ε
0
, γ
0
)), (a, b, ε, γ) 6= (a
0
, b
0
, ε
0
, γ
0
), K(m)
0 ±2
m
2
a 6= a
0
a 6= 0, a
0
6= 0 T r(
a
a+a
0
) + T r(
a
0
a+a
0
) = T r(1) = 1
T r(
a
a+a
0
) = 1
(T r(s(ax) + bx + ε), T r(s(a
0
x) + b
0
x + ε
0
) = (−1)
ε+ε
0
T (a, a
0
, b + b
0
)
(T r(s(ax) + (a + b)x + γ + ε)), Tr(s(a
0
x) + (a
0
+ b
0
)x + γ
0
+ ε
0
)) =
= (−1)
ε+ε
0
+γ+γ
0
T (a, a
0
, b + b
0
+ a + a
0
)
0 2
t
= 2
m+1
2
T r
µ
a(b + b
0
)
a
2
+ a
0
2
¶
+ T r
µ
a(a + a
0
+ b + b
0
)
a
2
+ a
0
2
¶
= T r
µ
a(a + a
0
)
a
2
+ a
0
2
¶
= T r
µ
a
a + a
0
¶
= 1
T (a, a
0
, b + b
0
) = 0, T (a, a
0
, b + b
0
+ a + a
0
) = ±2
t
T (a, a
0
, b + b
0
) =
±2
t
, T (a, a
0
, b + b
0
+ a + a
0
) = 0
|T (a, a
0
, b + b
0
) ± T (a, a
0
, b + b
0
+ a + a
0
)| = 2
t
.
a 6= 0, a
0
= 0 a
0
6= 0, a = 0
