Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

21.2. ОТКРЫТОЕ УПРАВЛЕНИЕ И ЭКСПЕРТНЫЙ ОПРОС

На первый взгляд кажется, что наилучшее решение здесь — взять

в качестве итогового решения среднее арифметическое мнений экс-

пертов

Однако у такого решения есть существенный недостаток.

Дело состоит в следующем. У каждого эксперта есть мнение

Т{

относительно объема финансирования. И если эксперт каким-либо

образом заинтересован в том, чтобы итоговая оценка х совпала с

его мнением

Г{,

то он может попытаться добиться этого совпадения,

сообщая оценку

г.

Пример 5. Пусть три эксперта имеют следующие мнения:

Если каждый из них сообщит свое мнение без искажений, то при

принятии решения по способу (4) результат будет таким:

Однако третий эксперт может (имея представление о мнениях

остальных двух экспертов) сообщить оценку

5з

= 100. Тогда итого-

вый результат

как раз совпадет с его истинным мнением

Замечание. В теории коллективного принятия решений такой спо-

соб действий называется манипулированием. В свою очередь, если

механизм коллективного принятия решений допускает манипулиро-

вание с чьей-либо стороны, то он называется манипулируемым. Рас-

смотренный только что пример показал, что механизм (4) являет-

ся манипулируемым: искажая свои истинные предпочтения, можно

приблизить итоговое коллективное решение к собственному истин-

ному предпочтению.

Пример манипулирования со стороны избирателей можно было

наблюдать в первом туре президентских выборов в России в 1996 г.

Определенное число избирателей, считавших лучшей кандидатурой

Явлинского, голосовали за Ельцина (с целью предотвратить победу

Зюганова).

411

ГЛАВА 21. УПРАВЛЕНИЕ ОРГАНИЗАЦИОННЫМИ СИСТЕМАМИ

Вернемся к экспертному опросу. Говоря более строго, г-й эксперт

решает задачу

т. е. пытается минимизировать разность между итоговым решением

х и своим истинным мнением

г г

путем надлежащего выбора сообща-

емой оценки

S{.

Опишем механизм выработки решения

х*,

являющийся механиз-

мом открытого управления (т. е. неманипулируемым механизмом).

Напомним, что эксперты сообщают свои оценки

Будем считать, не ограничивая общности, что оценки экспертов рас-

положены по неубыванию:

(этого всегда можно добиться перенумерацией экспертов).

Вычисляются п вспомогательных чисел

(эти числа делят отрезок

[d,

D] на п равных частей). После этого

для каждого

берется меньшее из двух чисел

И наконец, из всех этих минимумов выбирается наибольший, кото-

рый и является итоговым решением:

Можно доказать, что описанный механизм является механизмом

открытого управления.

Пример 6. Пусть 6 экспертов сообщили следующие оценки из

промежутка [30, 90]: 65, 90, 45, 80, 75, 90. Определить итоговое реше-

ние в соответствии с описанным механизмом.

Решение. Выпишем числа

(здесь

412

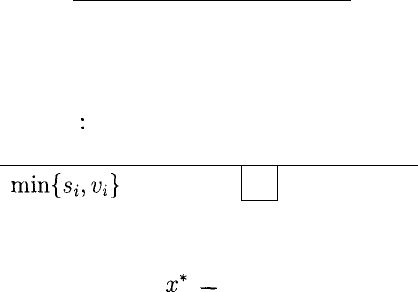
21.3. ЗАДАНИЯ И ОТВЕТЫ

Дальнейшее удобно изобразить в виде таблицы, в первой строке ко-

торой записаны упорядоченные по неубыванию оценки экспертов:

Si :

min{si,Vi}

: 45

В качастве итогового решения берется максимальное число в послед-

ней строке:

х*

~ 70.

Замечание. Во всех предыдущих рассуждениях квалификация экс-

пертов предполагается одинаковой. Можно в случае необходимо-

сти вводить коэффициенты, позволяющие учитывать мнение раз-

ных экспертов различным образом — принципиально это ничего не

меняет, лишь несколько усложняется вычисление итогового резуль-

тата X*.

21.3. Задания и ответы

1. Восемь Потребителей подали Центру заявки в размере 9, 18, 15,

14, 10, 13, 7, 14. Имеющийся в распоряжении Центра ресурс соста-

вляет 70. Как должен быть распределен этот ресурс в соответствии

с механизмом прямых приоритетов?

Ответ: 6,3; 12,6; 10,5; 9,8; 7; 9,1; 4,9; 9,8.

2. Распределение ресурса производится в соответствии с механиз-

мом обратных приоритетов. Приоритеты четырех Потребителей

определяются числами 26, 18, 24, 20. Какими являются равновесные

стратегии (заявки) Потребителей, если имеющийся в распоряжении

Центра ресурс составляет 50?

Ответ: 13,6; 11,3; 13,1; 11,9.

3. Распределение ресурса осуществляется в соответствии с кон-

курсным механизмом. Пять Потребителей сообщили Центру свои

заявки: 5, 8, 6, 9, 8 и показатели эффекта: 12, 21, 18, 23, 23 соот-

ветственно. Как должен быть распределен между Потребителями

ресурс объемом 25?

Ответ: 0; 8; 6; 0; 8.

413

ГЛАВА 21. УПРАВЛЕНИЕ ОРГАНИЗАЦИОННЫМИ СИСТЕМАМИ

4. Восемь Потребителей подали Центру заявки 13, 10, 16, 19, 9,

12, 14, 11. Центр располагает ресурсом объемом 100. Как должен

быть распределен этот ресурс в соответствии с механизмом откры-

того управления?

Ответ: 13; 10; 15,5; 15,5; 9; 12; 14; 11.

5. Восьми экспертам было предложено сообщить оценку объема

финансирования из промежутка [0, 80]. Эксперты сообщили следую-

щие оценки: 45, 10, 35, 80, 65, 35, 60, 55. Определите итоговое решение

при помощи механизма открытого управления.

Ответ: 45.

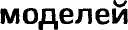
Глава 22

ДИНАМИЧЕСКИЕ МОДЕЛИ

Модель — это представление объекта, системы

или идеи в некоторой форме, отличной от самой

целостности.

Р.Шеннон

22.1. Коротко о типах

моделей

Не ставя перед собой задачи дать сколько-нибудь полную классифи-

кацию существующих моделей, коротко опишем некоторые их типы.

22.1.1. Физические модели

Так называют увеличенное или уменьшенное описание объекта или

системы. Отличительная характеристика физической модели состо-

ит в том, что в некотором смысле она выглядит как моделируемая

целостность.

Наиболее известным примером физической модели является ко-

пия конструируемого самолета, выполненная с полным соблюдени-

ем пропорций, скажем 1 : 50. На одном из этапов разработки са-

молета новой конструкции возникает необходимость проверить его

основные аэродинамические параметры. С этой целью подготовлен-

ную копию продувают в специальной (аэродинамической) трубе, а

полученные показания затем тщательно исследуют. Выгодность та-

кого подхода совершенно очевидна. И потому все ведущие самолето-

строительные компании используют физические модели подобного

рода при разработке каждого нового летательного аппарата.

Часто в аэродинамическую трубу помещают уменьшенные копии

многоэтажных зданий, имитируя при этом розу ветров, характерную

для той местности, где предполагается их строительство. Пользуют-

ся физическими моделями и в кораблестроении.

415

ГЛАВА 22. ДИНАМИЧЕСКИЕ МОДЕЛИ

22.1.2. Аналоговые модели

Так называют модели, представляющие исследуемый объект анало-

гом, который ведет себя как реальный объект, но не выглядит как

таковой.

Приведем два достаточно характерных примера.

Пример 1. График, иллюстрирующий соотношения между за-

траченными усилиями и результатами, является аналоговой моде-

лью. График на рис. 1 показывает, как количество времени, отведен-

ное студентом на подготовку к экзамену, влияет на его результат.

Рис. 1

Пример 2. Предположим, что нужно найти наиболее экономич-

ный способ для регулярных известных поставок товаров в три го-

рода, построив для этого только один склад. Основное требование:

место для склада должно быть таким, чтобы полные транспортные

расходы были наименьшими (считается, что стоимость каждой пе-

ревозки равна произведению расстояния от склада до пункта на-

значения на общий вес перевозимых товаров и измеряется в тонна-

километрах).

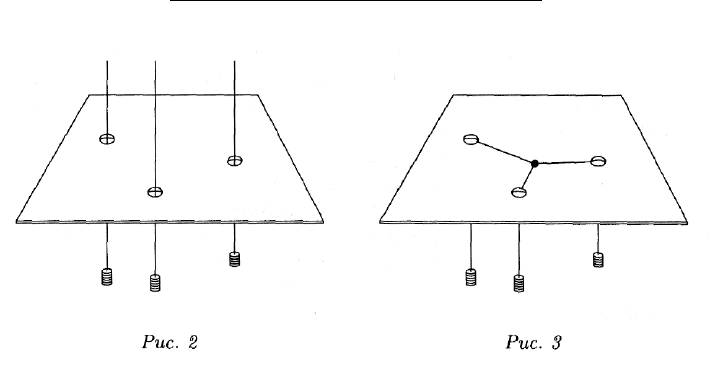
Наклеим карту местности на лист фанеры. Затем в месте нахо-

ждения каждого города пропилим

сквозные

отверстия, пропустим

через них нити и привяжем к ним грузики, пропорциональные запро-

сам товаров в этот город (рис. 2). Свяжем свободные концы нитей в

один узел и отпустим. Под действием силы тяжести система придет

416

22.1. КОРОТКО О ТИПАХ МОДЕЛЕЙ

в состояние равновесия. То место на листе фанеры, которое при этом

займет узел, и будет соответствовать оптимальному расположению

склада (рис. 3).

Замечание. Стоимость дорог, которые придется построить заново,

мы для простоты рассуждений в расчет не принимаем.

22.1.3. Математические модели

Так называют модели, использующие для описания свойств и харак-

теристик объекта или события математические символы и методы.

Если некоторую проблему удается перенести на язык формул, то

она сильно упрощается. Математический подход прост еще и потому,

что он подчиняется вполне определенным жестким правилам, кото-

рые нельзя отменить указом или иным способом. Сложность нашей

жизни как раз и состоит в том, что многое, что в ней случается,

нередко свободно от пут условностей.

Математика имеет дело с упрощенным описанием явлений. По

существу, любая формула (или совокупность формул) представля-

ет собой определенный этап в построении математической модели.

Опыт показывает, что построить модель (написать уравнение) до-

вольно легко. Трудно в этой модельной и, следовательно, упрощен-

ной форме суметь передать суть изучаемого явления.

Для нахождения приемлемого или оптимального решения зада-

чи полезно знать, в чем она состоит. Как ни просто и прозрачно

данное утверждение, чересчур многие < ... > игнорируют оче-

видное (Р. Шеннон).

417

ГЛАВА 22. ДИНАМИЧЕСКИЕ МОДЕЛИ

В предыдущих главах мы рассмотрели достаточное число разно-

образных математических моделей, детерминированных, стохасти-

ческих и игровых. В этой главе мы приведем примеры динамических

моделей, на основании которых можно делать прогнозы на будущее

и по-новому заглядывать в прошлое.

Итак, мы рассматриваем модели, в которые входят изменяющиеся

во времени величины, уделяя основное внимание простейшим из них.

Дело в том, что сами модельные уравнения (модели) строятся на

основе простых и зачастую почти очевидных соображений. Именно

анализ предлагаемых уравнений позволяет как-то оценить степень

их адекватности описываемым ими обстоятельствам.

22.2. Модель народонаселения

Интересно, что построить математическую модель часто совсем

не-

трудно. Нередко для этого используются самые простые и легкообъ-

яснимые предположения.

Опишем, как это можно сделать, на одном почти реальном при-

мере.

Представим себе следующую картину.

Середина

XVIII в. Цент-

ральная Европа, Приход в глубинке. Церковь. Прихожане — жите-

ли окрестных деревень. Приходский священник замечает, что храм

стал тесноват для богослужений: возросло число прихожан. Свя-

щенник размышляет: если число прихожан будет увеличиваться и в

будущем, то придется строить новую церковь, для чего понадобятся

средства, и немалые.

Священик понимает, что срок, за который должен быть построен

храм, и его размеры во многом зависят от того, как именно будет

изменяться число окрестных жителей. И он решает попытаться рас-

считать

это.

Попробуем и мы изложить возможный ход его рассуждений, поль-

зуясь современными обозначениями и языком.

Обозначим через

количество прихожан к концу n-го года. Их

численность через год, т. е. к концу (п + 1)-го года, естественно обо-

значить через

х.п+1-

Тогда изменение численности за этот год можно

описать разностью

Оно происходит по двум естественным причинам — люди рождают-

ся и умирают (для простоты будем считать, что вирус миграций эту

418

22.2. МОДЕЛЬ НАРОДОНАСЕЛЕНИЯ

местность тогда еще не поразил). Определить число родившихся и

число умерших за год по приходским книгам особого труда не соста-

вляет. Подсчитывая число родившихся и умерших в разные годы,

священник решает сопоставить полученные числа

d\,.

• •

с общим числом прихожан за эти годы

,..

.,х

и замечает, что отношения

. ) • • • !

год от года различаются весьма мало. То же касается и отношений

419

ГЛАВА 22. ДИНАМИЧЕСКИЕ МОДЕЛИ

Тогда интересующая

нас

формула примет вид

%п+1

—

п-

(1)

Модель построена.

Попробуем теперь разобраться с тем, что же получилось, т. е. про-

анализировать построенную модель.

Возможны три случая:

—

ft >

—

рождается

больше, чем умирает) и

численность прихожан растет год от года,

a—j3

= 0 — умирает столько же, сколько рождается)

и численность прихожан год от года остается неизменной,

< 0 -

умирает больше, чем рождается) и

численность прихожан неуклонно снижается.

Так как побудительным мотивом для построения модели было

желание узнать, как быстро будет расти число прихожан, начнем с

рассмотрения случая 1.

Случай 1.

Итак,

численность прихожан растет. Но как, насколько

быстро?

Здесь самое время кратко вспомнить поучительную историю (пе-

чальную притчу) о безвестном изобретателе шахмат.

Говорят, что игра очень понравилась богатому и всесильному ма-

гарадже, который тут же решил наградить изобретателя и щедро

предложил выбрать вознаграждение ему самому. Тот, как рассказы-

вают, смахнув фигуры с шахматной доски, положил на 1-ю клетку

одно пшеничное зернышко,

на

2-ю

два зернышка, на 3-ю — че-

тыре зернышка,

на

4-ю - восемь зернышек (рис. 4) и предложил

магарадже, чтобы он отдал распоряжение слугам выкладывать зер-

на пшеницы

на

другие клетки шахматной доски по предложенному

Рис.

420