Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

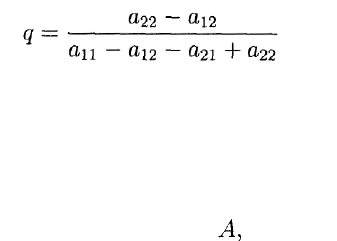
19.5. НЕКОТОРЫЕ ИТОГИ

(и не зависит от элементов его собственной платежной матрицы),

а выбор игрока В в равновесной ситуации полностью определяется

элементами платежной матрицы игрока А,

(и не зависит от элементов его собственной платежной матрицы).

Иными словами, равновесная ситуация обоих игроков определя-

ется не столько стремлением увеличить собственный выигрыш,

сколько желанием держать под контролем выигрыш другого игрока

(минимизировать этот выигрыш). И если, например, заменить в би-

матричной игре матрицу выплат игроку

А,

а матрицу выплат игроку

В оставить прежней, то игрок А никак не изменит своего "равновес-

ного" поведения (просто не обратит внимания на эту замену), в то

время как игрок В изменит свою стратегию на новую, равновесную.

Таким образом, в биматричной (неантагонистической) игре мы

вновь встречаемся с антагонизмом. Правда, теперь это уже не анта-

гонизм интересов (как было в антагонистической, матричной игре),

а антагонизм поведения.

Отметим, что в биматричными играх (в отличие от матричных)

при наличии нескольких ситуаций равновесия средний выигрыш иг-

рока в разных равновесных ситуациях различен (напомним, что в

матричной игре выигрыш игрока один и тот же вне зависимости от

количества точек равновесия).

Но если средние выигрыши разнятся, то какую равновесную си-

туацию следует считать оптимальной?

Наконец, еще одно, не менее интересное обстоятельство. Вспо-

мним, с какими трудностями мы столкнулись, пытаясь перевести

эмоциональные оценки результатов общения студент - преподава-

тель в количественные показатели. В целом сохраняя основные со-

отношения, эти количественные оценки могут, конечно, изменяться

как от студента к студенту, так и от преподавателя к преподавате-

лю. Однако если эти изменения будут не слишком значительными —

элементы платежной матрицы "пошевельнутся" слегка — то слег-

ка "пошевельнутся" и зигзаги, не изменяя ни своей общей формы,

ни взаимного расположения, а значит, число равновесных ситуаций

не изменится. Впрочем, сказанное относится лишь к случаю, когда

множество ситуаций равновесия конечно и состоит из нечетного чи-

сла точек (одной или трех).

391

ГЛАВА 19. БИМАТРИЧНЫЕ ИГРЫ

Как принято говорить в подобных случаях, это число устойчиво

относительно малых шевелений.

Конечно, в некоторых биматричных играх равновесные ситуации

случаются и в чистых стратегиях (в последнем из разобранных при-

меров таких ситуаций даже две). И (в принципе, это совсем нетруд-

но) можно дать определение ситуации равновесия в чистых страте-

гиях. Найти ее (если она, конечно, существует) — дело довольно

простое. Но, как показывают разобранные примеры, во-первых, чи-

стой ситуации равновесия может вовсе не быть, и, во-вторых, даже

при ее наличии не исключено существование равновесных ситуаций

в смешанных стратегиях. И, чтобы найти их все, неизбежно прихо-

дится обращаться к описанному выше подходу.

19.6. Задания и ответы

Глава 20

НЕКОТОРЫЕ ДРУГИЕ ИГРЫ

Реальные конфликтные ситуации приводят к различным видам игр.

К настоящему времени общепризнанной классификации игр не сло-

жилось. Тем не менее легко заметить, что игры можно различать по

целому ряду признаков: по количеству участвующих в них игроков,

возможных стратегий, ходов, по характеру взаимоотношений между

игроками, выигрышей, информационной обеспеченности игроков, по

виду функций выигрышей и т. д.

В зависимости от вида игры разрабатывается и метод ее решения.

В этой главе мы приведем примеры игр, отличных от рассмотрен-

ных ранее. Но начнем с обсуждения (на примере биматричной игры)

несколько иного подхода к вопросу устойчивости искомой ситуации.

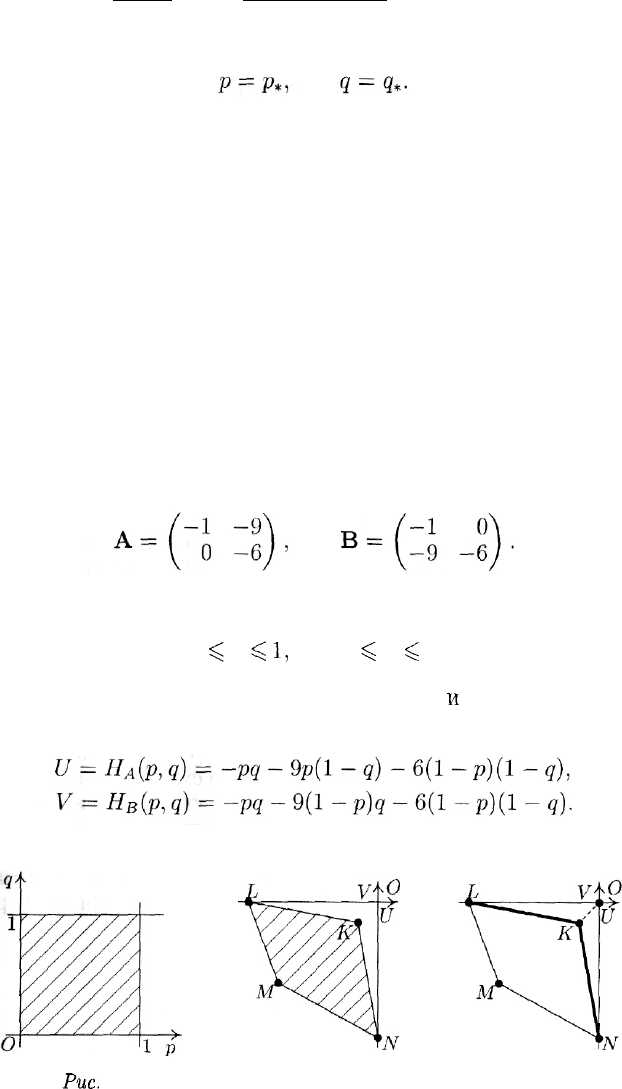
ГЛАВА 20. НЕКОТОРЫЕ ДРУГИЕ ИГРЫ

вытекает, что

Иными словами, в оптимальной по Парето ситуации игроки не

могут совместными усилиями увеличить выигрыш одного из них, не

уменьшив при этом выигрыш другого.

Отличие ситуации равновесия от ситуации, оптимальной по Па-

рето, состоит в следующем:

в ситуации равновесия ни один из игроков, действуя в одиночку,

не может увеличить свой собственный выигрыш;

в ситуации, оптимальной по Парето, игроки, действуя совместно,

не могут увеличить выигрыш хотя бы одного из них, не уменьшая

выигрыша другого.

Покажем, как практически отыскиваются оптимальные по Паре-

то ситуации.

Обратимся к игре "Дилемма узников".

Напомним, что соответствующие платежные матрицы в этой игре

имеют следующий вид:

Тем самым на единичном квадрате

(рис. 1) возможных значений вероятностей р

q заданы две функ-

ции:

Рис.

Рис. 2

Рис. 3

394

20.2. НЕАНТАГОНИСТИЧЕСКИЕ ПОЗИЦИОННЫЕ ИГРЫ

Точки с координатами (U,V), вычисленными по приведенным

формулам, на плоскости (U, V) заполняют четырехугольник с вер-

шинами

К{-1,

-1),

L(-9,0),

М(-6,

-6) и N(0, -9) (рис. 2). Граница

Парето этого множества — ломаная

NKL.

В качестве точки утопии здесь естественно рассматривать началь-

ную точку

О(0,

0). Идеальная точка К(—1,

—1)

— точка с наиболь-

шими выигрышами для каждого из игроков — оказывается лучше,

чем равновесная (рис. 3). Ей соответствуют чистые стратегии обоих

игроков

20.2. Неантагонистические позиционные игры

Мы достаточно подробно остановились на позиционных играх двух

лиц, где были явно выражены интересы одного из игроков (игро-

ка А). Следует, однако, иметь в виду, что в одних случаях интересы

игрока В могут быть полностью противоположными интересам игро-

ка

А,

в то время как в других вполне может оказаться, что то, что

хорошо для одного игрока, необязательно плохо для другого.

Приведем два простых примера.

Пример 1. 1-й ход. Игрок А выбирает число х из множества

двух чисел {1,2}.

2-й ход. Игрок В выбирает число у из множества двух чисел {1,2},

зная выбор числа х игроком А.

Функции выплат игрокам

—

WA(X,H)

\¥в(х,у)

соответ-

ственно — задаются так:

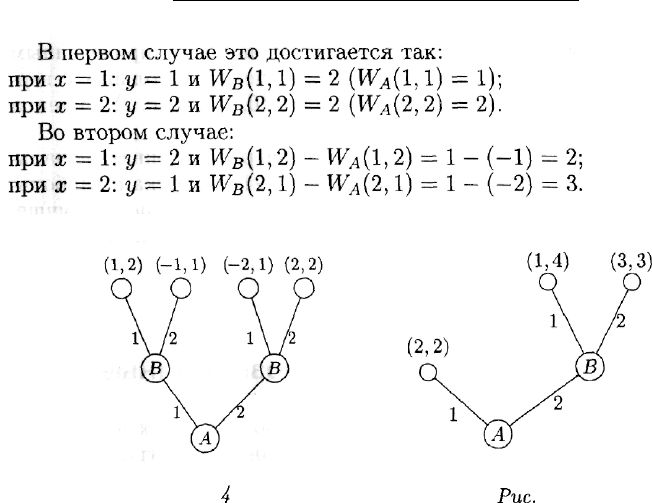
Дерево игры показано на рис. 4.

Исход игры зависит от того, каковы намерения игрока В —

максимизировать свой выигрыш:

или

максимизировать свой относительный выигрыш:

395

ГЛАВА 20. НЕКОТОРЫЕ ДРУГИЕ ИГРЫ

Рис.

Пример 2. Игра задается деревом (рис. 5).

1-й ход. Игрок А выбирает число х из множества двух чисел {1, 2}.

Если х = 1, то каждый из игроков получает свой выигрыш, рав-

ный 2.

Если х = 2, то игрок В получает право 2-го хода, где он и выби-

рает число у из множества двух чисел {1,2}.

При у = 1 выигрыш игрока А равен 1, а игрока В — 4. При у = 2

оба игрока получают поровну — по 3.

В случае когда каждый из игроков стремится к получению мак-

симального выигрыша и любые виды кооперации запрещены, исход

игры ясен — игрок А выбирает х = 1 и игра заканчивается. Но при

х = 2 и у = 2 каждый из игроков получает по 3 (такой исход предпо-

чтительнее простейшего (2,2)), и, если допустить соглашение между

игроками, это обстоятельство вполне может изменить исход игры.

20.3. Бесконечные игры

Выше мы остановились достаточно подробно лишь на трех видах

игр — матричных, позиционных и биматричных. Сделанный вы-

бор обусловлен тем, что уже здесь можно наглядно показать, ка-

396

20.3. БЕСКОНЕЧНЫЕ ИГРЫ

кой смысл вкладывается в термин игра и чем именно занимается

теория игр, а также познакомить с относительно несложным мате-

матическим инструментарием, опирающимся на ключевые понятия

вероятности, матрицы и координаты и позволяющим разрешать про-

стейшие из этих видов игр.

Вместе с тем нам не хотелось бы, чтобы у читателя сложилось

впечатление, что доступными содержательному анализу могут быть

только игры, описанные выше.

Существует интересный, привлекающий неослабевающее внима-

ние исследователей класс игр, в которых хотя бы один из игроков

имеет бесконечное множество возможных стратегий, — бесконечные

игры.

В этом заключительном разделе мы приведем примеры бесконеч-

ных игр двух лиц трех видов — непрерывной игры на единичном

квадрате (непрерывными называются бесконечные игры, в которых

функции выигрышей непрерывно зависят от стратегий, выбираемых

игроками), дуэли (играми с выбором момента времени, или играми

типа дуэли, называются игры, характеризующиеся моментом вы-

бора хода и вероятностями получения выигрыша в зависимости от

времени, прошедшего от начала игры до момента выбора) и диффе-

ренциальной игры поиска (в дифференциальных играх допускается

делать ходы непрерывно и связывать поведение игроков условиями,

описываемыми дифференциальными уравнениями).

Мы ограничимся здесь лишь постановками задач — описанием

возможностей в поведении игроков и построением функций выигры-

шей, хотя для каждой из приводимых игр разработаны достаточно

эффективные подходы к построению их решения.

20.3.1. Борьба за рынки (игра на единичном квадрате)

Одна из конкурирующих фирм (игрок А) пытается вытеснить дру-

гую фирму (игрок В) с одного из двух рынков сбыта. Предположим,

что общая сумма средств, выделенная на это игроком А, равна 1. Ти-

пичной стратегией игрока А является разделение выделенной суммы

на две части: х (0

1) для первого рынка и 1 — х для второго.

Подобным образом выглядят и стратегии игрока

В:

выделение им

части у (0

1) своей суммы на первый рынок и 1 — у на второй.

Будем считать, что если игрок А добился превосходства на од-

ном из рынков (на другом превосходства автоматически добивается

игрок В), то он вытесняет противника с этого рынка и получает

выигрыш, пропорциональный избытку вложенных средств с коэф-

397

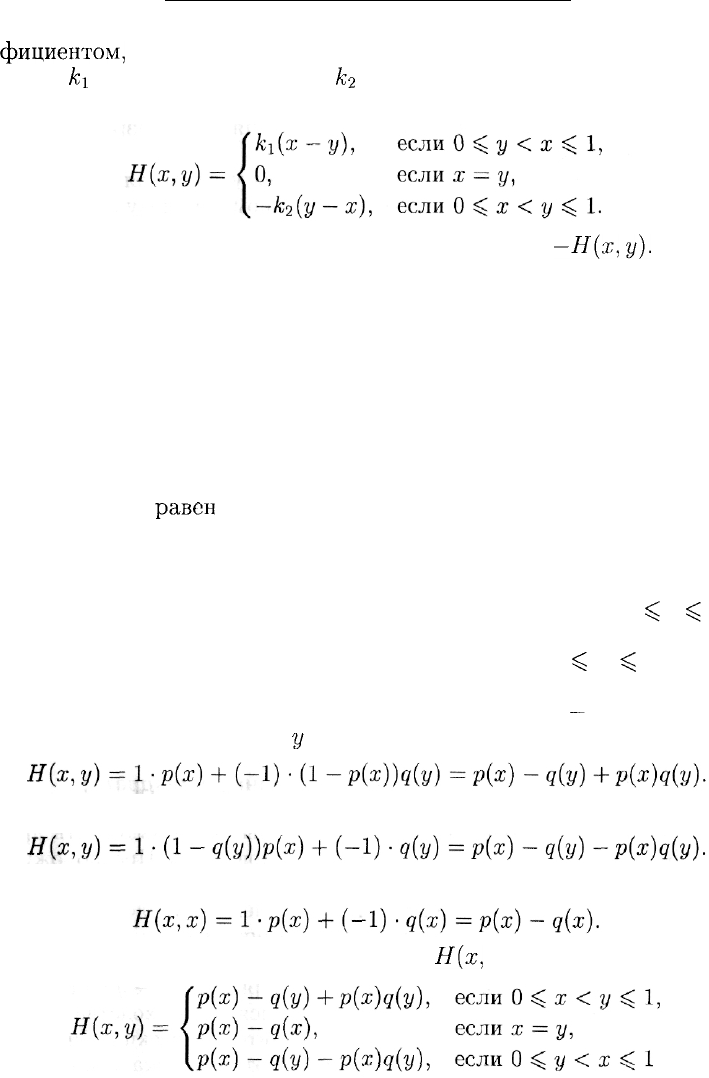
ГЛАВА 20. НЕКОТОРЫЕ ДРУГИЕ ИГРЫ

фициентом,

характеризующим важность рынка (этот коэффициент

равен

к\

для первого рынка и

А;

для второго). Тогда функция вы-

игрыша Н(х, у) игрока А определяется формулой

Ясно, что функция выигрыша игрока В равна

—Н(х,у).

20.3.2. Игра типа дуэли

Два дуэлянта (игроки А и В) начинают сходиться в момент време-

ни t = 0. У каждого пистолет заряжен одной пулей. Они встретятся

в момент времени t = 1 (если только ни один из них не застрелит

другого раньше). Каждый из дуэлянтов может выстрелить, когда

пожелает. Если при этом одному из них удастся поразить против-

ника, а самому остаться невредимым, то он становится победителем

(его выигрыш

равен

1) и дуэль тут же прекращается. Если оба про-

махнутся, дуэль закончится вничью (выигрыш каждого из игроков

равен 0). Если оба выстрелят одновременно и каждый поразит про-

тивника, то дуэль также считается окончившейся вничью.

Если игрок А произведет выстрел в момент времени х (0

1),

то его выстрел будет успешным с вероятностью р(х). Подобным же

образом выстрел игрока В в момент времени у (0

1) будет

успешным с вероятностью q(y). При условии х < у игрок А выиграет

с вероятностью р(х), а проиграет с вероятностью (1

—

p(x))q(y). Его

средний выигрыш при х <

будет равен

С другой стороны, если х > у, его средний выигрыш будет равен

При х = у средний выигрыш

Таким образом, функция выигрыша

Н(х,

у) игрока А имеет вид

и антагонистическая игра задана.

398

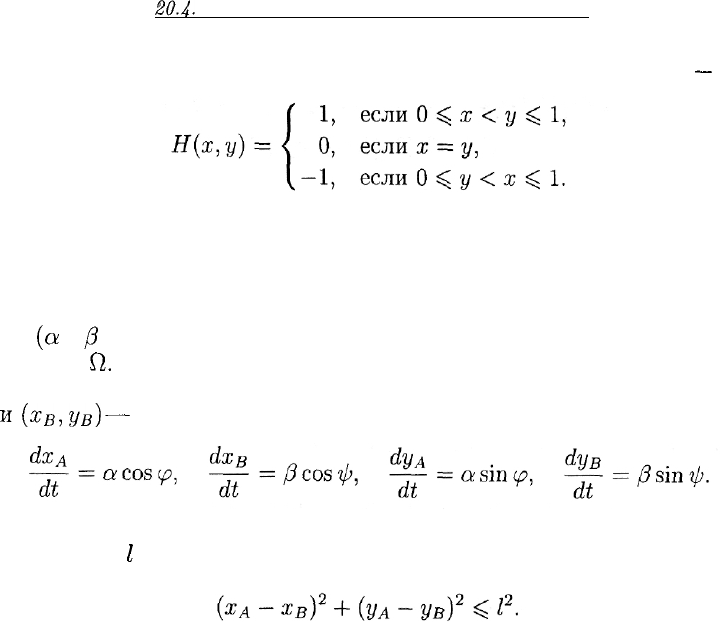
20.1

НЕСКОЛЬКО СЛОВ В ЗАКЛЮЧЕНИЕ

В частности, если игроки стреляют без промаха, р(х) — q(y)

20.3.3. Дифференциальная игра поиска

Ищущий (игрок А) стремится обнаружить уклоняющегося (игрок

В). Оба игрока перемещаются с постоянными скалярными скоростя-

ми

(а

соответственно) по плоскости внутри некоторой поисковой

области

П.

В любой момент каждый из игроков управляет своим пе-

ремещением, задавая направление вектора скорости. Пусть

(ХА,УА)

{хв,Ув)

—

координаты игроков. Тогда имеем

Игра поиска заканчивается в тот момент, когда игроки сблизятся на

расстояние

> О, иными словами, когда будет выполнено неравен-

ство

В случае успешного обнаружения выигрыш игрока А считается рав-

ным 1.

Построение решения в этой игре существенно зависит от харак-

тера и степени информированности игроков.

20.4. Несколько слов в заключение

Все это были примеры бескоалиционных игр, когда любые согла-

шения, обмен информацией, побочные платежи, совместный выбор

стратегий запрещены. Другой важный класс составляют коопера-

тивные игры, в которых разрешены самые разнообразные формы

сотрудничества (что особенно важно при наличии числа игроков,

большего двух). Возможность соглашений между игроками оказыва-

ет существенное влияние на исход игры. Если допустить, например,

в игре "Дилемма узников" совместный выбор стратегий, то исход

игры может оказаться совсем иным. При наличии побочных плате-

жей по-иному окончится и "Семейный спор".

Глава 21

УПРАВЛЕНИЕ ОРГАНИЗАЦИОННЫМИ

СИСТЕМАМИ

21.1. Распределение ресурсов

21.1.1. Постановка задачи распределения ресурсов

Организационная система (оргсистема, организация) — это система,

включающая технику и коллективы людей, интересы которых суще-

ственно связаны с ее функционированием. Примерами здесь могут

служить семья, фирма, университет, город, страна. Каждая оргси-

стема состоит из элементов (которые в свою очередь тоже могут

представлять собой системы).

Для нас существенными являются следующие два обстоятель-

ства. С одной стороны, система существует для достижения каких-

либо определенных целей, т. е. можно говорить об интересах системы

в целом. С другой стороны, элементы системы зачастую преследуют

собственные интересы, вообще говоря не совпадающие с интересами

системы в целом. Все это дает основание формализовать некоторые

аспекты функционирования оргсистем в терминах теории игр.

В данном разделе мы будем рассматривать простейшую двухуров-

невую модельную оргсистему, состоящую из Центра и некоторого

числа однотипных Элементов. Управление такой системой мы рас-

смотрим на примере задачи распределения ресурсов. Суть этой за-

дачи состоит в следующем. Элементы (в дальнейшем мы будем на-

зывать их Потребителями) представляют Центру заявки на полу-

чение некоторого ресурса (для простоты рассматривается один вид

ресурса). Центр на основании этих заявок распределяет имеющий-

ся в его распоряжении ресурс (который предполагается делимым).

400