Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

19.4-

ПОИСК РАВНОВЕСНЫХ СИТУАЦИЙ

пара

(р,

q) определяла равновесную ситуацию, необходимо и доста-

точно одновременное выполнение следующих неравенств:

где

19.4. Поиск равновесных ситуаций

Геометрический смысл условий (3) рассмотрим на примерах описан-

ных выше биматричных игр.

19.4.1. Борьба за рынки

Напомним, что ситуация, сложившаяся в этой задаче, задается пла-

тежными матрицами следующего вида:

ГЛАВА 19. БИМАТРИЧНЫЕ ИГРЫ

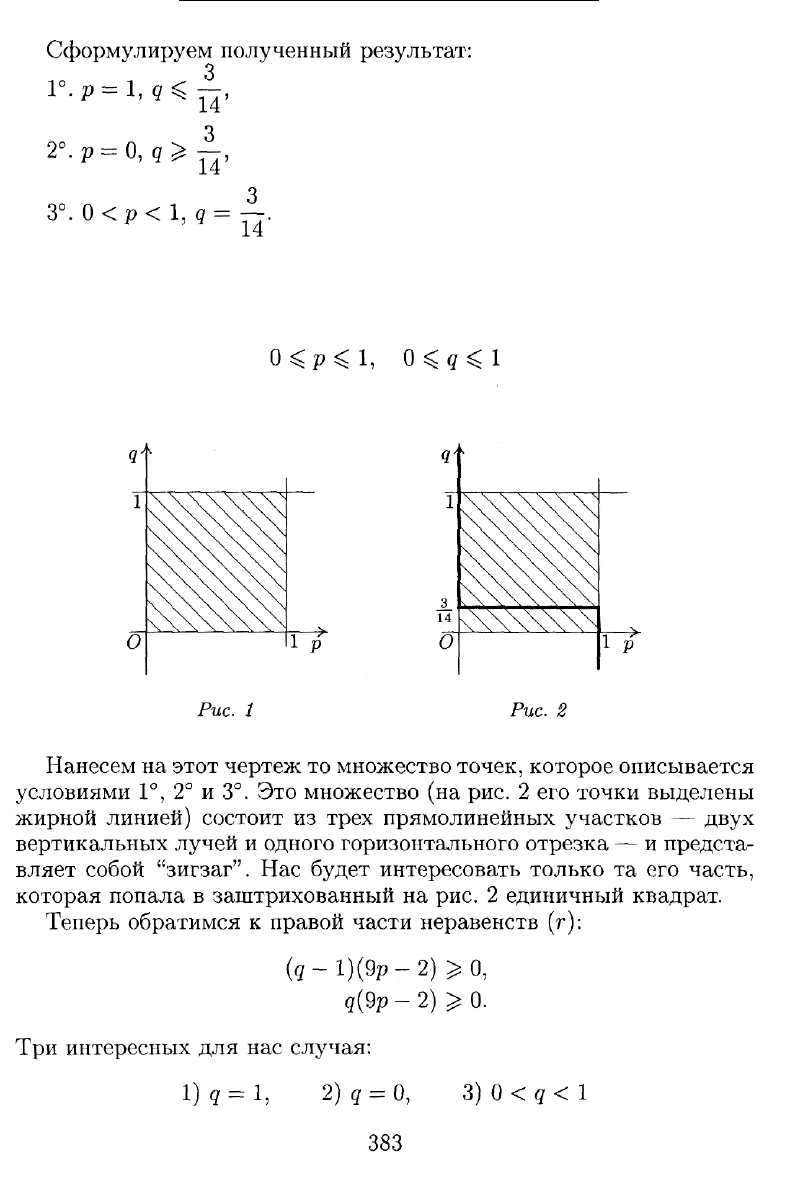
Рассмотрим сначала левую пару неравенств (7):

19.4. ПОИСК РАВНОВЕСНЫХ СИТУАЦИЙ

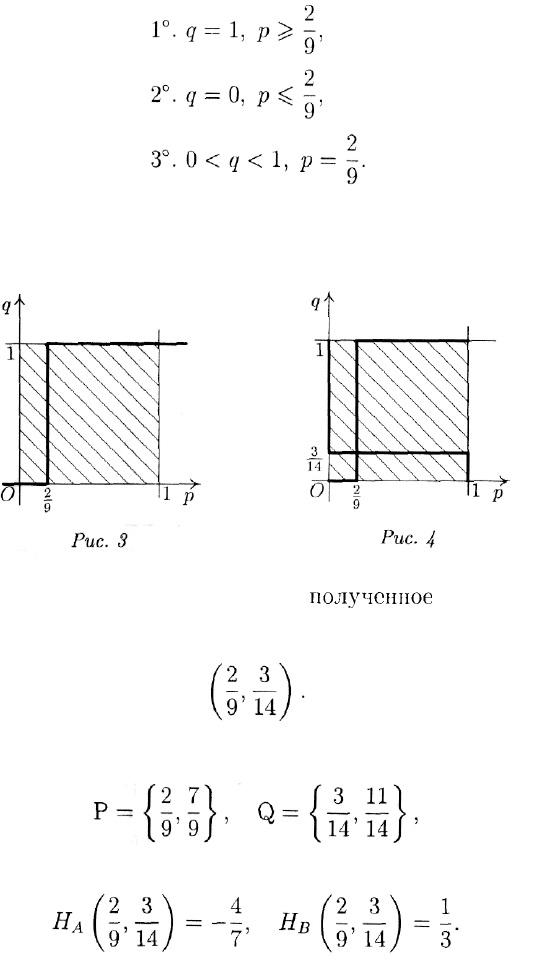
Перенесем теперь полученные результаты на чертеж.

Введем на плоскости прямоугольную систему координат (р, q) и

выделим на ней единичный квадрат, соответствующий неравенствам

(рис. 1).

ГЛАВА 19. БИМАТРИЧНЫЕ ИГРЫ

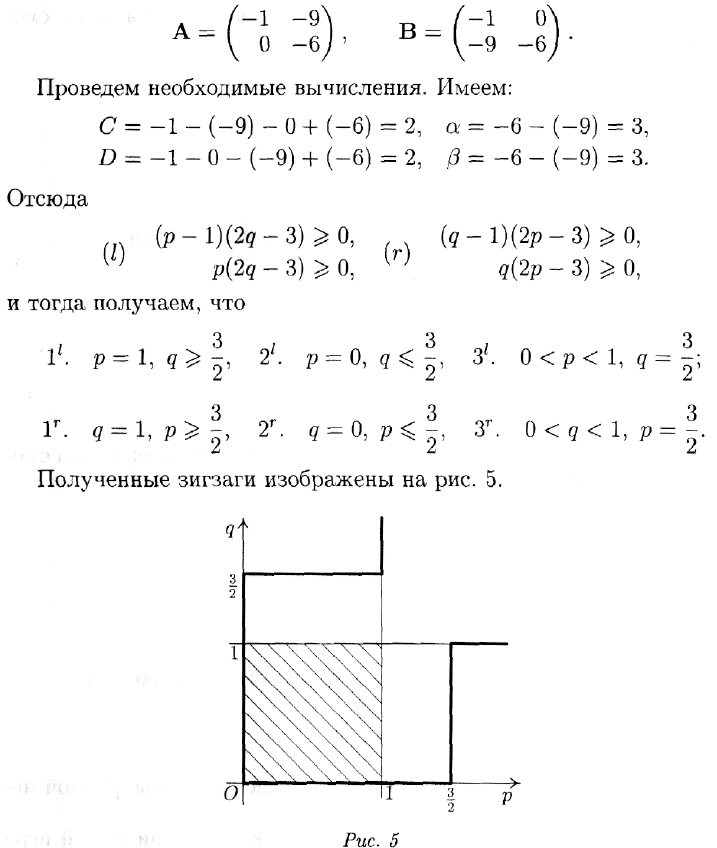
приводят к следующему результату:

Перенося его на чертеж, получим второй "зигзаг", но уже гори-

зонтальный (рис. 3).

Теперь остается только объединить

полученное

на рис. 4.

Общая точка построенных зигзагов — точка равновесия — имеет

координаты

Соответствующие смешанные стратегии игроков имеют следую-

щий вид:

а средние выигрыши игроков таковы:

Замечание. Попробуем разбить рассмотренную биматричную игру

на две матричные игры с нулевой суммой.

384

ГЛАВА 19. БИМАТРИЧНЫЕ ИГРЫ

19.4.2. Дилемма узников

Выигрыши игроков А ТА В описываются соответствующими матри-

цами выплат:

Единственная равновесная ситуация — (0,0). Это ситуация, в ко-

торой каждый из игроков выбирает вторую чистую стратегию —

сознаться — и его потери составляют 6.

386

19.1

ПОИСК РАВНОВЕСНЫХ СИТУАЦИЙ

ГЛАВА 19. БИМАТРИЧНЫЕ ИГРЫ

Рис.

В полученных результатах больше вопросов, чем ответов.

Ситуации (1,1) и (0,0) означают одновременный выбор игроками

первых или соответственно вторых стратегий, т. е. определенную до-

говоренность о совместных действиях.

Однако в данном случае есть еще одна ситуация равновесия, со-

стоящая в выборе игроками вполне определенных смешанных стра-

тегий. В ней оба игрока получают одинаковые выигрыши, правда,

меньшие тех, которые давали две другие равновесные ситуации.

Какой же из этих трех ситуаций равновесия следует отдать пред-

почтение? Какую выбрать игрокам?

Если бы игроки договорились выбрать одновременно, скажем, пе-

рвую чистую стратегию, причем игрок А за получение большего вы-

игрыша, чем игрок В, заплатил бы ему 1/2, то выигрыш каждым

полутора единиц можно было бы считать и выгодным, и справед-

ливым. Однако в рамках теории бескоалиционных игр такого рода

дележи не рассматриваются.

Вполне ясно, что для

выбора

каждым из игроков своей линии

поведения (напомним, что подобная ситуация может повторяться и

повторяется многократно) необходимы либо расширение возможно-

стей, имеющихся у игроков, либо иные, измененные критерии.

19.4.4. Студент - преподаватель

Наконец, обратимся к последнему из приведенных выше примеров

биматричных

игр — студент - преподаватель. Впечатления у каж-

388

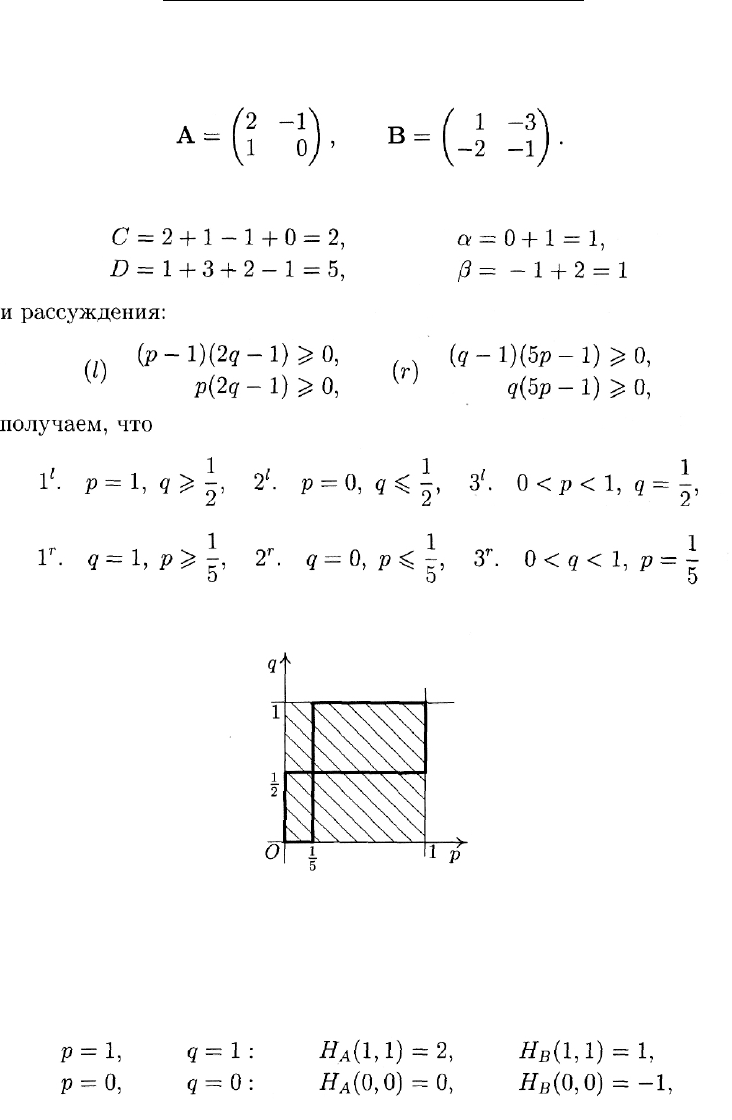
19.4. ПОИСК РАВНОВЕСНЫХ СИТУАЦИЙ

дого из них относительно результатов общения в матричном виде

выглядят следующим образом:

Проводя необходимые вычисления:

(рис. 7).

Рис. 7

Число точек пересечения у зигзагов (равновесных ситуаций) рав-

но трем.

Две из них отвечают чистым стратегиям игроков:

389

ГЛАВА 19. БИМАТРИЧНЫЕ ИГРЫ

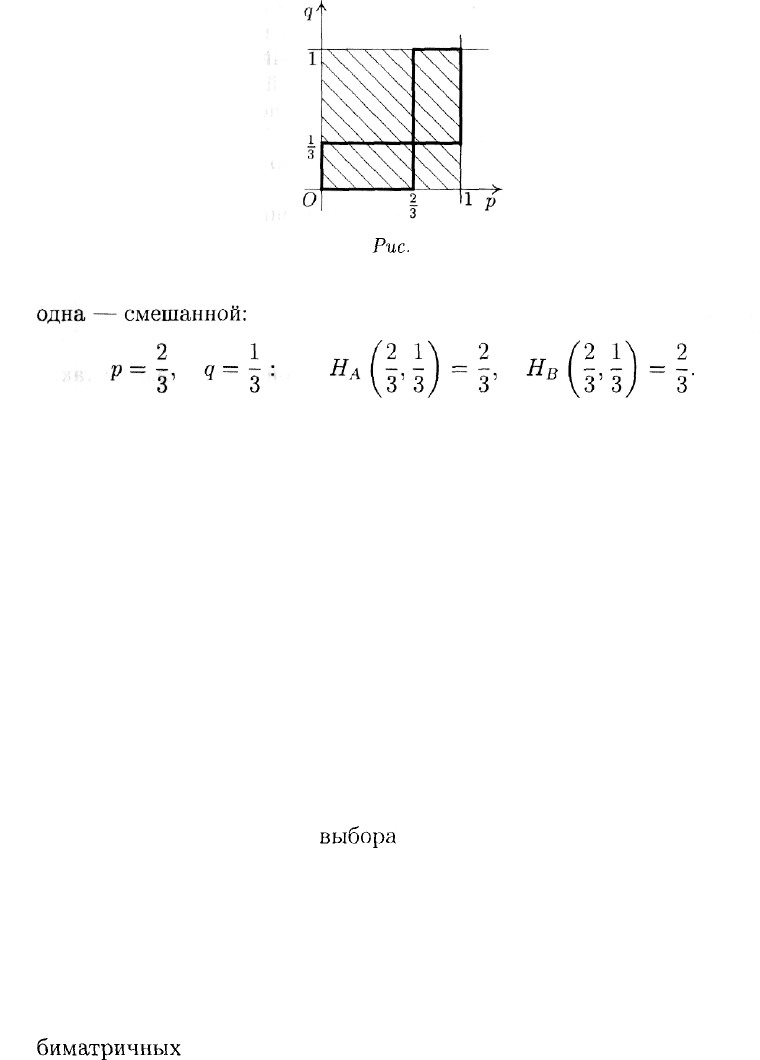
одна — смешанной:

В данной задаче в отличие от предыдущей все довольно ясно:

наилучшим является выбор каждым из игроков первой чистой стра-

тегии — хорошо подготовиться к зачету и поставить зачет.

Как нетрудно заметить, тем самым в этой

задаче

реализуется

весьма редкая возможность, когда функции выигрыша каждого из

игроков достигают своих максимумов одновременно.

Выгодность такой ситуации совершенно ясна. Ее устойчивость

также вполне очевидна: любое отклонение от ситуации (1,1) одного

из игроков или обоих игроков может привести разве что к уменьше-

нию их выигрышей.

19.5. Некоторые итоги

На анализе

полученных

результатов стоит остановиться чуть под-

робнее.

Из приведенных примеров видно, что числа С и D могут быть

как положительными, так и отрицательными. Они могут, в частно-

сти, даже обращаться в нуль.

Рассмотрим, однако, наиболее интересный в приложениях слу-

чай, когда ни С ни D нулю не равны, т. е.

Тогда, как нетрудно видеть, точка равновесия определяется парой

Эти формулы являются весьма примечательными: в равновесной

ситуации выбор игрока А полностью определяется элементами пла-

тежной матрицы игрока В,